约束陀螺柔性体执行机构优化配置和主动振动控制

贾世元，贾英宏，徐世杰，卢 山，侯月阳，王奉文

(1. 北京航空航天大学宇航学院，北京 100191；2. 上海航天控制技术研究所上海市空间智能控制技术重点实验室，上海 201109)

约束陀螺柔性体执行机构优化配置和主动振动控制

贾世元1，贾英宏1，徐世杰1，卢 山2，侯月阳2，王奉文2

(1. 北京航空航天大学宇航学院，北京 100191；2. 上海航天控制技术研究所上海市空间智能控制技术重点实验室，上海 201109)

研究了约束陀螺柔性体上执行机构的优化配置和主动振动控制，通过对带有变速控制力矩陀螺的单陀螺柔性体的模型简化，得到了线性化的约束陀螺柔性体的动力学模型。提出一种约束陀螺柔性体执行机构优化配置的新方法，该方法直接基于振动响应和振动能量对陀螺执行机构进行配置。优化配置的目标函数为线性二次型最优控制的最优值。将优化配置问题转化为整数组合优化问题，使用遗传算法(GAs)求解给定数目执行机构优化配置的组合问题。研究了执行机构在不同安装方向下的优化配置情况，优化配置的构型用于陀螺柔性体的主动振动控制。数值仿真校验了优化配置方法及结果的可行性和有效性。

约束陀螺柔性体；优化配置；遗传算法；振动抑制

0 引 言

随着空间任务的日益复杂，航天器的结构也日趋复杂，其中大型化、低密度和柔性化成为航天结构的一个重要发展趋势，为了降低发射成本和太空作业的需要，大型空间结构，如大型太阳帆板，大型天线和空间柔性机械臂等常常采用轻质材料制造。大型柔性结构通常具有大的挠性和较小的自身阻尼，而太空环境中几乎无外界阻尼。当大型复杂航天器在实现快速机动或受到外界干扰时，柔性结构会产生振动，振动将会严重影响元器件的工作，导致性能下降而失效[1]；另外，长期的振动也会引起结构的疲劳破坏。因此，以刚体为假设前提的被动振动控制不再适用于柔性复杂航天器的控制。

针对柔性航天器的振动抑制问题，许多学者采用不同的控制方法降低柔性结构的振动抑制[2-4]。为了实现大型空间柔性结构的主动振动抑制，大量文献讨论了在空间柔性结构上粘贴智能结构，如文献[5]基于欧拉-伯努利梁的有限元模型使用不同的控制策略研究了梁结构的主动振动控制。Ning[6]优化了压电片的数目和位置用来实现柔性结构的主动振动抑制。邱志成[7]针对挠性板结构的振动控制问题，给出了一种压电敏感器和驱动器同位配置的优化方法。Kim等[8]和Kumar等[9]讨论了柔性板上压电执行机构的分布问题。林西强等[10]将压电片用于层合板的振动控制。利用压电材料做成的执行机构/传感器能够适用于一般柔性结构的振动抑制，但是压电材料作为执行机构在大型空间柔性结构中的应用存在一定的问题，其最大缺点是压电执行机构提供的驱动力小。为了提供大型结构主动振动控制所需要的驱动能量，不得不增加执行机构的数目。执行机构的增加会给控制器的设计带来难度，而且计算量也会增加，这会对控制的实时性产生影响。

继而，D’Eleuterio 和 Hughes提出了陀螺柔性体理论[11-13]，陀螺柔性体是指具有连续储存角动量的柔性体，角动量装置可以直接产生控制力矩用于柔性结构的振动抑制。Damaren和D’Eleuterio[14-15]又进一步讨论了陀螺柔性体的能观性和能控性，他们认为能观性和能控性可以实现角动量的配置。但是在实际应用中不可能实现连续配置的角动量装置，角动量装置的配置必定是离散的，逐点配置的。因此，将配置有离散角动量装置的柔性体定义为陀螺柔性体。Aubrun 等[16]提出了陀螺阻尼器的概念，该阻尼器包含一个单框架控制力矩陀螺和一个角速度传感器。Shi等[17]也研究了类似的陀螺阻尼器用来实现悬臂梁的主动振动抑制。要实现角动量装置对柔性体的主动振动抑制，需要考虑角动量执行机构的优化配置，也就是将执行机构配置在柔性结构的什么位置能够具有较好的振动抑制效果。

陀螺执行机构优化配置的相关研究还比较少，Hu等[18]基于能观性和能控性指标对执行机构在柔性结构上的配置进行了讨论，但是通过该指标进行配置得到的构型在振动抑制中并不一定具有好的效果。另外，他们的研究只是针对单个执行机构在不同位置上的配置，没有讨论多个执行机构如何配置的问题。Chee和Damaren[19]研究了控制力矩陀螺在大型柔性结构上的分布，但是他们的研究主要在于控制力矩陀螺角动量的分布，而不是控制力矩陀螺位置的优化。Jia等[20]基于能观能控性指标研究了不同数目陀螺柔性体执行机构的优化配置问题，但是他们的研究中没有考虑执行机构安装方向的优化问题。本文研究了陀螺执行机构在柔性板上的配置问题，不同于以往的能观能控性指标，本文提出了基于线性二次型指标的陀螺执行机构优化配置方法，并将多个离散执行机构的配置问题转化为整数优化问题，利用遗传算法求解优化配置问题。并对执行机构在不同安装方向下的优化配置问题进行了讨论。数值仿真表明,通过线性二次型指标得到的优化配置构型能够较好地抑制柔性结构的振动。

1 约束陀螺柔性体的控制

1.1 约束陀螺柔性体的状态空间方程

文献[21]推导了具有离散变速控制力矩陀螺的单陀螺柔性体的动力学方程，文献[18]将该动力学方程化简为带有离散控制力矩陀螺的约束陀螺柔性体的动力学方程。该研究以约束陀螺柔性板为基本构型，如图1所示。约束柔性板上具有n个控制力矩陀螺，在板的约束端建立其体坐标系Fb，每个控制力矩陀螺固定一个框架坐标系，框架坐标系的中心在其质心上，并假设陀螺框架质心和转子的质心与整个陀螺的质心重合，第i个控制力矩陀螺的质心用Qgi表示。

图1(b)给出了第i个控制力矩陀螺的框架坐标系，其中xgi为单位向量沿框架速度方向；ygi为单位向量沿转子自旋轴方向；zgi通过右手法则确定。每个控制力矩陀螺具有给定的初始安装方向。假设在初始安装方向下，框架坐标系用Fgi0来表示，其组成向量为xgi0，ygi0和zgi0，其中xgi0与向量xgi的方向相同，ygi0为框架轴零初始条件下的转子自旋轴方向，zgi0=xgi0×ygi0。

忽略高阶小量并设约束板本体的速度和角速度为零，约束陀螺柔性板的动力学方程可以通过文献[21]中的式(7)得到

(1)

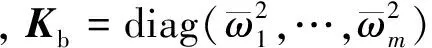
(2)

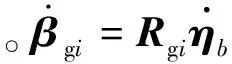
(3)

则约束陀螺柔性板的动力学方程可以简化为：

(4)

其中,

(5)

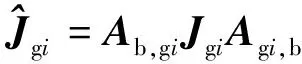
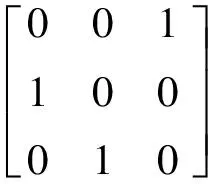
(6)

(7)

将该方程写成状态方程的形式

(8)

系统输出为柔性板的弹性位移

Y=CX

(9)

1.2 最优控制问题

基于状态空间模型，线性二次型最优控制可以应用到该系统中。对于给定的约束陀螺柔性体，线性二次型最优控制的性能指标如下：

(10)

式中:R和Q分别为正定对称阵和半正定对称阵。较大的Q值表明需要控制具有更大的振动抑制能力，式(10)中的第二项解释了控制系统的控制能力。系统最优控制律如下：

u=-PcX

(11)

其中，Pc=R-1BTS为控制增益，S为如下代数黎卡提方程的解

ATS+SA-SBR-1BTS+CTQC=0

(12)

2 优化配置问题

本文研究的目的是实现控制力矩陀螺执行机构的优化配置，并对约束陀螺柔性板进行振动抑制控制。目标函数选为式(10)中线性二次型最优控制的最优值，该最优值可以表示成如下形式：

(13)

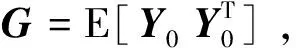
(14)

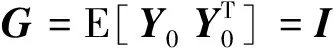
Jopt(x)=tr[S(x)]

(15)

目标函数的值表示了振动抑制快慢和控制量的权重之和。

执行机构的优化配置属于组合问题，遗传算法在求解组合问题中具有广泛的应用[22]，因此本文运用遗传算法对控制力矩陀螺执行机构进行优化配置。配置目标是确定n执行机构的位置使得目标函数值Jopt(xi)最小，优化配置是在线性二次型的基础上实现的。将离散的执行机构优化配置问题转化为整数优化的问题，使用遗传算法求解整数优化问题。遗传算法是随机搜索算法，该算法借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传、突变、自然选择以及杂交等。遗传算法通常情况下选用二进制字符串对变量进行编码，编码后的字符串对应于生物进化中的染色体，每个变量即为染色体上的一个基因。在进化过程中整数编码比二进制编码具有更快的进化速度，因此本文采用整数编码对执行机构进行优化配置。将执行机构的位置编码成一个整数字符串，字符串上第i个基因表示第i个执行机构的位置。个体的评价是通过适应度函数实现的，适应度函数对应于优化配置中的目标函数，种群的重组也是根据适应度函数进行的。新的代数是通过父代的选择交叉变异得到的。尽管遗传算法是随机搜索算法，但是遗传算法能够根据现有的知识探索得到具有好的适应度的新一代个体。遗传算法的进化流程如图2所示。

在应用遗传算法对执行机构做优化配置时需要对遗传算法做如下修正：

1)遗传算法的初始种群是随机产生的，当所有的执行机构都具有相同的初始安装方向时，染色体的长度与约束板上执行机构的数目相同。当执行机构具有不同的初始安装方向时，染色体的长度是执行机构数目的两倍，其中前n个基因表示n个执行机构的安装位置，后n个基因表示执行机构的初始安装方向。

2)对于所有执行机构具有相同初始安装方向的情况，染色体上每个基因的边界为[1,nnode]，其中nnode为柔性板上有限元节点的数目。对于执行机构具有不同初始安装方向的情况，染色体前n个基因的边界设为[1,nnode]，后n个基因的边界设为[0, 1]，其中0表示陀螺的初始安装方向与式(3)中的方向相同，即陀螺框架轴初始方向xgi0沿柔性板本体坐标系xb的负方向，陀螺转子初始自旋方向ygi0沿柔性板本体坐标系zb的正向，zgi0沿柔性板本体坐标系yb的正向。1表示陀螺的初始安装方向与式(6)中的方向相同，即陀螺框架轴初始方向xgi0沿柔性板本体坐标系yb的正向，陀螺转子初始自旋方向ygi0沿柔性板本体坐标系zb的正向，zgi0沿柔性板本体坐标系xb的正向。

3)为避免执行机构在相同位置的重复配置，需要在遗传算法中添加约束，当某个染色体的前n个基因中有任意两个基因的值相同，则该染色体表示的个体无效，需要重新生成个体，直到每个个体均为有效个体后再对种群进行下一代的进化。

3 结果和讨论

本部分给出了约束陀螺柔性板执行机构优化配置的结果及讨论。将约束板离散成20×12个板元素，板的有限元中共包含273个节点，从固定端的一个角上开始对节点进行编号，将该节点编号为1。固定端上共有13个节点，分别为[1, 22, 43, 64, 85, 106, 127, 148, 169, 190, 211, 232, 253]，其余节点按照从固定端到自由端逐渐增大的原则进行编号。执行机构的位置通过板的节点来表示，所有的节点均为执行机构和候选位置。执行机构的数目假设为固定值6，所有的陀螺转子假设均具有相同的角动量hi=2 Nm/s，角动量的初始方向均沿zb轴如图3所示，板和陀螺的质量特性和几何数据如表1所示，为了更好地观察执行机构对柔性板的主动振动抑制效果，优化配置及控制中忽略板的自身阻尼。选择柔性板的前六阶模态(如图4所示)对执行机构进行优化配置，约束柔性板的前六阶频率分别为0.03583505 Hz, 0.1308988 Hz, 0.2223560 Hz, 0.4341273 Hz, 0.6114872 Hz和0.6870883 Hz。

本文讨论了三种不同案例的执行机构初始安装方向。“案例1”表示所有的执行机构的初始安装方向均与式(3)中的方向相同，“案例2”表示所有执行机构的初始安装方向均与式(6)中的方向相同，“案例3”表示执行机构的初始安装方向可以为混合安装方式，即每个执行机构的初始安装方向既可以与式(3)中的方向相同也可以与式(6)中的方向相同。

遗传算法用于6个执行机构优化配置时参数设置如下：种群数目为100；交叉概率为0.85；变异概率为0.02；最大进化代数为5000。不同案例下的遗传算法收敛特性如图5所示。从图5可以看出,案例2中的目标函数最小值比案例1和案例3中的目标函数最小值要大，案例3具有最小的适应度函数值。案例1中执行机构的优化配置位置为[18, 11, 263, 271, 270, 19]；案例2中执行机构优化配置位置为[7, 8, 259, 260, 13, 265]；案例3中执行机构优化配置的位置和方向为[18, 19, 271, 20, 272, 270, 0, 0, 0, 1, 1, 0]，通过方向参数可以看出安装在节点18,19,271和270上的执行机构初始安装方向与式(3)中的方向相同，而安装在节点20和272上的执行机构初始安装方向与式(6)中的方向相同。优化结果表明,执行机构主要配置在板的两侧和角上，主要是由于这些位置具有较大的模态斜率，执行机构在优化位置上的配置能够更好地抑制约束陀螺柔性板的振动。

根据执行机构优化配置的结果，讨论陀螺执行机构对柔性板的振动抑制情况。模态坐标初值设为[0.5, -0.4, -0.2, -0.2, 0.1, -0.1]，线性二次型权重因子为Q=1,R=1，不同案例下的前六阶模态坐标的响应如图6～8所示。从图6～8可以看出,案例1和案例3对模态的振动抑制效果较案例2好，案例1和案例3相比，其二阶模态的收敛速度比案例3中的模态收敛速度慢，会影响整个柔性板的振动抑制效果，从总体效果来看，案例3的各阶模态都能够以相对较快的速度收敛，这表明陀螺执行机构混合安装方式对柔性板的振动抑制效果比单一方向的安装方式要好。

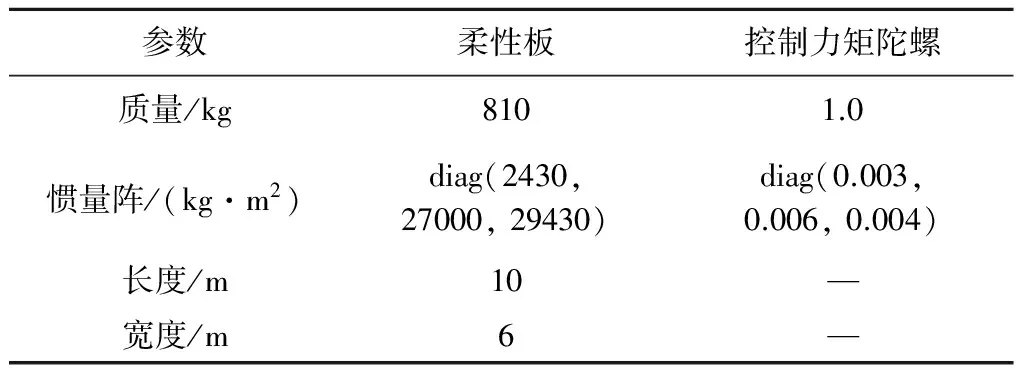
参数柔性板控制力矩陀螺质量/kg8101．0惯量阵/(kg·m2)diag(2430，27000，29430)diag(0．003，0．006，0．004)长度/m10—宽度/m6—

不同案例下的陀螺框架速率如图9～11所示。从图9～11可以看出，案例3的陀螺框架速率比案例1和案例2的陀螺框架速率小。因此，案例3的能量消耗比案例1和案例2的能量消耗小，其中案例2的能量消耗最大。这表明混合安装的执行机构能够以相对较小的能量实现较快的振动抑制。能量消耗的多少与执行机构的安装位置和安装方向密切相关的。案例3中执行机构有两种安装方向，能够同时提供xb和yb方向的力矩，该力矩能够实现柔性结构的弯曲和扭转振动抑制，而执行机构安装在优化位置上能够使陀螺力矩最大效果的用于振动抑制，因此案例3在各阶模态的振动抑制效果较好。而案例1中执行机构在单一安装方向下只能产生yb方向的力矩，该力矩能够较好地抑制柔性结构的弯曲振动，而柔性结构的扭转振动需要通过陀螺与柔性结构的耦合实现。同样情况案例2中的执行机构在其安装方向下只能产生xb方向的力矩，该方向的力矩可以直接用于柔性结构的扭转振动抑制，柔性体的弯曲振动抑制同样需要陀螺与柔性结构的耦合实现。案例1和2的执行机构的配置位置能够使一种方向的振动得到抑制的同时使另一种方向的振动得到有效的抑制。由于柔性结构的振动主要为弯曲振动，案例1产生的力矩能够直接用于弯曲振动抑制，控制输入相比案例2更有效，因此案例1的能量消耗比案例2的能量消耗小。

4 结 论

本文研究了约束陀螺柔性体的执行机构优化配置和主动振动控制问题。将动力学模型转换为状态空间的形式，基于振动抑制的效果提出了约束陀螺柔性体执行机构优化配置的新方法。以线性二次型指标最优控制的最优值为目标函数，使用遗传算法对给定数目的陀螺执行机构进行了优化配置，讨论了陀螺执行机构在不同安装方式下的配置，从配置结果可以看出，执行机构主要安装在约束柔性板的两侧和角上。通过性能指标的大小和振动抑制的效果来看，陀螺执行机构初始方向混合安装情况要比单一方向的安装效果好，线性二次型最优控制下的混合执行机构安装方式能够实现较小陀螺输入下的有效振动抑制。

[1] 刘天雄，林益明，王明宇，等．航天器振动控制进展 [J]. 宇航学报, 2008, 29(1):1-12. [Liu Tian-xiong, Lin Yi-ming，Wang Ming-yu,et al．Review of spacecraft vibration control technology [J]. Journal of Astronautics, 2008, 29(1):1-12.]

[2] 姚雨晗，周军，刘莹莹，等．基于输入成型法的空间站变构型过程挠性振动抑制策略 [J]. 宇航学报, 2013, 34(5):665-670. [Yao Yu-han, Zhou Jun, Liu Ying-ying,et al.Research on flexible vibration suppression strategy for variable configuration space station based on input shaping technique [J]. Journal of Astronautics, 2013, 34(5):665-670.]

[3] 蔡鹏，王庆超．基于自适应模糊观测器的挠性航天器主动振动抑制方法研究 [J]. 宇航学报, 2009, 30(3):890-894. [Cai Peng, Wang Qing-chao.Active vibration control for flexible spacecraft using an adaptive fuzzy observer [J]. Journal of Astronautics, 2009, 30(3):890-894.]

[4] 王晓磊，吴宏鑫．挠性航天器振动抑制的自适应方法及实验研究 [J]. 宇航学报, 2005, 30(3):275-281. [Wang Xiao-lei, Wu Hong-xin．Active control scheme and experiment for vibration suppression of flexible spacecraft [J]. Journal of Astronautics, 2005, 30(3):275-281.]

[5] Balamurugan V, Narayanan S. Active vibration control of piezolaminated smart beams [J]. Defence Science Journal, 2001, 51(2): 103-14.

[6] Ning H H. Optimal number and placements of piezoelectric patch actuators in structural active vibration control [J]. Engineering Computations,2004,21(6): 651-65.

[7] 邱志成. 挠性板振动抑制的敏感器与驱动器优化配置[J]. 宇航学报, 2002, 23(4):30-36. [Qiu Zhi-cheng. Optimal placement of sensors and actuators for flexible plate of vibration suppression [J]. Journal of Astronatics, 2002, 23(4):30-36.]

[8] Kim T W, Kim J H. Optimal distribution of an active layer for transient vibration control of a flexible plate [J]. Smart Materials and Structures,2005, 14(5): 904-16.

[9] Kumar K R, Narayanan S. The optimal location of piezoelectric actuators and sensors for vibration control of plates [J]. Smart Materials and Structures,2007, 16(6): 2680-2691.

[10] 林西强, 任钧国. 含压电片层合板的振动控制 [J]. 宇航学报, 2000, 21(1):91-95. [Lin Xi-qiang, Ren Jun-guo. Vibration control of lam inate plate containing piezoelectric patches [J]. Journal of Astronatics, 2000, 21(1):91-95.]

[11] D′Eleuteriot G M T, Hughes P C. Dynamics of gyroelastic continua [J].Journal of Applied Mechanics, 1984, 51(2): 415-422.

[12] D′Eleuteriot G M T, Hughes P C. Dynamics of gyroeiastic spacecraft [J].Journal of Guidance, Control, and Dynamics, 1987, 10(4): 401-405.

[13] D′Eleuteriot G M T. Dynamics of gyroelastic vehicles[D]. Toronto:University of Toronto,1986.

[14] Damaren C J, D′Eleuteriot G M T. Controllability and observability of gyroelastic vehicles [J]. Journal of Guidance, Control, and Dynamics, 1991, 14(5): 886-894.

[15] Damaren C J, D′Eleuteriot G M T. Optimal control of large space structures using distributed gyricity [J]. Journal of Guidance, Control, and Dynamics, 1989, 12(5): 723-731.

[16] Aubrun J N, Margulies G. Gyrodampers for large space structures [R]. Palo Alto, United States: Lockheed Aircraft Corp, Feb. 1979.

[17] Shi J F, Damaren C J. Control law for active structural damping using a control moment gyro [J]. Journal of Guidance, Control, and Dynamics, 2005, 28(3): 550-553.

[18] Hu Q, Zhang J R. Placement optimization of actuators and sensors for gyroelastic body [J]. Advances in Mechanical Engineering, 2015, 7(3): 1-15.

[19] Chee S A, Damaren C J. Optimal gyricity distribution for space structure vibration control [J]. Journal of Guidance, Control, and Dynamics, 2015, 38(7): 1218-1228.

[20] Jia S Y, Jia Y H, Xu S J, et al. Optimal placement of sensors and actuators for gyroelastic body using genetic algorithms [J]. AIAA Journal, 2016, 54(8): 2472-2488.

[21] Hu Q, Jia Y H, Xu S J. Recursive dynamics algorithm for multibody systems with variable-speed control moment gyroscopes [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1388-1398.

[22] Han J H, Lee I. Optimal placement of piezoelectric sensors and actuators for vibration control of a composite plate using genetic algorithms [J]. Smart Materials and Structures, 1999, 8(2): 257-267.

ActiveVibrationControlofConstrainedGyroelasticBodywithOptimalPlacementofActuators

JIA Shi-yuan1, JIA Ying-hong1, XU Shi-jie1, LU Shan2, HOU Yue-yang2, WANG Feng-wen2

(1. School of Astronautics, Beihang University, Beijing 100191, China; 2. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai Aerospace Control Technology Institute, Shanghai 201109, China)

The optimal placement of the actuators and the active vibration suppression of the constrained gyroelastic body is studied. By simplifying the model of a single gyroelastic body with variable-speed control moment gyros, the linearized dynamic model of the constrained gyroelastic body is obtained. A new method is proposed for the optimal placement of the actuators. This method is directly based on the vibration responses and vibration energy to determine the optimal placement of the actuators. The objective function is chosen as the optimal value of the linear quadratic regulator control. The optimal placement of the actuators is formulated in the frame of the combinatorial integer optimization problem. The genetic algorithms (GAs) are used to solve the combination problem of the constrained gyroelastic body with a fixed number of actuators. The optimal placement of the actuators with different installation directions is studied. The optimized configurations are used to realize the active vibration suppression. The effectiveness and feasibility of the optimized results by the proposed method are validated by the numerical simulations.

Constrained gyroelastic body; Optimal placement; Genetic algorithm; Vibration suppression

2017- 03- 06;

2017- 09- 20

国家自然科学基金(11272027)；上海市自然科学基金(16ZR1415600), 上海市科技人才计划(17XD1420700)

V41

A

1000-1328(2017)12- 1297- 10

10.3873/j.issn.1000- 1328.2017.12.006

贾世元(1988-)，男，博士生，主要从事多体动力学与控制方面的研究。

通信地址：北京市海淀区学院路37号(100191)

电话：(010)82339751

E-mail:jiashi.yuan@163.com