一种飞轮微振动特性分级方法
2018-01-04罗睿智张激扬樊亚洪冯洪伟
罗睿智,张激扬,樊亚洪,冯洪伟,姚 锐
(1.北京控制工程研究所,北京100094;2.中国空间技术研究院,北京100094)
一种飞轮微振动特性分级方法
罗睿智1,2,张激扬1,2,樊亚洪1,冯洪伟1,姚 锐1
(1.北京控制工程研究所,北京100094;2.中国空间技术研究院,北京100094)
针对飞轮在工作中伴随输出的宽频微幅振动,运用分位数统计方法建立了飞轮微振动幅值的评估方法和分级标准。首先,基于飞轮的工作转速范围和航天器舱板挠性对微振动的衰减作用,对飞轮微振动瀑布图进行二维加权;其次,利用经验分布对飞轮在缓慢升速过程中的微振动瀑布图的振幅进行下分位数统计,得到任意概率下的飞轮微振动瀑布图;然后,对瀑布图在频率和转速轴进行逐步降维,统计微振动在频率轴和转速轴的振动均方根值,得到了飞轮从三维立体到单个点的多种分级方法。最后,对25个50 Nms飞轮的微振动瀑布图数据进行相应的统计分析,首次建立了飞轮从三维微振动瀑布图到数据点的一系列微振动分级标准(包括Ⅰ至Ⅵ级)。为超静飞轮的研制和筛选奠定了初步的理论和工程基础。
飞轮;微振动;分位数;分级;经验分布
0 引 言
飞轮是卫星等航天器的常用惯性姿态执行机构,它主要包括:轮体组件、电机组件、轴承组件和壳体组件[1](其结构如图1所示)。其中,轮体、电机转子和轴承组件的部分零件等构成飞轮旋转体,通过电机驱动旋转体高速转动来产生并储存角动量,通过变速改变角动量的大小输出控制力矩,实现对航天器的姿态机动或稳定。可见旋转体是动量轮的核心部件,但是其高速旋转过程中伴随输出的宽频微振动也是影响卫星姿态稳定和精确指向的最大干扰源[2-3]。随着用户对卫星功能和性能需求的提高,这种干扰日益突显出来,制约着遥感卫星、激光通讯卫星等航天器的姿态稳定度的进一步提升,因此针对飞轮微振动的动力学特性研究和抑制[4-5]成为惯性执行机构技术发展的重要方向。
目前针对高速转子的动力学特性分析和振动抑制方法研究得较多,而对飞轮的微振动进行评估的文献较少,未见针对飞轮的微振动测试结果的统计分析和分级研究的文献,飞轮微振动性能的评价体系尚未建立,可是这些正是飞轮研制以及航天器设计和应用所关心的关键问题。相反,在传统机械行业针对压缩机[6]、柴油机[7]和泵[8]等设备的振动标准早已建立且比较完善,它们采用振动烈度、应力和加速度等参数对设备产生的振动进行评估和分级。美国海军规范了气、液、固三态介质的振动和噪声的评估基准参考量[9],并给出了振动和噪声的分级计算公式。近年随着我国飞轮产品量产,急需建立飞轮微振动评价和分级的相关标准。最简便有效的方法是对已有的飞轮微振动数据进行统计分级,并以此作为后续飞轮微振动性能评价与定级的参考标准。鉴于惯性执行机构的微振动力和力矩是通过其基座外传至航天器舱板上,进而影响到航天器的姿态稳定性,影响到附近的对微振动敏感的载荷设备的性能发挥,因此微振动力和力矩最适合作为飞轮等惯性执行机构的微振动评价物理量。限于篇幅,本文仅以振动力为例进行统计分析。
鉴于50 Nms飞轮产品的质量严格受控,工艺过程固化。各台飞轮产品的零件、工艺等众多过程参数的一致性较好,而每台单机产品的微振动特性是由这些因素综合作用的结果。因此可以预见飞轮产品的微振动特性相对稳定,所积累的大量的飞轮微振动数据具有一定的统计规律性。
在对飞轮进行微振动测试时,飞轮通过转接工装固定于Kistler的多分量测力台上(如图2所示),利用该测力台测试飞轮在运行的过程中其安装界面输出的三方向振动力和力矩,所有飞轮产品的微振动测试状态一致,满足统计条件,因此通过对微振动力和力矩测试数据的统计分析,即可得到飞轮产品的微振动特性。本文将对25个50Nms飞轮的微振动瀑布图测试结果在全转速中、低频段内多个概率等级下的分布情况进行下分位数统计,并以此为依据建立飞轮产品的微振动分级标准。期望为后续的高稳定度飞轮设计和筛选提供初步的参考依据。
1 飞轮微振动瀑布图的插值与加权处理
在对飞轮产品进行微振动测试的过程中,由于微振动测试设备对低转速脉冲计数的误差,使得所得到的瀑布图不均匀,转速越低,这种转速误差越明显;同时由于各个型号的要求不同,在各次微振动测试中,设置的频率分辨率也各不相同。这就导致了各个飞轮产品的微振动瀑布图在“转速-频率”二维平面上的取点各不相同,因此需要对这些瀑布图进行规整,即在一些固定的“转速-频率”点对所测得的瀑布图进行二维插值,最终得到各飞轮在统一网格上的微振动瀑布图。
对于二元函数w=g(f,s),其自变量f表示频率,s表示转速,在平面矩形格点上的函数值wij=g(fi,sj),i=0,1,2,…n;j=0,1,2,…m,通过微振动瀑布图测试获得。则在该矩形网格内任意点(f,s)的二元双线性插值(也称Lagrange插值)为:
(1)
式中:
f∈(fp,fp+1),p∈{0,1,2,…,n-1}s∈(sq,sq+1),q∈{0,1,2…m-1}
由于振动瀑布图中的各点间距比较密集,采用双线性插值不会导致较大精度损失。
鉴于航天器的舱板具有一定的柔性,对飞轮的高频微振动具有一定的衰减作用[10],因此飞轮的低频微振动对航天器影响更大,在此不妨假设舱板具有二阶衰减率(实际的衰减率需要根据舱板的具体情况而定)。另一方面,鉴于飞轮运行在其工作转速范围之内,该转速范围内的微振动才会对卫星等航天器的姿态稳定性造成一定的影响。可是各个型号对各个飞轮产品的工作转速范围要求都不尽相同,且同一个飞轮运行在各个转速的频度也不一致。因此,难以确定飞轮工作转速服从某种统计分布,所以本文不妨将工作转速范围内的微振动进行平均加权,据此构造权函数:
β(f,s)=
(2)
式中:su表示工作转速的上限,sd表示工作转速的下限,fc表示航天器对飞轮微振动敏感的截止频率,ζ表示阻尼比。因此飞轮在微振动瀑布图中任意点的微振动加权后的幅值为:
v(f,s)=β(f,s)α(f,s)
(3)
针对某型号用飞轮工作在1000~4000 r/min,星体对飞轮微振动敏感的截止频率fc暂取为200 Hz,阻尼比ζ暂取为0.707,则该权函数如图3所示。
2 飞轮的微振动特性分级方法研究
统计作为一种数学工具,已被广泛应用于科学研究和工程技术中,极大地促进了科技发展。鉴于飞轮的微振动特性受到零件参数、装配间隙、轴承预紧力[11]等众多因素的影响,很难从理论上证明其微振动一定满足某种概率分布,更难保证微振动瀑布图在“转速-频率”平面内的各网格点的振幅都满足统一的概率分布,故本文拟采用经验分布[12-17]对微振动瀑布图进行分位数统计。
设飞轮微振动瀑布图在同一网格点上的幅值V为实数随机变量,微振动幅值的分布函数为:F(v)=Prob(V≤v),设其经验分布函数为:
(4)
则对任意实数τ(0<τ<1)有:
(5)
式(5)为随机变量V的τ分位数,即:
1)对样本进行从小到大排序{v1,v2,…,vn};
2)计算Fk=(k-0.5)/n,k∈{1,2,…,n};样本及其对应的分位数如表1所示。

表1 样本的分位数对照表Table 1 Comparison Table of sample quantile
显然,由此计算的n个分位数呈阶梯型,为了提高其精度,需对其进行一阶平滑,即对该n个分位数之间的部分进行线性插值计算。
3)对Fk和Fk+1之间的分位数进行线性插值,如该分位数为Fkτ,其中k (6) 由式(6)可计算出任意概率的分位数。 为了实现对飞轮微振动的近似均匀分级,不妨以概率τ∈{0.2,0.4,0.6,0.8,0.95}作为其微振动分级概率,分级与分位数的对应关系如表2所示。 表2 飞轮产品的微振动特性分级表Table 2 Micro vibration characteristics rating of flywheel 由微振动测试得到飞轮产品的微振动瀑布图,通过对众多测试瀑布图中的各点进行分位数统计,计算各分级曲面,从而得到等级分布。 针对飞轮微振动的分级研究按照从微观到宏观,从复杂到简单的顺序逐级简化。形成飞轮的从三维立体到点的多个维度的分级标准。 将25个飞轮在从0到4600 r/min缓慢升速过程中其安装界面处输出的微振动瀑布图一一在规则的“频率-转速”网格点(fi,sj)处进行插值。其中: (fi,sj)= {(0.75f,50s)|f∈N,f≤533; s∈N,s≤92} 将规整后的所有飞轮的微振动幅值在各网格上进行分位数分级统计。既要便于直接和飞轮产品微振动瀑布图的测试结果进行对照,又需要考虑飞轮的工作转速范围及航天器舱板对微振动的衰减,因此对微振动瀑布图进行了未加权和加权两种条件下的分位数统计分析,统计结果对比如图3所示。 从图3可以看出,τ×100%的飞轮的微振动都位于该振动以下。其中,Ⅴ级飞轮的微振动瀑布图表示95%的飞轮的微振动不超过该瀑布图。超过该瀑布图的飞轮产品的微振动特性则属于Ⅵ级。鉴于篇幅限制,其余的振动力和振动力矩的分级标准不再一一列出(下同)。 由上述对飞轮微振动瀑布图的统计可知:1)飞轮在运行过程中所产生的微振动整体上会随着转速的升高而增加。2)对性能好的飞轮的微振动主要是工频振动;对于性能一般的飞轮的微振动除了随工频振动外,还主要存在介于120~220 Hz范围内的振动成分,但是经舱板减弱了该频段微振动的幅度。3)经过加权统计使得对航天器影响较大的微振动突显出来。 飞轮的微振动瀑布图分级是对产品微振动性能的细致刻画,不便于人们宏观简单地把握其特性。因此需要将这些瀑布图进行降维,包括:1)基于转速的振动功率谱分级;2)基于频率的振动功率谱分级;3)基于飞轮振动功率的分级。 考虑到飞轮的工作转速范围和航天器对微振动的衰减作用,有必要在对瀑布图降维之前对各飞轮的微振动瀑布图中各点幅值进行加权处理。 飞轮是通过变速实现动量交换进行工作的,因此转速对于飞轮的微振动特性具有重要的评价作用。故本文首先统计飞轮在各个转速下的振动功率Ps(见式(7)),再将每个飞轮的Ps按照第2节的方法计算各分级标准。这对用户选择飞轮产品及其工作转速区间都具有重要参考价值。 (7) 各个飞轮的基于转速的微振动功率谱分级曲线如图5(a)所示。图5(a)是经过统计所有飞轮的基于转速的微振动功率分级得到的曲线,以此作为飞轮微振动在转速轴上的分级判据。图5(b)是各飞轮基于转速的功率谱,从图5(b)可以看出:不同的飞轮的微振动分布于不同的级别;同一个飞轮的微振动在不同转速分属于不同的级别。 由图5(a)可知,80%的飞轮的微振动功率谱曲线都比较集中,余下的20%的飞轮的功率谱曲线比较分散,这主要是因为某些飞轮在不同的转速出现振动幅值较大的频率成分。从图5(b)可以看出,不同的飞轮存在其最优的转速区间,因此可以结合需求,选择最优转速范围以减小其影响。 一般而言,航天器上的其它设备对扰振的敏感度和扰振频率直接相关。而飞轮是通过变速来进行工作的,故需考核飞轮在全转速范围内微振动功率Pf随频率f的分布情况: (8) 各个飞轮的基于频率的微振动功率谱分级曲线如图6所示。图6(a)是经过统计所有飞轮的基于频率的微振动功率得到的功率分级曲线。这在关注的0~400 Hz范围内建立起了飞轮微振动分级的判据。图6(b)是各个飞轮的振动功率。 由上述统计分析可知:1)除了工作转速内的工频外,其余振动主要集中于120~220 Hz范围内。2) 60%的飞轮的微振动在频率轴上振动幅值比较集中,可是剩余的40%的飞轮的微振动比较分散。3) 从图6(b)可以看出,12号飞轮在80 Hz处存在异常突跳,故在选用该飞轮前应仔细斟酌。 尽管利用统计方法从曲面、曲线的角度建立了飞轮的微振动分级判据,但仍不够直观,且同一个飞轮的微振动在不同转速和频段分属不同的级别,难以得到一个唯一的标准,为此对每个飞轮在全转速全频域内求振动功率,如下所示: (9) 飞轮的微振动功率进行分级如图7所示。由图7可知,大部分产品的微振动都位于0.95以下。超出0.95的5号飞轮的幅值偏离较大,因此该飞轮也需斟酌使用。该标准为飞轮产品的微振动定级提供了一个简单直观的分级判据。 通过对飞轮微振动瀑布图的分位数统计研究,初步得到了飞轮从三维微振动瀑布图到数据点的一系列简单有效的分级方法。并成功应用于某50 Nms飞轮的微振动瀑布图的分级统计,首次建立了该型飞轮的微振动定量分级标准。为飞轮微振动性能分级提供了判定依据,为超静飞轮的筛选和工作转速范围的选择提供了参考依据。 [1] Sathyan K, Gopinath K, Hsu H Y, et al. Development of a lubrication system for momentum wheels used in spacecrafts [J]. Tribology Letters, 2008, 32(2):99-107. [2] 刘天雄,范本尧,杨慧.卫星飞轮扰振控制技术研究[J].航天器工程, 2009,18(1):53-60. [Liu Tian-xiong, Fan Ben-yao, Yang Hui. Research on vibration disturbance control of momentum wheel [J]. Spacecraft Engineering, 2009, 18(1): 53-60.] [3] 庞世伟,杨雷,曲广吉.高精度航天器微振动建模与评估技术最近进展[J].强度与环境, 2007, 34(6):1-9. [Pang Shi-wei, Yang lei, Qu Guang-ji. New development of micro-vibration integrated modeling and assessment technology for high performance spacecraft [J]. Structure & Enviroment Engineering, 2007, 34(6):1-9.] [4] 张庆君,王光远,郑钢铁.光学遥感卫星微振动抑制方法及关键技术[J].宇航学报, 2015,36(2):125-132. [Zhang Qing-jun, Wang Guang-yuan, Zheng Gang-tie. Micro-vibration attenuation methods and key techniques for optical remote sensing satellite [J]. Journal of Astronautics, 2015, 36(2):125-132.] [5] 刘天雄,林益明,王明宇,等.航天器振动控制技术进展[J]. 宇航学报, 2008, 29(1): 1-12.[Liu Tian-xiong, Lin Yi-ming, Wang Ming-yu, et al. Review of the spacecraft vibration control technology[J]. Journal of Astronautics, 2008, 29(1): 1-12.] [6] JB/T 8541—2013.容积式压缩机机械振动分级[S]. [7] CB 3325—1987.船用柴油机轴系扭转振动分级[S]. [8] JB/T 8097—1999.泵的振动测量与评价方法[S]. [9] MIL-STD-1621A. Acoustical and vibrational standard reference quantities[S]. [10] 王光远,周东强,赵煜.遥感卫星在轨微振动测量数据分析[J].宇航学报, 2015,36(3):261-267. [Wang Guang-yuan, Zhou Dong- qiang, Zhao Yu. Data analysis of micro vibration on orbit measurement for remote sensing satellite [J]. Journal of Astronautics, 2015, 36(3):261-267.] [11] 王虹,卿涛,周刚,等.预载对飞轮用轴承组件振动特性的影响研究[J].空间控制技术与应用, 2015, 41(1):41-45. [Wang Hong, Qing Tao, Zhou Gang, et al. Effects of preload on the micro-vibration properties of bearing assemblies in flywheels [J]. Aerospace Control and Application, 2015, 41(1): 41-45.] [12] 关静.分位数回归理论及其应用[D].天津:天津大学, 2008. [Guan Jing. Theory and application of quantile regression [D]. Tianjin: Tianjin University, 2008.] [13] 管河山,王谦,唐德文. 基于分位数特征提取的时间序列模式分类[J].计算机工程, 2015, 41(3):167-171. [Guan He-shan, Wang Qian, Tang De-wen. Time sequence pattern classification based on quantile feature extraction [J]. Computer Engineering, 2015, 41(3):167-171.] [14] 程维虎.利用样本分位数的极值分布的参数估计[J].北京工业大学学报, 2002, 28(3):326-328. [Chen Wei-hu. Parameter estimation for extreme-value distribution based on thepi-th quantiles of samples [J]. Journal of Beijing Polytechnic University, 2002, 28(3): 326-328.] [15] 陈建宝,丁军军.分位数回归技术综述[J].统计与信息论坛, 2008, 23(3):89-96. [Chen Jian-bao, Ding Jun-jun. A review of technologies on quantile regression [J]. Statistics & Information Forum, 2008, 23(3):89-96.] [16] 徐志科,平根建.非参数方法估计分位数模型的研究综述[J].数学的实践与认识,2014, 44(1):151-157. [Xu Zhi-ke, Ping Gen-jian. The summary of nonparametric quantile estimation [J]. Mathematics in Practice and Theory, 2014, 44(1):151-157.] [17] 张建华,曾建潮.经验分布函数概率模型的分布估计算法[J].计算机工程与应用, 2011, 47(8):33-35. [Zhang Jian-hua, Zeng Jian-chao. Estimation of distribution algorithms using empirical distribution function as probability model [J]. Computer Engineering and Applications, 2011, 47(8):33-35.] AClassificationMethodofFlywheelMicro-VibrationCharacteristics LUO Rui-zhi1,2, ZHANG Ji-yang1,2, FAN Ya-hong1, FENG Hong-wei1,YAO Rui1 (1. Beijing Institute of Control Engineering, Beijing 100094, China; 2. China Academy of Space Technology, Beijing 100094, China) The evaluation method and classification standard are established from the quantile for the broadband micro-vibration that the flywheels output to the spacecraft such as satellite in their rotations. Firstly, two dimensional weights are performed to the micro-vibration waterfall combining with the working speed range of the flywheel and the damping of the flexible spacecraft plate. Secondly, the empirical probability distribution is used to calculate the quantile of the amplitude at each grid point of the micro-vibration waterfall in the slow speed increasing process. Thus the micro-vibration waterfall of the flywheel can be obtained at any probability. Thirdly, the dimensions are gradually reduced in frequency and speed dimensions. The root mean square values of the vibration in frequency axis and speed axis are respectively compiled by statistics. The multidimensional classification criteria of the flywheel are obtained. Finally, the statistics is performed based on the micro-vibration waterfall data from 25 flywheels whose angular momentum are 50 Nms. Some classification criteria for the flywheel are obtained from the 3D waterfalls to the data points. The foundation can be laid in the theory and engineering for the development and screening of the ultra quiet flywheel. Flywheel; Micro-vibration; Quantile; Rating; Empirical probability distribution 2017- 03- 22; 2017- 08- 28 V414.3+3 A 1000-1328(2017)12- 1324- 07 10.3873/j.issn.1000- 1328.2017.12.009 罗睿智(1982-),男,工程师,主要从事空间惯性执行机构的微振动控制技术方面的研究。 通信地址:北京市海淀区友谊路104号(100094) 电话:(010)68111209 E-mail: rzllrz@sina.cn

3 飞轮的微振动测试结果统计
3.1 飞轮微振动瀑布图的定级研究
3.2 基于转速的振动功率谱分级

3.3 基于频率的振动功率谱分级
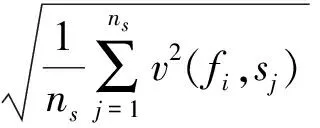
3.4 基于飞轮振动功率的分级

4 结 论
