UKF位姿估计的超静平台耦合模型参数辨识

张科备，王大轶，王有懿

(1.北京控制工程研究所，北京 100190；2. 北京空间飞行器总体设计部，北京 100190)

UKF位姿估计的超静平台耦合模型参数辨识

张科备1，王大轶2，王有懿1

(1.北京控制工程研究所，北京 100190；2. 北京空间飞行器总体设计部，北京 100190)

针对载荷无陀螺时辨识超静平台耦合动力学参数存在位姿确定问题，设计了一种基于Schur分解以及无迹卡尔曼滤波(UKF)的位姿确定及参数辨识方法。首先，建立加速度计和姿态敏感器组成的测量系统状态模型和观测模型，并给出测量系统的可观性分析。然后，给出基于UKF的载荷位姿确定方法；在UKF中引入姿态修正信息，从而提高载荷角速度估计精度，实现载荷广义位移、广义速度、广义加速度的准确估计。通过Schur分解实现超静平台动力学模型解耦及辨识模型中动力学参数显式表达。以滤波器估计载荷位姿信息为依据，采用最小二乘法辨识动力学参数。仿真结果表明UKF能够准确估计载荷角速度以及超静平台支杆刚度系数，辨识误差优于百分之一。

Stewart超静平台；位姿确定；无迹卡尔曼滤波(UKF) ；参数辨识

0 引 言

空间观测等航天任务要求载荷实现毫角秒级的指向精度和极高的姿态稳定度[1]。而精密跟瞄Stewart平台具有高性能隔振、高精度指向和高稳定控制等优点，使得Stewart超静平台成为实现这类航天任务必不可少的一环[2-3]。Stewart超静平台准确的动力学参数是实现载荷高精度指向控制的可靠保障。同时，Stewart平台属于多通道耦合系统，准确的运动学参数有利于通道解耦以及控制器设计。然而，结构形变、安装偏差等因素造就了系统动力学参数实际值与理论值相差较大，这直接影响了Stewart超静平台控制性能。因此，辨识Stewart超静平台耦合模型动力学参数是实现其高精度指向控制必要前提。

获取超静平台载荷位姿信息是辨识动力学参数首要解决的问题。文献[4-5]提出采用计算机视觉图像处理算法获取Stewart超静平台的位移和姿态信息。这种信息获取方法仅适用于Stewart平台位移和姿态估计精度要求较低的场合。而应用于天文观测等航天任务的精密跟瞄Stewart平台，其要求运动范围小精度高，此时采用视觉测量获取载荷位姿具有以下局限性：1)很难获得摄像机坐标系与平台基坐标系之间的广义转移矩阵，2)无法精确实现摄像机坐标系位姿向基坐标系位姿转化[4]。文献[6]提出一种基于加速度测量的两刚体间相对姿态信息估计方法。该方法在仅有加速度可观测时，采用非线性Kalman滤波实现刚体间相对角速度和角加速度的估计。由于缺乏姿态测量信息，该方法无法对估计的角速度偏差进行修正，造成角速度及积分获得的姿态估计误差较大。文献[7]在研究火星进入过程中平动测量受限时，采用扩展Kalman滤波(EKF)估计加速度计零偏以及载荷的平动位移、速度信息。该算法需要精确获得航天器姿态和角速度信息以及迭代估计过程中的各个零偏之间协方差信息。

设计解耦方法是Stewart超静平台参数辨识另一个需要解决的问题。Stewart超静平台属于多输入多输出(MIMO)系统，平台各通道之间耦合特性复杂，不利于超静平台控制器设计。通过模型解耦实现多输入多输出系统转变为单输入单输出(SISO)系统，将极大的简化控制器的设计。文献[8-10]针对Stewart平台高耦合动力学模型，提出了一种基于关节空间质量-惯量解耦法，实现了Stewart平台MIMO模型到SISO模型的转换。同时采用最小方差约束和对称正定法辨识解耦模型动力学参数，从而提高Stewart平台载荷控制性能。文献[11-12]采用矩阵分解方法将Stewart超静平台由高度耦合的复杂多输入多输出系统变为多个相对简单的单输入单输出系统，从而简化了控制器的设计。

本文针对辨识Stewart超静平台耦合动力学参数需要解决的两个问题，设计了1)基于UKF的载荷位姿估计方法，实现了Stewart超静平台载荷广义位移、广义速度、广义加速度信息准确估计；2)基于Schur分解的动力学模型解耦方法，实现辨识模型中超静平台动力学参数显式表达。并将该方法应用到Stewart超静平台的动力学参数辨识中，仿真结果表明该方法正确可行。

1 问题的提出

1.1 辨识模型描述

针对Stewart超静平台动力学建模问题，国内外学者采用牛顿-欧拉法[13]、Kane[14]等方法给出了考虑不同因素的动力学模型。这些动力学模型都可采用多输入多输出的二阶系统进行描述。而工程实际中主要关心影响Stewart平台频率特性的刚度、阻尼等动力学参数。因此本文只考虑Stewart平台刚度和阻尼等因素进行动力学建模，系统描述为：

(1)

式中：M=diag(mp,mp,mp,Ix,Iy,Iz,)，mp为载荷的质量；Ix，Iy，Iz为载荷三轴主惯量；Ms为Stewart平台支杆质量参数阵，为对称正定矩阵。Jp为Stewart支杆对载荷质心作用力的雅克比矩阵；f为Stewart平台六个支杆驱动力；xp=[r,θ]为载荷的广义位移，r为载荷平动位移，θ为载荷姿态。fu为Stewart平台载荷受到来自星体平台干扰力；Cpp和Kpp分别为系统合成阻尼和刚度阵，定义为：

(2)

式中，C0=diag(c1,…,c6)，K0=diag(k1,…,k6)，ci、ki(i=1,2,…,6)分别为Stewart平台第i个支杆的阻尼和刚度系数。

(3)

式中，Jb为Stewart支杆对星体平台质心作用力的雅克比矩阵；xb为星体平台广义位移；Fd为载荷受到广义外作用力；Fc包含所有的科氏项；G包含所有的重力项。

对式(1)中的Stewart平台动力学参数辨识，需要解决两个问题。第一：载荷位姿信息确定方法。准确辨识式(1)的动力学参数，需要获取载荷广义位移、广义速度、广义加速度信息。加速度计能够测量系统的加速度，同时能够反映载荷的角速度信息。而且与陀螺相比，加速度计体积小、测量精度高，更适合Stewart平台这种小范围运动系统的测量。因此，有必要研究基于加速度测量的载荷位姿估计方法。第二：Stewart平台耦合模型解耦方法。由式(1)可知，Stewart平台载荷的位姿信息由六个支杆刚度和阻尼共同作用产生。因此，辨识动力学参数需要设计解耦方法，将耦合MIMO模型转变为SISO模型进行辨识。

1.2 测量系统描述

Stewart超静平台测量系统包括三个三轴加速度计A1、A2、A3和姿态敏感器。加速度计用于测量Stewart超静平台载荷平动信息。姿态敏感器测量Stewart超静平台载荷姿态。如图1所示，三个加速度计呈立体几何安装，三个加速度计测点在Stewart下平面坐标系Ob-XYZ(原点为下平面中心点Ob)的矢量距为ri(i=1,2,3)。

考虑Stewart平台载荷面安装i个三轴加速度计，则第i个三轴加速度计测量模型为：

(4)

式中，hi为第i个加速度计的三轴测量输出，Tib为Stewart平台载荷坐标系到第i个加速度计本体坐标系的方向余弦阵，α=[αx,αy,αz]T为载荷的x,y,z方向的平动加速度，ω=[ωx,ωy,ωz]T为载荷三轴角速度；=[x，y，z]T为载荷三轴角加速度；ηi=[ηix，ηiy，ηiz]T为第i个加速度计的测量噪声，为均值为0，方差σu的高斯白噪声；ω×为ω的反对称阵，定义为：

(5)

2 系统测量模型

2.1 观测系统建模

(6)

式中，I3×3为3×3的单位阵。

取三个加速度计测点矢量距分别为r1=[1,0,1],r2=[0,1,1],r3=[1,1,0]时，且方向余弦阵Ti=I3，则由式(4)知，由加速度计组成的测量系统的观测方程为：

(7)

考虑加速度计安装偏差，以及采用加速度计估计载荷角速度存在偏差等因素，需要在采用UKF估计载荷位姿信息基础上，采用序贯估计方法，引入姿态修正UKF估计载荷角速度偏差，提高载荷角速度收敛速度和估计精度。载荷角速度等效偏差参数估计及载荷角速度修正方法如下：

载荷运动学模型为：

(8)

(9)

δx=A2δx+B2u2

(10)

当采样时间为ΔT时，对测量系统式(6)、式(7) 的连续模型进行离散化，从而方便滤波器设计。式(6)的测量系统离散化状态方程为：

x(k+1)=Φ1x(k)+Γ1u1

(11)

式(7)测量系统离散观测方程为：

h(x(k-1))=[h1(x(k-1)) …h9(x(k-1))]T

(12)

式(10)误差状态方程离散形式为：

δx=Φ2δx+Γ2u2

(13)

测量系统离散模型的状态转移阵和输入阵定义为：

2.2 系统可观性分析

由系统可观性定义可知，如果系统可观测，则系统的状态能够通过有限观测量和输入量唯一确定。对于线性系统来说，系统可观为全局可观，系统中每个状态量都可以唯一确定。而离散系统式(11)中状态方程为线性模型，观测方程为非线性模型。对于非线性模型，需要构建可观性空间。通过可观性空间的秩准则进行可观性分析。采用李导数的方法构建系统的可观性空间为[6][15]：

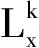
(14)

通过可观性空间O对状态x求导，构建可观性矩阵为：

(15)

通过判断可观性矩阵OM的秩分析系统的可观性。记：

(16)

式(16)中的子矩阵为：

对式(16)中OM1的每列分析可知，对于任意状态量x(x≠0)，矩阵OM1每一列是线性无关矢量，即rank(OM1)=9；

记

(17)

(18)

由式(16)、式(17)和式(18)可知，对于任意状态量x(x≠0)，构成观测矩阵OM的每一列为线性无关矢量，即rank(OM)=9。表明采用三个加速度计和姿态敏感器组成的测量系统能够实现Stewart超静平台载荷的平动和转动信息全观测。

2.3 基于UKF载荷位姿估计方法

无迹Kalman滤波摒弃了对非线性函数线性化的做法，采用无迹变换(UT)处理系统均值和协方差的非线性传递问题，没有忽略高阶项的误差，因此，UKF与EKF相比，估计精度更高。针对式(11)和式(13)的载荷位姿确定系统，文中采用UKF估计Stewart超静平台载荷平动和转动信息。如图2所示，采用序贯估计方法实现载荷的广义位移、广义速度和广义加速度准确估计。其中，第1-3步为标准的UKF估计过程。图2右侧中第4步采用姿态信息修正UKF估计载荷角速度偏差参数，进一步提高载荷姿态和角速度估计精度。

(19)

式中，qm为姿态敏感器测量的载荷姿态。Δqv为误差四元素Δq的矢量部分。误差系统的观测阵H2=[I3×303×3]。

3 动力学参数辨识

Stewart超静平台控制器带宽设计与自身刚度、阻尼等系数息息相关。Stewart超静平台支杆刚度、阻尼系数等受到热变形、外接线缆等的附加刚度等因素影响，使得Stewart超静平台支杆刚度、阻尼系数理论值与实际值差别较大。因此，辨识Stewart超静平台刚度、阻尼系数等动力学参数，有利于提高Stewart超静平台控制器性能。

为准确辨识动力学参数，需要获取载荷广义位移、速度、加速度信息。通过上节的UKF实现Stewart载荷平动加速度α，载荷姿态θ、角速度ω、角加速度的估计。通过对平台加速度α的积分，可得到平动速度v以及平动位移r。则，式(1)中的模型中广义加速度、广义速度、广义位移都可由UKF估计得到。Stewart超静平台动力学模型(1)中的刚度、阻尼等动力学参数与载荷位姿存在相互耦合，需要对动力学模型(1)进行解耦。令则动力学模型(1)改写为：

(20)

(21)

由上式可知，Mp为对称矩阵。采用Schur分解方法对Mp分解，则有：

Mp=V·u·VT

(22)

其中，V为单位正交阵，且满足VVT=VTV=I3。U为对角阵。由式(2)可知，刚度和阻尼矩阵K0，C0为对角阵。则式(20)中的矩阵Mp，K0，C0经过Schur分解可以转换为相互独立的对角阵。其中，VTMpV=u，VTK0V=K0，VTC0V=C0。

定义解耦模型中新的输入输出如下：

(23)

将上式(23)代入式(20)，则原系统的耦合动力学模型可转换为：

(24)

显然，上式中u=diag(u1，…，u6)，K0，C0都为对角阵。即采用Schur分解进行模型解耦，原动力学模型式(1)转换为SISO时不变系统。从而实现辨识模型中动力学参数显示表达。

定义辨识模型中状态量为Θ=[u1,…,u6,c1,…,c6，k1,…,k6]，将上述SISO模型式(24)改写为：

(25)

通过Schur方法解耦，式(25)实现了辨识Stewart平台刚度、阻尼等动力学参数的显式表达，采用递推最小二乘法，进行动力学参数辨识。

4 仿真校验

为了验证基于UKF的Stewart平台的姿态、角速度、角加速度估计的正确性，进行采用加速度计结合姿态敏感器测量信息的载荷位姿估计数学仿真。仿真参数见表1。在0-10 s进行Stewart超静平台载荷稳态控制。在10 s以后进行Stewart超静平台载荷沿x轴的姿态小角度机动和x方向的平动位移机动。在载荷同时具有平动和转动机动模式下，以载荷平动加速度、姿态角速度等估计误差为指标，校验UKF估计的正确性。

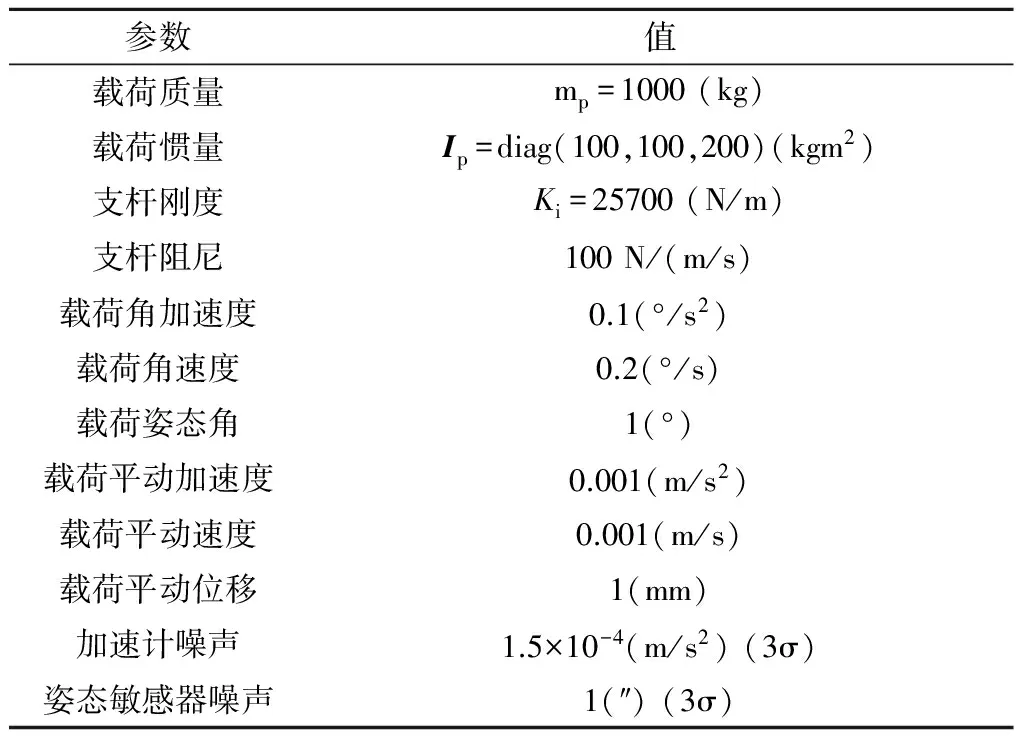
表1 仿真参数Table 1 Simulation parameters

采用上述UKF估计器能够实现Stewart超静平台载荷平动信息(包括加速度、速度、位移)和姿态信息(包括姿态角加速度、角速度、角位移)准确估计。采用最小二乘法进行Stewart平台动力学参数辨识。其中，Stewart平台支杆刚度系数直接关系着平台的结构频率，因此，辨识参数中主要以刚度系数为主。图7给出了Stewart平台6个支杆刚度辨识误差百分比仿真结果。由图可知，六个支杆的刚度辨识误差小于0.01。

5 结 论

针对辨识Stewart超静平台耦合动力学参数需要获取载荷广义位移、速度、加速度信息的问题，文中提出了一种基于加速度计结合姿态敏感器估计载荷位姿的方法。在建立测量系统状态模型和观测模型的基础上，采用UKF估计载荷平动加速度、角加速度、角速度、姿态信息。其载荷角速度估计误差优于0.005(°/s)。以UKF估计的载荷位姿信息为依据，采用最小二乘辨识超静平台耦合模型动力学参数，其六个支杆的刚度系数辨识误差小于0.01。

[1] Bronowicki A J. Vibration isolator for large space telescopes [J]. Journal of Spacecraft and Rockets, 2006, 43(01): 45-43.

[2] 徐高楠, 黄海, 李伟鹏, 等. 空间挠性结构的Stewart超静平台主动基座振动控制[J]. 宇航学报, 2015, 36(4): 439-445. [Xu Gao-nan, Huang Hai, Li Wei-peng, et al. Active vibration control of space flexible structure using Stewart platform as active base [J]. Journal of Astronautics, 2015, 36(4): 439-455.]

[3] 王萍萍, 刘磊. 柔性航天器高精度隔振与定向研究[J]. 宇航学报, 2012, 23(09): 1195-1202. [Wang Ping-ping, Liu Lei. Research on high accuracy pointing of flexible spacecraft with Stewart platform [J]. Journal of Astronautics, 2012, 23(09): 1195-1202.]

[4] 马瑾, 张国峰, 戴树岭, 等. 相对视觉位姿的Stewart超静平台运动学参数标定[J]. 系统仿真学报, 2016, 28(9): 2267-2274. [Ma Jin, Zhang Guo-feng, Dai Shuling, et al. Kinematic calibration of Stewart platform based on relative visual pose [J]. Journal of System Simulation, 2016, 28(9): 2267-2274.]

[5] Chevailer A, Copot C, Ionescu C M. Automatic calibration with robust control of a six DOF mechatronic system [J]. Mechatronics, 2016, 35:102-108.

[6] Schopp P, Graf H, Maurer M, et al. Observing relative motion with three accelerometer triads [J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(12): 3137-3151.

[7] Yu Z S,Crassidis J C. Accelerometer bias calibration using attitude and angular velocity information [J]. Journal of Guidance, Control, and Dynamic, 2016, 39(04): 741-753.

[8] Chen Y,McInroy, J E. Decoupled control of flexure-jointed hexapods using estimated joint-space mass-inertia matrix [J]. IEEE Transaction on Control Systems Technology, 2004, 12(3): 413-421.

[9] McInroy, J E. Modeling and design of flexure jointed Stewart platform for control purposes [J]. IEEE/ASME Transaction on mechatronics, 2002, 7(1): 95-99.

[10] Mcinroy J E, Hamann J C. Design and control of flexure jointed hexapods [J]. IEEE Transactions on robotics and automation, 2000, 16(4): 372-381.

[11] 王有懿, 汤亮, 何英姿. 一种超静平动主动指向容错控制方法[J]. 宇航学报, 2016, 37(12): 1457-1465. [Wang You-yi, Tang Liang, He Yin-zhi . Fault-tolerant control method for active pointing of ultra-quiet platform [J]. Journal of Astronautics, 2016, 37(12), 1457-1465.]

[12] 王晓雷, 杨庆俊, 郑钢铁. 八作动器隔振平台的通道耦合分析及解耦控制[J]. 宇航学报, 2007, 28(04): 245-249. [Wang Xiao-lei, Yang Qin-jun, Zheng Gang-tie. Decoupling analysis and decoupling control of vibration isolation platform with eight actuators [J]. Journal of Astronautics, 2007, 28(04), 245-249.]

[13] 刘磊, 王萍萍, 孔宪仁, 等. Stewart 平台动力学建模及鲁棒主动隔振控制[J]. 宇航学报, 2011, 32(06): 1231-1238. [Liu Lei, Wang Ping-ping, Kong Xian-ren. Dynamics modeling and robust active isolation control of Stewart platform [J]. Journal of Astronautics, 2011, 32(06): 1231-1238.]

[14] Yang J F,Xu Z B, Wu Q W, et al. Dynamics modeling and control of a 6-dof micro-vibration simulator. Mechanism and Machine Theory, 2016, 104: 350-369.

[15] Ning X L, Wang F, Fang J C. Implicit UKF and its observability analysis of satellite stellar refraction navigation [J]. Aerospace Science and Technology, 2016, 54: 49-58

ParameterIdentificationforUltraquietPlatformCouplingModelBasedonUKF

ZHANG Ke-bei1, WANG Da-yi2, WANG You-yi1

(1. Beijing Institute of Control Engineering, Beijing 100190, China; 2. Beijing Institute of Spacecraft Engineering, Beijing 100190, China)

A method based on Schur decomposition and unscented Kalman filter (UKF) is designed to identify the parameters of the Stewart coupling model. The state model, measurement model and observability are given. The UKF is adopted to determine the payload position and attitude. The attitude measurements are used in the UKF to correct the angular velocity error so that the estimation accuracy and convergence speed of the angular velocity can be improved. The payload generalized displacement, generalized velocity and generalized acceleration should be obtained. The parameter decoupling method is designed and the least squares method is used to identify the dynamics parameters. Numerical simulations results indicate that the angular velocity is estimated accurately by the UKF and the stiffness identification errors of the Stewart six struts are less than 0.01.

Stewart ultraquiet platform; Position and attitude determination; Unscented Kalman filter (UKF); Parameter identification

2017- 06- 15;

2017- 09- 25

国家杰出青年科学基金(61525301)；国家自然科学基金重大项目课题(61690215)

TB535

A

1000-1328(2017)12- 1289- 08

10.3873/j.issn.1000- 1328.2017.12.005

张科备(1985-)，男，博士生，主要从事航天器姿态高精高稳控制。

通信地址：北京市中关村南三街北京控制工程研究所(100190)

E-mail:zhangkb.2008@163.com