耦合混合变量的空间机动飞行器多学科设计优化

粟 华，王京士，龚春林，谷良贤，李 波，张孝南

(1. 陕西省空天飞行器设计重点实验室，西安 710072；2. 西北工业大学航天学院，西安 710072；3. 上海卫星工程研究所，上海 220240)

耦合混合变量的空间机动飞行器多学科设计优化

粟 华1, 2，王京士3，龚春林1, 2，谷良贤1, 2，李 波2，张孝南2

(1. 陕西省空天飞行器设计重点实验室，西安 710072；2. 西北工业大学航天学院，西安 710072；3. 上海卫星工程研究所，上海 220240)

针对复杂耦合下的空间机动飞行器(SMV)多学科设计优化(MDO)问题，开展了同时考虑连续-离散混合变量的MDO求解技术研究。考虑空间机动飞行器总体方案设计需求，建立了包括轨道分系统、电源分系统、结构分系统、推进分系统、GNC分系统等多个学科的空间机动飞行器MDO模型；提出了基于变量转化法的混合变量MDO求解策略，将连续-离散混合变量MDO问题转化为普通MDO问题进行优化求解。优化后的空间机动飞行器总质量相比于初始方案降低了18.1%，证明了本文方法的有效性。与将离散变量作为连续变量优化的直接方式对比分析表明，本文提出的基于变量转化法的混合变量MDO求解策略在求解效率和可靠性方面更优。

空间机动飞行器；多学科设计优化；混合变量优化；多学科求解策略；变量转化法

0 引 言

空间机动飞行器(Space maneuvering vehicle，SMV)是一种携带有效载荷，由火箭发射入轨后在空间进行机动、交会对接，对航天器进行在轨服务的航天器。SMV由有效载荷分系统、结构分系统、电源分系统，制导导航和控制(GNC)分系统、推进分系统、防热分系统、测控与通信分系统、数据管理分系统等多个相互关联的分系统组成，其总体设计优化是一个典型的复杂多学科耦合问题。

20世纪80年代出现的考虑复杂学科耦合关系并充分发掘设计空间潜力的多学科设计优化(Multidisciplinary design optimization，MDO)方法，目前已经被大量应用于SMV等复杂对象的设计优化中，以进一步发掘设计潜力并提升飞行器的综合性能。Mosher[1]对比了多种MDO技术在SMV概念设计中的应用，最终选择基于遗传算法的MDO方法，创建了SCOUT软件工具，应用于NEAR、MGS和Eagle-eye等月球探测器的MDO设计中；Cullimore等[2]基于包含光、热和结构的数字分析模型实现了基于ISIGHT软件的空间机动飞行器优化；姚雯等[3]将不确定性思想运用到卫星总体设计中，实现了不确定性影响下的卫星总体优化设计；王振国等[4]分析了卫星总体设计中轨道设计、卫星设计和发射选择间的耦合关系与协同效应，实现了月球探测卫星的MDO概念设计；郭忠全[5]研究了卫星的变复杂度建模方法，开发了“卫星总体方案多学科综合设计原型系统”软件；吴蓓蓓等[6]将解析目标分流策略应用到海洋卫星的MDO设计，实现了基于ATC方法的卫星总体参数优化；裴晓强等[7]、黄海等[8]研究了卫星总体参数优化过程，实现了基于遗传算法的协同优化方法在卫星总体设计中的应用。

MDO方法虽然在卫星等飞行器设计过程中得到了较多应用，但通常都假设设计变量是连续的。在实际工程设计中，设计变量有可能为离散的，例如太阳能电池板的数量只能取整数，姿控推力器的推力只采用现有的姿控推力器推力。因此，实际上的复杂工程问题的MDO是一个涉及连续-离散混合变量的优化问题，必须开展支持混合变量的MDO求解技术研究。目前，混合变量优化算法研究已经取得了一定的成果[9]，但在考虑复杂耦合下的MDO问题中应用很少。王威等[10]利用分而治之的混合参数处理机制，提出了一种多学科混合变量协同优化方法，并通过简单的数学算例证明其可行性和有效性，但其在复杂MDO问题的应用效果未知；范丽等[11]针对强约束条件下的混合变量星座构形问题，提出了以进化算法为基础的一体化优化设计方法；陈琪锋等[12-13]采用分布式协同进化MDO算法，对同时包含星座设计优化和卫星优化的海洋监视卫星星座系统进行了考虑混合变量的多学科优化设计。实际上由于进化算法求解效率不高，在面临复杂学科模型时可能会面临计算量过大的问题。因此，本文以包含多学科复杂耦合并存在连续-离散混合变量的SMV为研究对象，建立各学科模型和考虑混合变量的MDO问题，基于变量转化法[14]开展考虑混合变量的MDO求解策略研究，以提高其综合性能。

1 SMV总体方案

1.1 飞行任务

SMV是一种用于静止轨道在轨服务的新型航天器，其基本任务包括在轨维修、燃料加注、辅助离轨、轨道碎片清理等。SMV平时停留在停泊轨道上，需要进行服务任务时，机动到目标航天器处进行服务操作，完成服务任务后，航天器再回到停泊轨道上。其主要任务方案设定如图1所示。

1.2 任务方案

针对上述飞行任务要求，SMV的总体外形方案和结构布局方案设计如图2、图3所示。SMV包含轨道、结构、电源、GNC、推进、热控、通信、数据管理八个分系统。各分系统的初始方案选择如图1所示。

轨道学科采用霍曼转移进行轨道机动。针对上述飞行任务需求，典型的轨道包括在轨维修机动轨道、轨道清理机动轨道、燃料加注机动轨道和辅助离轨机动轨道等。

结构分系统采用桁条式加筋的中心承力筒结构。壳体主承力结构为中心承力筒，或简称承力筒，它是一个筒形结构。

电源分系统负责在SMV的整个寿命期间为用电负载提供电能，包括发电装置、电源控制装置和储能装置。发电装置采用三结砷化镓太阳能电池，储能装置采用锂离子蓄电池。

姿态控制分系统采用三轴稳定式，执行机构选择飞轮加推力器，姿控推力器用于对反作用飞轮进行动量卸载，同时作为执行机构用于姿态机动。

推进分系统的轨道控制与姿态控制使用独立的推力器以实现轨道机动。推进分系统选择N2O4与MMH的双组元推进系统。选取挤压式供应方式作为发动机推进剂供应方式。

热控分析系统采用在SMV表面安装散热面进行热防护。经分析可定性得出SMV的+Y和-Y长期指向轨道平面法向，太阳辐射热流较小。选择这两个面作为主散热面，其涂层材料选用S781有机白漆；其它表面采用玻璃二次表面镜(Optical solar reflector,OSR)。

通信分系统负责SMV与地球或SMV与其他卫星之间的接口，包括转发器、滤波器、射频开关、双工器、天线等。

数据处理分系统负责接收指令，并将其译码、处理、分配。其包括遥测及指令单元、远程单元、计算机、存储部件等。

为降低优化难度，对上述方案进行适当简化：参照相似规模和任务的SMV，直接给定防热、通信和数据管理分系统的设计方案，只对轨道、结构、电源、推进、GNC等5个分系统进行优化设计。

2 学科建模

2.1 轨道学科

根据SMV的飞行任务方案，可知航天器大部分时间都处于停泊轨道上，典型的机动轨道如图4和图5所示。因此，主要考虑航天器的姿态稳定，每隔一段时间对其进行一次动量卸载。根据飞行器任务方案，确定不同任务采用的轨道机动策略，分析计算轨道机动参数。

在进行轨道机动速度增量计算的时候主要涉及到圆轨道速度v、椭圆轨道近地点速度vp和椭圆轨道远地点速度va。计算模型如下：

(1)

式中：μ为地球引力常数，r为圆轨道半径，rp为近地点高度。轨道学科采用C#编程调用卫星工具包(Satellite tool kit,STK)完成任务仿真过程。

2.2 电源学科

根据SMV各工作模式，电源系统的工作流程如图6所示。通过太阳能电池面积和实时入射角求解太阳能电池实时提供功率：

Pb(t)=AsaFsηaIdcosλ(t)(1-dy)t/Tlife

(2)

式中：Asa为太阳能电池板面积，Fs为太阳辐射强度，ηa为太阳能电池转换效率，Id为固有退化系数，λ为轨道学科输出入射角，dy为太阳电池阵输出功率年下降率，Tlife为飞行器寿命。

电源学科采用C++编程实现。经计算得到太阳能电池板高度hsa，蓄电池高度lzr和电池质量Mr。

2.3 GNC学科

GNC的任务主要包括轨道确定、轨道控制、姿态稳定及姿态机动控制，其计算流程如图7所示。

在每次进行轨道机动前后都要进行姿态调整，设定调整方案为在ta的时间里能够姿态调整θ。其中，5%时间用于加速，90%时间用于惯性滑行，5%时间用于减速。主要性能参数计算如下：

惯性滑行速度：

(3)

所需加速度：

(4)

所需姿控推力器推力：

(5)

式中：Imax为最大转动惯量，L为姿控推力器力臂。根据Fz选择合适的姿控推力器质量mz和功率Pz。干扰力矩的求解采用文献[8]中的求解方法，这里不再赘述。学科设计变量包括飞轮角动量容量Hwheel和推力Fz。

2.4 推进学科

推进学科分析过程包括推力室设计分析、储箱设计分析以及高压气瓶设计分析。推进学科设计计算分析流程如图8所示。

燃烧室设计的主要数学模型如下：

理想空间比冲：

(6)

实际空间比冲：

(7)

发动机推力：

(8)

推进系统的质量和功率如下：

Mpropel=mengine+mo+mf+mafuel+mgas+mtrans

(9)

(10)

2.5 结构学科

SMV的结构设计主要用于承载整星主要载荷、安装卫星上的部分设备、提供卫星与运载火箭连接与分离的接口等。其主要建模流程如下：首先，建立CATIA参数化几何模型；然后在HyperMesh中进行划分网格、赋予材料单元属性、设置载荷条件和静力学求解设置，生成BDF格式的结构分析模型；最后，Patran读入上述BDF文件后完成优化任务配置并最终提交Nastran分析；计算结果由Patran后处理并保存输出。建立的SMV结构参数化几何模型与有限元分析模型如图9所示。学科设计变量包括结构中心承力筒半径R。

2.6 防热学科

防热学科采用给定热控方案。各主要部分的热控方案如表1所示。

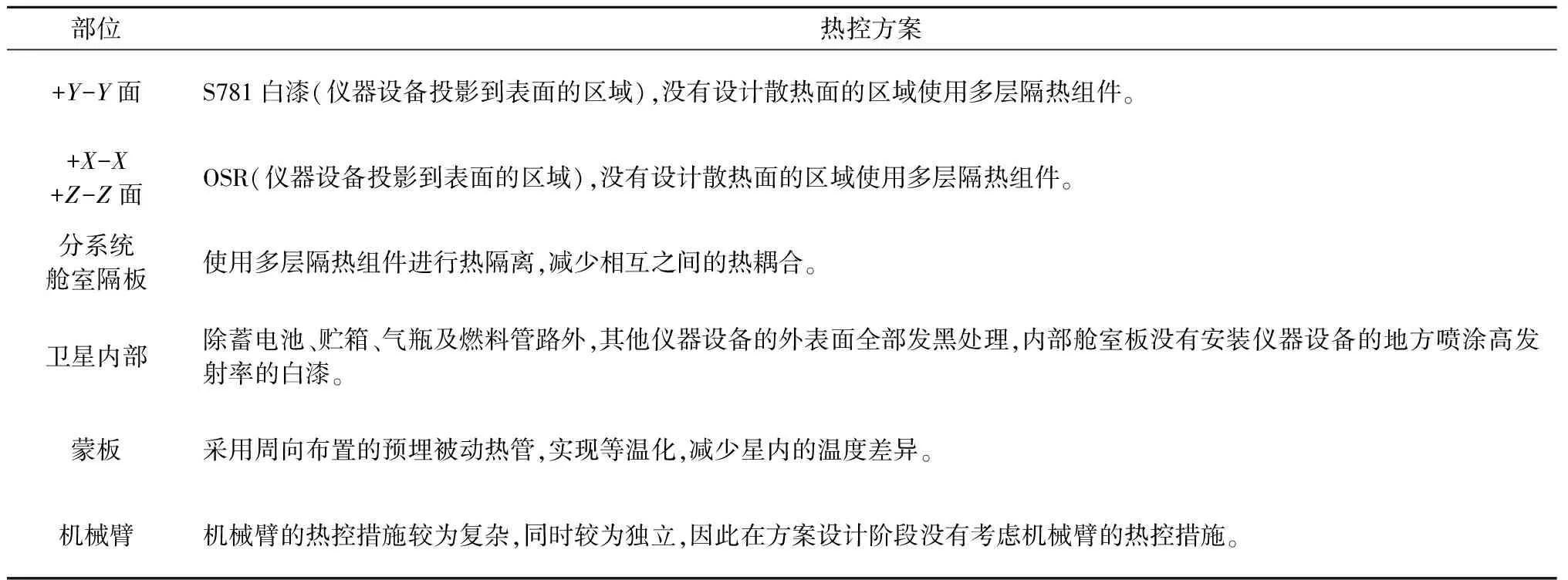
表1 SMV的热控方案Table 1 Thermal control scheme of the SMV

2.7 通讯学科

通讯学科采用给定方案。借鉴典型S波段TDRSS用户通信分系统，设置通信系统组成及主要指标如表2所示。通信系统的总质量为55.74 kg，总功率为62.5 W。

表2 SMV的通信方案Table 2 Communication scheme of the SMV

2.8 指令与数据处理学科

指令与数据处理学科采用给定方案。其组成及主要指标如表3所示。指令与数据处理分系统总质量55 kg，总功率102.8 W。

表3 SMV的指令与数据处理方案Table 3 Command and data handling scheme of the SMV

3 空间机动飞行器混合变量MDO

3.1 SMV-MDO问题

根据各学科间耦合关系，SMV-MDO问题的设计结构矩阵如图10所示，包含轨道、电源、推进、GNC和结构5个学科。其中，Xmission和Xdiscipline分别表示系统级共享设计变量和学科设计变量。

对应的多学科优化问题如下：

minMsum

findXOrbit,XBattery,XPropel,XGNC,XStr

s.t.

实际工程中为降低研发成本，推进器和姿控推力器通常直接选择现有型号。对应的设计变量实际上为离散变量，包括：GNC学科的姿控器推力Fz，推进学科的燃烧室收敛面积比εc和喷管扩张面积比ε。此时对应的MDO问题变为一个同时包含连续变量和离散变量的混合变量MDO问题，无法直接采用传统的MDO方法进行优化求解。因此，本文提出一种基于变量转化法的混合变量MDO求解架构。

3.2 基于变量转化的混合变量MDO求解架构

目前，求解连续-离散混合变量优化问题的方法主要包括分而治之策略、离散变量连续化、连续变量离散化等。实际应用时由于优化问题的复杂性，上述方法都存在计算量大、实现复杂等问题。考虑到MDO求解策略对优化问题的连续性、可微性要求，本文在多学科可行(Multi-disciplinary feasible，MDF)方法的基础上，提出一种基于变量转化法的混合变量MDO求解架构，利用变量转化法将离散变量转化连续变量，以实现基于梯度优化算法的高效优化求解。

1)变量转化法

变量转化法对于每一个优化变量设定一个名义变量，名义变量的取值范围统一在[0, 1]区间以保证设计空间均衡。根据优化变量的类型和取值范围，通过以下规则将名义变量转化为实际离散变量。定义k为名义变量，则有连续变量xc：

xc=a+bk

(12)

离散变量xd：

xd=a+c·floor(bk)

(13)

式中：a,b,c为转换系数，floor表示将变量k向负无穷大方向取整。例如对于连续变量x1和离散变量x2有x1∈[1, 4]，x2∈{1, 2, 3, 4, 5}。定义名义变量k1，k2满足k1∈[0, 1],k2∈[0, 1]，则x1和x2可由k1，k2通过以下转化关系得到：

x1=1+3k1

x2=1+1.0·floor(4k2)

经过变量转化后的名义变量在其连续取值区间内的所有取值转化为实际优化变量的所有取值，将转化后的实际优化变量代入原问题，既可将其转换为连续变量优化问题进行优化求解。优化后得到的名义变量的最优解通过式(12)和式(13)转化即可得到实际变量最优解。

2)基于MDF的混合变量MDO求解策略

MDO求解策略是MDO问题的数学表述及其在计算环境中实现的过程组织[15]。常用的求解策略包括MDF、单学科可行方法(Individual discipline feasible，IDF)、并行子空间优化(Concurrent subspace optimization，CSSO)、协同优化(Collaborative optimization，CO)等。由图10可知，SMV-MDO问题的学科间耦合十分紧密，轨道学科与其他学科的耦合变量均为高维向量，如果采用IDF、CO等直接解耦耦合变量的求解策略，由于耦合变量被作为系统级优化变量参与系统级优化过程，会大幅度增加系统级的优化问题规模，从而加大MDO问题的求解难度。因此，本文采用基于多学科分析(Multidisciplinary analysis，MDA)过程的MDF求解策略来实现其优化求解。

MDF方法包含两个迭代过程：一个是优化迭代过程，另一个是MDA迭代过程。在优化迭代过程中嵌套着MDA迭代过程，MDA过程经过多次迭代使得学科间耦合变量满足相容性条件。两次迭代变量的相对误差小于给定收敛标准即为满足相容性约束。这里采用SMV的总质量Msum变化和姿控推力器比冲Izt变化作为MDA收敛依据：

(14)

由于离散变量的存在，实际优化迭代过程中会出现：当离散优化变量改变较小时，转换后的实际优化变量不变，导致MDA过程重复计算，额外消耗大量计算时间。为避免上述过程，建立迭代历程数据库，保存每一步的实际优化变量和MDA收敛后的耦合变量。在进行下一步迭代前，对当前步的实际优化变量与迭代历程数据库中的历史数据进行对比，相同时则直接读取迭代历程数据库中的耦合变量，以避免额外的MDA计算消耗。

3.3 SMV-MDO求解流程

基于MDF求解策略的SMV-MDO问题的求解流程如图11所示。其中，迭代历程数据库用于保存每一步的实际优化变量和MDA收敛后的耦合变量。详细的实现流程如下：

1)通过变量转化法将系统级混合变量X0转化为连续变量K0。

2)优化器给出当前步MDA的初始值K。

3)将K转换为实际变量X并与迭代历程数据库进行匹配分析，存在相同X则退出MDA过程，将数据库中的对应耦合变量Y返回给优化器计算目标函数和约束条件，进入下一步系统级优化。迭代历程数据库不存在则进入4)。

4)通过牛顿迭代法进行MDA过程迭代直到学科间的耦合变量满足相容性收敛标准。

5)将满足学科相容性约束的实际变量X′和对应的耦合变量Y′存入迭代历程数据库。

6)将满足学科相容性约束的当前解及各学科输出的状态变量传给顶层优化器，进行系统优化。

7)优化器计算出下一步改进的优化变量值、判断优化收敛;如不收敛,则进入下一轮优化过程;如收敛,则退出。

不断重复以上过程最终既可得到满足学科相容约束的最优设计点。

4 优化结果与结果分析

4.1 优化设置

在MATLAB环境中集成上述学科分析模型。其中，轨道学科通过C#编写脚本调用STK完成学科分析；电源、推进、GNC等学科由C++编写接口并完成集成；结构学科内部集成CATIA、HyperMesh、Patran、Nastran完成结构分析。初始方案如下：

电源学科：Asa 0=9.1m2，mr 0=127 kg

推进学科：α0=45°，At 0=0.0049 m2，ε0=25，εc 0=1.8

GNC学科：Hwheel0=13.35 Nms，Fz 0=7 N

轨道学科：Horbit 0=35586 km

结构学科：R0=700 mm

推进学科与GNC学科均包含离散变量，采用变量转化法将其转换为名义变量：

推进学科：kα 0=1.0，kAt 0=0.1，kε 0=0.82，kεc 0=0.8

GNC学科：kHwheel 0=0.7，kFz 0=0.7

在优化求解时，为降低计算规模，仅考虑电源、推进和GNC三个学科的设计分析，轨道和结构学科不作为设计部分仅作为分析过程。

4.2 优化结果

采用第3节中的方法对上述SMV-MDO问题进行优化求解。系统级求解器使用序列二次规划算法。鉴于混合变量优化问题在离散变量处存在梯度搜索困难，本文通过增大梯度搜索的步长来改善搜索性能。

目标函数的迭代过程如图12所示。SMV的总质量随着迭代收敛逐渐减少，从初始的4581.7 kg降至3753.8 kg，减少了18.1%。

主要约束条件的迭代历程见图13～图15。在整个优化过程中，各约束量均满足设计要求；从约束量的变化可知，初始方案的设计裕度较大，通过逐步压缩约束量裕度，使约束量逐步靠近约束边界，从而降低了SMV总质量。

优化前后各学科的设计变量对比如表4所示。从表4可以看出，各学科的设计变量相比于优化前都有较大变化。离散变量姿控器推力Fz和燃烧室收敛面积比εc分别由初始的7 N和1.8改变为优化后的5 N和1.2，这说明本文提出的基于变量转化的混合变量MDO求解架构成功实现了包含混合变量的SMV多学科优化设计。

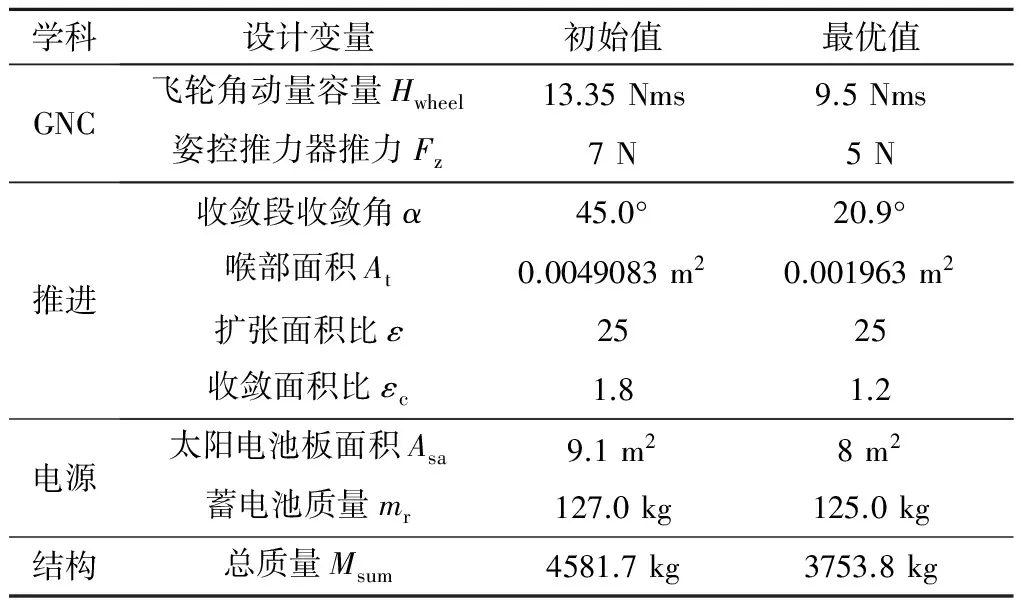
表4 优化前后主要设计变量对比Table 4 Comparison of the design variables before and after optimization

4.3 与直接优化结果对比

从上述优化结果可以看出，采用变量转换方法处理后的离散变量MDO问题能够快速收敛到最优解。本节将变量转换方法与直接优化进行对比。直接优化法指将离散变量直接作为连续变量带入优化算法进行优化，学科模型则作四舍五入处理。

直接法仍采用MDF策略和序列二次规划算法。直接法优化得到的目标函数迭代历程如图16所示。两种方法的优化结果对比如表5所示。从表5可以看出，两种方法优化后的最优方案中Hwheel和α差异较大，其余设计变量均相同。直接优化方法未处理的优化结果目标函数值为3736.7 kg，要优于变量转化法的目标函数值3753.8 kg，但其设计变量并不在设计空间内。将其圆整后计算得到的最优目标函数值为3766.3 kg。可以看出，直接优化方法在收敛过程中，由于设计变量并不一定在原设计空间内，导致最终结果是不可行的，对其圆整处理可能会造成性能下降。因此，变量转换法相比于直接优化方法避免了圆整后造成的性能下降和额外分析，更适合求解混合变量MDO问题。

从求解效率来看，直接优化法和变量转换法的MDA过程的迭代次数分别为101次和111次。变量转换法采用了改进的基于MDF的混合变量MDO求解策略，由于迭代历程数据库的存在，防止迭代后期大量的学科分析重复计算，直接优化法和变量转换法对应的学科分析模型的总计算次数分别为987次和913次。变量转换法的实际求解效率相比于直接优化法要更好。

从图12～16可以看出，两种方法在收敛中后期都存在收敛曲线趋于平缓，在局部小范围波动，算法收敛缓慢的问题。这说明由于各种基于数值分析的高拟真度学科模型的引入，增加了设计空间的非光滑性，导致梯度优化算法后期收敛困难。改进的基于MDF的混合变量MDO求解策略由于采用了迭代历程数据库，可以防止算法后期学科分析的重复计算，可以进一步提高计算效率。

表5 变量转化方法和直接优化方法的优化结果对比Table 5 Optimization result comparison between variable transformation method and direct optimization method

5 结 论

随着对飞行器设计要求的不断提高，现代飞行器设计问题的复杂程度日益增加。一方面，基于数值分析的高拟真度学科模型的使用越来越普遍，增加了计算时间并导致设计空间非光滑；另一方面，对应的MDO问题也由于耦合关系的增多和混合变量问题的出现变得越来越复杂，求解难度更大。迫切需要发展求解能力更强，效率更高并支持混合变量的MDO求解策略及其集成架构。

本文以复杂多学科耦合下的SMV为研究对象，建立了耦合混合变量的MDO模型及其学科分析模型，提出了基于变量转化法的改进MDF求解策略，通过避免直接优化方法圆整后造成的性能下降和额外分析，提高了整体求解效率和可靠性。本文研究为存在混合变量的现代飞行器MDO问题提出了一套可行且有效的解决途径，可为类似复杂MDO工程问题的优化设计提供参考。

[1] Mosher T.Improving spacecraft design using a multidisciplinary design optimization methodology[D]. Colorado: University of Colorado, 2000.

[2] Cullimore B, Panezak T, Baumann J, et al.Automated multidisciplinary optimization of a space-based telescope[R]. SAE 2002-01-2445, 2002.

[3] 姚雯, 陈小前, 赵勇. 基于不确定性MDO的卫星总体优化设计研究[J]. 宇航学报, 2009, 30(5):1808-1815. [Yao Wen, Chen Xiao-qian, Zhao Yong. Research on satellite system design based on uncertainty multidisciplinary design optimization[J]. Journal of Astronautics, 2009, 30(5):1808-1815.]

[4] 王振国, 陈小前, 罗世彬. 飞行器多学科设计优化理论与应用研究[M]. 北京: 国防工业出版社, 2004. [Wang Zhen-guo, Chen Xiao-qian, Luo Shi-bin. Aircraft multidisciplinary design optimization theory and application[M]. Beijing: National Defense Industry Press, 2004.]

[5] 郭忠全. 多学科设计优化方法在卫星总体设计中的应用研究[D]. 长沙: 国防科技大学, 2005. [Guo Zhong-quan. Study and application of MDO method in the system design of satellite[D]. Changsha: National University of Defense Technology, 2005.]

[6] 吴蓓蓓, 黄海, 陈珅艳, 等. 使用解析目标分流策略的海洋卫星多学科优化[J]. 宇航学报, 2013, 34(1):9-16. [Wu bei-bei, Huang Hai, Chen Shen-yan, et al. Multi-disciplinary design optimization of ocean satellites based on analytical target cascading strategy[J]. Journal of Astronautics, 2013, 34(1):9-16.]

[7] 裴晓强, 黄海. 协同优化在卫星多学科设计优化中的初步应用[J]. 宇航学报, 2006, 27(5):1054-1058. [Pei Xiao-qiang, Huang Hai. Multidisciplinary design optimization of satellites using collaborative optimization[J]. Journal of Astronautics, 2006, 27(5):1054-1058.]

[8] Huang H, An H, Zhang L, et al. Multidisciplinary design modeling and optimization for satellite with maneuver capability[J]. Structural & Multidisciplinary Optimization, 2014, 50(5):883-898.

[9] 张伟. 人工蜂群混合优化算法及应用研究[D]. 杭州: 浙江大学, 2013. [Zhang Wei. Research on artificial bee colony based hybrid optimization algorithms and applications[D]. Hangzhou: Zhejiang University, 2013.]

[10] 王威, 范文慧, 肖田元,等. 多学科混合变量协同设计优化方法研究[J]. 控制与决策, 2011, 26(8):1243-1247. [Wang Wei, Fan Wen-hui, Xiao Tian-yuan, et al. Study of mix-variable collaborative design optimization[J]. Control and Decision, 2011, 26(8):1243-1247.]

[11] 范丽, 张育林. 强约束条件下星座一体化优化设计方法研究[J]. 宇航学报, 2006(4):779-782,797. [Fan li, Zhang yu-lin. An integrated design optimization method for satellite constellation with powerful constraints[J]. Journal of Astronautics, 2006(4):779-782,797.]

[12] 陈琪锋, 戴金海. 卫星星座系统多学科设计优化研究[J]. 宇航学报, 2003(5):502-509,533.[Chen qi-feng, Dai jin-hai. Multidisciplinary design optimization of satellite constellation system[J]. Journal of Astronautics, 2003(5):502-509,533.]

[13] 陈琪锋, 戴金海. 异步并行的分布式协同进化MDO算法研究[J]. 宇航学报, 2002(4):57-61. [Chen qi-feng, Dai jin-hai. Asynchronous parallel distributed coevolutionary multidiscip-linary design optimization[J]. Journal of Astronautics, 2002(4):57-61.]

[14] 连青惠, 蓝兆辉. 基于变量转化法的混合离散变量优化设计[J]. 机械传动, 2015(5):90-92. [Lian Qing-hui, Lan Zhao-hui. Optimization design of mixed discrete variable based on variable transformation method[J]. Journal of Mechanical Transmission, 2015(5):90-92.]

[15] 粟华. 再入飞行器多学科优化技术研究[D]. 西安: 西北工业大学, 2008. [Su Hua. Multidisciplinary design optimization of reentry flight vehicle[D]. Xi’an: Northwestern Polytechnical University, 2008.]

[16] Huang D H, Huzel D K. Modern engineering for design of liquid-propellant rocket engines[M]. Washington: American Institute of Aeronautics & Astronautics, 1992, 147.

MultidisciplinaryDesignOptimizationofSpaceManeuveringVehicleCouplingwithMixedVariable

SU Hua1, 2, WANG Jing-shi3, GONG Chun-lin1, 2, GU Liang-xian1, 2, LI Bo2, ZHANG Xiao-nan2

(1. Shanxi Aerospace Flight Vehicle Design Key Laboratory, Xi’an 710072, China;2. College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;3. Shanghai Institute of Satellite Engineering, Shanghai, 220240, China)

To solve the multidisciplinary design optimization (MDO) problem of a space maneuvering vehicle (SMV) under complex interdisciplinary coupling, a MDO solution technique considering continuous-discrete mixed variables is developed. Based on the requirements of the SMV conceptual scheme design, a MDO model containing orbital system, power system, structure system, propulsion system and GNC system is constructed. For the corresponding mixed variable MDO problem, a modified MDO architecture is proposed to solve the corresponding mixed variable MDO problem via variable transformation method and a mixed variable MDO process. Total mass of the optimized SMV has been reduced by 18.1% compared with the original scheme, the effectiveness and applicability of this proposed method are proved. The comparison between the variable transformation method and the direct optimization method indicates that the method proposed in this paper has a better efficiency and reliability over the others.

Space maneuvering vehicle (SMV); Multidisciplinary design optimization (MDO); Mixed variable optimization; MDO architecture; Variable transformation method

2017- 06- 02;

2017- 10- 09

国家自然科学基金(51505385)；国防基础科研计划(JCKY2016204B102，JCKY2016208C001)；中央高校基本科研业务费专项基金(3102015BJ(Ⅱ)JGZ002)

V421.1

A

1000-1328(2017)12- 1253- 10

10.3873/j.issn.1000- 1328.2017.12.001

粟华(1985-),男，博士，助理研究员,主要从事飞行器总体设计、多学科设计优化方法及其工程应用方面的研究。

通信地址：陕西省西安市友谊西路127号西北工业大学航天学院(710072)电话: 15091676096

E-mail: su@nwpu.edu.cn