长期姿控扰动情况下空间实验室轨道影响分析及建模

张 宇，周 立，孔 静，韩 意，段成林

(北京航天飞行控制中心，北京 100094)

长期姿控扰动情况下空间实验室轨道影响分析及建模

张 宇，周 立，孔 静，韩 意，段成林

(北京航天飞行控制中心，北京 100094)

针对空间实验室连续偏航飞行模式的特点，分析长期姿控喷气对轨道的影响，设计大尺度航天器的天线相位中心修正算法，同时建立空间实验室组合体连续偏航飞行时姿控喷气的经验力补偿模型，解决了连续偏航飞行阶段的动力学精密定轨和预报问题。然后利用动力学建模分析了连续偏航期间的姿控喷气影响，其中每圈累积的速度增量在轨道系各方向上均小于1 cm/s，由轨道解算和遥测计算可知速度增量的量级一致。最后利用建模算法分析比较了空间实验室连续偏航飞行阶段的轨道精度，增加经验力模型补偿后的定轨精度优于10 m，预报1天的精度相比无经验力模型提高了1倍。

空间实验室；连续偏航；姿控喷气；精密定轨；轨道动力学；模型补偿；相位修正

0 引 言

2016年9月15日，天宫二号空间实验室及其搭载的空间应用系统伴随卫星在酒泉卫星发射中心由长征二号火箭发射升空。2016年10月17日，神舟十一号搭载2名航天员在酒泉卫星发射中心发射，神舟十一号飞船在393 km轨道与天宫二号飞行器进行交会对接，形成空间实验室组合体，提供天宫二号在轨运营所需人员、物资和试验载荷的往返运输服务，开展在轨试验，验证空间站阶段载人飞船相关技术，释放伴随卫星完成相关在轨试验[1]。

为满足空间实验室组合体的能源需求，太阳能帆板法向需指向太阳，当太阳位置与轨道面夹角较小时，可以通过控制帆板转向，使其指向太阳，此时充电效率可以满足器上载荷的需求；但是当太阳位置与轨道面夹角较大的时候，调整帆板转角已不能保证太阳入射角条件，充电效率小于器上载荷的功率，此时需要将空间实验室的飞行模式由三轴对地转为连续偏航，所以在我国载人航天飞行中首次实施了组合体(天宫二号与神舟十一号)连续偏航模式飞行。在天宫一号飞行试验以及神舟飞船拓展试验时实施了连续偏航飞行[2-3]，但是均为单体连续偏航，飞行时姿态控制模式均为动量轮控制。空间实验室组合体连续偏航与单体连续偏航的差异除质量、大气阻力迎风面积的差异外[4-5]，还包括组合体这类大尺度复杂航天器的测量接收机相位中心修正，组合体的连续偏航的姿控模式采用姿控发动机喷气控制，发动机喷气除控制姿态以外，还对飞行轨道产生扰动，影响空间实验室组合体定轨和预报的精度。

空间实验室的组合体质心位置由两目标各自的质心转变为组合飞行后的共同质心，空间实验室的信号接收天线与其实际质心位置差异会导致空间实验室的定轨产生十米量级的误差。计算时需要将天线的测量信号修正到质心，不同飞行模式下天线的相位中心修正算法不同，但是均可通过飞行姿态进行归算。连续偏航飞行模式下需要组合体的帆板法向指向太阳，当组合体转入该模式后的迎风面积与单体模式存在较大差异，轨道计算中通过求解大气阻力系数Cd，将迎风面积和质量的误差吸收到大气阻力系数中，进而改善定轨拟合精度[6-13]。姿控力是在航天器调姿或动量轮卸载时，由姿控发动机喷气引起的轨道摄动作用力，通常持续时间较短，但是空间实验室组合体为保持连续偏航飞行姿态，姿控力持续时间长达数天，姿控力的影响问题可通过建立相应的动力学模型来解决，但是其精度受姿控发动机精度、遥测参数精度和姿态控制精度等因素的影响，难以直接使用相关参数进行轨道动力学的补偿，通常需要结合轨道改进的过程求解姿控作用力的摄动加速度[14-15]。

本文对组合体姿控喷气的轨道影响进行分析，从动力学角度出发，建立适用于定轨和预报的模型，下面给出空间实验室连续偏航的示意图。

1 天线相位中心修正

1.1 组合体质心计算

组合体本体系定义如下：以组合体对接口为本体系原点，本体系三轴方向与天宫本体系三轴方向一致。空间实验室组合体连续偏航期间其本体系x轴在垂直z轴的平面内指向太阳。测量数据的天线相位中心修正首先需要计算组合体质心位置，组合体质心可参考天宫和飞船的单体质心及质量进行计算，具体如下：

r0=(mtgrtg+mszrsz)/(mtg+msz)

(1)

Δrb=Δrtg+r0

(2)

式中：r0为组合体质心位置，mtg为天宫的质量，msz为飞船的质量，rtg为天宫的质心位置，rsz为飞船的质心位置，Δrtg为接收机在组合体本体系下相对天宫质心的位置，Δrb表示导航定位接收机相对组合体质心的位置。

1.2 导航定位接收机的相位中心修正

如果在惯性系下描述距离观测量，则惯性系下的相位中心偏差为：

(3)

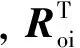
Rbo=E

(4)

然而在空间实验室连续偏航飞行姿态模式下：

SLOI=RoiSIN

(5)

Ayaw=arctan[SLOI(y)/SLOI(x)]

(6)

Rbo=Wz(Ayaw)

(7)

(8)

式中：SLOI为太阳在轨道系中的位置，SIN为太阳在惯性系中的位置，Ayaw为航天器偏航角，Wz表示绕本体系z轴旋转的矩阵，Rx表示绕本体系x轴旋转的矩阵，Rrtn表示惯性系到轨道(rtn)坐标系的转换矩阵，r表示轨道径向，t表示轨道沿迹向，n表示轨道面法向，并与r和t构成右手系，假定er，et，en分别为rtn坐标系的方向矢量，那么有：

(9)

利用式(5)和式(6)计算空间实验室连续偏航飞行过程的偏航角，计算结果如图2所示。

图2中横坐标起始时刻为2016-11-13 T 20∶00(北京时，下同)，图2(a)表示太阳与轨道面夹角变化，图2(b)表示空间实验室飞行轨道对应的偏航姿态角。

2 姿控喷气影响分析

天宫二号与神舟十一号组合体在2016-11-13 T 19∶36实施连续偏航姿态飞行，连续偏航飞行期间，天宫二号需通过连续喷气控制姿态，这个状态同时对组合体轨道产生了一定影响，下面给出了连续偏航期间(2016-11-13 T 20∶00—2016-11-14 T 08∶00)天宫二号姿控发动机喷气的数据图。

图中横坐标起始时刻为2016-11-13 T 20∶00，利用空间实验室连续偏航开始接收到的遥测喷气累计数，计算统计速度增量的结果，从遥测接收的喷气累计数为航天器本体坐标系，在定轨预报分析中需要使用的是rtn坐标系，从航天器本体坐标系至rtn坐标系的转换关系为：

ΔVb=Rb(F·Δt/M)

(10)

ΔVrtn=Rx(-90°)Rz(90°)RboΔVb

(11)

式中：F表示发动机推力，Δt表示发动机工作时间，M表示空间实验室组合体质量，Rb表示发动机安装矩阵，ΔVb表示本体系下的速度增量，ΔVrtn表示rtn坐标系的速度增量。

3 轨道动力学建模

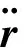
(12)

(13)

式中：ai，bi，ci(i取1，2，3)表示rtn坐标系下经验力系数，u表示组合体飞行轨道的纬度幅角。通常根据遥测计算的速度增量精度不高，加入动力学模型后对结果改善不明显，所以需要对经验力系数进行求解，得到与空间实验室连续偏航飞行轨道一致的动力学参数，进而提高定轨预报精度。

在一个测量弧段中，若需要求解多组经验力系数，可设其分别为：p1,p2,p3，…，pn，则相应的变分方程[15]表示为：

(14)

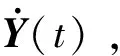
如果获得变分方程系数C(t)的表达式，同样可以进行轨道积分得到待估参数的偏导数，对于m组经验力系数q，有n=9m，且可以表示为：

q=[q1,q2, …,qm]T

(15)

其相应的C(t)可以表示为：

(16)

使用最小二乘迭代法改进计算轨道及相关的动力学参数，当本次迭代改进误差与上一次改进误差相比小于0.001 m时判定轨道收敛，得到了与动力学模型相匹配的轨道。

设置空间实验室连续偏航的定轨解算参数策略如表1所示。表1中位置速度和大气阻力系数的求解参考文献[6]。其中，m表示空间实验室测量圈数，Int()表示取整，Cd初值置为2.0。

表1 空间实验室连续偏航轨道参数求解策略Table 1 The solving strategy of orbit elements for continuous yaw mode

在经验力系数求解初值设置时，线性项使用遥测参数计算结果，周期项系数可置为0。参考表1，设置测量数据弧段为6 h，则待估参数个数为43；设置测量数据弧段为24 h，则待估参数个数为106。随着测量弧段的增加，待估参数呈等比例增加，相应地在求解高斯方程中的计算量也呈指数增加，所以在分析计算中建议测量数据弧段小于等于24 h。为提高计算灵活性可设置rtn方向求解系数可选，根据不同需求计算时可减少求解参数个数，提高求解效率。

4 轨道拟合分析

利用第3节建立的轨道动力学模型及定轨解算参数策略时，考虑到遥测计算每圈的速度增量为平均值，在式(13)中对应为线性项，解算周期项会影响其每圈拟合精度以及与遥测计算的比对统计，所以在解算姿控经验力时不解算周期项，从2016-11-13 T 20∶00起算共计27圈，解算得到的速度增量与遥测计算值统计如图4所示。

由图4可知，通过遥测计算和动力学解算两种方法计算的结果趋势基本一致，根据1个轨道周期约1.5 h推算，轨道系三个方向速度增量均存在明显的12 h演化周期。由图2可知，空间实验室在偏航角100°附近振荡变化，周期约24 h，同一周期内角度从极大值到极小值，以及从极小值到极大值两个过程中，姿控喷气对轨道的影响基本相同，特别是沿迹向和法向的速度增量在同一方向累积。通过图4计算可知，统计每圈的速度增量计算连续偏航喷气控制对轨道预报一天产生的误差在百米甚至千米量级。

根据上述情况，对组合体连续偏航期间2016-11-14 T 00∶00—2016-11-15 T 00∶00的数据进行统计定轨，分2种策略讨论分析:第1种是无姿控经验力的动力学统计定轨，求解1组Cd;第2种是修正测量数据相位中心后增加周期经验力的定轨，具体根据表1的策略计算。下面给出两种策略的定轨残差(o-c，即为观测值与定轨计算值的差)。

从图5～6可以看出，无经验力模型补偿的定轨残差为100 m，其中轨道面有较明显(米级)的系统差，该误差与连续偏航期间的导航定位接收机天线相位与质心的偏差相关，第2种策略增加相位修正和经验力补偿之后的定轨残差拟合精度明显提高，各方向位置拟合精度均小于10 m，其中轨道面(n方向)的系统差已消除。

5 定轨及预报精度分析

在精密定轨过程中解算姿控经验力设置线性项和周期项共同解算，定轨精度分析采用重叠弧段定轨星历比较进行分析，其中第1个弧段的星历范围是：2016-11-14 T 00∶00—2016-11-15 T 00∶00，第2个弧段的星历范围是：2016-11-14 T 12∶00—2016-11-15 T 12∶00，重叠弧段的范围是：2016-11-14 T 12∶00—2016-11-15 T 00∶00,时长12 h，同时将2016-11-16 T 00∶00—2016-11-17 T 00∶00和2016-11-16 T 12∶00—2016-11-17 T 12∶00作为第3和第4弧段，重叠弧段的范围是： 2016-11-16 T 12∶00—2016-11-17 T 00∶00。根据第3节分析的策略进行比较，讨论2种策略的比较精度，其中空间实验室轨道rtn坐标系下位置误差如图7所示。

图7(a)表示2016-11-14无经验力模型补偿的定轨精度；图7(b)表示2016-11-14含经验力模型补偿的定轨精度；图7(c)表示2016-11-16无经验力模型补偿的定轨精度；图7(d)表示2016-11-16含经验力模型补偿的定轨精度。将上述4类情况统计rtn坐标系各方向分量最大误差如表2所示。

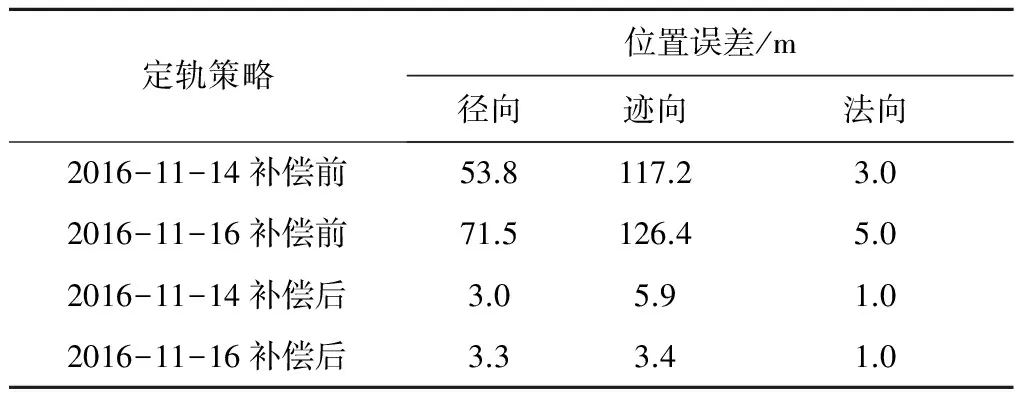
表2 空间实验室连续偏航定轨位置误差统计Table 2 Position error of overlapping arcs in continuous yaw mode

由图7和表2可知，连续偏航期间空间实验室无姿控经验力补偿的定轨精度为100 m，通过修正导航定位天线相位中心和增加周期经验力补偿后进行统计定轨的精度小于10 m，该方法比正常的定轨计算精度提高了1个数量级，该结果说明补偿后的经验力系数解算与实际一致的情况下，经验力模型能够较准确地描述姿控喷气产生的加速度影响，达到精确构建动力学模型的目的，进而提高定轨精度。

为验证该方法的正确性，使用定轨解算的结果作为先验信息，用于后续的轨道预报。在轨道预报分析时，分别利用2016-11-14 T 00∶00和2016-11-16 T 00∶00的轨道进行预报，计算时长为24 h，预报过程中分无经验力模型预报和含经验力模型补偿预报两种模式，初始历元轨道均使用精密定轨的位置速度，无经验力预报的模型参数只使用标准的一组大气阻力Cd系数(通过天宫二号伴星解算)，而含经验力补偿预报的模型参数除了使用无经验力预报的模型参数外，还增加一组起点前4圈拟合的线性经验力系数作为先验信息。将轨道预报后的星历与基准轨道进行比较(基准轨道采用精密定轨得到的星历)，计算结果如图8所示。

图8(a)表示2016-11-14无经验力模型补偿的预报误差；图8(b)表示2016-11-14含经验力模型补偿的预报误差；图8(c)表示2016-11-16无经验力模型补偿的预报误差；图8(d)表示2016-11-16含经验力模型补偿的预报误差。将上述4类情况统计rtn坐标系各方向分量最大误差如表3所示。

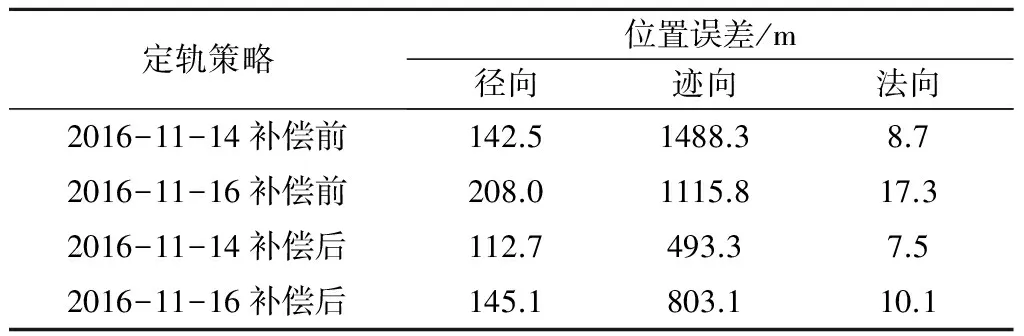
表3 空间实验室连续偏航轨道预报位置误差统计Table 3 Orbit prediction error of overlapping arcs in continuous yaw mode

由图8和表3可知，连续偏航期间空间实验室喷气控制姿态对轨道预报的影响较大，正常无经验力模型预报24 h误差大于1 km，误差主要体现在沿迹方向，通过含先验经验力参数的动力学模型预报精度提高至百米量级，迹向误差比无经验力信息预报的误差减小了1倍，该结果说明前期定轨解算得到的姿控喷气先验信息可以应用于后续轨道预报的动力学模型补偿中，虽然预报模型参数不能完全准确描述该时段的周期变化状态，但是在姿控喷气的系统误差及加速度影响上与实际基本一致，使得补偿后的动力学模型比补偿前的更加精确，提高了连续偏航的轨道预报精度。

6 结 论

本文根据空间实验室组合体连续偏航的特点，建立了相对应的测轨数据相位中心修正算法和轨道动力学模型，其中姿控喷气利用经验力模型求解线性项和周期项，在定轨计算中，设计了多参数联合求解的策略，解算速度增量与空间实验室遥测计算值一致，同时将空间实验室在连续偏航期间的定轨精度从百米级误差提高到十米以内，在连续偏航期间轨道预报中增加了先验经验力信息后将预报精度从千米量级提高到了百米量级，轨道预报精度提高了1倍。本文设计的测量数据修正算法和轨道动力学模型对于后续空间实验室天宫二号与天舟一号组合飞行以及我国的载人空间站飞行均能提供高精度轨道支持。

[1] 张柏楠, 马晓兵, 郑伟, 等. 中国载人交会对接技术的设计与实现[J]. 中国科学:技术科学, 2014, 44(1):1-11. [Zhang Bai-nan, Ma Xiao-bing, Zheng Wei, et al. Design and implementation of China’s manned rendezvous and docking tech-nology [J]. Scientia Sinaca Technologica, 2014, 44(1): 1-11.]

[2] 杨震, 刘俊泽, 王航, 等. 轨道舱偏航机动飞行实测数据分析[J]. 载人航天, 2004,3:50-54. [Yang Zhen, Liu Jun-ze, Wang Hang, et al. The flight measured data analysis of orbital module in yaw maneuver [J]. Manned Spaceflight, 2004, 3: 50-54.]

[3] 帅青松. 长期低轨航天器偏航机动飞行对其轨道影响[J]. 载人航天, 2003, 2:44-47. [Shuai Qing-song. The influence of long term LEO spacecraft yaw flight on its orbit [J]. Manned Spaceflight, 2003, 2: 44-47.]

[4] 陈建荣, 王家松. 磁暴下的LEO卫星精密轨道确定[J]. 飞行器测控学报, 2005, 24(6):34-38. [Chen Jian-rong, Wang Jia-song. Precision orbit determination of low-earth orbiters under magnetic storms [J]. Journal of Spacecraft TT & C Technology, 2005, 24(6): 34-38.]

[5] 朱战霞, 裴韶彬, 唐歌实. 一种航天器有效迎风面积的求解方法[J]. 飞行力学, 2014, 32(3):231-234. [Zhu Zhan-xia, Pei Shao-bin, Tang Ge-shi. An algorithm for solving the effective front face area of spacecraft [J]. Flight Dynamics, 2014, 32(3): 231-234.]

[6] 张宇, 段建锋, 陈明, 等. 一种提高空间实验室定轨预报精度的方法[J]. 宇航学报, 2016, 37(9): 1056-1062. [Zhang Yu, Duan Jian-feng, Chen Ming, et al. A method for improving the accuracy of space laboratory orbit determination [J]. Journal of Astronautics, 2016, 37(9): 1056-1062.]

[7] 苍中亚, 薛炳森, 程国生, 等. 大气阻力参数修正对低轨空间目标轨道预报精度的改进[J]. 空间科学学报, 2016, 36(2):188-195. [Cang Zhong-ya, Xue Bing-sen, Cheng Guo-sheng, et al. Atmospheric drag coefficient modification for orbit prediction precision improvement of LEO space objects [J]. Chin. J. Space Sci., 2016, 36(2): 188-195.]

[8] 赵长印, 吴连大. 变阻力大气摄动问题[J]. 天文学报, 1996, 37(1):91-96. [Zhao Chang-yin, Wu Lian-da. The problem of variable air drag perturbation [J]. Acta Astronomica Sinica, 1996, 37(1): 91-96.]

[9] 裴韶彬. 近地航天器大气阻力精细建模研究 [D]. 西安: 西北工业大学, 2013. [Pei Shao-bin. Study on the fine modeling of atmospheric drag in LEO spacecraft [D]. Xi’an: North Wes-tern Polytechnical University, 2013.]

[10] 刘卫, 王荣兰, 刘四清. 基于小波变换的卫星阻力系数分析[J]. 宇航学报, 2015, 36(2):142-150. [Liu Wei, Wang Rong-lan , Liu Si-qing. Analysis of satellite drag coefficient based on wavelet transformation [J]. Journal of Astronautics, 2015, 36(2): 142-150.]

[11] 刘舒莳, 龚建村, 刘四清. 中长期轨道预报中大气阻力系数补偿算法的研究[J]. 宇航学报, 2013, 34(2):157-162. [Liu Shu-shi, Gong Jian-cun , Liu Si-qing. Atmospheric drag coefficient calibration in medium-term orbit prediction [J]. Journal of Astronautics, 2013, 34(2): 157-162.]

[12] Doornbos E, Klinkrad H, Visser P. Atmospheric density calibration using satellite drag observations [J]. Advances in Space Research, 2005, 36(3): 515-521.

[13] Doornbos E, Klinkrad H, Visser P. Use of two-line element data for thermosphere neutral density model calibration [J]. Advances in Space Research, 2008, 41(7): 1115-1122.

[14] 张宇, 陈明, 段建锋, 等. 轨道机动模型在低轨航天器定轨中的应用研究[J]. 载人航天, 2013, 19(4): 45-51. [Zhang Yu, Chen Ming, Duan Jian-feng, et al. Orbit maneuver model application in spacecraft orbit determination [J]. Manned Spaceflight, 2013, 19(4): 45-51.]

[15] 张宇, 曹建峰, 段建锋, 等. 嫦娥三号探测器连续姿控的轨道动力学模型补偿及实现[J]. 宇航学报, 2015, 36(5): 489-495. [Zhang Yu, Cao Jian-feng, Duan Jian-feng, et al. Orbit dynamics model compensation and implementation for continuous control of Chang’e 3 probe [J]. Journal of Astronautics, 2015, 36(5): 489-495.]

[16] 李济生.人造卫星精密轨道确定[M].北京：解放军出版社,1995.

AnalysisandModelingofSpaceLaboratoryOrbitunderContinuousAttitudeControlPerturbation

ZHANG Yu, ZHOU Li, KONG Jing, HAN Yi, DUAN Cheng-lin

(Beijing Aerospace Flight Control Center, Beijing 100094, China)

For a space laboratory in continuous yaw mode, the influence of the continuous attitude control on its orbit is analyzed and the phase correction algorithm of a large-scale spacecraft is proposed; besides, the empirical force compensation model is established to solve the precise orbit determination of the space laboratory in continuous yaw mode. Then the influence factor of the attitude control jet in continuous yaw mode is analyzed. The velocity increment in the orbital coordinate system of each circle is less than 1cm/s, and the order of magnitude and tendency of the result of the orbit solution conforms with the telemetry measurement. Finally, the orbit determination accuracies before and after precise modeling are compared, the orbit determination accuracy with empirical force compensation model is better than 10 m, and orbit prediction accuracy for 1 day has been improved doubly.

Space laboratory; Continuous yaw; Attitude control jet; Precise orbit determination; Orbit dynamics; Model compensation; Phase correction

2017- 03- 14;

2017- 09- 26

国家自然科学基金(61573049, 11373013)

V412.4

A

1000-1328(2017)12- 1273- 08

10.3873/j.issn.1000- 1328.2017.12.003

张宇(1979-)，男，硕士，主要从事航天器测定轨技术方面的研究。

通信地址：北京5130信箱(100094)

电话：(010)66361456

E-mail:zackyzy@163.com