基准剂量估计的非参数贝叶斯方法研究与应用*
2018-01-03顾彩姣
顾彩姣 王 涛 王 彤
基准剂量估计的非参数贝叶斯方法研究与应用*
顾彩姣1,2王 涛2王 彤1△
目的比较两种基准剂量估计的非参数贝叶斯方法在不同剂量反应数据情形下的表现,再与参数模型作比较。方法介绍基于加权过程和随机过程的非参数贝叶斯方法的基本原理,通过模拟分析与实例研究比较各方法结果的差异。结果模拟研究显示,两种非参数方法NPB1和NPB2的估计结果都与真实BMD值较为接近,NPB2方法的BMDL覆盖率更接近真实水平,因此更为可取;实例中与参数模型结果相比,非参数方法得到的BMD估计值都落入或非常接近由参数模型得到的BMD估计值的范围,而非参数方法估计的BMDLs值大多比参数模型算得的BMDLs值要小。结论两种非参数贝叶斯方法都可提供合理的拟合值,尤其是在传统的参数模型无法得到拟合结果的情况下,也可很好的应用;NPB2方法在估计结果和软件运算速度方面均略优于NPB1。
基准剂量 BMDS软件 非参数方法 狄利克雷分布 布朗运动
过去几十年一直采用未观察到有害作用剂量(no-observed-adverse-effect-level,NOAEL)来评估非致癌物的健康风险[1]。但这种方法的使用依赖于大量定义好的限制条件,比如剂量选择、剂量间隔、在选定剂量水平时使用的动物数量等,且该方法也未考虑剂量反应曲线的形状等信息。因此,科学家们开始探索其替代方法。基准剂量法(Benchmark Dose,BMD)是由美国科学家Crump于1984年最先提出的[2],该方法提出后引起了科学家们的广泛关注,并将大量历史资料进行了运算验证,他们认为BMD弥补了NOAEL的不足之处。基准剂量方法也被用在发育毒物以及神经毒物终点事件研究中,很多文献认为基准剂量法在毒理学中的应用已经多于其在风险评估中的应用了[3-5]。
目前文献研究中基准剂量的估计方法主要有:针对不同类型反应数据的参数模型;模型平均法;半参数方法和非参数方法等。参数模型在使用中需进行模型选择,因此存在不确定性[6-7];模型选择法是在一定模型空间内将不确定性移除,但未克服不确定性[7];形式较为灵活的半参数方法和非参数方法近年来使用较多,半参数方法计算复杂[8-9],因此本文主要研究非参数方法[10]。
原理与方法
1.基准剂量
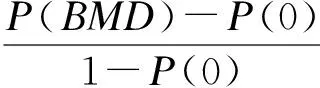
2.基于加权过程的非参数贝叶斯方法[12](NPB1)
该方法的主要思想是将反应概率函数p(d)定义为关于d的光滑、单调非减、取值范围在0到1之间的函数,即:
(1)
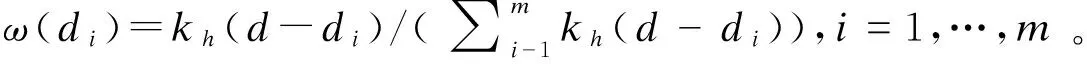

πΔ(Δ)=Dirichlet(α1,…,αm+1)
(2)
本文中超参数α1,…,αm+1指定为(1,1,…,1)/(m+1)。
在贝叶斯方法里,宽度参数h是未知的,可指定一个先验信息。在将剂量水平标化为单位区间后,假定宽度参数小于1,并使用Beta分布:
πh(h)=Beta(α,β)。
(3)
将反应率记为p(d;Δ,h),表明概率值对参数Δ和h的依赖性。此时参数估计的似然函数为:
(4)
π(Δ,h|y1,…,ym)∝L(Δ,h|y1,…,
ym)πΔ(Δ)πh(h)
(5)
其中ni为每个剂量下的实验动物数,yi为每个剂量组内结局为阳性反应的动物数。为采用MARKOV CHAIN MONTE CARLO(MCMC)方法从后验信息中抽样,标准的Metropolis-Hastings 算法可从近似的后验中得到大量的L样本。令(Δ(1),h(1)),…,(Δ(L),h(L))为后验信息中抽出的L个样本。由这些后验样本可得到全部的后验曲线p(d;Δ(l),h(l)),l=1,…,L,剂量反应关系的后验估计为:
(6)
贝叶斯方法的有用之处在于后验样本可提供所有重要未知量的推断,未知量
BMD(l)=BMD(p(d,Δ(l)),h(l),γ),l=1,…,L
(7)
BMD可由后验估计均值得到:
(8)
3.基于随机过程的非参数贝叶斯方法[12](NPB2)
该方法假定剂量反应关系是由基于d的随机过程得到的,该随机过程需确保每个样本都满足光滑、单调递增,p(d)取值范围在0到1之间的一般特征。本文使用的方法是由一种特殊的高斯过程-布朗运动(brownian motion, BM)得到的。
假定ω(d)是关于d的标准布朗运动,则有ω(d1)=0,且当di (9) 整合的BM形式已经被用在二分回归问题的非参数贝叶斯建模过程中,近年来研究者们也都探讨过整合指数BM方法的一些性质。整合随机过程的指数形式为递增的非负函数,也已被用在了光滑单调回归方法中。 剂量反应关系的模型为: p(d)=p0+(1-p0)z(d) (10) 对照组的反应率应满足0≤p0=p(0)≤1,为了保持范围限制,如0≤p(d)≤1,我们将BM的形式截取为: (11) 为实现该方法,我们使用离散的BM形式,给定增量ω(dj)-ω(dj-1),j=1,…,m。则整合的指数BM的形式近似为: (12) 对于每个j,ω(xj)-ω(xj-1)~N(0,λ(xj-xj-1)),λ为方差参数。同时,假定基线反应p0的先验分布为Beta(a,b),此时,似然和先验相互独立,为: (13) 之后BMD和BMDL值的估计方法与NPB1类似。 1.模拟数据设置 假定多阶段模型为真实的剂量反应关系,模型包含四个参数q=(q0,q1,q2,q3),剂量反应函数为p(d)=1-exp(-q0-q1d-q2d2-q3d3),该多阶段模型用MS(q0,q1,q2,q3)来表示。假定每个剂量点di的动物数均为ni=50,剂量反应数据服从二项分布B(ni,p(di))。在使用贝叶斯方法时,设定MCMC抽样的N=10000,B=5000;NPB1方法中每个样本的宽度参数h均使用beta(0.7,1),而狄利克雷参数α1,α2,…,αm+1为(1,1,…,1)/(m+1);NPB2中,假定p0的先验为beta(0.1,1),方差参数λ取0.0001。在函数p的表达式已知,额外风险设置为10%的情况下,我们可以计算得到每种数据下的真实的BMD值。 参照其他文献研究[13],本模拟设定两种不同的参数配置,分别为:q=(0,1,1,3)和q=(0.05,0,3,0);剂量组数m=4和m=6两种情况;剂量设置为等间距和近似对数间距两种情况。以上参数设置构成8种不同情形的剂量反应数据,在每种情况下,都产生R=500的独立蒙特卡洛样本,每个样本都用NPB1,NPB2两种方法估计,以BMD估计值与真实值的差距以及BMDL的覆盖率为评价指标,比较这两种方法在不同剂量反应数据情形下的表现。BMDL的覆盖率是由R个估计值中,包含了真实BMD值的100(1-α)%可信区间所占的比例得到。我们分别取α=0.10和0.05,得到对应的90%和95%可信区间覆盖率。 表1 模拟研究结果 2.模拟结果 由表1中的结果可以看到, NPB1和NPB2两种方法得到的BMD后验估计均值都与真实BMD值较为接近。当多阶段模型参数设置为MS(0,1,1,3)、剂量组数为6,间距为对数时,NPB1方法的覆盖率明显低于正常水平,表明此时的BMD估计值有较大偏倚。而NPB2方法的覆盖率更接近真实水平,且运算速度较快,模拟一次的时间是NPB1方法的1/10左右,就本次研究来讲,NPB2方法较NPB1方法更为可取。 1.实例数据来源 从Nitcheva等人2007年分析过的数据集中,选取9组癌症数据进行分析[14]。 表2 选自Nitcheva et al.(2007)的9组癌症数据实例 2.实例分析结果 对于每个数据集,都采用BMDS软件中包含的9种二分反应模型[15],以及NPB1和NPB2分别来估计剂量反应关系,BMD和BMDL值见表3。 表3 参数方法与非参数方法估计结果的比较 表3中是两种非参数方法和BMDS软件模型包中参数模型的估计结果。BMDS软件的结果包括两部分:由AIC值最小原则选出的最优参数模型的估计结果;满足模型拟合优度检验界值的所有参数模型估计出的BMDs和BMDLs的范围。9组实例由两种非参数方法得到的估计结果比较接近,而NPB2方法的估计值略低于NPB1方法得到的估计值。而两种非参数方法的BMD估计值大多都在实验剂量范围之内,而已有证据都表明在这个范围内可以观察到10%的额外风险发生。 与不同的参数模型结果相比,两种非参数方法得到的BMD估计值都落入或非常接近由参数模型得到的BMD估计值的范围;而在可信区间方面,非参数方法估计的BMDLs值大多比参数模型算得的BMDLs值要小,这很可能是因为非参数方法考虑的功能空间更大。对于某些剂量反应数据类型,在常用的参数模型无法给出合理拟合值的情况下,非参数方法仍可较好的使用,这也充分说明了非参数方法在其使用中的灵活性和应用范围的广泛性。 在拟合毒理实验动物数据的剂量反应曲线时,使用参数模型通常要根据AIC最小原则进行模型选择。Webster等人2012年的一篇文章对BMD估计中模型不确定性及其影响做了详细研究。模拟研究表明[16],当每组剂量实验动物数比较少(低于50)时,通过AIC原则选出正确模型的概率均明显很低,且模型包含的参数越多,每组动物数越少,被选为正确模型的概率越低;当样本量增加时,该概率值会升高,但样本大小为1000时,选出正确模型的概率最高也只能达到77%。另外,通过最优模型计算得到的BMDL值与指定的真实模型的BMD值的比较发现,BMDL值低于BMD值的概率值远低于理想水平95%。一旦模型指定错误,它估计的BMDL值便会大于选定的BMR值,通常会超出6倍以上。在实际的风险评估过程中,这种超出率被认为是无法接受的。 非参数方法在进行剂量反应曲线拟合过程中的使用非常灵活,在某些数据情形下参数模型无法使用,非参数方法依然可以得到很好的估计值,并且解决了模型不确定性的问题,作为目前可用的参数模型的补充与替代方法,有很重要的意义和使用价值。常用的非参数方法有多种,如分位数回归,保序回归,非参数贝叶斯方法等。分位数回归在实验剂量点较少时,通常估计偏倚较大;保序回归BMDL的覆盖率也比贝叶斯方法的低;而非参数贝叶斯方法可通过指定先验来合并一些背景信息,尤其是在剂量点较少时,该特点让非参数贝叶斯方法应用更广。 在实际应用中,当样本量很大(N=1000)时相应的模型选择的正确率较高,可根据参数模型估计相应的BMD和BMDL值,但BMDS软件中包含的参数模型较多,需要用各个模型分别拟合数据,后根据模型拟合优度检验结果及AIC原则等模型选择方法选出最优模型,整个计算过程比较繁琐,还要承担模型错误指定的风险,因此,推荐使用本课题提到的非参数贝叶斯方法。虽然两非参数贝叶斯方法原理部分较难理解,但其相应的R程序均已编写完成,使得应用非常方便、省时,结果却更加保守可靠。而NPB2方法与NPB1方法相比,在拟合结果精度和软件运算速度方面优势更明显,更推荐NPB2方法。 [1] Davis JA,Gift JS,Zhao QJ.Introduction to benchmark dose methods and U.S.EPA′s benchmark dose software(BMDS)version 2.1.1..Toxicology and Applied Pharmacology,2011,254:181-191. [2] Crump KS.A new method for determining allowable daily intakes.Fundamental and Applied Toxicology,1984,4:854-871. [3] European Chemicals Bureau(ECB).Technical guidance document on risk assessment of chemical substances following european regulations and directives,parts i-iv.http://europa.eu.int,2016-03-20. [4] U.S.General Accounting Office.Selected federal agencies′ procedures,assumptions,and policies.Washington,2001-08:64-151. [5] OECD.Current approaches in the statistical analysis of ecotoxicity data:A guidance to application.Environment Directorate,Organisation For Economic Co-Operation and Development.www.univet.hu,2006. [6] Faustman EM,Bartell SM.Review of noncancer risk assessment:Applications of benchmark dose methods.Hum.Ecol.Risk Assess,1997,3(5):893-920. [7] Kang SH,Kodell RL,Chen JJ.Incorporating model uncertainties along with data uncertainties in microbial risk assessment.Regul.Toxicol.Pharmacol,2000,32(1):68-72. [8] Wheeler MW,Bailer AJ.Monotonic Bayesian Semiparametric Benchmark.Risk Analysis,2012,32(7):1207-1218. [9] Bosch RJ,Wypij D,Ryan LM.A semiparametric approach to risk assessment for quantitative outcomes.Risk Analysis,1996,16(5):657-665. [10]Bhattacharya R,Lin L.Nonparametric benchmark analysis in risk assessment_ A Comparative study by simulation and data analysis.Statistics and Probability Letters,2010,80:1947-1953. [11]张俊杰,张海燕.基准剂量评估系统的研究与实现.北京林业大学,2013:1-45. [12]Guha G,Roy A,Kopylev L,et al.White P.Nonparametric Bayesian Methods for Benchmark Dose Estimation.Risk Analysis,2013,33(9):1608-1619. [13]Kopylev L,Fox J.Parameters of a Dose-Response Model Areon the Boundary:What Happens with BMDL.Risk Analysis,2009,29(1):18-25. [14]Nitcheva DK,Piegorsch WW,West RW.On use of the multistage dose-response model for assessing laboratory animal.Regulatory.Toxicology and Pharmacology,2007,48:135-147. [15]顾刘金,陈琼姜,吴立仁,等.基准剂量统计软件BMDS简介.中国卫生统计,2005,22(4):257-258. TheStudyandApplicationofNonparametricBayesianMethodsforBenchmarkDoseEstimation Gu Caijiao,Wang Tao,Wang Tong (DepartmentofHealthStatistics,ShanxiMedicalUniversity(030001),Shanxi) ObjectiveComparing the performance of the two nonparametric Bayesian methods for benchmark dose estimating under different dose response data,then comparing them with traditional parametric methods.MethodsIntroduce the basic principle of the nonparametric Bayesian method based on weighted process and stochastic process separately,then compared the estimations through simulate study and instance analysis.ResultsThe simulate study shows that the posterior estimates were reasonably close to the target true BMD value for the two nonparametric methods,and NBP2 is more desirable compared to NPB1.The nine examples indicate that the BMD estimates from the nonparametric approaches generally fall into or very near the interval of those obtained from BMDS and nonparametric approaches tend to produce lower BMDLs than the parametric modeling approaches.ConclusionThe posterior estimates were reasonably close to the target true BMD value for the two nonparametric methods,especially when standard parametric models fail to fit to the data adequately.The NPB2 method is slightly bet-ter than the NPB1 method in the aspect of estimation result and the software operation speed. Benchmark dose;BMDS software;Nonparametric method;Dirichlet distribution;Brownian motion 国家自然科学基金(81473073) 1.山西医科大学卫生统计教研室(030001) 2.海淀区东升镇社区卫生服务中心预防保健科 △通信作者:王彤,E-mail:wtstat1@sina.com 郭海强)
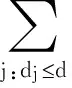
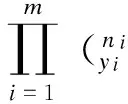
模拟研究

实例分析

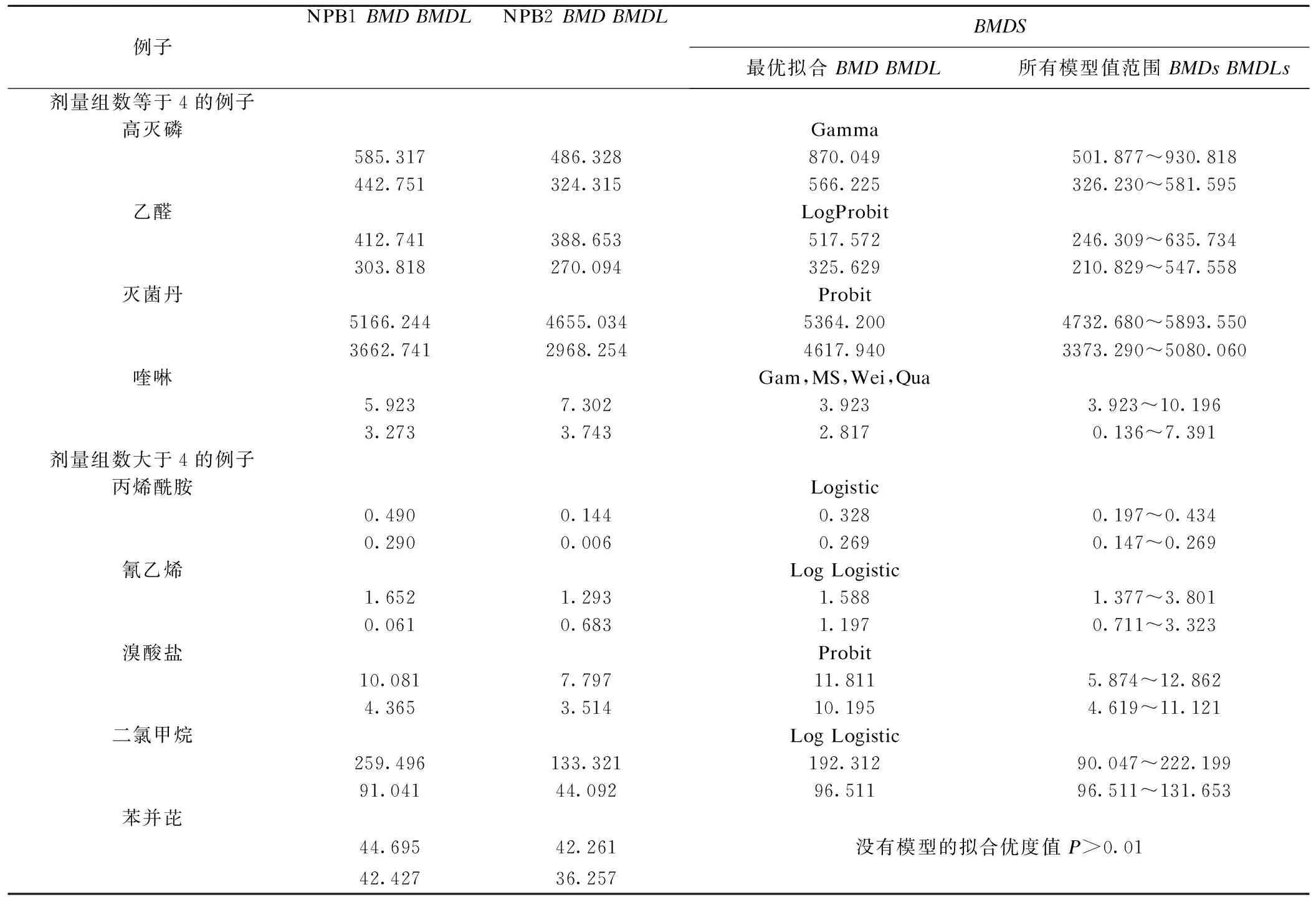
讨 论
