一类传输问题的自适应FEM-BEM方法

王娜，邱亚南，刘东杰

（上海大学 理学院，上海 200444）

0 引言

设Ω为具有Lipschitz 边界Γ的单连通的有界区域，Ωc：=R2/Ω为其外部区域，对于给定的函数f∈L2(Ω)，u0∈H1/2(Γ)，t0∈H－1/2(Γ)，考察如下的界面传输问题：求(u，uc)∈H1(Ω) ×H1(Ωc)满足

其中，b∈R是有界常数，n是边界上由内部Ω指向Ωc的法向量。本文采用Sobolev 空间中的常用记号［1］，Sobolev 空间Wm，2(Ω)简记为Hm(Ω)，||·||Hm(Ω)和|·|Hm(Ω)分别表示Hm(Ω)空间中的范数和半范数。Hm(Ω)（m是整数）的迹空间记为Hm－1/2(Γ)，迹算子γ：Hs(Ω) →Hs－1/2(Γ)，u|Γ：=γu。A≲B表示存在常数C使得A≤CB。∀v∈H1(Ω)，定义能量范数的形式如下：

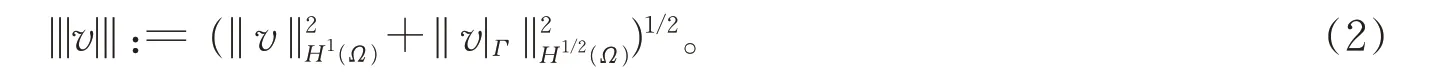
对于上述界面问题的求解有很多不同的耦合方法［2-3］，而由冯康和余德浩教授提出的自然边界元与有限元方法是基于相同的变分原理，可以自然而直接的耦合［4］。该耦合法的刚度矩阵就是有限元和边界元的矩阵之和，相比有限元与古典边界元耦合法的计算更加简单［5-6］。 采用均匀剖分的自然边界元与有限元的耦合法已经得到一定的应用［7］，文献［8-9］分别利用非匹配网格和最速下降法给出在均匀剖分下该问题的数值解。

对于有奇异性的问题，均匀剖分比较浪费资源，而近些年比较流行的自适应技术是处理大梯度和有间断解问题的有效工具。自适应技术在有限元与古典边界元耦合中的应用已经比较成熟，其关键是找到合适的后验误差估计指导局部网格细化过程，从而使数值解更快地逼近真实解，例如：

·h-h/2 后验误差：此后验误差估计独立于问题，节省开销从而备受关注。对于有限元问题，边界元问题以及耦合问题，基于h-h/2 后验误差估计的自适应算法在饱和性假设的条件下都被证明是收敛的［10-11］。

·二水平后验误差估计：Mund 等［12］利用层次基技术给出二水平后验误差估计，此后验误差估计方便边界元和有限元实施独立的细化，后来Kerb 结合Steklov-Poincare 算子将二水平后验误差估计作为局部误差指示因子来研究自适应有限元与边界元耦合［13］。

·基于残差的后验误差估计：Carstensen 等［14］运用自适应有限元与古典边界元耦合法求解界面问题时，导出了一个基于残差的后验误差估计给出了误差的一个上界。

对于线性界面传输问题，h-h/2 后验误差估计等价于二水平后验误差估计［11］。Feischl 等［15］针对界面传输问题分别讨论基于二水平后验误差估计和基于残差的后验误差估计并分析了自适应过程的收敛率，文献［16］给出两种后验误差估计的可靠性和有效性分析。

综上，关于自适应有限元与古典边界元耦合已有较多的研究成果，而关于自适应自然边界元的耦合研究较少，本文利用自然边界元的良好性质，研究自适应有限元与自然边界元耦合法。为了叙述和计算的方便，我们考虑Ω为圆域的线性界面传输问题（1）的自适应有限元与自然边界元耦合法。具体框架如下：第一部分给出了等价的变分问题；第二部分给出离散的变分问题；第三部分给出本文的两个误差分析，即h-h/2后验误差估计和基于残差的后验误差估计；最后利用数值算例验证我们的理论结果。

1 变分问题

针对半径为R的圆外区域问题，引入自然积分算子K：H1/2(Γ) →H－1/2(Γ)和泊松积分算子P：H1/2(Γ) →H1(Ω)［5］，则泊松积分方程和自然积分方程如下所示，* 号是指自然积分算子K 作用于函数u0，

设(u，uc)是方程（1）的解，对方程（1）的第一个表达式两边同乘v∈H1(Ω)，应用Green 公式可得

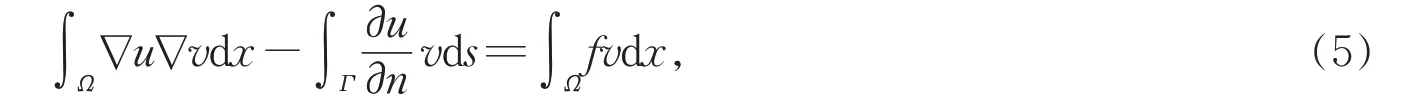
将方程（1）的第5 个表达式代入（5）式得

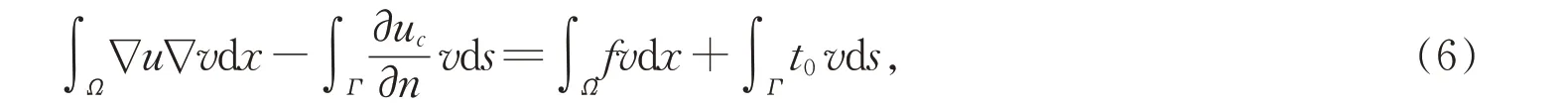
由方程（1）的第二个式子和第四个式子可得如下的自然积分方程和泊松积分方程，

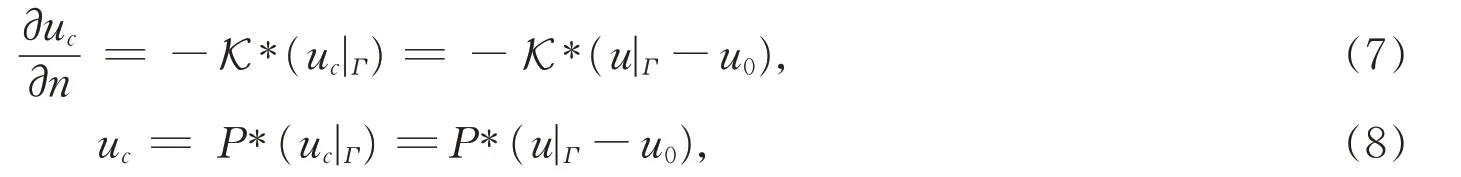
利用自然积分算子K 的双线性，将（7）式代入（6）中得到，

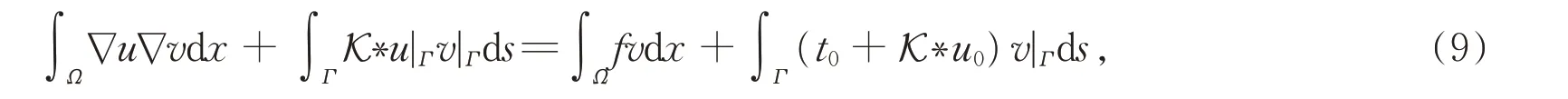
也即(u，uc) ∈H1(Ω) ×H1(Ωc)满足如下的变分问题，

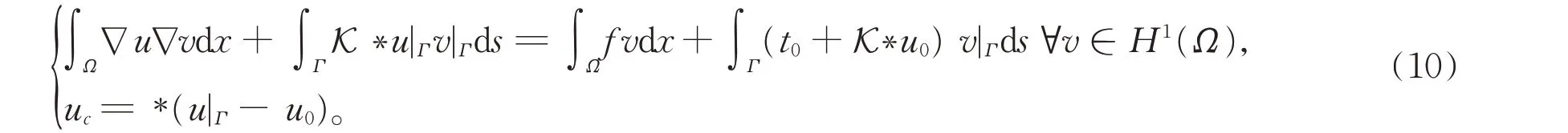
因此，变分问题（10）等价于微分方程（1）。显然，求解变分问题时，只需求出u∈H1(Ω)即可，而uc依赖于u|Γ利用（10）的第二个表达式可以求出。

我们定义算子A(u，v) ：H1(Ω) ×H1(Ω) →R和线性泛函L(v) ：H1(Ω) →R的表达式如下：

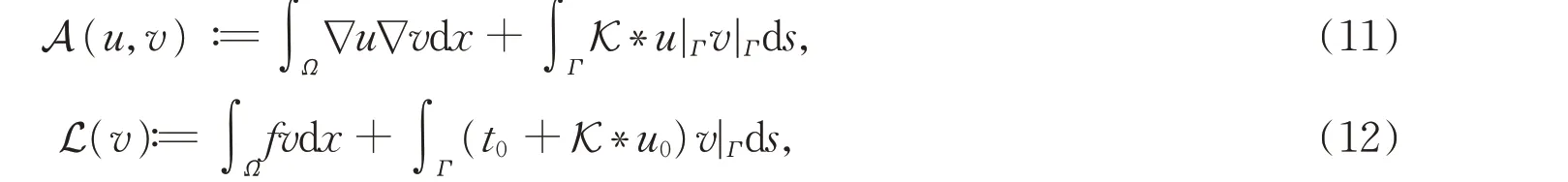
则变分问题（10）等价于下述方程，

由商空间中的等价模定理可知［1］，存在常数C，使得对∀u∈H1(Ω)/P0，

因此，双线性型A(u，u) 也是V-椭圆的，存在常数C使得

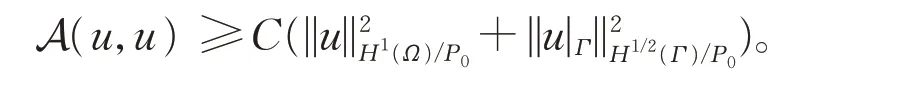
又因为双线性型A(u，u) 是连续的［4］，由Lax-Milgram 定理可得，变分问题（13）在商空间H1(Ω) /P0中存在唯一解。

2 离散变分问题

设Th是区域Ω的拟正则三角剖分，Th/2是对Th的一致细化得到的网格剖分，Th+1是对Th实施一次自适应加密细化后得到的新一层网格剖分。Eh表示剖分三角单元所有边的集合，Eh(Ω)和Eh(Γ)分别为内部和边界上的边的集合。N 记为剖分节点集合，N (Ω)和N (Γ)分别表示区域内和边界上所有节点的集合，n1，n2分别为集合N (Ω)，N (Γ)中元素的个数。对于任意的三角单元T∈Th，hT∶= diam(T)，Eh(T)是单元T的三边的集合，对任意的边界单元E∈Eh，hE∶= diam(E)，hΓ∶= maxE∈Eh(hE)，hΓ≈hE≈hT≈|T|1/2。

为了便于实施，令边界的剖分与区域的三角剖分在边界上是一致的。原问题（13）的离散变分形式如下：

3 后验误差估计

后验误差主要利用数值解和已知条件估计真实解和数值解的误差大小。对于我们研究的线性问题，h－h/2 后验误差估计和二水平后验误差估计是等价的［10］，因此本节主要研究h－h/2 法和残差法这两个主流的后验误差估计。

3.1 h－h/2后验误差估计

本节主要在有限元与自然边界元的耦合框架下利用h－h/2 后验误差估计的思想给出与误差的能量范数|||u－uh|||等价的估计量ηl和μl

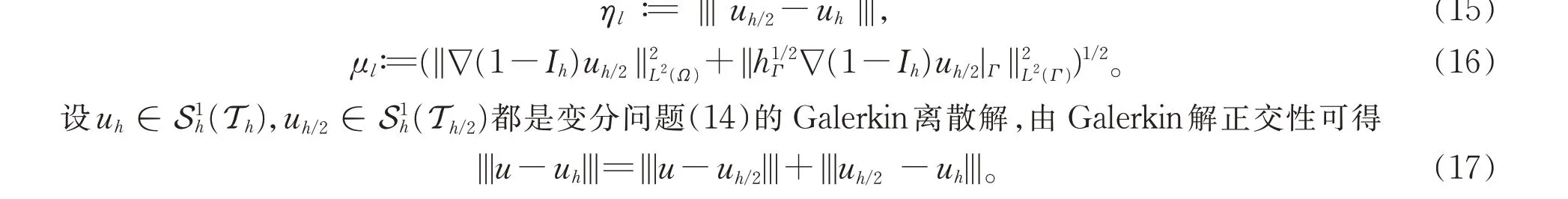
令数值解满足饱和性假设条件：

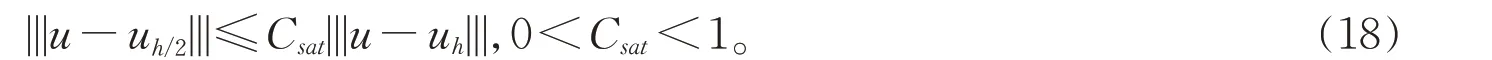
由（17）式和（18）式易得，存在常数C使得后验误差估计量ηl和误差|||u－uh||| 满足下述关系

存在常数C∞＞0 使得∀T∈Th，

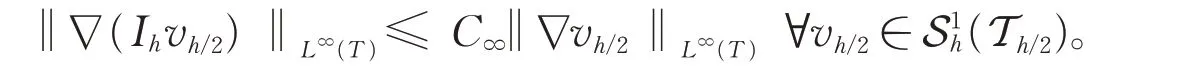
那么利用上面两个式子可得

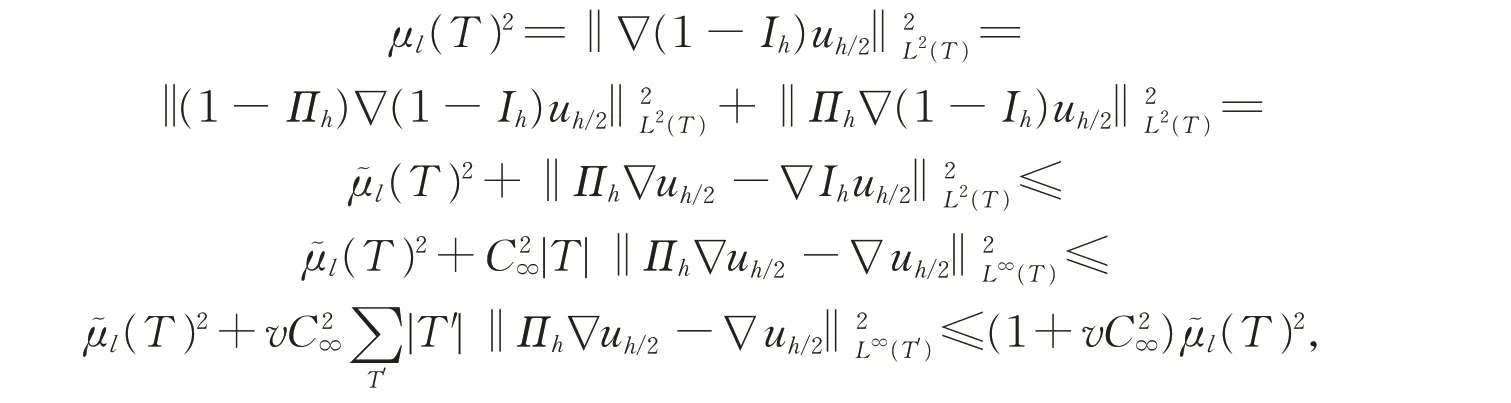
其中，T′ ∈Th/2是一致细化Th中的三角单元T得到的任一子单元，且有|T| ≤v|T′|，v为常数。

定理1 在饱和性假设的条件下，存在常数C1，C2＞0，使得

由Glerkin 解的拟最优性可知

由文献［18］引理2.2 可得，

由最后两个估计式（24）式和（25）式得ηl≲μl。

综上可得，μl≲ηl≲μl，结合（19）式可得

因此，μl是误差|||u－uh|||的有效且可靠的后验误差估计量。

3.2 基于残差的后验误差估计

本节主要利用自然积分算子的性质，推导出一个形式较为简单且易于计算的后验误差估计。

其中ηh(T)的表达式如下：

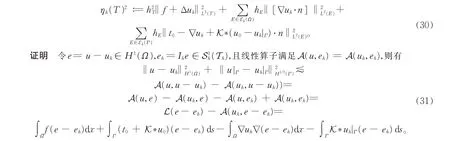
令[∇uh·n]表示uh在单元的边界E上法向导数的跃度，对区域Ω每个元素T∈Th上应用Green 公式可得，

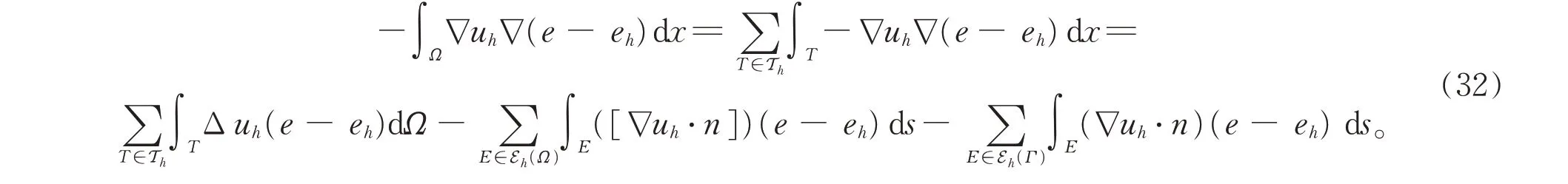
将（32）式代入（31）式可得

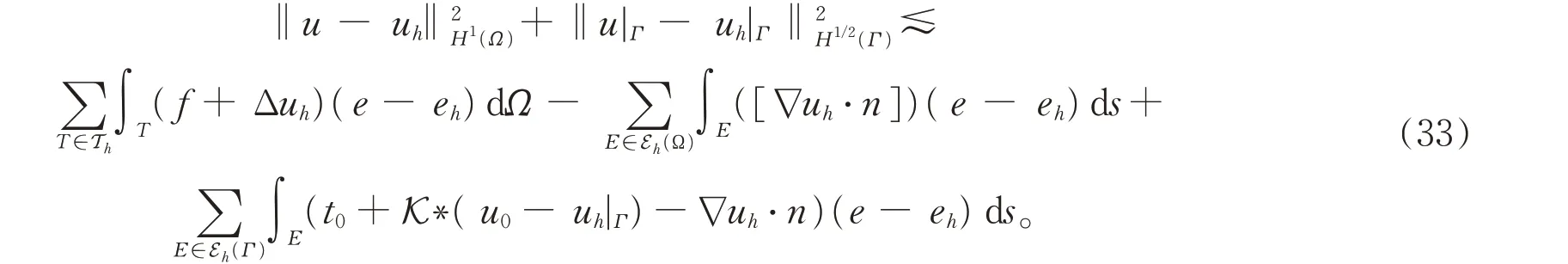
由Ho¨lder 不 等 式 和 引 理1 可 得，

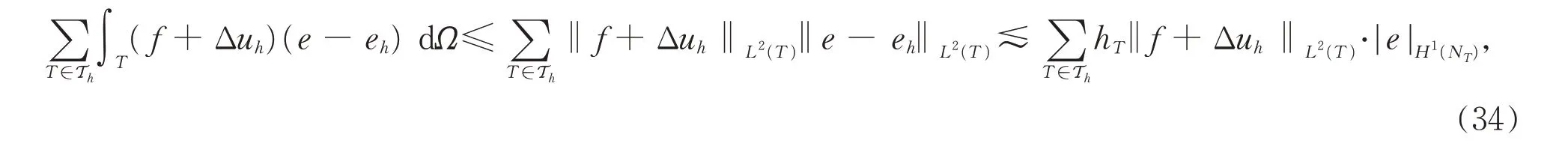
再利用Cauchy 不等式可得

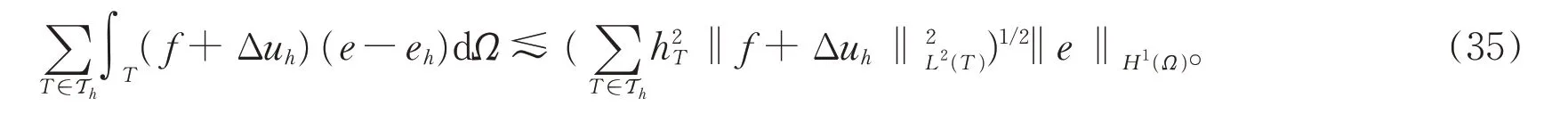
结合引理1 和引理2 可得对任意三角单元T的边E∈Eh有下述不等式成立，

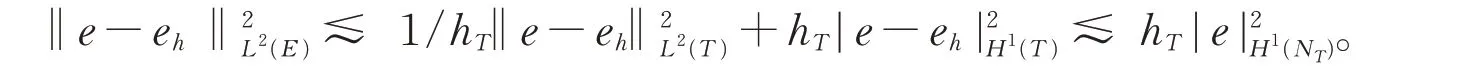
从而可得（33）式右端第二项和第三项有如下估计，

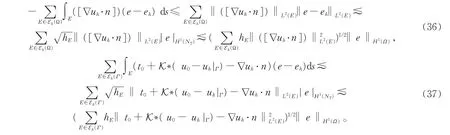
将以上不等式（35）－（37）代入（33）式可得

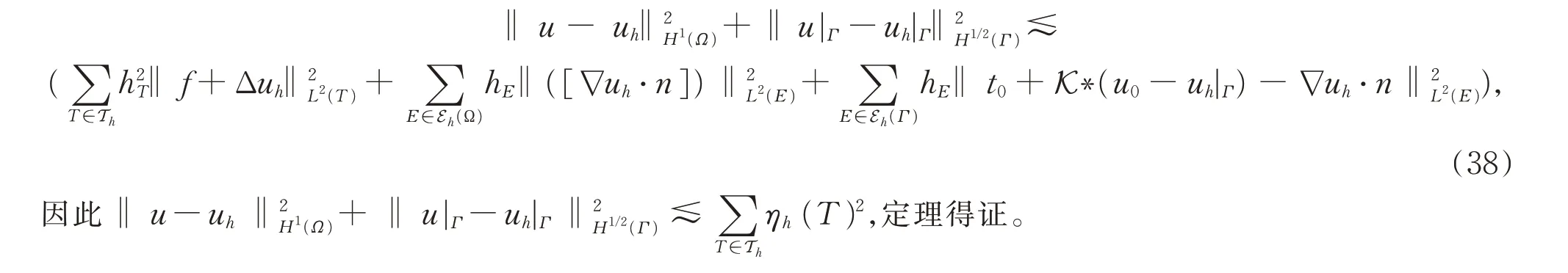
4 数值实验

本节主要利用上面给出的两个后验误差估计进行自适应有限元与自然边界元耦合的数值实验。自适应流程如下：

输入：初始网格，自适应细化参数θ∈(0，1)

（1）求出相应的变分问题的数值解uh；

（2）计算的每个网格单元上的后验误差估计(μl(T)2+μl(E)2)或ηh(T)；

（3）将误差大的单元τ标记组成集合M，使得

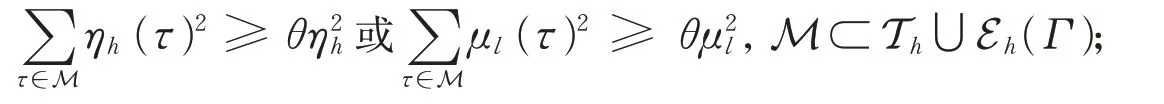
（4）细化被标记的元素得到新的网格剖分；

重复这个过程：求解→估计→标记→细化，直到数值解的误差或者细化网格的直径足够小。

4.1 数值解法

4.2 误差范数的计算

设u和uh是方程（13）和（14）的解，我们记LHS（Th1）和LHS（Th2）分别为定理1 和定理2 的误差项，GUB（Th1）和GUB（Th2）分别记为定理1 和定理2 中的后验误差估计，

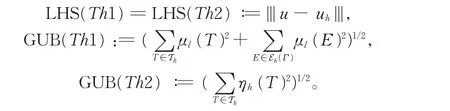
在计算误差LHS（Th1）和LHS（Th2）时，由于范数‖·‖H1/2(Ω)难以计算，将||u|Γ－uh|Γ||H1/2(Γ)利用其等价的范数‖hΓ(u|Γ－uh|Γ)′‖L2(Γ)近似，而‖u－uh‖H1(Ω)和GUB（Th1）和GUB（Th2）可利用数值求积公式计算。

4.3 实验结果

我们取Ω为单位圆，精确解u和uc的取为（41）式，其满足界面传输方程（1）。初始网格剖分取为Ω的内接正六边形，将其平均等分为六个正三角元素，在边界Γ上用直线近似，自适应细化参数取为θ=0.5。

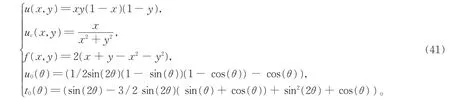
图1（a）给出了基于h－h/2 后验误差估计的自适应加密网格的三角剖分图，从图上可以看出自适应网格加密主要集中在真实解u波动较大的第三象限的区域。图1（b）给出了随着网格一致加密或自适应加密真实误差和后验误差估计量的收敛结果，从图上可以看出一致加密和自适应的结果都是收敛的，且自适应的收敛速度比一致细化得更快，说明我们的算法是有效的。

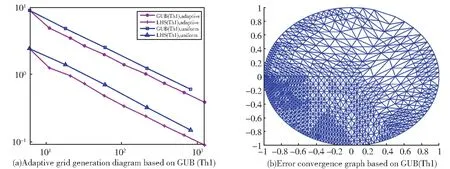
图1 基于h－h/2 后验误差估计的自适应结果（a）基于GUB（Th1）的自适应网格剖分图；（b）基于GUB（Th1）的自适应误差收敛图Fig. 1 Adaptive results of the h－h/2 posteriori error estimation（a）Adaptive grid generation diagram based on GUB（Th1）；（b）Error convergence graph based on GUB（Th1）

从图2（a）自适应剖分的结果可以看出，自适应网格加密主要集中在真实解波动较大的第三象限的区域和部分边界，这也符合我们的预期结果。图2（b）是一致剖分和自适应算法的误差收敛结果，从图上可以看出随着网格的细化，数值解和真实解的误差线性的收敛到零，且自适应误差下降速率比一致细化的快。

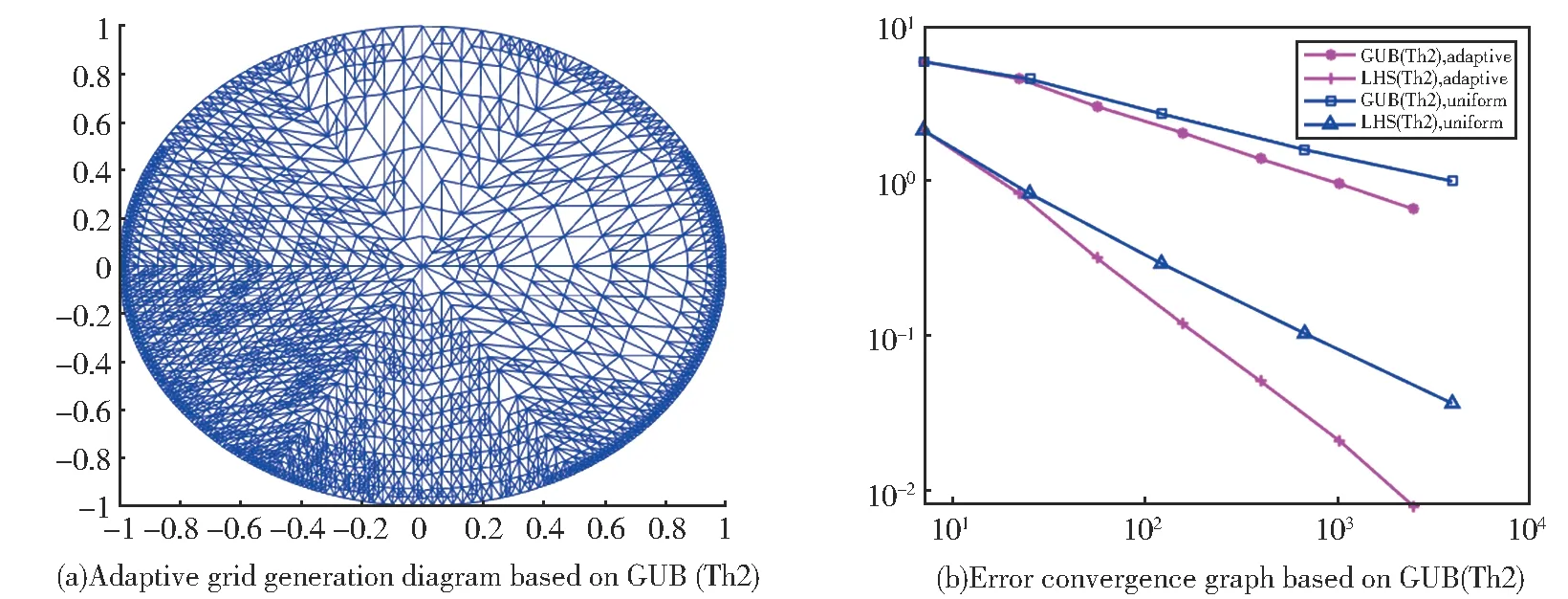
图2 基于残差的后验误差估计的自适应结果（a）基于GUB（Th2）的自适应网格剖分图；（b）基于GUB（Th2）的自适应误差收敛图Fig. 2 Adaptive results of a posteriori error estimation based on residuals（a）Adaptive grid generation diagram based on GUB（Th2）；（b）Error convergence graph based on GUB（Th2）

从上述两个后验误差的数值实验结果来看，h－h/2 后验误差估计的计算比较简单，而基于残差的后验误差估计使误差收敛地更快。