初中数学理解性教学实验研究
2018-01-02吴娟
吴娟
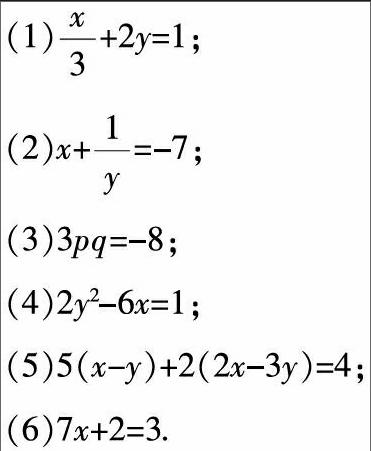
[摘 要] 教师在引导学生学习知识时,不能仅仅只是引导学生机械地记忆知识,还应引导学生深入地理解知识. 本文说明教师开展理解性教学实施的方法,只要教师应用这样的方法开展教学活动,就能让学生从抽象的角度看待知识、理解数学问题产生的机理、能根据数学问题的规律推测问题可能产生的变化,从而能灵活应用知识.
[关键词] 数学教学;理解性教学;二元一次方程
教师应用理解性教学来引导学生理解知识,是指教师通过教学活动使学生能从抽象的角度看待知识、理解数学问题产生的机理、能根据数学问题的规律推测问题可能产生的变化. 学生只有深入理解了知识,才能灵活地应用知识,深入理解知识是应用知识的基础.
引导学生在迁移中理解知识
学生理解知识时遇到的困难之一,就是觉得知识太陌生,他们不能迅速理解. 当学生在学习时感受到学习障碍,并且认为可能不能克服学习障碍时,就容易丧失学习知识的兴趣,不愿意再探索及理解知识.
教师在开展数学教学时,要帮助学生克服学习障碍,帮助学生找到学习知识的信息. 学生在课堂上、生活中已经有了一些知识经验,教师如果引导学生把新知识与旧知识结合起来,让学生以旧知识为基础,理解新知识的机理,就能让学生迅速理解新知识.
现以教师引导学生理解二元一次方程式为例. 一位教师在引导学生学习二元一次方程式以前,先引导学生思考一个问题:
小红去水果店买西瓜,她共花了18.2元买了10斤西瓜,你知道西瓜的单价是多少吗?请应用方程的形式解这一个数学问题.
对学生来说,这是一道不难的一元一次方程问题. 学生们列出方程式:设一斤西瓜为x元,西瓜单价和总价的关系为10x=18.2,解之得x=1.82,即西瓜的单价为1.82元.
当学生完成这道习题后,教师引导学生思考:在这个方程式中,“元”是什么?“次”是什么?学生回答该一元一次方程式的“元”是x,“次”为x的幂,即为1,于是它为一元一次方程式.
教师继续引导学生思考:后来小红又去水果店买东西,她这次买了5斤橙和3斤葡萄,总共花了25.4元,请问如何应用方程式来表达单价和总价的关系?
学生结合学过的知识来理解二元一次方程式的问题,学生发现,如果要用方程式来表示单价和总价的关系,那么就要涉及到橙、葡萄两件事物,如果仅用一个未知元来表达,就不能列出方程式. 学生结合新的知识与旧的知识,理解了一元一次方程式就是方程式中有1个未知元,未知元的幂为1,那么二元一次方程式,就是方程式中有2个未知元,未知元的幂为1. 它们的共同特征之一,就是它们都是方程式,具有方程式的特征;共同特征之二,就是它们的幂都只有一次. 它们的不同特征是方程中包含的“元”的个数不同,且一元一次方程式可直接求解,二元一次方程式不能直接求解,学生必须掌握其他的已知条件,才能求出二元一次方程式的解.
学生学习过一些旧知识,对旧知识的机理有一定程度的理解. 部分新知识与旧知识之间有联系,它们的知识框架有相同之处. 如果教师能够引导学生结合旧知识的框架来理解新知识的框架,学生就能从知识框架的角度理解新知识的机理. 教师应用迁移的教学方法引导学生理解知识,实际上是应用纵向对比知识的方法,帮助学生建立知识概念,当学生应用迁移的方式理解了新知识与旧知识的差异时,就能初步建立新知识的框架.
引导学生在探索中理解知识
当学生理解了概念的框架以后,需要继续深入地理解知识. 学生只有理解了概念每一句指代的性质意义,才能真正理解概念的意思,在应用概念的时候才不会犯下错误. 教师在教学中可以为学生布置典型的习题,引导学生从横向、纵向对比来理解概念. 教师引导学生横向、纵向对比的过程,就是引导学生探索知识的过程,学生在对比中,可以全方位地了解新知识的特点,这一特点就是新知识概念区分于旧知识概念的地方.
以教师引导学生学习二元一次方程,深入理解二元一次方程的特点为例,教师可引导学生思考以下习题:请分析以下的算式哪些是二元一次方程:
学生经过思考,首先排除掉(4)和(6),教师引导学生思考为什么这两个不是呢?学生表示(4)中虽然出现了x,y两个未知元,但y的次数是2,它属于二元二次方程式. (6)是一元一次方程式. 关于(3)是不是二元一次方程式,很多学生犯了难,教师引导学生再次阅读数学概念,并引导学生思考整式的次数是如何决定的. 学生经过思考,发现(3)的阶次是两次,它不是一次方程式,这就如同ax·x或ax·y的阶次都不是一次一般. 学生排除了(3)后,有学生指出,如果排除掉(3),那么(2)也必须排除,因为如果将(2)去分母,整合成方程标准式后,它为xy+1=-7y,即xy+7y+1=0,它的阶次也为2. 教师引导学生结合这一题开始思考,二元一次方程式是什么?请用多种方法描述出来. 学生结合这一道题与教师的提示,开始思考二元一次方程式的标准表达式、性质、表格的表示方法、坐标图像的表示方法等.
当学生理解了新知识的框架以后,可能对概念还不太熟悉,应用概念知识时可能存在一些问题. 教师可以为学生布置数道习题,引导学生一一探讨数学概念每一句描述的意思,让学生从横向对比的角度理解知识概念. 这样能让学生对比微观案例来理解宏观概念的意思,了解每一句宏观概念描述的意义,并理解概念描述的每一句话之间的内在关系. 这一教学过程是教师帮助学生填补新框架知识内容不足的过程.
引导学生在生活中理解知识
当学生从横向与纵向两个角度理解了知识框架,找寻出知识框架的雏型以后,教师可为学生布置典型的习题,让学生在应用中进一步理解知识.
现以教师引导学生思考以下习题为例:
甲车、乙车在周长为400米的环形跑道上移动,如果同时、同地、反向出发,两车经过80秒相遇. 已知乙车的速度是甲车速度的,求甲车、乙车的速度.
在这一次的学习中,学生发现了:
第一,在解决一个数学问题时,如果存在两个未知量,那么可用设x和y元的方法列方程,应用这种方法可让数学问题变得更简单.
第二,应用二元一次方程方法的要求,就是科学地设元及根据已知條件列出等量关系.
第三,在考虑问题时,可以应用多种方法来解决问题,从中找到最佳的解决方案,学生学习的知识越多,就意味着学生可以采取的数学方案越多.
当学生获得了知识框架以后,教师要引导学生在实践中思考问题:
第一,教师要引导学生在实践过程中思考知识概念的应用方法,从应用的角度更深入地理解知识;
第二,引导学生对比用旧知识解决问题和用新知识解决问题存在的差异,让学生再次从对比中理解新知识与旧知识的关联和差异,使学生能整合出较为完善的数学知识体系.
教师理解性教学分为三个步骤:
第一,引导学生迁移,从旧知识框架的角度理解新知识的框架;
第二,引导学生横向对比,让学生深入理解新框架中每一条概念的意思;
第三,引导学生应用新知识框架,让学生从实践的角度再次横向及纵向对比,整合出较为完善的知识结构.endprint
