二次方程的实根分布问题分类解析

鲍人灯

(浙江省天台育青中学 317200)

二次方程的实根分布问题分类解析

鲍人灯

(浙江省天台育青中学 317200)

本文就高考复习中的一类常见题型——含参的二次方程实根分布问题的求解方法，分类归纳，并举例说明，对高考备考专题复习有参考价值.

二次方程；实根分布；区间；取值范围

由二次方程的实根分布来求参数的取值范围问题是对初中有关二次方程、二次函数的进一步深化，并构成高中数学的基本知识块，是各种数学思想的交汇处，更是高考考查的热点.本文从函数、方程、不等式诸角度对这类问题分类解析，以使考生明确思路，掌握方法，从容解答.

一、二次方程实根分布的类型

为了简化情况，方便行文，我们约定二次方程f(x)=ax2+bx+c=0(a>0)的两个实根分别为x1、x2.下面将实根范围的约束条件分类整理如下.

1.方程的两个实根均小于常数m

2.方程的两个实根均大于常数m

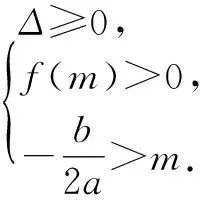
3.方程的一个实根大于常数m，另一个实根小于常数m.

方法①f(m)<0.

方法②(x1-m)(x2-m)<0.

说明：①是从二次函数图象的位置来思考的；

②是从根与m差的符号来考虑的.

4.方程在区间(m,n)内恰有一个实根

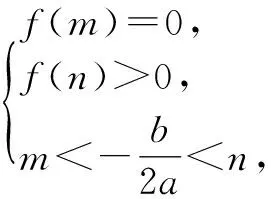
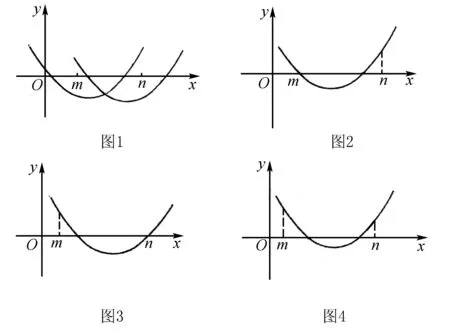
5.方程在区间(m,n)内恰有两个实根

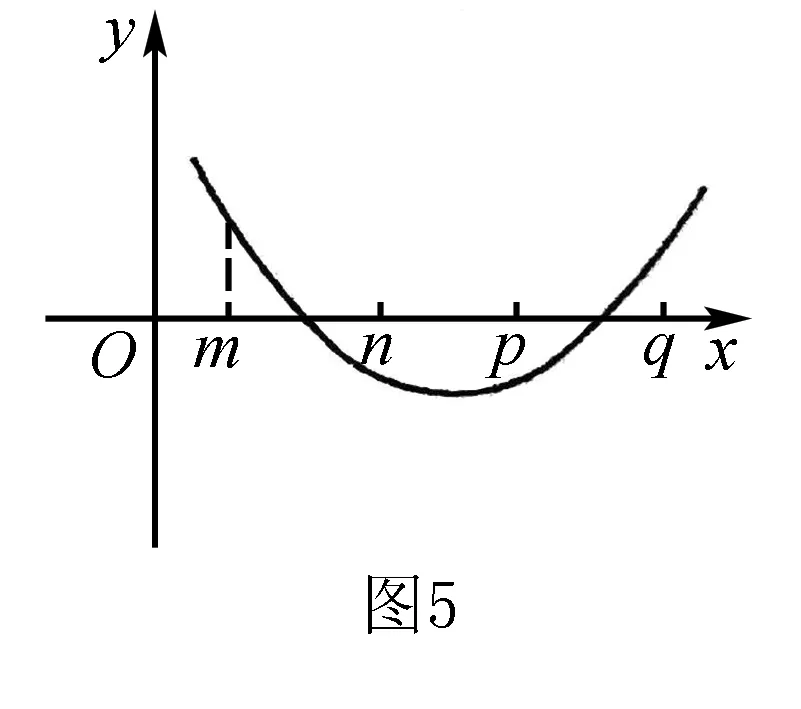
6.方程的两个实根分别在区间(m,n)和(p,q)(n≤p)内.

二、应用举例

例1 若方程-x2+2ax+a-2=0有两负根，求a的取值范围.

解先化成f(x)=x2-2ax-a+2=0.

方法1 结合二次函数f(x)的图象，知有

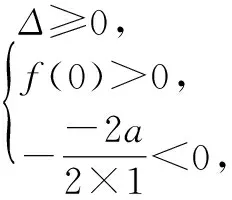
解得a≤-2.

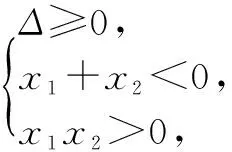
解得a≤-2.

例2 二次函数f(x)=x2-4mx+2m+6在区间(-3，0)内恰有一个零点，求实数m的取值范围.

解结合相应二次函数f(x)的图象与区间(-3，0)的位置关系，有四种情况.

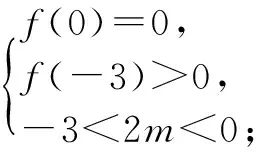
点评二次函数零点个数与二次方程实根个数既相关，又有区别.二次方程有两个相等的实根时，对应的二次函数有一个零点.这是本题容易混淆之处，而遗漏情况④.

例3 方程(2m+1)x2-2mx+(m-1)=0,(1)有两个异号根；(2)有正根.分别求实数m的取值范围.

当2m+1≠0时，方程是二次方程，相应的二次函数f(x)=(2m+1)x2-2mx+(m-1)的图象有四种符合要求的情况(如图6，图7).因此有不等式组：

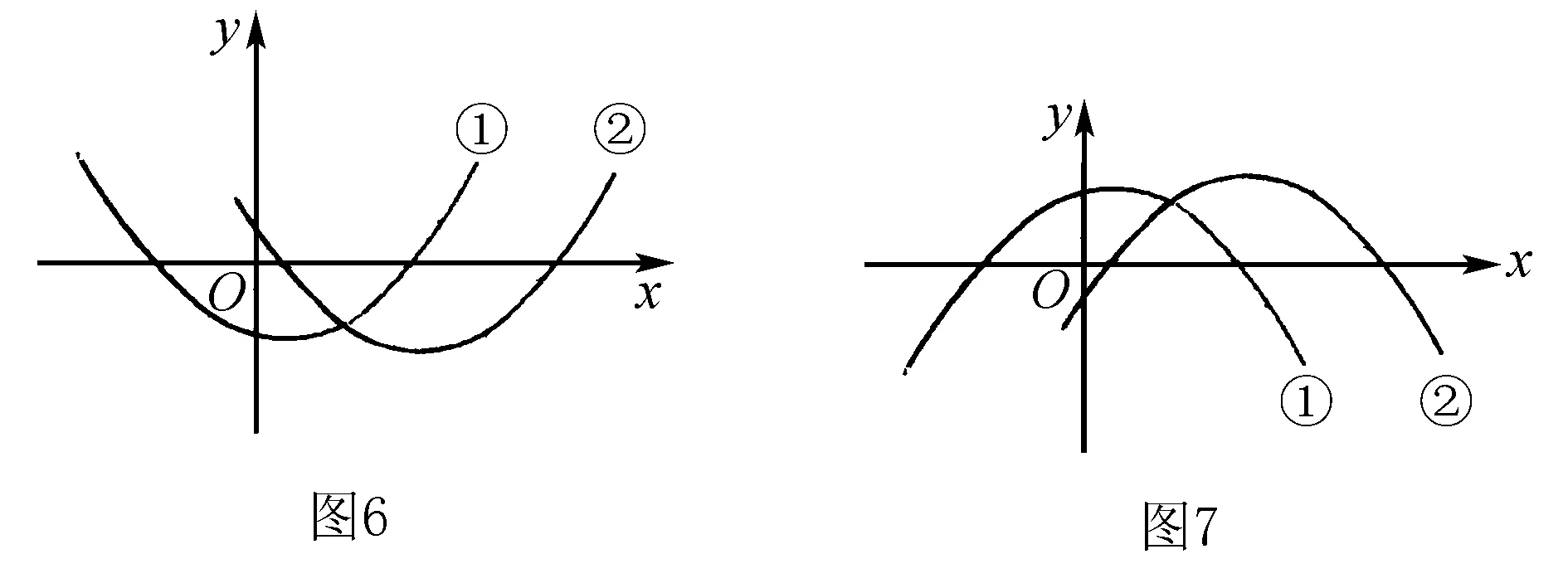
上式中的Δ=(-2m)2-4(2m+1)(m-1)=-4m2+4m+4.

分别求解四个不等式组，得

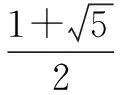
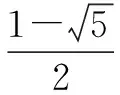
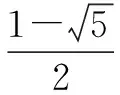
(2)小题求解时易漏掉2m+1=0的情况；而当2m+1≠0时，情况也较多，应分情况一一考虑.本小题考查了思维的全面性、慎密性.

从以上可以看出，二次方程实根分布问题，涉及到数学中的函数与方程、数形结合、分类讨论、化归转化等四大数学思想，是锤炼学生全面数学能力的重要知识板块.因此，在总复习时，很有必要进行专题复习，从中掌握思想方法，全面提升数学素养.

[1]刘鹏.参数取值范围问题的求解方法[J].高中数学教与学，2014(1)：19-21.

[2]夏丽琴.含参函数在定区间上存在零点问题的探究[J].中学数学研究，2014(2)上：29.

[3]刘鸿春.多变量中复合最值问题的探求[J].数学通讯，2014(3)上半月：12-13.

[4]石礼标，刘陆军，蒋明建.一道范围问题的简解与推广[J].数学通讯，2014(3)上半月：26-28.

[5]杨春娟.含参一元二次不等式的解法与恒成立问题[J].中学生数学，2015(2)上：28.

G632

A

1008-0333(2017)31-0026-03

2017-07-01

鲍人灯(1981.10-)，男，中学一级教师，大学本科，从事高中数学教学。

杨惠民]