轴向移动悬臂梁高效动力学建模及频率响应分析1)
2017-12-18华洪良廖振强张相炎
华洪良 廖振强 张相炎
(南京理工大学机械工程学院,南京210094)
轴向移动悬臂梁高效动力学建模及频率响应分析1)
华洪良 廖振强2)张相炎
(南京理工大学机械工程学院,南京210094)
轴向移动梁动力学问题具有广泛的工程应用背景,如:机械手、机床主轴、武器身管等.计算轴向移动梁动力学响应是评估结构动力学性能以及最终指导结构设计的一个重要手段.采用Rayleigh-Ritz法、拉格朗日方程推导了轴向移动悬臂梁时变动力学方程.选取幂级数函数构造试函数对轴向移动系统动力问题进行求解.幂级数函数良好的积分与微分性能,使得推导容易以矩阵的形式快速进行,便于符号运算软件直接生成MATLAB程序.由于MATLAB基本数据单位为矩阵,符号软件生成的程序只需经过简单修改便可进行动力学计算.大大缩短了轴向移动梁从建模到动力学分析的时间,过程十分高效.通过四组算例,将本文方法计算得到的动力学响应与文献数据进行对比,对该方法准确性进行了验证,并给出了幂级数函数拟合阶数的选取原则.以此为基础,研究了轴向移动梁的频率响应特性.分为考虑重力与忽略重力两种情况,讨论了轴向振动幅度对其频率响应特性的影响.
计算动力学,幂级数基函数,频响分析,轴向移动梁
引言
轴向移动动力系统具有广泛的工程应用背景,常见的有:机械手、机床主轴、武器身管[1-3]、传送带[4-6]、卫星结构等.近年来,轴向移动系统动力学是一研究热点.由于动力响应在评估结构动力学性能以及最终结构设计中不可或缺,因此,一种快速、准确的建模与响应分析方法在轴向移动系统动力学研究过程中至关重要.
在轴向移动系统动力学研究中,通常将轴向移动系统简化为轴向移动弦或轴向移动梁.根据已有文献,目前轴向移动系统动力学研究主要集中于如下几类问题:轴向移动弹性梁与旋转刚性支撑的耦合动力学[7-9],轴向移动黏弹性梁 (或弦)[10-14]、外流体轴向移动梁[19-22]、含有摩擦边界的轴向移动梁[23-24]、轴向移动梁的参数振动[25-26]、轴向移动梁横向振动抑制技术研究[27-28]、轴向与横向耦合振动研究[29-31]等.
在轴向移动系统动力学建模过程中,主要有两种方法.第一种为分析力学方法[7-10,29-30,32-35],并且应用最为广泛的分析力学方法为第二类拉格朗日方程.在该方法中,首先采用能量法对系统进行能量分析,得到相应的拉格朗日函数,经离散后采用拉格朗日方程推导得到其运动方程.第二种为弹性力学方法[12,14-24,26-28,31,34,37].采用该方法时,首先对研究对象取分离体进行受力分析,得到其控制方程,经离散后直接得到其运动方程.
在离散过程中,两种主要的离散技术为有限单元法[8-9,32-33,38]与假设模态法[34-37].在假设模态法中,需要一系列满足所有(或者部分)边界条件的基函数来构造一个试函数对原函数进行逼近.在轴向移动梁控制方程离散过程中,通常选取其振型函数来构造试函数.梁的振型函数由一系列三角函数与双曲函数构成,形式复杂,其复杂程度取决于其具体边界条件.在常见的边界条件中,只有简支边界梁的振型函数相对简单,而固支边界、自由边界、悬臂边界等梁的振型函数较复杂.在建模过程中,通常需要采用振型函数之间的正交性对方程进行解耦.然而,由于梁的轴向运动,在其动力学建模过程中会产生诸多不同于定常结构的陀螺项,利用目前已知的模态函数正交性条件尚无法使这些陀螺项完全解耦[39],因此轴向移动梁动力学建模尚无统一方法.
基于上述因素,本文尝试采用幂级数作为基函数构造试函数对轴向移动系统动力问题进行求解.由于幂级数基函数具有较好的积分与微分性能,更重要的是对任何两个基函数之间的正交性并不敏感.这一特点,使得积分演算变得非常迅速,并且对于不同问题均很容易以矩阵的形式进行推导,推导过程更为简洁.采用矩阵形式的最主要优势在于:能够采用符号运算软件推导并直接生成MATLAB程序.由于MATLAB基本数据单位为矩阵,符号软件生成的程序只需经过简单修改便可进行动力学计算.这样大大缩短了轴向移动梁从建模到动力学分析的时间,提高了效率.
本文主要工作:
(1)基于欧拉梁理论,首先推导了轴向移动梁动能与势能函数,考虑时变轴向移动速度.随后,采用Rayleigh-Ritz法与幂级数基函数对系统动能与势能函数进行离散,并通过拉格朗日方程推导得到系统运动方程.
(2)将本文计算得到的动力学响应与相关文献数据进行比较,对本文方法与模型的准确性进行验证.并给出幂级数函数拟合阶数的选取原则.
(3)研究轴向往复运动频率对横向振动的影响,即频率响应分析(身管武器应用背景).分为考虑重力与忽略重力两种情况进行讨论.
1 动力学建模
考虑一轴向移动悬臂梁模型,如图1.梁总长LB,悬臂长L(t).杨氏模量、惯性矩、密度、截面积分别为E,I,ρ,A.梁横向位移采用w(x(t),t)进行描述.
梁上任意一点发生变形后,其位移矢量为

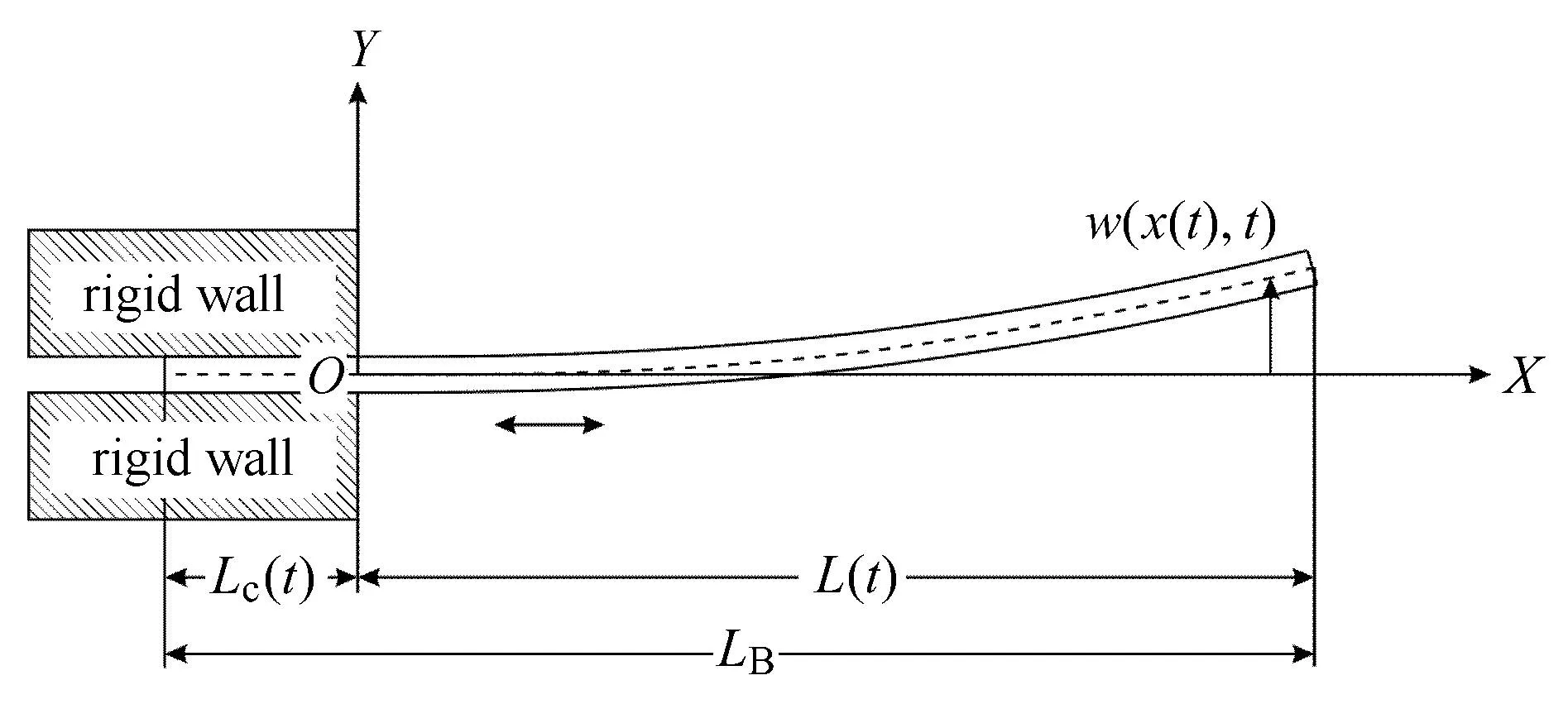
图1 轴向移动悬臂梁Fig.1 Axially moving cantilever beam
将式(1)对时间求导得到速度矢量
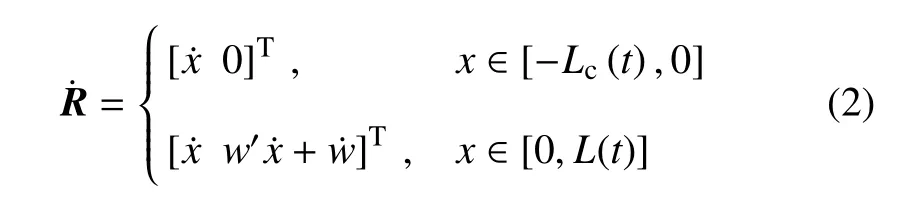
式中,点和撇分别表示对时间、空间求偏导.根据式(2),系统动能为
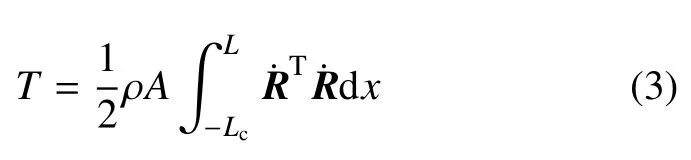
梁弯曲变形产生的应变能为
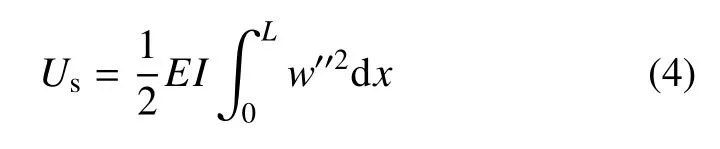
考虑梁轴向运动存在加速度,其轴向惯性力产生的拉伸应变能为
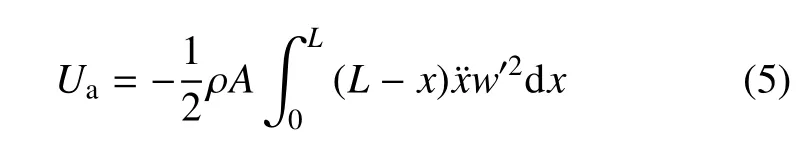
根据式(3)∼式(5),得到系统拉格朗日函数
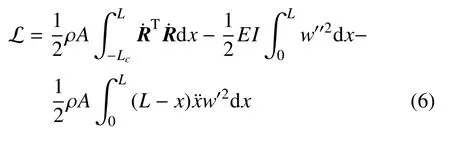
2 离散与运动方程
首先构造试函数

对梁的横向位移进行离散.式中

在式(8)中
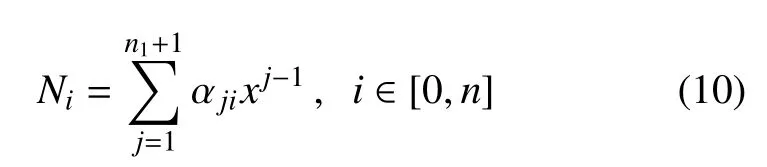
为满足悬臂梁边界条件的幂级数函数.式中,n1为幂级数函数阶数;αji为幂级数函数系数,确定αji的一个简易方法就是对悬臂梁振型函数进行拟合.在拟合前,首先将悬臂梁振型函数
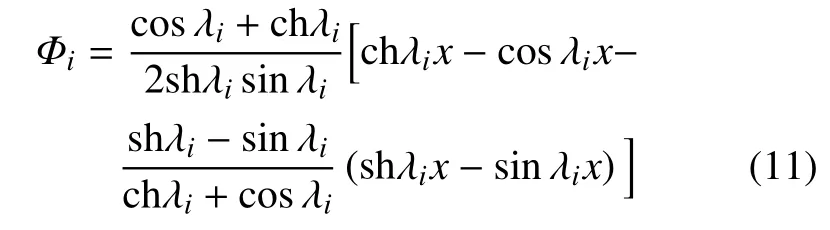
映射至 1-1空间.式中,cosλi+chλi/2shλisinλi为一系列幅值映射系数;λi为特征方程cosλichλi+1=0的根.经过该映射后,梁长度与自由端横向位移均被无量纲化为1.将梁长度映射为1后,有利于后续缩放为梁实际悬臂长度进行动力学计算.将梁自由端横向位移映射为1后,结果后处理将变得十分简单,梁自由端真实的横向位移即为各基函数坐标的和.
式(10)中幂级数系数可根据式(11)拟合得到.对于自适应任意悬臂长度的基函数可以将式(10)沿X轴缩放得到

将式(7)代入式(6),并将结果代入拉格朗日方程,把重力作为广义力考虑,得到系统运动方程
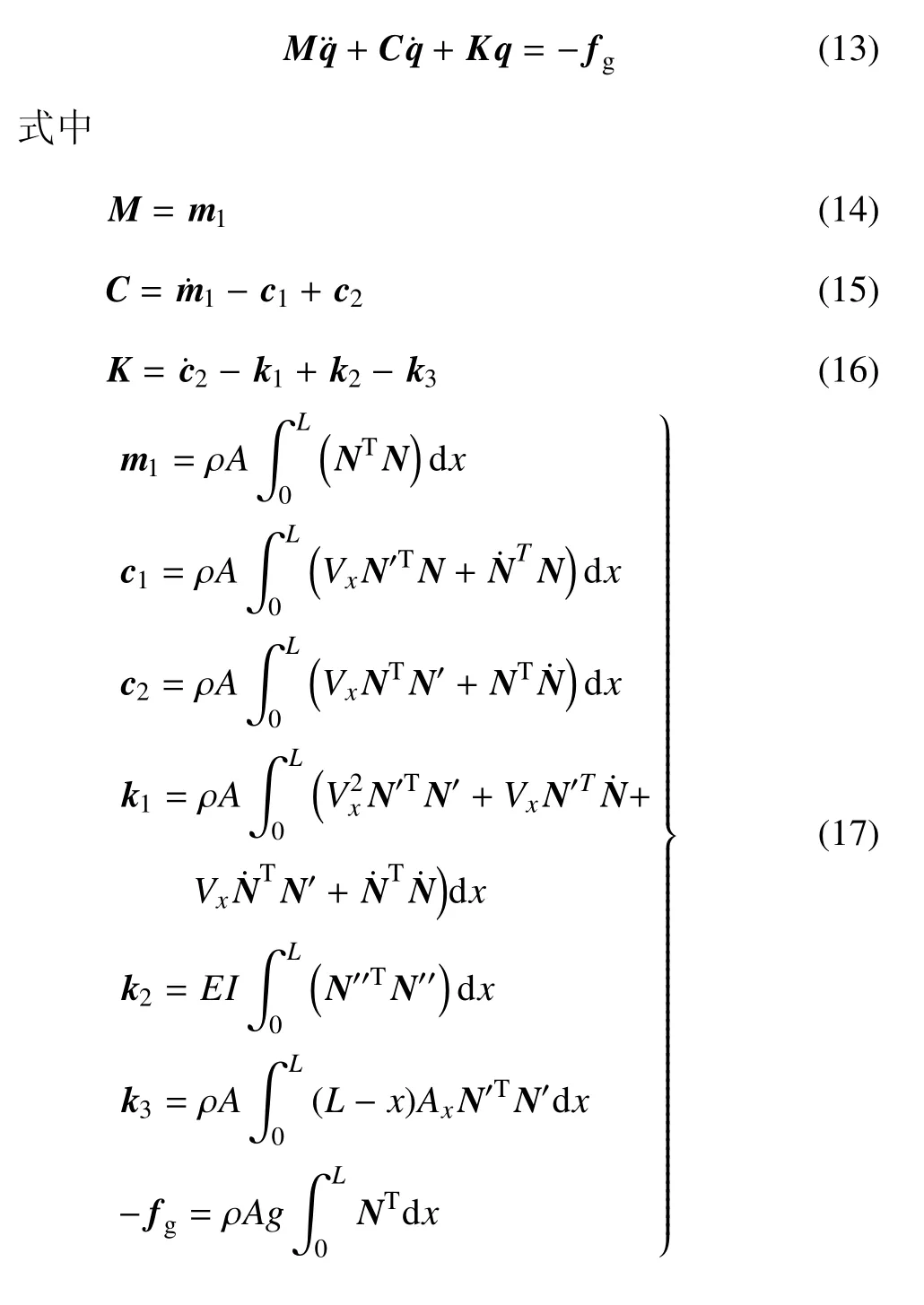
值得一提的是,式(13)中C为梁弯曲变形与轴向运动产生的陀螺项,而非结构阻尼.并且,Vx=与Ax=分别为梁轴向运动速度与加速度.Vx=V0+Axt,V0为初始速度.由于式(17)为一系列幂级数函数乘积的积分运算,很容易采用符号运算软件进行推导得到其代数格式,并自动生成MATLAB程序.
3 模型验证
本节采用4个算例对本文方法准确性进行验证.前两个算例源于文献[36],在该算例中,梁作轴向匀速运动.后两个算例源于文献[29],算例中梁作轴向匀加速运动.4个算例中,梁截面积、杨氏模型、惯性矩、密度均一致,分别为1.4661×10−3m2,6.8335N/m2,1.1073×10−8m4,2738.6kg/m3.其余参数设置见表1.
计算得到的梁自由端动力学响应与文献[36]和文献[29]对比见图2和图3.本文计算结果与文献结果吻合较好,说明本文采取的方法以及建立的模型准确可靠.
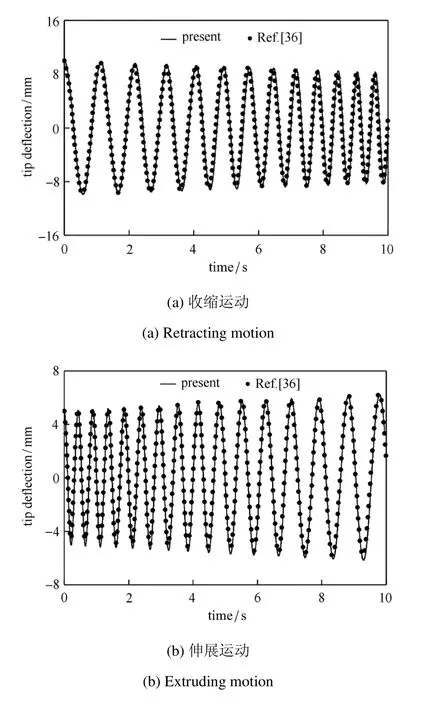
图2 匀速收缩、伸展运动Fig.2 The retracting and extruding motion with constant velocity

图3 匀加速收缩、伸展运动Fig.3 The retracting and extruding motion with constant acceleration

表1 验证算例物理参数Table 1 Physical parameters of the veri fi cation examples
4 幂级数基函数拟合阶数的影响
第2节中,幂级数函数拟合阶数n1的大小将直接决定幂级数基函数的拟合精度,并最终影响到动力学计算精度.本节主要讨论幂级数拟合阶数对动力学计算精度的影响.
根据式(11),采用MATLAB软件编程,在计算域内对各振型函数均匀采样,本文采用500个样本点.然后根据得到的样本点以及给定的拟合阶数,采用poly fi t函数便可拟合得到幂级数函数系数αji.为了给出拟合阶数的选取原则,采用幂级数函数的最大相对拟合误差作为量化指标
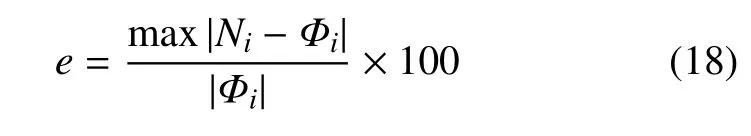
需要说明的是,笔者在研究过程中发现在多数情况下,细长悬臂梁结构动力响应主要取决于其一阶模态.因此,本节只讨论第一阶模态拟合阶数对动力学计算精度的影响.通过计算,在表2中给出了拟合阶数为1至10范围内的最大相对拟合误差.对比发现,随着拟合阶数的增大,幂级数函数的最大相对拟合误差逐渐减小.
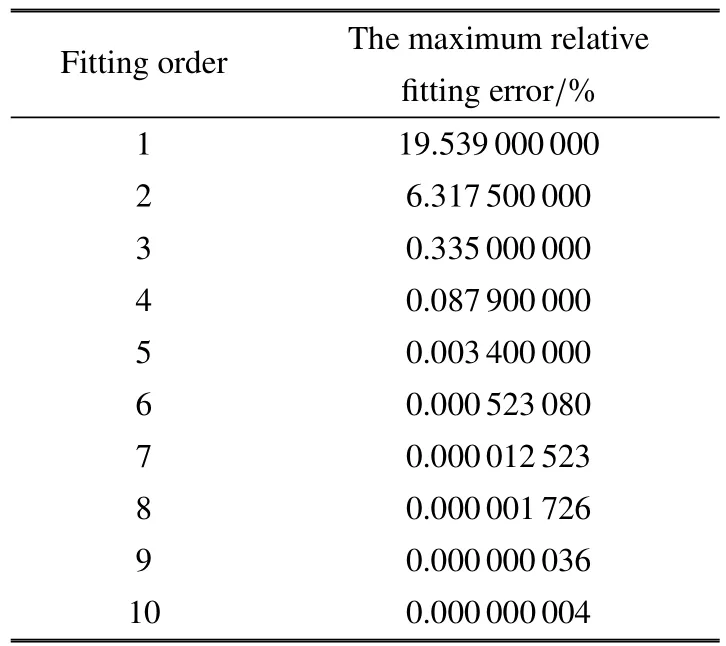
表2 最大相对拟合误差Table 2 The maximum relative fi tting error
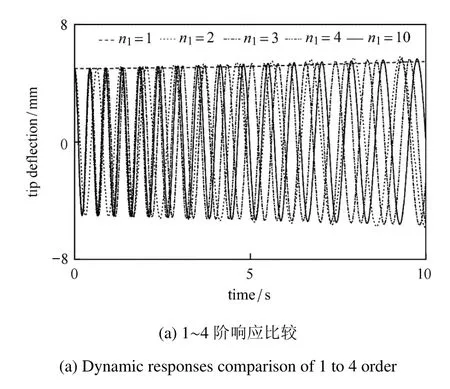
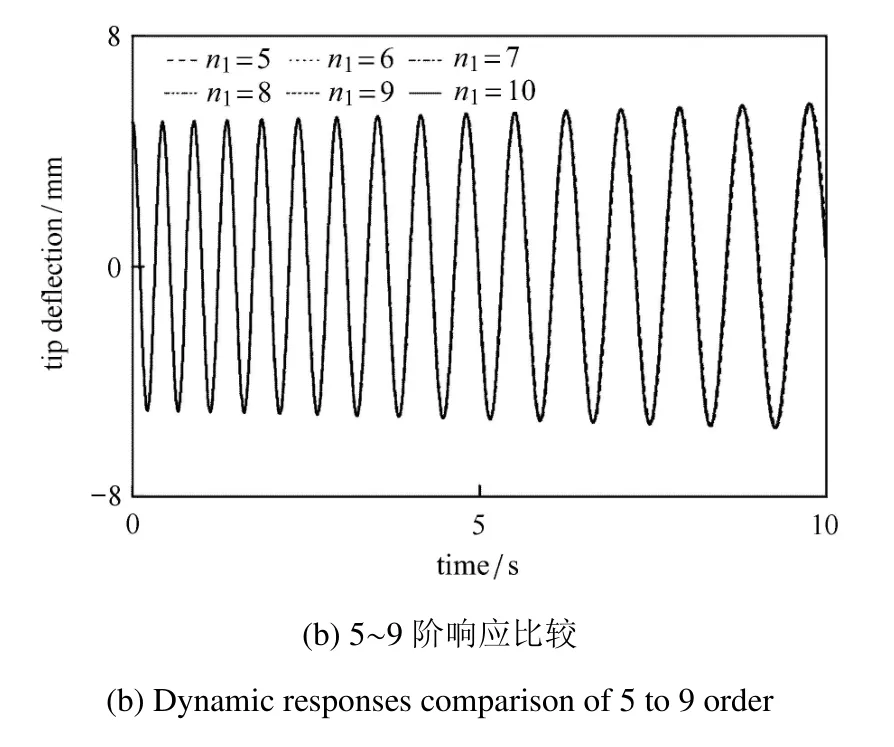
图4 幂级数函数拟合阶数对动力学计算精度的影响Fig.4 The e ff ect of fi tting order of the power series function on computational accuracy
随后,以第3节算例2为例,分别采用不同拟合阶数的幂级数函数进行动力学计算,得到梁自由端位移响应曲线对比如图4.以10阶拟合精度的幂级数函数计算得到的动力学响应曲线为参考进行对比研究.图4(a)表明,当拟合阶数在1至4阶范围内时,动力学计算产生了较大的误差.尤其是当拟合阶数为1时,计算得到的响应曲线根本无法反应梁的真实振动情况.这是因为采用一阶幂级数函数时,式(17)中N00对空间X求导两次后为零,相当于结构刚度消失.当拟合阶数增加至5阶及其以上后,响应曲线与10阶响应曲线基本吻合,差异很小.因此,为了保证动力学计算精度,应采用至少5阶幂级数函数进行拟合.由表2可知,5阶幂级数函数对应的最大相对拟合误差为0.0034%.因此,笔者建议在选取幂级数函数拟合阶数时,应将其最大相对拟合误差控制在千分之一以内.
5 频响分析
本节讨论轴向振动频率对梁横向振动的影响.其工程应用背景为武器浮动身管.很多身管武器在设计过程中,为了减小后坐力,经常将其身管设计为浮动形式,使得身管在发射过程中能够沿着枪(炮)身做前后相对运动,吸收一部分后坐动能.武器连续发射过程中,身管不停地做轴向往复运动,使得膛口横向振动受到扰动.由于身管的射击精度直接于弹头出膛口瞬时膛口的振动状态.因此,研究此类振动系统的频响特性对匹配身管武器系统动力学特性、避免结构共振具有重要意义.
在研究频响特性时,使轴向移动梁做轴向简谐运动,其悬臂长度、轴向速度、加速度由下式给出

式中,L0表示梁平均悬臂长度;Amp和ω分别表示简谐运动幅值与频率.算例所用参数设置如表3.
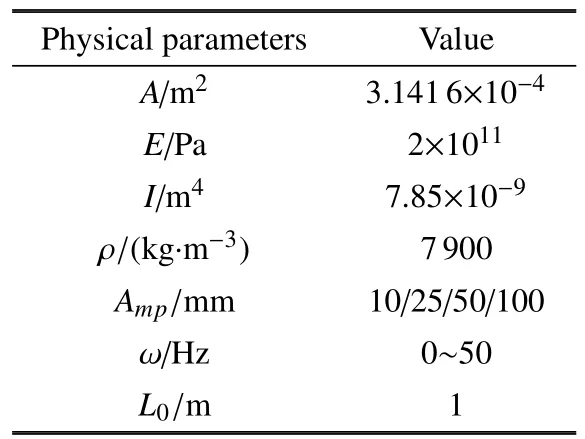
表3 算例参数Table 3 Example parameters
5.1 考虑重力影响
图5给出了不同轴向振动幅值下的梁自由端频率响应特性曲线.从图5可以发现,轴向振动幅值越大,幅频响应曲线中特殊频率点越多.当轴向运动幅值为10mm时(图5(a)),幅频响应曲线中只有c和d两个特殊频率点.当轴向运动幅值增加至100mm时,幅频响应曲线中共出现了5个特殊频率响应点,如图5(d),各频率值见表4.
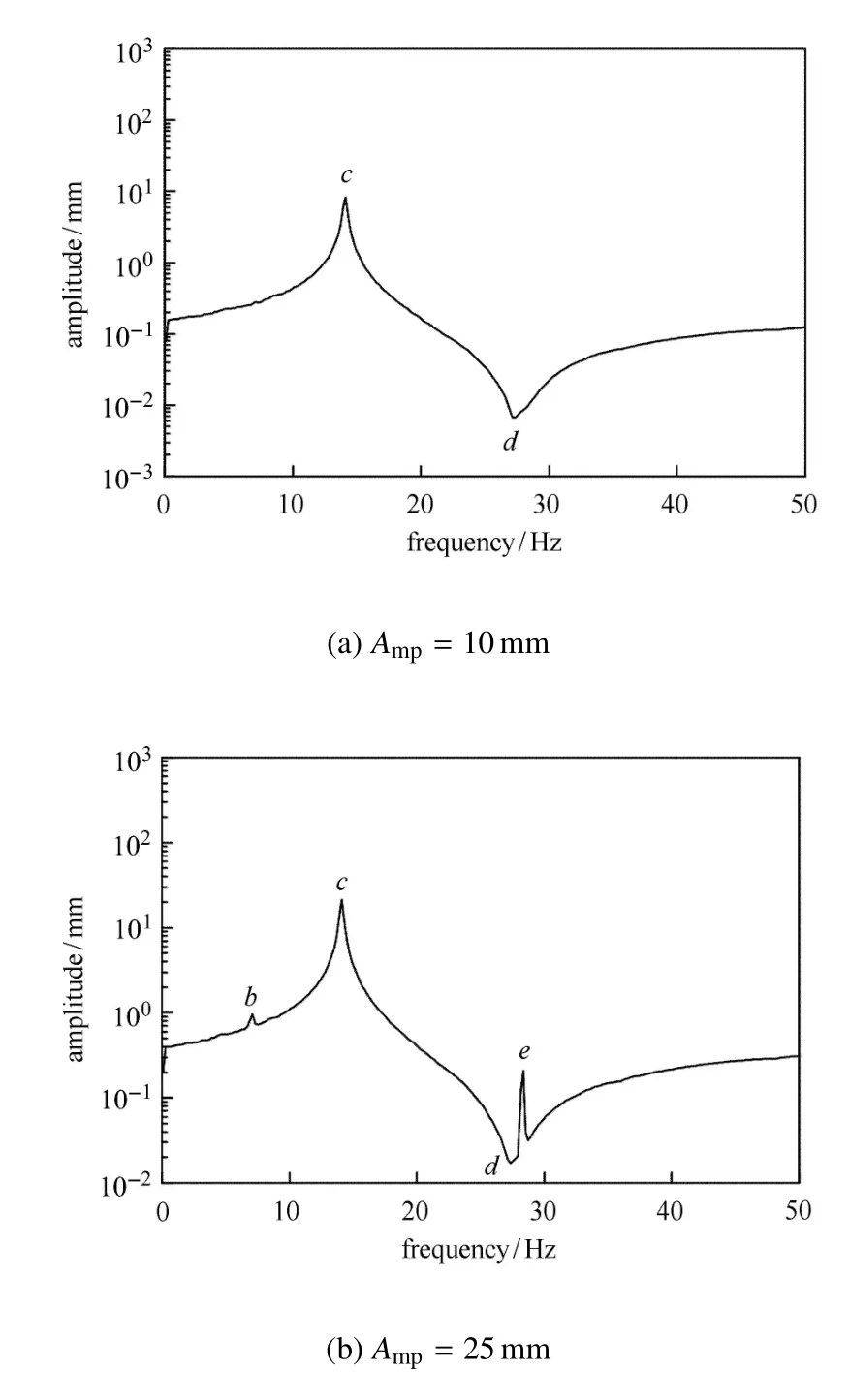
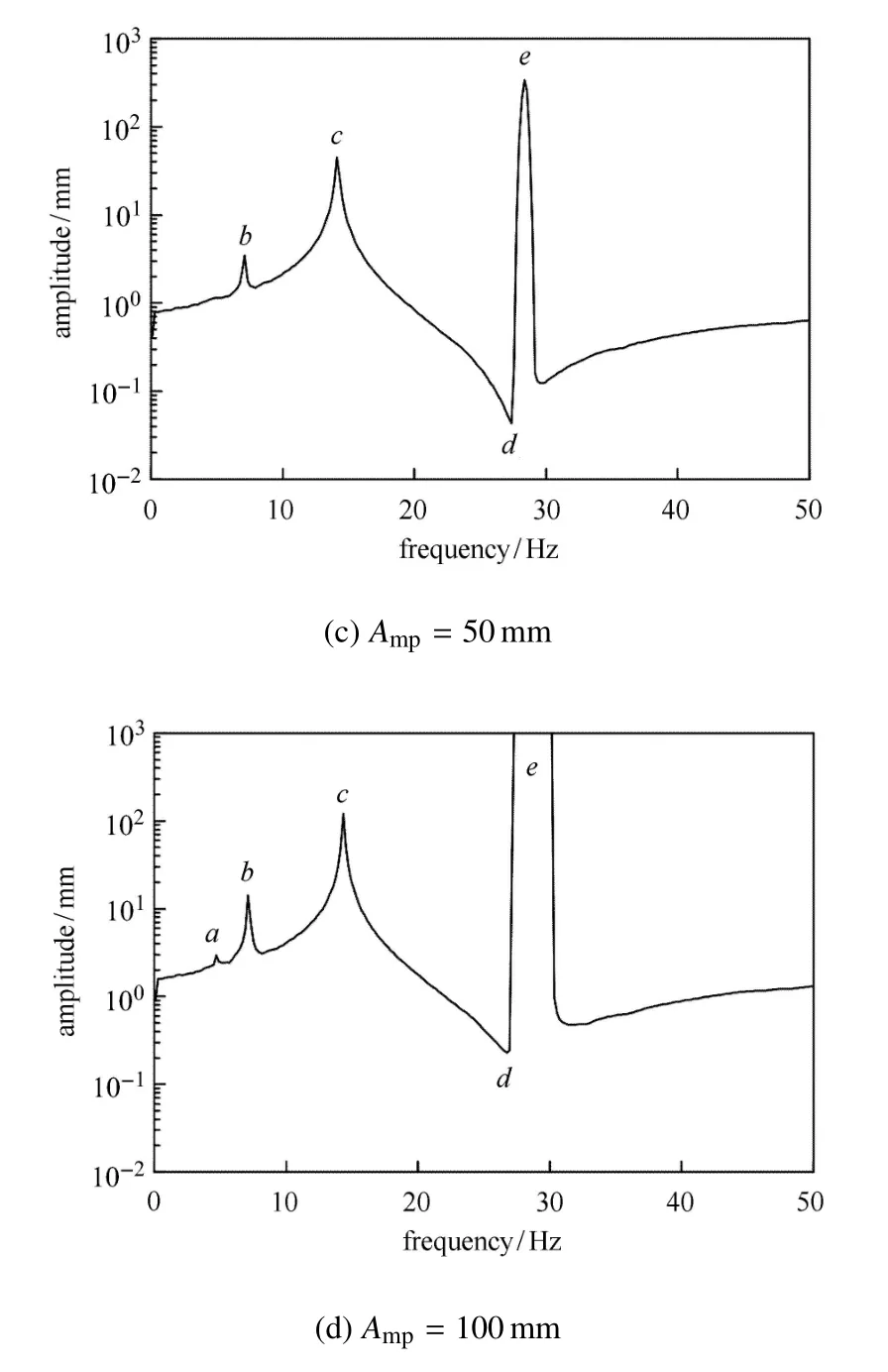
图5 轴向移动梁频率响应特性(考虑重力)Fig.5 Frequency response characteristic of the axially moving beam(considering gravity)

表4 各频率响应点频率值(Hz)Table 4 Frequency of each response point(Hz)
当梁轴向振动频率由频率点c向频率点d靠近过程中,梁横向振动幅度逐渐减小,并在频率点d达到最小值.因此,在往复轴向运动系统动力学设计过程中,匹配其轴向振动频率使其尽可能接近d频率点,能够有效减小横向振动,改善系统动力性能.
然而,需要注意的是d频率点会因梁轴向振动幅度而变得不稳定,见图5(b)∼图5(d).随着梁轴向振动幅度的增加,在频率曲线中d频率点附近会出现e频率点,该频率点为不稳定频率点.当梁在e频率点做轴向振动时,梁横向振动幅度迅速增加并失稳,如图5(d).并且,e频率点频带宽度会随着梁横向振动幅度的增大而增大,对梁的横向振动十分不利.避免e频率点出现的一个有效方法就是调整梁轴向振动幅度.
笔者发现,在重力作用下,各频率点频率值分布有一定规律性:梁平均悬臂长度对应的第一阶模态频率为14.07Hz,a,b,e频率点频率值分别分布在梁第一阶模态频率的1/3,1/2,2倍处附近.因此,在轴向运动系统动力学设计过程中,不仅要使轴向振动频率避开一阶模态频率.在轴向振动幅值较大的情况下,避开一阶模态频率的1/3,1/2,2倍频率值也是必要的.
5.2 忽略重力影响
将重力加速度g设为0,则可忽略重力对梁横向振动的影响.同样分析不同轴向振动幅值下的梁频率响应特性,结果见图6.
对比图5与图6可以发现,忽略重力影响后,梁的频率响应特性变得相对简单.当梁轴向振动幅度较小时,轴向运动频率对梁的横向振动影响很小,如图6(a).随着梁轴向振动幅度的增大,频响曲线在28.36Hz附近出现共振峰(即5.1节中e频率点),使系统失稳.梁轴向振动幅度越大,e频率点共振带宽越大,这一现象与文献[33]得出的结论一致.
关于轴向运动梁的稳定性,主要是由于式(15)中的C为一陀螺项,其符号受到梁运动方向的影响,即:梁做伸展运动时,C符号为正,具有阻尼效应,能够耗散系统能量使系统获得稳定.当梁做收缩运动时,C符号为负,收缩运动过程中梁会从固定边界处吸收能量,使系统处于不稳定运动状态,甚至失稳.关于轴向运动梁的稳定性的详细讨论,可参考文献[32].


图6 轴向移动梁频率响应特性(忽略重力)Fig.6 Frequency response characteristic of the axially moving Beam(neglecting gravity)
6 结论
本文采用Rayleigh-Ritz法、拉格朗日方程推导了轴向移动悬臂梁时变动力学方程.与以往离散方法不同的是,本文选取幂级数函数构造试函数对轴向移动系统动力问题进行求解.由于幂级数基函数具有较好的积分与微分性能,这一特点使积分运算变得非常迅速,并且很容易以矩阵的形式进行推导,并可以采用符号运算软件直接生成MATLAB程序.由于MATLAB基本数据单位为矩阵,符号软件生成的程序只需经过简单修改便可进行动力学计算.这样大大缩短了轴向移动梁从建模到动力学分析的时间,过程十分高效.相关算例对比表明,本文采取的方法与建立的模型准确可靠.
通过建立的时变动力学方程对梁的轴向共振问题进行了研究,得到如下结论:
(1)在选取幂级数函数拟合阶数时,应将其最大相对拟合误差控制在千分之一以内,以保证较好的动力学计算精度.
(2)轴向振动幅值越大,幅频响应曲线中特殊频率点越多,并且容易导致系统失稳.同时,失稳频率宽度越大.
(3)考虑重力影响时,会在梁一阶模态频率值的1/3、1/2、2倍处附近产生共振峰.共振峰峰值随着轴向振动幅度的增加而增加.忽略重力影响,即梁在水平面内的振动,梁的频率响应特性相对简单,只在梁一阶模态频率值的2倍处附近出现系统失稳.
1 Gimm HI,Cha KU,Cho CK.Characterizations of gun barrel vibrations of during fi ring based on shock response analysis and shorttime Fourier transform.Journal of Mechanical Science and Technology,2012,26(5):1463-1470
2 Hua HL,Liao ZQ,Song JE.Vibration reduction and fi ring accuracy improvement by natural frequency optimization of a machine gun system.Journal of Mechanical Science and Technology,2015,29(9):3635-3643
3 刘宁,杨国来.移动质量作用下轴向运动悬臂梁振动特性分析.振动与冲击,2012,31(3):102-105(Liu Ning,Yang Guolai.Vibration property analysis of an axially moving cantilever beam with the effect of a moving mass.Journal of Vibration and Shock,2012,31(3):102-105(in Chinese))
4 SuwekenG,VanHorssenWT.Onthetransversalvibrationsofaconveyor belt with a low and time-varying velocity.Part II:The beamlike case.Journal of Sound and Vibration,2003,267(5):1007-1027
5 Pakdemirli M,Oz HR.In fi nite mode analysis and truncation to resonant modes of axially accelerated beam vibrations.Journal of Sound and Vibration,2008,311(3-5):1052-1074
6 Ponomareva SV,van Horssen WT.On the transversal vibrations of an axially moving continuum with a time-varying velocity:Transient from string to beam behavior.Journal of Sound and Vibration,2009,325(4):959-973
7 Al-Bedoor BO,Khulief YA.Vibrational motion of an elastic beam with prismatic and revolute joints.Journal of Sound and Vibration,1996,190(2):195-206
8 Al-Bedoor BO,Khulief YA.Finite element dynamic modeling of a translating and rotating fl exible link.Computer Methods in Applied Mechanics&Engineering,1996,131(1):173-189
9 Al-Bedoor BO,Khulief YA.General planar dynamics of a sliding flexible link.Journal of Sound&Vibration,1997,206(5):641-661
10 Lee U,Oh H.Dynamics of an axially moving viscoelastic beam subject to axial tension.International Journal of Solids and Structures,2005,42(8):2381-2398
11 丁虎,陈立群.轴向运动黏弹性梁平面耦合非线性受迫振动.上海大学学报(自然科学版),2009,15(6):649-652,658(Ding Hu,Chen Liqun.Coupled forced response of nonlinear axially moving viscoelastic beam.Journal of Shanghai University(Natural Science Edition),2009,15(6):649-652,658(in Chinese))
12 丁虎,胡超荣,陈立群等.轴向变速黏弹性Rayleigh梁非线性参数振动稳态响应.振动与冲击,2012,31(5):135-138(Ding Hu,Hu Chaorong,Chen Liqun,et al.Steady state response of nonlinear vibration of an axially accelerating viscoelastic Rayleigh beam.Journal of Vibration and Shock,2012,31(5):135-138(in Chinese))
13 Marynowski K.Dynamic analysis of an axially moving sandwich beam with viscoelastic core.Composite Structures,2012,94(9):2931-2936
14 唐有绮.轴向变速黏弹性Timoshenko梁的非线性振动.力学学报,2013,45(6):965-973(Tang Youqi.Nonlinear vibrations of axially accelerating viscoelastic Timoshenko beams.Chinese Journal of Theoretical and Applied Mechanics,2013,45(6):965-973(in Chinese))
15 Zhao FQ,Wang MM.Vibration analysis of an axially moving viscoelastic beam.Materials,Mechanical Engineering and Manufacture,Pts 1-3,2013,268(270):1177-1181
16 丁虎,严巧赟,陈立群等.轴向加速运动黏弹性梁受迫振动中的混沌动力学.物理学报,2013,(20):78-84(Ding Hu,Yan Qiaoyun,Chen Liqun,et al.Chaotic dynamics in the forced nonlinear vibration of an axially accelerating viscoelastic beam.Acta Physica Sinica,2013,(20):78-84(in Chinese))
18 王冬梅,张伟,李慕荣等.用微分求积法分析轴向移动黏弹性梁的非平面非线性振动.动力学与控制学报,2015,(1):23-27(Wang Dongmei,Zhang Wei,Li Murong,et al.Using DQM to analyze the nonplanar nonlinear vibrationa of an axially moving viscoelastic beam.Journal of Dynamics and Control,2015,(1):23-27(in Chinese))
19 Lin W,Qiao N.Vibration and stability of an axially moving beam immersed in fl uid.International Journal of Solids and Structures,2008,45(5):1445-1457
20 Ni Q,Li MW,Tang M,et al.Free vibration and stability of a cantilever beam attached to an axially moving base immersed in fl uid.Journal of Sound and Vibration,2014,333(9):2543-2555
21 Li MW,Ni Q,Wang L.Nonlinear dynamics of an underwater slender beam with two axially moving supports.Ocean Engineering,2015,108:402-415
22 Yan H,Ni Q,Dai HL,et al.Dynamics and stability of an extending beam attached to an axially moving base immersed in dense fl uid.Journal of Sound and Vibration,2016,383:364-383
23 Spelsberg-Korspeter G,Kirillov ON,Hagedorn P.Modeling and stability analysis of an axially moving beam with frictional contact.Journal of Applied Mechanics-Transactions of the ASME,2008,75(3):031001-10
24 Guo XX,Wang ZM.Thermoelastic Coupling vibration characteristics of the axially moving beam with frictional contact.Journal of Vibration and Acoustics-Transactions of the ASME,2010,132(5):051010-7
25 Zheng P,Yang TZ,Yang XD,et al.An approximate analytical solution of an axially moving beam subjected to harmonic and parametric excitations simultaneously.Proceedings of First International Conference of Modelling and Simulation,2008,5:340-345
26 Yan QY,Ding H,Chen LQ.Nonlinear dynamics of axially moving viscoelastic Timoshenkobeam under parametric and external excitations.Applied Mathematics and Mechanics-English Edition,2015,36(8):971-984
27 WangL,ChenHH,HeXD.ActiveH-in fi nitycontrol ofthe vibration of an axially moving cantilever beam by magnetic force.Mechanical Systems and Signal Processing,2011,25(8):2863-2878
28 Zhang YW,Zhang Z,Chen LQ,et al.Impulse-induced vibration suppression of an axially moving beam with parallel nonlinear energy sinks.Nonlinear Dynamics,2015,82(1):61-71
29 Ghayesh MH,Kazemirad S,Amabili M.Coupled longitudinaltransverse dynamics of an axially moving beam with an internal resonance.Mechanism and Machine Theory,2012,52:18-34
30 Park S,Yoo HH,Chung J.Vibrations of an axially moving beam with deployment or retraction.AIAA Journal,2013,51(3):686-696
31 Yang XD,Zhang W.Nonlinear dynamics of axially moving beam with coupled longitudinal-transversal vibrations.Nonlinear Dynamics,2014,78(4):2547-2556
32 Stylianou M,Tabarrok B.Finite element analysis of an axially moving beam,Part I:time integration.Journal of Sound and Vibration,1994,178(4):433-453
33 Chang JR,Lin WJ,Huang CJ,et al.Vibration and stability of an axially moving Rayleigh beam.Applied Mathematical Modelling,2010,34(6):1482-1497
34 Ghayesh MH,Amabili M.Nonlinear vibrations and stability of an axially moving Timoshenko beam with an intermediate spring support.Mechanism and Machine Theory,2013,67:1-16
35 Park S,Chung JT.Dynamic analysis of an axially moving fi nitelength beam with intermediate spring supports.Journal of Sound and Vibration,2014,333(24):6742-6759
36 Oz HR,Pakdemirli M,Boyaci H.Non-linear vibrations and stability of an axially moving beam with time-dependent velocity.International Journal of Non-Linear Mechanics,2001,36(1):107-115
37 Al-Bedoor BO,Khulief YA.An approximate analytical solution of beam vibrations during axial motion.Journal of Sound and Vibration,1996,192(1):159-171
38 Matsuzaki Y.Vibration of a cantilevered beam during deployment and retrieval:analysis and experiment.Smart Materials&Structures,1998,4(4):334-339
39 Zhang H,Chen L.Vibration of an axially moving string supported by a viscoelastic foundation.Acta Mechanica Solida Sinica,2016,29(3):221-231
AN EFFICIENT DYNAMIC MODELING METHOD OF AN AXIALLY MOVING CANTILEVER BEAM AND FREQUENCY RESPONSE ANALYSIS1)
Hua Hongliang Liao Zhenqiang2)Zhang Xiangyan
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing210094,China)
The dynamics of the axially moving beam has wide application in engineering,such as robot manipulators,machine tools and gun barrel,et al.Computing the dynamic response of axially moving beam is an important method to evaluate the dynamic performance and fi nally the structure design.The time-varying motion equations of the axially movingcantileverbeamarederivedusingtheRayleigh-RitzmethodandLagrange’sequation.Thepowerseriesfunctionis used to construct the trial function to solve the dynamic problem.Due to the good integral and di ff erential performance of power series function,the derivation is easy to be carried out in the form of matrix.In this way,the symbolic computation software can generate the MATLAB program directly.And the generated MATLAB program can be used to conduct the dynamic computation with few modi fi cations,because the basic data unit of MATLAB is matrix.The overall process is efficiency and the time from dynamic modeling to computation is greatly reduced.Through four sets of numerical examples,the computational accuracy of the presented method is validated by comparing the dynamic responses with those from previous literatures.Then,the e ff ects of fi tting order of the power series function on computational accuracy are discussed.And the principle to select the fi tting order of the power series function to achieve good convergence and computational accuracy is given.Based on the dynamic model,the e ff ects of axial motion frequency on transverse vibration are studied.The e ff ects of axial vibration amplitude on the frequency response characteristic are explored.And the di ff erence between considering gravity and neglecting gravity e ff ect are compared.
computational dynamics,power series basis function,frequency response analysis,axially moving beam
O313
A doi:10.6052/0459-1879-17-182
2017–05–16 收稿,2017–08–07 录用,2017–08–10 网络版发表.
1)国家自然科学基金资助项目(51375241).
2)廖振强,教授,主要研究方向:自动武器发射动力学.E-mail:huahl123@126.com
华洪良,廖振强,张相炎.轴向移动悬臂梁高效动力学建模及频率响应分析.力学学报,2017,49(6):1390-1398
Hua Hongliang,Liao Zhenqiang,Zhang Xiangyan.An efficient dynamic modeling method of an axially moving cantilever beam and frequency response analysis.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1390-1398
