梯度波阻板的地基振动控制研究1)
2017-12-18周凤玺
马 强 周凤玺,2) 刘 杰
*(兰州理工大学土木工程学院,兰州730050)
†(兰州交通大学交通运输学院,兰州730070)
梯度波阻板的地基振动控制研究1)
马 强*周凤玺*,2)刘 杰†
*(兰州理工大学土木工程学院,兰州730050)
†(兰州交通大学交通运输学院,兰州730070)
波阻板(wave impeding block,WIB)隔振体系是一种有效的振动污染治理措施,虽逐渐被应用在工程实际中,但以往的研究多集中于单相固体均质材料的情形,而对材料特性沿空间连续变化的非均匀固体材料的波阻板隔振性能的研究相对较少.基于功能梯度材料(functionally graded material,FGM)特点,本文提出了以功能梯度波阻板作为隔振屏障的一类新型的地基振动控制体系.考虑在弹性地基内部设置梯度波阻板,基于线弹性理论,利用傅里叶积分变换,根据Helmholtz矢量分解原理,建立了弹性地基在动载荷作用下的回传射线矩阵法(reverberation ray matrix method,RRMM)计算列式.假设梯度波阻板的物理力学性质沿深度方向按幂函数连续变化,采用数值傅里叶逆变换获得了弹性地基的位移和应力等物理量的数值解.通过数值算例,与单相固体均质波阻板进行了对比,并分析讨论了梯度波阻板的材料梯度因子、埋深以及梯度波阻板厚度等物理力学参数对地基隔振性能的影响规律.结果表明,梯度波阻板能有效降低振动的振幅,与单相固体均质波阻板相比,梯度波阻板具有更好的减振隔振效果.地基的位移幅值和应力幅值随着梯度因子的增大而减小.梯度波阻板的隔振效果随着波阻板厚度的增大而提高,而随着梯度波阻板埋深的增大而降低.
地基振动控制,弹性地基,动力响应,梯度波阻板,回传射线矩阵法
引言
随着城镇化建设和现代工业的迅速发展,各种环境振动引起的环境污染问题日益频繁,导致环境振动的因素越来越多,振源强度越来越大.另一方面,随着人们生活水平的提高,人们对生活环境和工作环境的质量要求越来越高,对振动的限制越来越严格,环境振动及其治理已经成为岩土工程的研究热点之一.因此,对环境振动产生的原因、传播过程和振动规律进行研究,找到减振隔振的有效方法,是环境振动研究的根本目的,具有重要的工程意义和实用价值.
地基振动由于振源位置、振源类型以及地基物理力学性质的不同而产生不同的波场特性,其振动的传播过程和衰减规律也不相同.对于地基的动力行为以及波的传播特性问题,国内外学者从载荷类型、地基特征(包括材料特性和边界条件)等多方面进行了分析并取得了一系列重要的研究成果[1-6].然而关于地基振动的控制问题则研究较少.自Woods[7]通过一些现场原位试验,研究了近场主动隔振和远场被动隔振的效果,并且提出了一个评判屏障隔振效果的重要参数 (振幅衰减系数)以来,国内外学者对连续屏障和非连续屏障的减振隔振效果进行了一系列的研究工作[8-16].除屏障隔振外,Chouw等[17]最先提出一种在地基中人为设置波阻板(wave impedance block,WIB)进行减振隔振的方法,随后他们采用二维频域边界元法,分析了WIB主动隔振和被动隔振效果,获得了WIB的被动隔振效果好于填充沟的结果.Peplow等[18]采用边界积分方程法研究了二维双层地基波阻板主动隔振的效果.Takemiya等[19-20]对基岩上单一土层中群桩基础激振时波阻板的隔振效果进行研究,结果表明采用波阻板进行隔振是有效的,并首次提出了一种蜂窝状波阻板(honeycomb WIB,HWIB)隔振措施,对高架铁路桩基的HWIB隔振效果进行了现场试验,得到了令人满意的结果.高广运等[21-22]建立了层状介质中土与结构动力相互作用的半解析边界元法模型,分析了二维和三维层状地基中波阻板的隔振效果.针对三维竖向非均匀和饱和地基模型,在轨道交通载荷作用下,高广运等[23-24]分别对竖向非均匀地基和饱和地基中波阻板的隔振性能进行了研究.基于含液饱和多孔介质中的流--固耦合作用,周凤玺等[25]研究了含液饱和多孔介质波阻板的隔振性能,结果表明基于含液饱和多孔波阻板的地基隔振体系更具优越性.基于改进的三维边界有限元模型,Gao等[26]研究了饱和土体中波阻板的隔振效果,分析了土--地基--波阻板相互作用的问题.
自功能梯度材料的概念被提出以来[27],对材料特性沿空间连续变化的非均匀固体材料力学行为的研究得到了广泛的关注[28-33].功能梯度材料是一种新型复合材料,其具有空间连续梯度变化的微观结构,可引起材料属性的梯度变化,实现材料内部功能的渐变,具有缓和热应力、避免或降低层间应力集中和可设计性良好等优点[34].以梯度材料作为隔振屏障,本文提出了一类新型的波阻板地基隔振体系.文章的第1节建立了弹性地基内部设置梯度波阻板的数学模型,并利用傅里叶(Fourier)积分变换,根据亥姆霍兹(Helmholtz)矢量分解原理,推导获得了土体动力问题的位移、应力在Fourier变换域中的通解.第2节采用回传射线矩阵法获得了地基表面受到条形荷载作用下地基中任一点处的位移和应力的计算列式.第3节通过数值算例与单相固体均质波阻板的隔振性能进行了对比,并分析讨论了梯度波阻板的材料梯度因子、埋深以及梯度波阻板厚度等物理力学参数对地基隔振性能的影响规律.第4节为结论.
1 土体力学问题的数学模型
在二维弹性地基中设置一个单相固体梯度波阻板,如图1所示.二维弹性地基厚度H=H1+hw+H2,其中梯度波阻板厚为hw,且波阻板上表面所处的位置在x3方向距离地基表面为H1,下表面所处的位置在x3方向距离基岩的下部土层的厚度为H2,载荷幅值为q0,分布长度为2l.
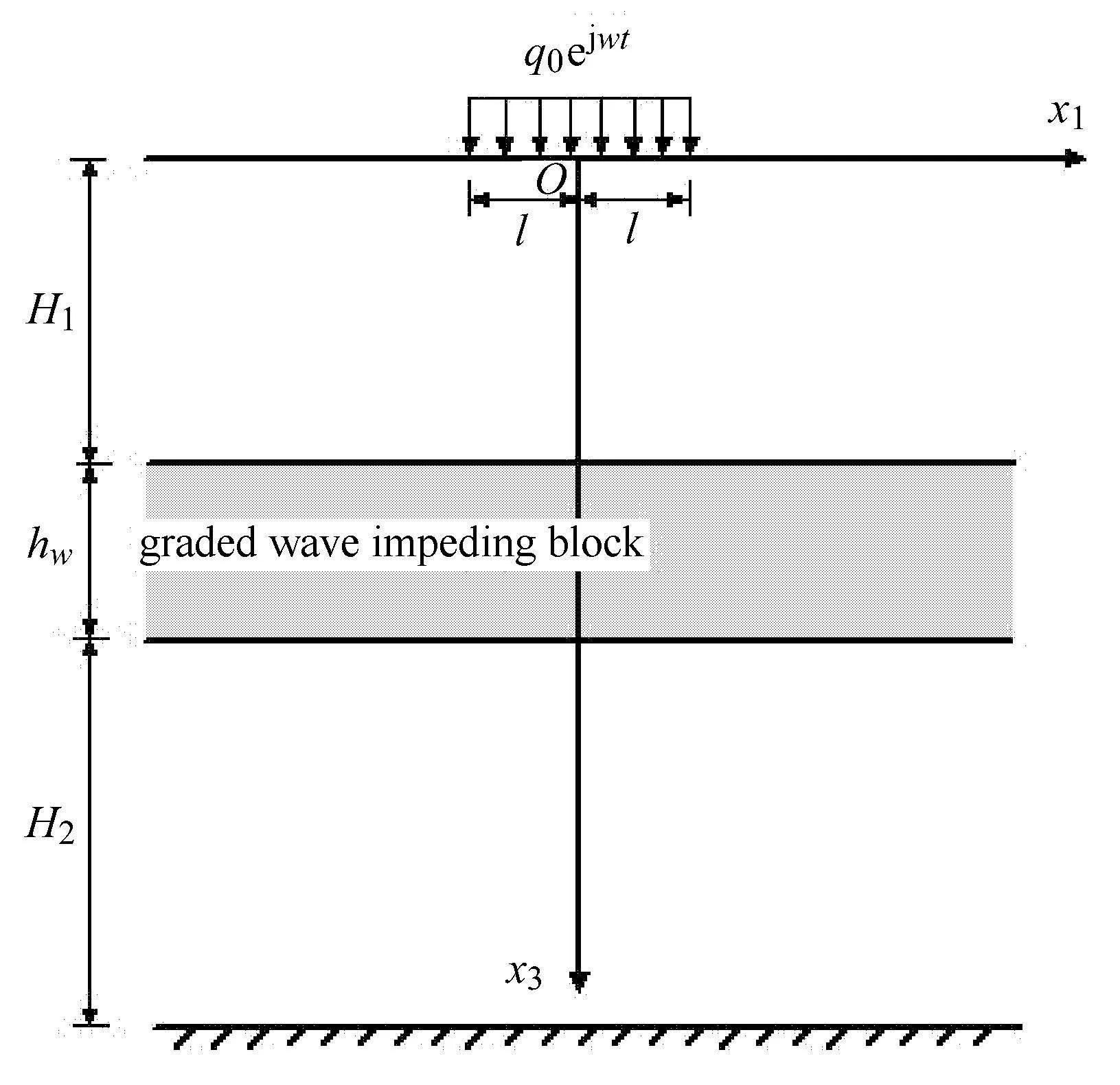
图1 条形载荷下弹性地基示意图Fig.1 The elastic foundation under strip harmonic load
各向同性的线弹性单相连续固体介质的基本方程如下:
物理方程为
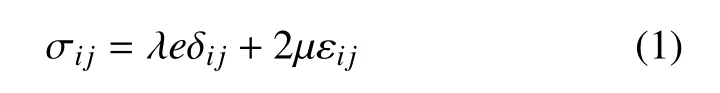
几何关系为
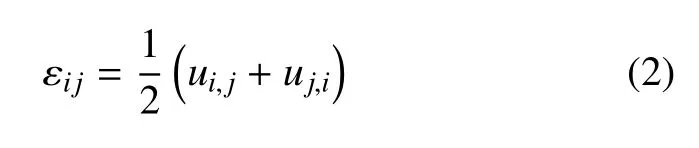
运动方程为

其中,σij为单相弹性固体介质的总应力分量(i,j=1,3);δij表示克罗内克 (Kroeneker)符号;e=ui,i;ui为固体位移;λ和µ为固体骨架拉姆(Lame)弹性常数;εij为固体骨架的应变;ρ为土体密度.
由式(1)∼式(3)可得各向同性的线弹性单相连续固体介质的控制方程为

考虑到简谐载荷作用,土体骨架位移可写成
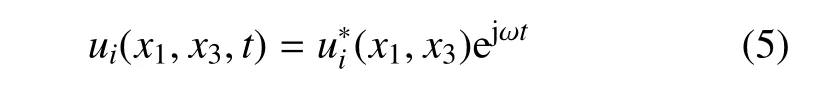
为了方便,后面的推导过程略去星号.根据亥姆霍兹矢量分解定理,位移矢量u(x1,x3)可以用势函数φ和ψ表示为

对空间变量x1进行Fourier变换
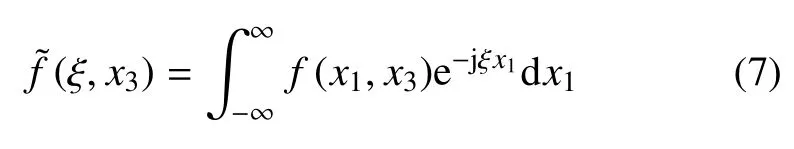
将式(5)∼式(7)代入方程(4)中,经过Fourier变换整理可得

因此,常微分方程(8)和方程(9)在傅里叶变换域中的表达式为
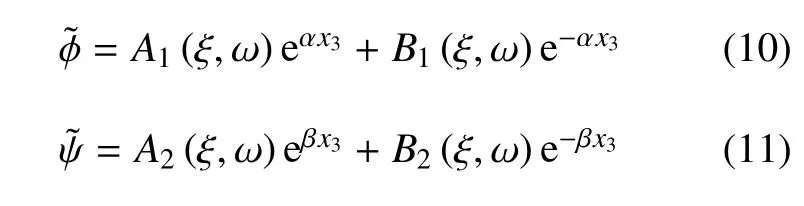
在直角坐标系(x1,x3)中,各位移分量可用位移势函数φ和ψ表示为

结合式(10)∼式(13)以及式(1),最终可得到土体动力问题的位移、应力在傅里叶变换域中的通解为
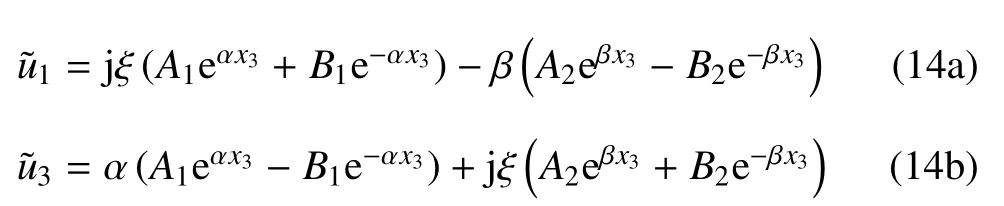
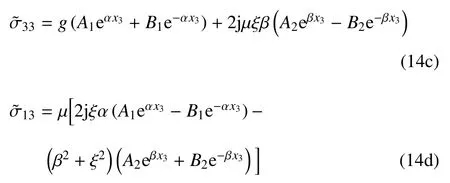
2 回传射线矩阵法求解
对于在二维弹性地基中设置的单相梯度波阻板,由于单相梯度波阻板材料的非均匀性,导致土体动力问题的控制方程为变系数偏微分方程,一般情况下很难获得解析解.为此,通常将非均匀材料沿材料特性变化方向简化为许多均匀材料薄层,如图2所示,层数N由问题所要求的精度决定.对于简化以后的层合模型,常用的分析方法是传递矩阵法[35],但基于传递矩阵列式的数值计算会出现数值不稳定问题.近年来,Pao等[36]提出回传射线矩阵法的波动模型,并将其应用到层状介质中,取得了很好的效果[37-38],该模型在稳态和早期瞬态响应计算中具有结果精确、数值稳定、列式统一等优点,是一种有效的动力学分析方法.周凤玺等[39]建立了一维梯度非均匀饱和多孔土体在动载荷作用下的回传射线矩阵法计算列式,结果表明回传射线矩阵法对梯度非均匀饱和土动力响应分析具有很好的适用性,其计算稳定,有利于求解复杂的波动问题.回传射线矩阵法的关键在于对每个单元/层建立两个局部坐标系(一对对偶坐标系),一个位于该层顶面,另一个位于该层底面.图3绘出了第i层的对偶坐标系,表示局部坐标系位于第i层,并且指向第i+1层.通过对偶坐标系的变换,可以有效地避免计算过程中的数值问题.

图2 层和模型示意图Fig.2 The approximate laminate model

图3 局部坐标示意图Fig.3 Dual local coordinates at the interface
2.1 散射关系

根据回传射线矩阵法的基本思路,在对偶局部坐标系下的所有节点建立力的平衡和位移协调关系,以i(i−1)和i(i+1)的共同界面i为例,其连续条件为
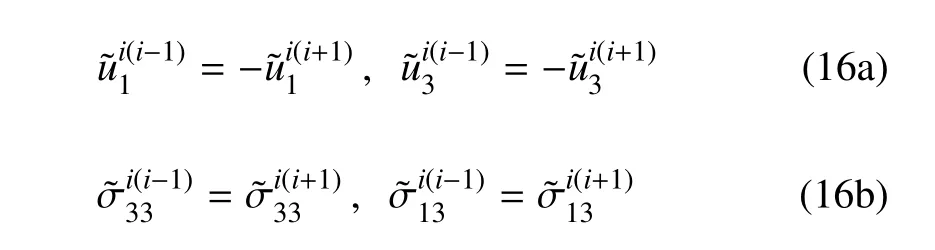
利用式(15)和式(16),整理后可得

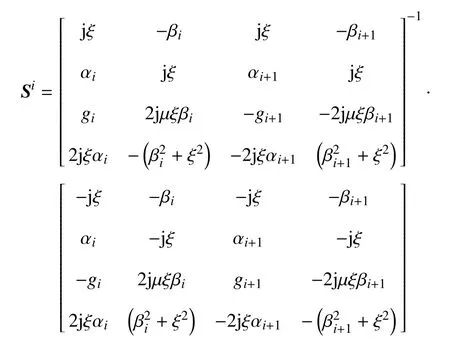
考虑弹性地基表面受条形均布荷载作用,底面固定的边界条件为
在x3=0处
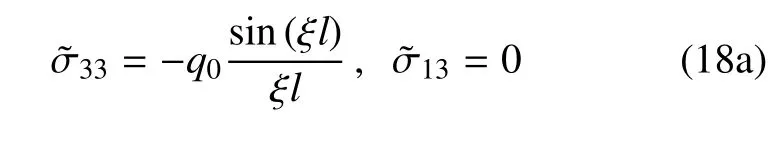
在x3=H处

利用式(15)和式(18),整理后可得

式中

合并方程(17)和方程(19)可得

其中

向量A和B一共含有8N个未知量,而方程(20)只提供了4N个方程.为求得所有的未知量,须再补充一组方程.
2.2 相位关系和回传射线矩阵
同一点处的物理量可以在一对对偶局部坐标系下同时表示,因此,两个表达式必须等价.对于竖向位移˜u3存在下述关系
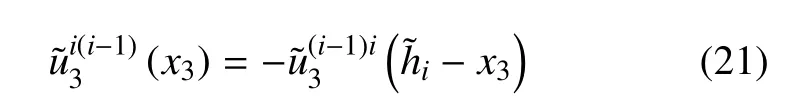
将式(15b)代入式(21)可得到

引入新矢量
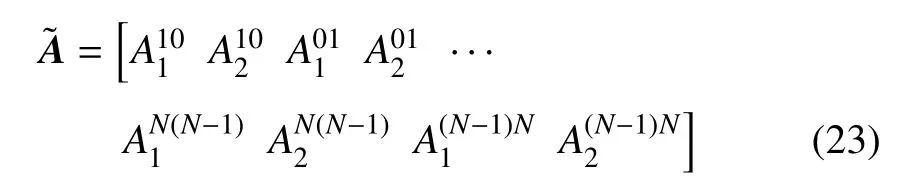
结合式(20),式(22)∼式(23)可得

式中P为整体相位矩阵,定义为

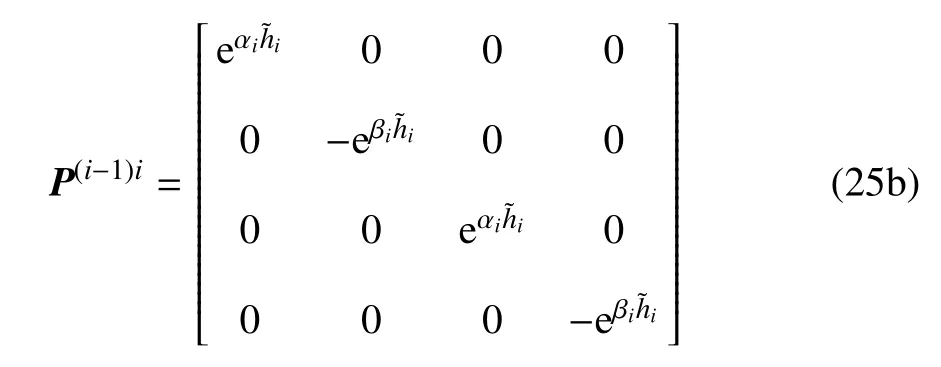
U为整体置换矩阵,定义为
将式(24)代入式(20),最终可得

式中R=SPU称为回传射线矩阵,I为单位矩阵.
利用式(27)求出A和B后,结合式(15),就可以获得在频域中地基中任一点处的位移和应力等物理量,然后利用Fourier逆变换可以得到空间域上相应的物理量.
3 数值算例
考虑梯度波阻板的材料特性沿厚度方向按幂函数变化,则有
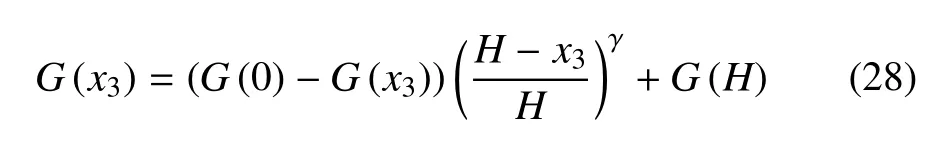
式中,G(x3)为在x3处的E,υ,ρ等物理力学参数,其中,E为弹性模量,υ为泊松比;γ为梯度因子,不同的γ值代表非均匀程度不同的波阻板.可知当γ=0时梯度材料即为均质材料,其物理力学性质为表面处的材料特性;当γ→∞时,此时梯度材料参数趋于梯度板底面的均匀材料.
在数值计算中,选取弹性地基的物理力学参数如下:弹性模量E0=98MPa,泊松比ν=0.3,密度ρ0=1.884g/cm3.计算中取均布载荷幅值q0=1kPa,频率ω=25rad/s,l=0.5m.梯度波阻板的物理力学参数为:在x3=H1处即梯度波阻板表面处E1=6.5MPa,ρ1=1.4g/cm3,ν=0.3. 在x3=H1+hw处即梯度波阻板底面处E2=650MPa,ρ2=2.458g/cm3,泊松比ν=0.33.为了简化起见,假设梯度波阻板各物理力学参数具有相同的变化趋势,也就是说各物理力学参数沿深度按同样的梯度因子变化.由于被积函数表达式较为复杂,因此很难得出Fourier逆变换的封闭形式解,本文采用FFT方法完成Fourier逆变换,波数的离散点为2048,空间计算区间为200m.
为了考虑不同分层数N对计算结果的影响,表1给出了当γ=0和γ=1时不同分层数N的情形下地基表面条形荷载中点处的竖向位移值.从表1中可以看出,当分层数N选取100时足以满足计算精度要求.

表1 不同层数N对竖向位移计算结果的影响Table 1 The vertical displacement calculated by RRMM with di ff erent numbers of layers N
考虑上覆土厚度H1=4m,波阻板厚度hw=4m,下部土层厚度H1=10m,图4给出了在地基表面(x3=0)处竖向位移沿水平方向的变化曲线,比较了弹性地基中设置单相固体均质波阻板(即γ=0时)、梯度波阻板两种不同情形.由图4中可以看出,由于波阻板的设置改变了弹性地基中竖向位移的振动相位,并且与单相固体均质波阻板相比,梯度波阻板使竖向位移幅值降低显著,具有更好的减振隔振效果.

图4 地基表面竖向位移变化曲线Fig.4 Variations of vertical displacement at the ground surface
为了反映梯度因子对梯度波阻板隔振效果的影响,其他参数不变,图5和图6给出了在不同材料梯度因子的情形下,弹性地基表面(x3=0)处竖向位移u3的实部沿水平方向的变化曲线和弹性地基底面(x3=H)处正应力σ33沿水平方向的变化曲线.从图5和图6可以看出,当γ=0即波阻板为弹性均质材料时,地基的位移幅值和应力幅值最大.随着γ的增大,条形荷载中点下位移幅值和应力幅值都随之减小,这主要是由于梯度因子γ的增大,意味着抵抗变形能力强的层底材料增多,从而引起位移幅值和应力幅值的降低.从图5和图6中还可以看出,无论是位移分量还是应力分量,在水平方向的振动频率随着梯度因子γ的变化而变化.

图5 地基表面竖向位移随γ的变化曲线Fig.5 Variations of vertical displacement at the ground surface with γ

图6 地基底面正应力随γ的变化曲线Fig.6 Variations of normal stress at the ground bottom surface with γ
对同样的梯度波阻板反向布置,即上表面弹性模量大于下表面,为了反映此种情况下梯度因子对梯度波阻板隔振效果的影响,其他参数不变,图7给出了在不同材料梯度因子的情形下,弹性地基表面(x3=0)处竖向位移u3的实部沿水平方向的变化曲线.从图7可以发现,与上表面弹性模量小于下表面的情况正好相反,随着γ的增大,条形荷载中点下竖向位移幅值随之增大,但是竖向位移在水平方向的振动频率依然随着梯度因子γ的变化而变化.
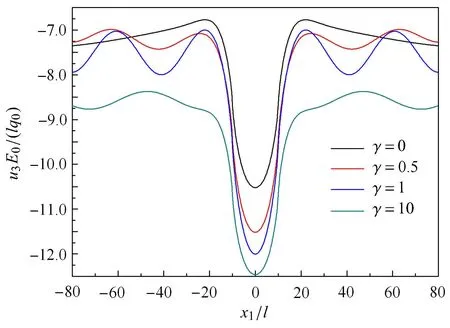
图7 地基表面竖向位移随γ的变化曲线Fig.7 Variations of vertical displacement at the ground surface with γ
为了分析梯度波阻板的埋深对地基隔振效果的影响,图8绘出了在hw=4m时梯度波阻板埋深从H1=0.5,1,2,3,4m逐渐增大时,地基表面竖向位移沿水平方向的变化曲线.
从图8可以看出,随着梯度板埋深的增大,在施加载荷附近的竖向位移先减小后增大,表明不同梯度板埋深即不同上覆土层厚度的隔振效果差别很大;而远离载荷施加位置的竖向位移,随着梯度板埋深的变化,仅当梯度板埋深等于1m时,竖向位移最大,其余梯度板埋深不同时竖向位移有一定的差异,但不显著.以上现象与文献[21,40]中波阻板埋深不同时的竖向位移的表现相似.因为波阻板就是利用地基存在截止频率的原理隔振,而截止频率的大小与上覆土层的厚度,即与波阻板的埋深成反比[21],所以要想取得理想的隔振效果,就必须使上覆土层的厚度较小,即波阻板的埋深必须较小.结合图8,在梯度波阻板埋深H1按0.5,1,2,3,4m增大的情况下,综合比较施加载荷附近和远离载荷施加位置的竖向位移的大小,只有在梯度板埋深H1=0.5m时会产生稳定的隔振效果,这说明尽可能选择梯度波阻板较小的埋深其隔振效果越好.
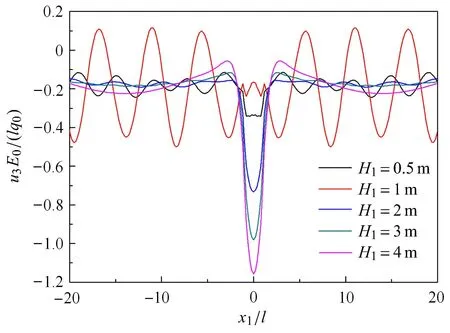
图8 地基表面竖向位移随梯度波阻板埋深的变化曲线Fig.8 Variations of vertical displacement at the ground surface with depth
为了分析梯度波阻板的厚度对地基隔振效果的影响,在H1=4m时图9绘出了梯度波阻板板厚hw分别为1,2,3,4m时对地基表面竖向位移的影响.从图9可以看出,无论是施加载荷附近的竖向位移还是远离载荷施加位置的竖向位移,梯度波阻板的隔振减振效果都随着波阻板厚度的增大而增大.当梯度波阻板厚度hw6 2m时,随着梯度波阻板厚度的增大,其隔振效果迅速增大;当波阻板厚度hw>2m时,随着梯度波阻板厚度的增大,梯度波阻板隔振体系的隔振效果虽然也增大,但是竖向位移幅值提高的幅度却逐渐减小.
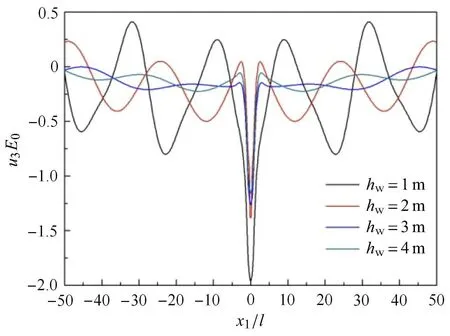
图9 地基表面竖向位移随板厚的变化曲线Fig.9 Variations of vertical displacement at the ground surface with thickness
4 结论
基于功能梯度材料,本文提出了以梯度波阻板作为隔振屏障的新型地基隔振体系.利用Fourier积分变换,通过Helmholtz矢量分解原理,推导获得了土体动力问题的位移、应力在Fourier变换域中的通解.采用回传射线矩阵法和快速傅里叶逆变换获得了时域中地基中任一点处的位移和应力的计算.通过大量的数值结果,研究了梯度波阻板的材料梯度因子、埋深以及梯度波阻板厚度等物理力学参数对地基隔振性能的影响规律,得到了以下结论:(1)梯度材料的地基隔振屏障相对于单相固体均质波阻板是一类更具有可设计性的隔振体系,具有更好的减振隔振效果;(2)当梯度波阻板上表面弹性模量小于下表面时,地基的位移幅值和应力幅值随着梯度因子的增大而减小,反之则增大;(3)梯度波阻板的隔振效果随着波阻板厚度的增大而增大,此外应保证梯度波阻板具有较小的埋深,才能得到理想的隔振效果.
1 Sneddon IN.The stress produced by a pulse of pressure moving along the surface of a semi-in fi nite solid.Rendiconti del Circolo Matematico di Palermo,1952,2:57-62
2 Zienkiewicz OC,Chang CT,Beettss P.Drained,undrained,consolidation and dynamic behavior assumptions in soils.Geotechnqiue,1980,30:385-395
3 陈远国,金波.移动简谐荷载作用下多孔地基的动力响应.中国科学G辑,2008,38(3):250-259(Chen Yuanguo,Jin Bo.Dynamic response of a poroelastic stratum to moving oscillating load.Science in China.Series G,2008,38(3):250-259(in Chinese))
4 周凤玺,曹永春,赵王刚.移动荷载作用下非均匀地基的动力响应分析.岩土力学,2015,36(7):2027-2033(Zhou Fengxi,Cao Yongchun,Zhao Wanggang.Analysis of dynamic response of inhomogeneoussubgradeundermovingloads.RockandSoilMechanics,2015,36(7):2027-2033(in Chinese))
5 胡安峰,李怡君,贾玉帅等.埋置移动荷载作用下成层饱和地基的动力响应.工程力学,2016,33(12):44-62(Hu Anfeng,Li Yijun,Jia Yushuai,et al.Dynamic response of a layered saturated ground subjected to a buried moving load.Engineering Mechanics,2016,33(12):44-62(in Chinese))
6 Bagno AM.Wave propagation in an elastic layer interacting with a viscous liquid layer.International Applied Mechanics,2016,52(2):133-139
7 Woods RD.Screening of surface waves in soils.Journal of the Soil Mechanics and Foundations Division,1968,94(4):95l-979
8 Ahmad S,Al-Huasaini TM,Fishman KL.Investigation on active isolation of machine foundations by open trenches.Journal of Geotechnical Engineering,1996,122(6):454-461
9 Kattis SE,Polyzos D,Brjkos DE.Vibration isolation by a row of piles using a 3-D frequency domain BEM.International Joumal for Numerical Methods in Engineering,1999,46(5):713-728
10 Huang JH,Xiao XZ,Dong XH,et al.Barrier vibration isolation to work-place vibration and its in fl uence on uneven subsidence of pillar foundation.Wuhan University Journal of Natural Sciences,2002,7(4):445-450
11 高广运,李志毅,邱畅.填充沟屏障远场被动隔振三维分析.岩土力学,2005,26(8):1184-1188(Gao Guangyun,Li Zhiyi,Qiu Chang.Three-dimensional analysis of in- fi lled trench as barriers for isolating vibration in far fi led.Rock and Soil Mechanics,2005,26(8):1184-1188(in Chinese))
12 With C,Bahrekazemi M,Bodare A.Wave barrier of lime-cement columns against train-induced ground-borne vibrations.Soil Dynamics and Earthquake Engineering,2009,29:1027-1033
13 Katsuya I,Ryota S,Tomihiro H et al.Systematic analyses of vibration noise of a vibration isolation system for high-resolution scanning tunneling microscopes.Review of Scienti fi c Instruments,2011,82(8):702-707
14 徐平,周新民,夏唐代.应用屏障进行被动隔振的研究综述.地震工程学报,2015,37(1):88-93(Xu Ping,Zhou Xinmin,Xia Tangdai.Review on passive vibration isolation using barriers.Chinese Earthquake Engineering Journal,2015,37(1):88-93(in Chinese))
15 巴振宁,王靖雅,梁建文.层状地基中隔振沟对移动列车荷载隔振研究——2.5维IBEM方法.振动工程学报,2016,29(5):860-873(Ba Zhenning,Wang Jingya,Liang Jianwen.Reduction of train induced vibrations by using a trenchin a layered foundation.Journal of Vibration Engineering,2016,29(5):860-873(in Chinese))
16 刘中宪,王少杰.非连续群桩屏障对平面P、SV波的隔离效应:二维宽频带间接边界积分方程法模拟.岩土力学,2016,37(4):1195-1207(Liu Zhongxian,Wang Shaojie.Isolation e ff ect of discontinuous pile-group barriers on plane P and SV waves:Simulation based on 2D broadband indirect boundary integration equation method.Rock and Mechanics,2016,37(4):1195-1207(in Chinese))
17 Chouw N,Le R,Schmid G.An approach to reduce foundation vibrations and soil waves using dynamic transmitting behavior of a soil layer.Bauingenieur,1991,66:215-221
18 Peplow AT,Jones CJC,Petyt M.Surface vibration propagation over a layered elastic half-space with an inclusion.Applied Acoustics,1999,56:283-296
19 Takemiya H,Fujiwara A.Wave propagation/impediment in a stratum and wave impeding block(WIB)measured for SSI response reduction.Soil Dynamics and Earthquake Engineering,1994,13:49-61
20 Takemiya H.Field vibration mitigation by honeycomb WIB for pile foundations of a high-speed train viaduct.Soil Dynamics and Earthquake Engineering,2004,24:69-87
21 高广运,李伟.二维地基波阻板隔振分析.地震工程与工程振动,2005,24(2):130-135(Gao Guangyun,Li Wei.2D analysis of ground vibration isolation using wave impeding block.Earthquake Engineering and Engineering Vibration,2005,24(2):130-135(in Chinese))
22 高广运,张博,李伟.层状和竖向非均匀地基中水平--摇摆耦合激振波阻板三维隔振分析.岩土力学,2012,33(2):349-353(Gao Guangyun,Zhang Bo,Li Wei.3D analysis of vibration isolation using wave impeding block in layered and vertical heterogeneous foundation under horizontal-rocking coupled excitation.Rock and Soil Mechanics,2012,33(2):349-353(in Chinese))
23 高广运,陈功奇,张博.列车荷载下竖向非均匀地基波阻板主动隔振分析.振动与冲击,2013,32(22):57-62(Gao Guangyun,Chen Gongqi,Zhang Bo.Active vibration isolation using WIB in nonuniform ground under train loadings.Journal of Vibration and shock,2013,32(22):57-62(in Chinese))
24 高广运,王非,陈功奇.轨道交通荷载下饱和地基中波阻板主动隔振研究.振动工程学报,2014,27(3):433-440(Gao Guangyun,Wang Fei,Chen Gongqi.Active vibration isolation of the saturated ground with wave impedence block inside and under the load of the travelling train.Journal of Vibration Engineering,2014,27(3):433-440(in Chinese))
25 周凤玺,马强,赖远明.含液饱和多孔波阻板的地基振动控制研究.振动与冲击,2016,35(1):96-105(Zhou Fengxi,Ma Qiang,Lai Yuanming.Ground vibration control with fl uid-saturated porous wave impeding blocks.Journal of Vibration and Shock,2016,35(1):96-105(in Chinese))
26 Gao GY,Chen J,Gu XQ,et al.Numerical study on the active vibration isolation by wave impeding block in saturated soils under vertical loading.Soil Dynamics and Earthquaake Engineering,2017,93:99-112
27 Hirai H,Chen L.Recent and prospective development of FGM in Japan.Materials Science Frames,1999,308:509-514
28 仲政,吴林志,陈伟球.功能梯度材料与结构的若干力学问题研究进展.力学进展,2010,40(5):528-541(Zhong Zheng,Wu Linzhi,Chen Weiqiu.Progress in the study on mechanics problems of functionally graded materials and structures.Advances in Mechanics,2010,40(5):528-541(in Chinese))
29 雷鸣,廖红建,黄理兴等.应力波在功能梯度土介质中传播的特性研究.岩石力学与工程学报,2005,24(s1):4798-4804(Lei Ming,Liao Hongjian,Huang Lixing,et al.Study on characters of stress wave propagation in functionally graded soil.Chinese Journal of Rock Mechanics and Engineering,2005,24(s1):4798-4804(in Chinese))
30 程站起,刘建.基于近场动力学的功能梯度材料动态断裂分析.应用力学学报,2016,33(4):634-639(Cheng Zhanqi,Liu Jian.Fracture analysis of functionally graded materials under impact loading based on peridynamics.Chinese Journal of Applied Mechanics,2016,33(4):634-639(in Chinese))
31 许新,李世荣.功能梯度材料微梁的热弹性阻尼研究.力学学报,2017,49(2):308-316(Xu Xin,Li Shirong.Analysis of thermoelastic damping for functionally graded material micro-beam.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):308-316(in Chinese))
32 夏巍,冯浩成.热过屈曲功能梯度壁板的气动弹性颤振.力学学报,2016,48(3):609-614(Xia Wei,Feng Haocheng.Aeroelastic flutter of post-buckled functionally graded panels.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):609-614(in Chinese))
33 高效伟,郑保敬,刘健.功能梯度材料动态断裂力学的径向积分边界元法.力学学报,2015,47(5):868-873(Gao Xiaowei,Zheng Baojing,Liu Jian.Dynamic fracture analysis of functionally graded materials by radial integration BEM.Chinese Journal of Theoretical and Applied Mechanics,2015,47(5):868-873(in Chinese))
34 徐坤,陈美霞,谢坤.正交各向异性功能梯度材料平板振动分析.噪声与振动控制,2016,36(4):14-20(Xu Kun,Chen Meixia,Xie Kun.Vibration analysis of orthotropic functionally graded plates.Noise and Vibration Control,2016,36(4):14-20(in Chinese))
35 赵宇昕,陈少林.关于传递矩阵法分析饱和成层介质响应问题的讨论.力学学报,2016,48(5):1145-1158(Zhao Yuxin,Chen Shaolin.Discussion on the matrix propagator method to analyze the response of saturated layered media.Chinese Journal of Theoretical and Applied Mechanics,2016,48(5):1145-1158(in Chinese))
36 Pao H,Ken DC,Howard SM.Dynamic response and wave propaga-tion in plane trusses and frames.American Institute of Aeronautics and Astronautics,1999,37:594-603
37 Pao YH,Su XY,Tian JY.Reverberation matrix method for propagation of sound in a multilayered liquid.Journal of Sound and Vibration,2000,230:743-760
38 SuXY,TianJY,PaoYH.Applicationofthereverberation-raymatrix to the propagation of elastic waves in a layered solid.International Journal of Solids and Structures,2002,39:5447-5463
39 周凤玺,赖远明.梯度饱和土瞬态响应分析.力学学报,2012,44(5):943-947(Zhou Fengxi,Lai Yuanming.Transient dynamic analysis of grandient fl uid-saturated soil.Chinese Journal of Theoretical and Applied Mechanics,2012,44(5):943-947(in Chinese))
40 高广运,冯世进,李伟等.二维层状地基波阻板隔振分析.振动工程学报,2007,20(2):175-179(Gao Guangyun,Feng Shijin,Li Wei,et al.2-D analysis of vibration isolation by wave impeding block in layered ground.Journal of Vibration Engineering,2007,20(2):175-179(in Chinese))
ANALYSIS OF GROUND VIBRATION CONTROL BY GRADED WAVE IMPEDING BLOCK1)
Ma Qiang*Zhou Fengxi*,2)Liu Jie†
*(School of Civil Engeering,Lanzhou University of Technology,Lanzhou730050,China)
†(School of Traffic and Transportation,Lanzhou JiaoTong University,Lanzhou730070,China)
Wave impeding block(WIB)vibration isolation system as an e ff ective measure for vibration pollution control is applied in practical engineering gradually,but the previous studies mostly focused on the single-phase solid homogenous materials,few research have been on the vibration isolation performance of wave impeding block with materials properties that have a continuous variation along space relatively.Based on the functionally graded material,a new type of foundation vibration isolation system is proposed.Considering setting the graded wave impeding block in the elastic foundation which subjected to surface strip harmonic load,using the Fourier transform and Helmholtz vector decomposition,the calculation formula of reverberation ray matrix method(RRMM)is established for two-dimensional transient response of elastic foundation based on the line elastic theory.Assuming that the material properties of graded wave impeding block have an exponential law distribution along the thickness-coordinate,by using numerical inverse Fourier transformation,the displacement and the stress are obtained.Via numerical examples,the e ff ectiveness of vibration isolation of graded wave impeding block is compared to conventional single phase solid homogenous wave impeding block,and the in fl uences of physical and mechanical parameters including the gradient factor,the depth and the thickness of graded wave impeding block are analyzed.The results show that the graded wave impeding block can e ff ectively reduce the vibration amplitude,and compared with the single phase solid homogenous wave impeding block isolation system,graded wave impeding block isolation system has better e ff ect.The amplitude of displacement and stress is decreased with the increase of gradient factor.The e ff ect of vibration isolation of graded wave impeding block improved with the increased of the thickness,but reduced with the increasing of the embedded depths.
ground vibration control,elastic foundation,dynamic response,graded wave impeding block,reverberation ray matrix method
TU 45
A doi:10.6052/0459-1879-17-221
2017–06–12 收稿,2017–09–06 录用,2017–09–06 网络版发表.
1)国家自然科学基金资助项目(51368038).
2)周凤玺,教授,主要研究方向:岩土力学、复合材料结构力学.E-mail:geolut@163.com
马强,周凤玺,刘杰.梯度波阻板的地基振动控制研究.力学学报,2017,49(6):1360-1369
Ma Qiang,Zhou Fengxi,Liu Jie.Analysis of ground vibration control by graded wave impeding block.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1360-1369
