离散达芬映射中由边界激变所诱发的复杂的张弛振荡1)
2017-12-18陈振阳韩修静毕勤胜
陈振阳 韩修静 毕勤胜
(江苏大学土木工程与力学学院,江苏镇江212013)
离散达芬映射中由边界激变所诱发的复杂的张弛振荡1)
陈振阳 韩修静2)毕勤胜
(江苏大学土木工程与力学学院,江苏镇江212013)
多时间尺度问题具有广泛的工程与科学研究背景,慢变参数则是多时间尺度问题的典型标志之一.然而现有文献所报道的慢变参数问题,其展现出的振荡形式及内部分岔结构,大多较为单一,此外少有文献涉及到混沌激变的现象.本文以含慢变周期激励的达芬映射为例,探讨了一类具有复杂分岔结构的张弛振荡.快子系统的分岔表现为S形不动点曲线,其上、下稳定支可经由倍周期分岔通向混沌.而在一定的参数条件下,存在着导致混沌吸引子突然消失的一对临界参数值.当分岔参数达到此临界值时,混沌吸引子可能与不稳定不动点相接触,也可能与之相距一定距离.对快子系统吸引域分布的模拟,表明存在着导致边界激变(boundary crisis)的临界值,在这些值附近,经由延迟倍周期分岔演化而来的混沌吸引子可与2n(n=0,1,2,···)周期轨道乃至混沌吸引子共存.当慢变量周期地穿过临界点后,双稳态的消失导致原本处于混沌轨道的轨线对称地向此前共存的吸引子转迁,从而使系统出现了不同吸引子之间的滞后行为,由此产生了由边界激变所诱发的多种对称式张弛振荡.本文的结果丰富了对离散系统的多时间尺度动力学机理的认识.
离散达芬系统,边界激变,张弛振荡,延迟倍周期分岔
引言
许多自然现象及工程与科学研究中的问题,均涉及到不同时间尺度间的相互作用,例如厄尔尼诺与南方涛动(ENSO)现象[1]、冰川冰期的波动[2]、环境因素对农作物生长的影响[3]、激素的分泌[4]、材料在微观尺度上的力学性能[5]、声振耦合模型中的微尺度效应[6]、化工生产中液体的流动特性[7-8[9-10]、混沌吸引子的突变[11-12[13]以及Ambrosio和Azizalaoui[14]讨论了快慢耦合系统的吸引域的特性;Samoilenko等[15]通过代数推导,分析了快慢振子由阻尼振荡到多频率振荡的转迁过程.Li和Bi[16]从快慢分析的角度,对慢变周期扰动下B-Z反应中一类奇特簇发现象的产生与演化机理进行了解释.而文献[17-19]则从实验的角度,对不同模式的混沌簇放电的动力学机理进行了研究.
由于连续时间系统可通过庞加莱(Poincar´e)映射约化为离散系统,且离散系统具有数值计算上的便捷性,故而近年来,离散系统中多时间尺度效应日益受到学者们的关注.例如,基于Rinzel的快慢分析法,Izhikevich与Hoppensteadt[20]依据导致系统在沉寂态和激发态间过渡的分岔组合,系统化的探讨了一维和二维映射可能出现的簇发模式.Tanaka与Ushio[21]提出了一种用二维映射构造拥有特定周期的簇发的方法,并对相应的分岔进行了解释;Tanaka等[22]分析了一类高维映射中的分岔机理.Mo等[23]综合了实验与数值模拟的结果,对不连续映射簇发中出现的加周期(period adding)分岔现象做出了详尽的解释.Metta等[24]通过构造随机扰动下的耦合映射,讨论了离散系统中的开关间歇振荡(on-o ffintermittency)对簇发的影响机制.Shi和Lu[25]则利用二维的不连续映射,对不同耦合形式下的簇发同步现象进行了研究.
当然,需要指出的是,尽管目前关于离散系统中多时间尺度问题的研究大多是针对簇发振荡的动力学机理,但就整体而言,主要存在两方面的不足.其一,相应的振荡模式较为固定,即小幅振荡与大幅振荡的交替出现,且激发态多为周期形式的.另一方面,目前所报道的结果中,所涉及的分岔类型相对比较单一,对于由混沌激变所引发的分岔,少有文献涉及.在笔者先前的工作中[26],考虑了如下的一类二维非自治映射
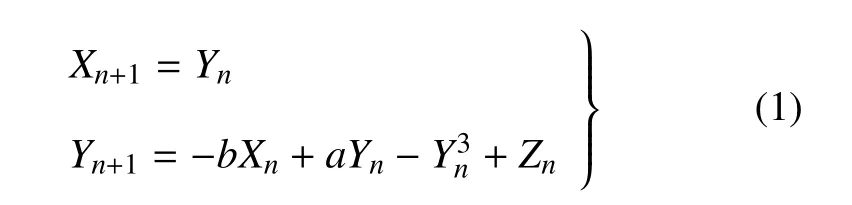
其中a,b是实参数,Zn是慢变的周期扰动.以此系统为例,我们探讨了两类具有复杂分岔结构的簇发振荡模式,即经由Fold分岔所诱发的对称式簇发,以及经由延迟倍周期分岔所诱发的非对称式簇发.在此基础之上,本文仍将对系统(1)进行分析,旨在从数值角度,探讨一类具有复杂分岔结构的对称式张弛振荡.所得的结果将表明,慢变量将诱发混沌吸引子的边界激变(boundary crisis),进而使系统发生在混沌吸引子与多种类型轨道间的对称式转迁.与此同时,由于轨线转迁到不同类型的轨道,振荡簇内部的延迟倍周期分岔也将展现出不同的几何结构,相应的延迟量与延迟次数都是不一致的,这也意味着张弛振荡的形式是丰富多样的.
1 快子系统的分岔分析
由于慢变周期扰动的存在,为了解释系统在不同参数条件下,其振荡模式的产生及演化机理,本部分将分析映射(1)所对应的快子系统

其中,β是控制参数;而慢子系统则由Zn=Fcos(ωn),ω=o(1)刻画.此外,为便于描述,本文中的a值固定为a=2.5,而外激励频率ω则取0.001.
如前文所述,本文将讨论由边界激变所诱发的复杂张弛振荡模式,并从数值角度对相关机理进行解释.所谓混沌激变,是指随着系统参数的变化,混沌吸引子突然出现或消失,或者大小与个数发生突变,文献[27-29]对混沌激变进行了详尽的分类与解释.一般来说,当混沌吸引子与其吸引域的边界相接触时,就意味着边界激变的发生,从而导致轨线逃离原来的吸引子,进而有可能发生向其它吸引子(如周期轨道)的转迁.
当轨线在不同吸引子间转迁时,往往会导致复杂的振荡模式[30].转迁形式是由快子系统的分岔行为所决定的,而慢变量穿越分岔点的方式则对耦合系统的振荡行为进行调制[31-32].因此快子系统的分岔分析对于快慢耦合系统动力学机理的解释是至关重要的,故接下来将对映射(2)的分岔行为展开讨论.
映射(2)的不动点可写成(X0,X0)的形式,其中X0由方程的实根决定.在此令b<1.5,由此可知,映射(2)可以有1至3个不动点,其临界条件是
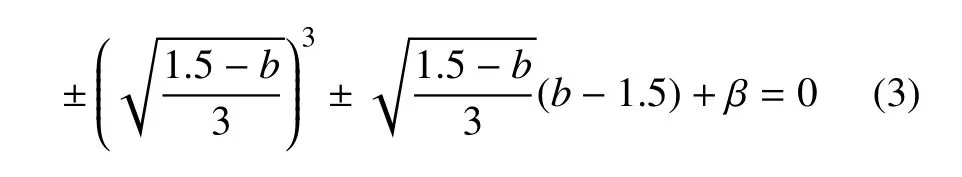
参数在临界值附近的微小扰动意味着Fold分岔的发生,即退化的不动点要么消失,要么分裂为两个不同类型的不动点.
为了进一步揭示映射(2)的分岔行为,图1以β为分岔参数,给出了当参数b取不同值时几种含混沌激变的典型分岔模式.图中用实线表示的上、下支,代表由稳定不动点F±演化出的周期轨道或混沌吸引子,而中部的虚线代表不稳定的不动点.此外,由不动点条件可知,若β=β1时,快子系统存在Fold分岔行为,那么当β=−β1时,快子系统必然也发生Fold分岔.由图1可发现,当参数b处在某些区间时,存在关于β的一对临界值对于处在临界值附近的系统,可展现由混沌吸引子与周期轨道或另一混沌吸引子构成的双稳态.而在临界值处,发生了混沌吸引子的突变,进而导致了双稳态的消失,故系统将发生向另一吸引子的转迁.因此,接下来针对几种典型的转迁模式进行讨论.

图1 快子系统关于β的单参数分岔图Fig.1 Single parameter bifurcation diagrams of the fast sub-system with respect to β

图1 快子系统关于β的单参数分岔图(续)Fig.1 Single parameter bifurcation diagrams of the fast sub-system with respect to β(continued)
情形1由混沌向周期1吸引子的转迁.选取b=0.18,可得如图1(a)所示的转迁模式.在临界点±0.175附近,系统处于混沌吸引子与周期1轨道共存的双稳态.当β越过临界值后,混沌吸引子突然消失,导致双稳态被破坏,故而系统会产生向周期1吸引子的转迁.为进一步阐明转迁的动力学机制,我们对不同转迁模式下快子系统吸引域的分布进行了数值模拟.为方便起见,在此选取β=0.174,稍小于通过给出此种参数组合下混沌吸引子与周期1吸引子的吸引域,并将两者叠加,可以发现在处,混沌吸引子与其吸引域的边界相碰.由此引发混沌吸引子的消失,导致系统进入了单稳态,故而边界激变诱发了由混沌向周期1吸引子的转迁,吸引域计算结果如图2(a)所示.
情形2由混沌向周期2吸引子的转迁.取b=0.1,快子系统可展现如图1(b)的转迁模式.由于在附近,混沌吸引子与周期2轨道共存,因此在β越过临界值后,边界激变导致了由混沌向周期2吸引子的转迁.取β=0.094,周期2轨道吸引域的计算结果如图2(b),图中实心点代表位于下半支的不稳定不动点,显然此转迁模式是由边界激变所诱发的.
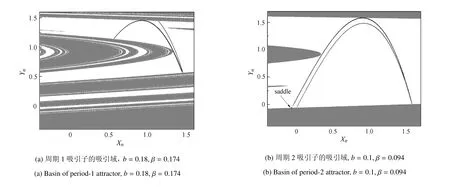
图2 位于上支的混沌吸引子与不同类型的共存吸引子的吸引域,其中白色区域表示混沌吸引子的吸引域,灰色区域为不动点或周期轨道的吸引域Fig.2 Chaotic attractor in the upper branch and basin of attraction of coexist attractor,where the white region refers to basin of chaotic attractor,while the gray region refers to basin of fi xed point or periodic orbit

图2 位于上支的混沌吸引子与不同类型的共存吸引子的吸引域,其中白色区域表示混沌吸引子的吸引域,灰色区域为不动点或周期轨道的吸引域(续)Fig.2 Chaotic attractor in the upper branch and basin of attraction of coexist attractor,where the white region refers to basin of chaotic attractor,while the gray region refers to basin of fi xed point or periodic orbit(continued)
情形3由混沌向周期4吸引子的转迁.由图1(c)可知,对b=0.062的情形,可观察到在临界值β±c附近,系统处于混沌吸引子与周期4轨道共存的双稳态.取β=0.092,通过数值计算,可得如图2(c)所示的吸引域分布.显然,当β=β±c=0.096时,发生了由边界激变导致的向周期4吸引子的转迁.
情形4由混沌向周期8吸引子的转迁.继续调整b的值,若取b=0.048,可得到如图1(d)所示的转迁行为.可以发现在β±c=±0.092附近,存在与混沌吸引子共存的周期8吸引子.取β=0.091,吸引域的分布如图2(d)所示,由此可知,边界激变将导致由混沌到周期8的转迁.
备注:由于周期1吸引子经由一系列的倍周期分岔通向混沌,进一步调整b的大小,可观察到向更高周期轨道乃至混沌吸引子的转迁模式,不失一般性,在此仅以向混沌吸引子的转迁为例.
情形5由混沌向混沌吸引子的转迁.取b=0.03,可得到如图3(a)所示的转迁模式,在β=β±c=0.09处,发生了由混沌吸引子向另一共存的混沌吸引子的转迁.令β=0.088,相应的吸引域如图3(b),显然边界激变导致双稳态的消失,这也意味着系统由混沌轨道向另一混沌轨道的转迁.
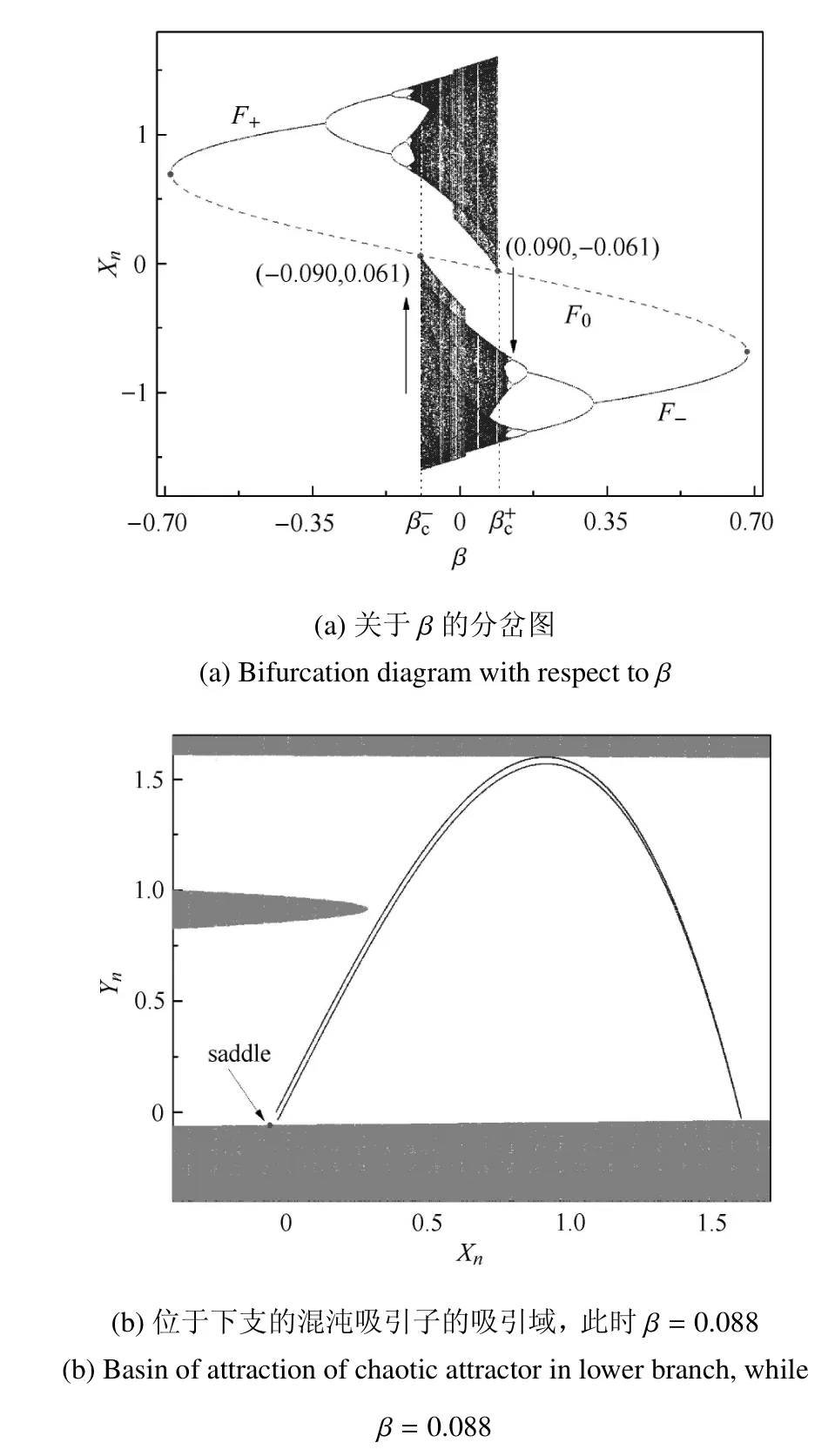
图3 由混沌向混沌的转迁模式,b=0.03Fig.3 Transition pattern of chaos to chaos,b=0.03
2 快慢耦合振荡
前一部分讨论了快子系统的分岔行为,表明了在边界激变的临界值附近,混沌吸引子可与多种周期轨道乃至混沌轨道共存,故而边界激变诱发了由混沌向不同类型的吸引子的转迁.基于此,本部分将探讨由这些转迁行为所导致的各种复杂张弛振荡模式.
2.1 “混沌--周期1”型张弛振荡
当混沌吸引子与周期1吸引子共存时,可以预见轨线将在混沌吸引子与周期1吸引子间交替转迁.不失一般性,考虑b=0.18时的分岔情形.由前面的分析可知,为使轨线实现在上、下支间的转迁,以得到不同类型的振荡行为,显然应让慢变量穿越临界值对于形如情形1的转迁模式,取慢变量振幅F=0.19,稍大于可得到如图4(a)所示的张弛振荡.为进一步阐明系统振荡行为随慢变量的变化趋势,在此将Zn视为广义变量,给出相应的转化相图[33-34].此外,为方便快慢分析的运用,将其与快子系统的单参数分岔图叠加,如图4(b)所示.
从图4(b)中可以看出,在Zn逐渐增大至的过程中,由于慢变量接连“正向”地穿过了与F+相关的多个倍周期分岔点,慢过效应(slow passage e ff ect)[7]导致了多次延迟倍周期分岔的发生,使得上半支的周期2轨道演变为混沌吸引子.当慢变量穿过临界值后,由于边界激变的出现,混沌吸引子的消失导致了双稳态被破坏,原本处于上半支的轨线会转迁到下半支的周期1吸引子,从而使系统进入平衡态.Zn在到达最大值0.19后,开始逐渐减小,并“正向”地穿过下半支吸引子各级倍周期分岔点,进而使系统由于多次延迟倍周期分岔进入到混沌形态.当Zn越过后,轨线将重复类似的过程,并进入下一个演化周期.由于系统展现出在混沌吸引子与周期1吸引子间的周期性跳跃振荡,故可将其称为“混沌--周期1”型张弛振荡.
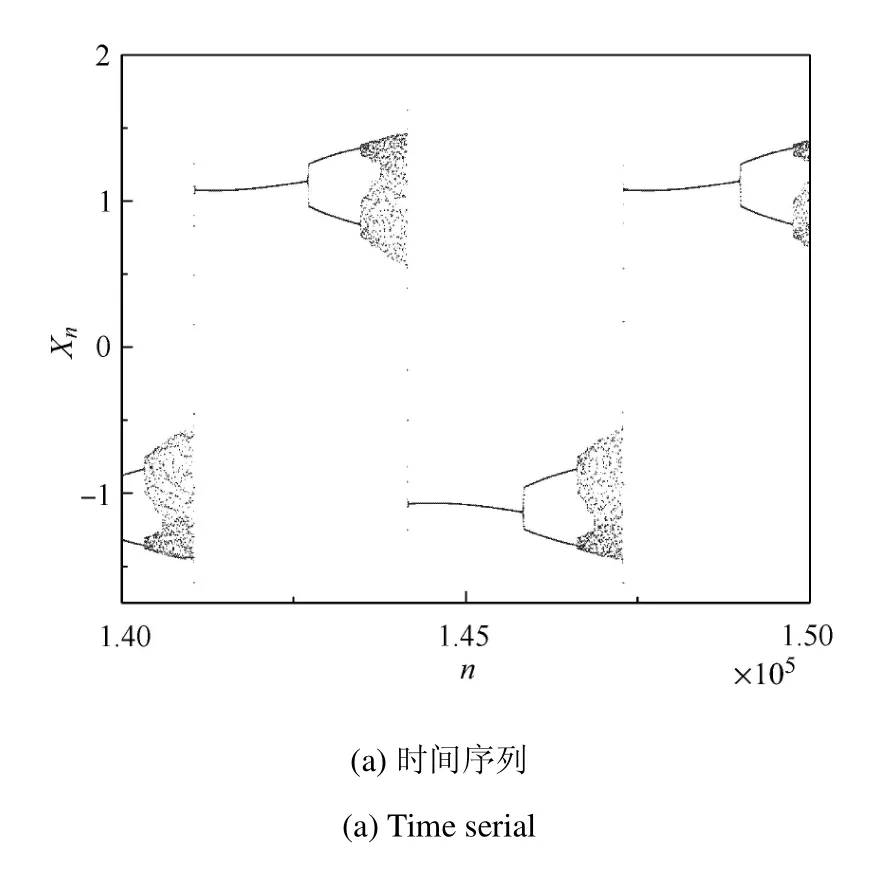

图4 “混沌--周期1”型张弛振荡,b=0.18,Zn=0.19cos(0.001n)Fig.4 “chaos-period-1”relaxation oscillation,b=0.18,Zn=0.19cos(0.001n)
2.2 “混沌--周期2”型张弛振荡
当混沌吸引子与周期2吸引子共存时,考虑如情形2的转迁形式,不难预测系统将产生另一种张弛振荡.为此可选取b=0.1,此参数条件下,若令Zn=0.11cos(ωn),可得到如图5所示的“混沌--周期2”振荡模式.由图5(b)可知,在Zn由−0.11逐渐增大的过程中,延迟效应导致原本处于周期2状态的系统经由两次延迟倍周期分岔过渡到混沌,当Zn越过后,边界激变使轨线转迁到下半支的周期2吸引子.在此之后,由于Zn接连穿过了下半支不动点曲线上的倍周期分岔点,从而导致系统的状态又由周期2逐级演变为混沌.随即系统将重复之前的演变,进入下一周期.
2.3 “混沌--周期4”型张弛振荡
对符合情形3的快子系统,若取b=0.062,并施加振幅为0.1的慢变周期激励,可得到如图6所示的“混沌--周期4”型张弛振荡.由图6(b)可知,当Zn越过后,原本处于上半支混沌吸引子的轨线会由于边界激变转迁到下半支的周期4吸引子.之后处于周期4状态的系统会由于延迟的倍周期分岔而直接转变为混沌态,进而系统将重复与之对称的过程,从而完成一个周期的演化.可将其称为“混沌--周期4”型张弛振荡.
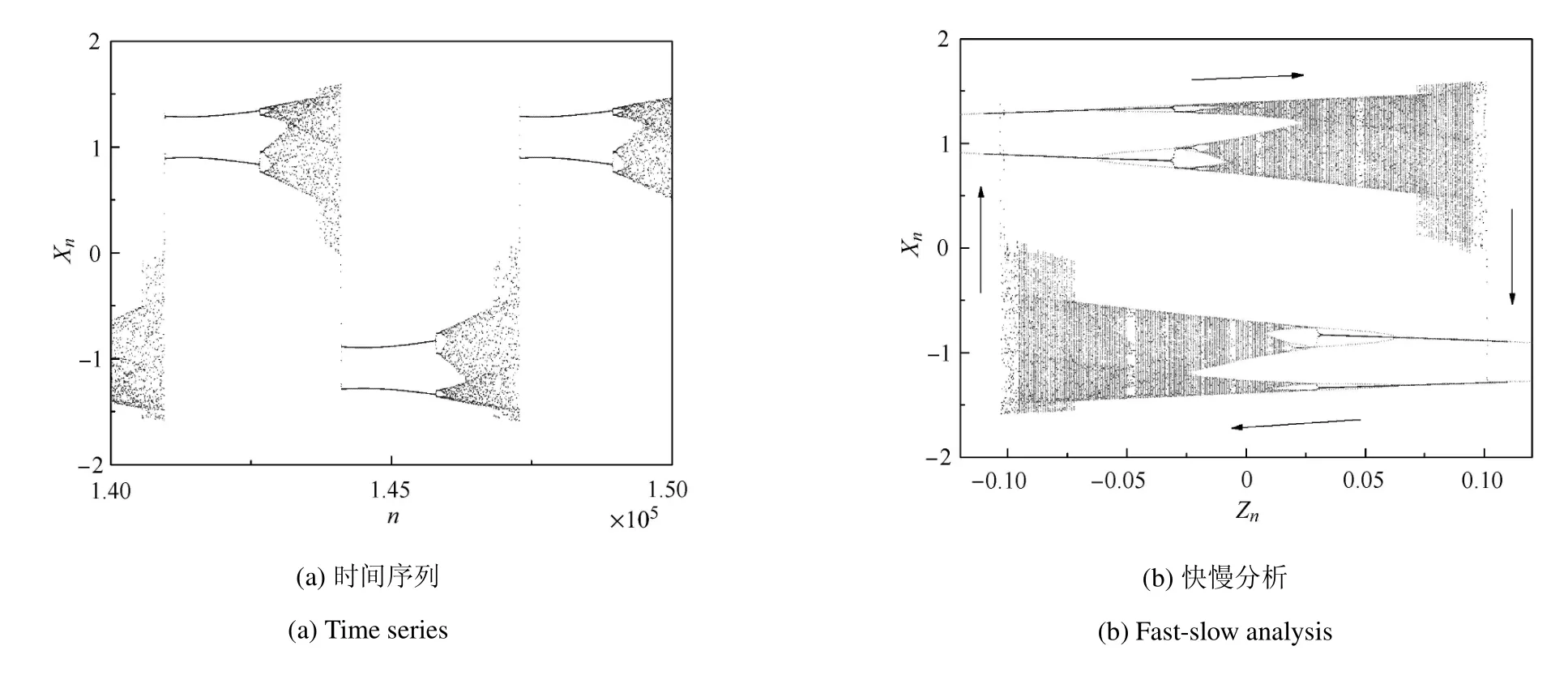
图5 “混沌--周期2”型张弛振荡,b=0.1,Zn=0.11cos(0.001n)Fig.5 “chaos-period-2”relaxation oscillation,b=0.1,Zn=0.11cos(0.001n)
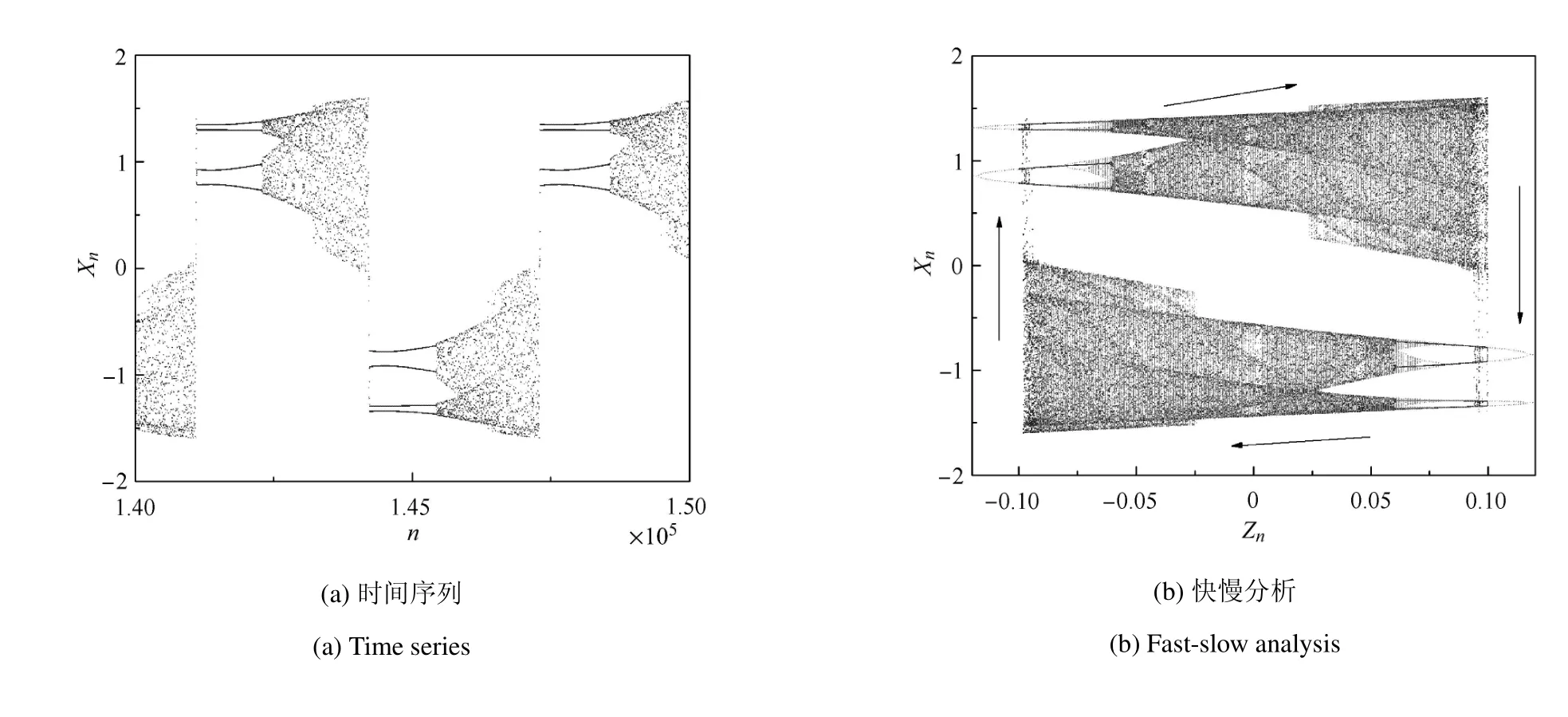
图6 “混沌--周期4”型张弛振荡,b=0.062,Zn=0.1cos(0.001n)Fig.6 “chaos-period-4”relaxation oscillation,b=0.062,Zn=0.1cos(0.001n)
2.4 “混沌--周期8”及“混沌--混沌”型张弛振荡
由快子系统的分岔行为可知,继续调整参数b的值,可得到由混沌向周期 8等更高周期轨道乃至混沌吸引子转迁的振荡模式.例如分别取b=0.048,Zn=0.1cos(ωn),以及b=0.03,Zn=0.1cos(ω·n)时,可得到另外两种由边界激变导致的张弛振荡.图 7(a)和图 7(b)展现了 “混沌--周期8”型张弛振荡,位于上半支的周期8吸引子由于延迟倍周期分岔而演变为混沌吸引子.此后随着边界激变的发生,轨线产生了由混沌向周期8轨道的转迁,显然可将其称为混沌--周期8”型振荡.进一步的,对形如情形5的转迁行为,可得到如图7(c)和图7(d)所示的“混沌--混沌”型张弛振荡.

图7 另外两种模式的张弛振荡Fig.7 Another two patterns of relaxation oscillation
3 结论
张弛振荡是多时间尺度非线性系统中典型的快慢行为.探讨张弛振荡各种可能的诱发机制并对其进行分类,是张弛振荡研究的重要问题之一.本文以两时间尺度非自治离散达芬系统为例,揭示了由边界激变所诱发的多种复杂的张弛振荡模式.研究表明,快子系统展现出具有对称结构的S形分岔曲线,其上下稳定支可经由倍周期分岔进入混沌;随后,又经由边界激变而消失.特别地,在激变点附近,可以观测到混沌与周期 2n(n=0,1,2···)轨道共存,以及混沌与混沌共存等复杂的双稳态行为.混沌吸引子的边界激变导致了双稳态行为的破坏,并诱发了系统从混沌向原先共存的各种吸引子的转迁.基于此,揭示了诸如“混沌--周期2n”型和“混沌--混沌”型等多种不同类型的张弛振荡的动力学机制.研究结果丰富了系统通向复杂的张弛振荡模式的道路.
1 Roberts A,Guckenheimer J,Widiasih E,et al.Mixed-mode oscillations of el nino-southern oscillation.J Atmos Sci,2016,73(4):1755-1766
2 Alexandrov DV,Bashkirtseva IA,Ryashko LB.Excitability,mixedmode oscillations and transition to chaos in a stochastic ice ages model.Physica D,2017,343(15):28-37
3 郭建侠,卞林根,戴永久.玉米生育期地表能量平衡的多时间尺度特征分析及不平衡原因的探索.中国科学D,2008,38(9):1103-1111(Guo Jianxia,Bian Lingen,Dai Yongjiu.Analysis of characteristics of multiple time scale in surface energy balance of corn in growth period,and exploration of the reasons for unbalance.Sci China D,2008,38(9):1103-1111(in Chinese))
4 Courbage M,Nekorkin VI,Vdovin LV.Chaotic oscillations in a map-based model of neural activity.Chaos,2007,17(4):155-160
5 卓小翔,刘辉,楚锡华等.非均质材料动力分析的广义多尺度有限元法.力学学报,2016,48(2):378-386(Zhuo Xiaoxiang,Liu Hui,Chu Xihua,et al.A generalized multiscale fi nite element method for dynamic analysis of heteroge-neous material.Chinese Journal of Theoretical and Applied Mechanics,2016,48(2):378-386(in Chinese))
6 唐宇帆,任树伟,辛锋先等.MEMS系统中微平板结构声振耦合性能研究.力学学报,2016,48(4):907-916(Tang Yufan,Ren Shuwei,Xin Fengxian,et al.Scale e ff ect analysis for the vibroacoustic performance of a micro-plate.Chinese Journal of Theoretical and Applied Mechanics,2016,48(4):907-916(in Chinese))
7 王帅,于文浩,陈巨辉等.鼓泡流化床中流动特性的多尺度数值模拟.力学学报,2016,48(3):585-592(Wang Shuai,Yu Wenhao,Chen Juhui,et al.Multi-scale simulation on hydrodynamic characteristics in bubbling fl uidized bed.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):585-592(in Chinese))
8 贾宏涛,许春晓,崔桂香.槽道湍流近壁区多尺度输运特性研究.力学学报,2007,39(2):181-187(Jia Hongtao,Xu Chunxiao,Cui Guixiang.Multi-scale energy transfer in near-wall region of turbulent channel fl ow.Chinese Journal of Theoretical and Applied Mechanics,2007,39(2):181-187(in Chinese))
9 Bear SM,Erneux T,Rinzel J.The slow passage through a Hopf bifurcation:delay,memory e ff ects,and resonance.SIAM J Appl Math,1989,49(1):55-71
10 Tzou JC,Ward MJ,Kolokolnikov T.Slowly varying control parameters,delayed bifurcations,and the stability of spikes in reactiondi ff usion systems.Physica D,2015,290(1):24-43
11 Shimizu K,Saito Y,Sekikawa M,et al.Complex mixed-mode oscillations in a Bonhoe ff er-van der Pol oscillator under weak periodic perturbation.Physica D,2012,241(18):1518-1526
12 Maslennikov OV,Nekorkin VI.Dynamic boundary crisis in the Lorenz-type map.Chaos,2013,23(2):0231291-02312916
13 Maslennikov OV,Nekorkin VI,Kurths J.Basin stability for burst synchronization in small-world networks of chaotic slow-fast oscillators.Phys Rev E,2015,92(4):04280311-042803110
14 Ambrosio B,Azizalaoui MA.Basin of attraction of solutions with pattern formation in slow-fast reaction-di ff usion systems.Acta Biotheor,2016,64(4):311-325
15 Samoilenko AM,Parasyuk IO,Repeta BV.Dynamical bifurcation of multifrequency oscillations in a fast-slow system.Ukr Math J,2015,67(7):1008-1037
16 Li XH,Bi QS.Single-hopf bursting in periodic perturbed belousovzhabotinsky reaction with two time scales.Chinese Phys Lett,2013,30(1):10503-10506
17 古华光,朱洲,贾冰.一类新的混沌神经放电的动力学特征的实验和数学模型研究.物理学报,2011,60(10):1005051-10050512(Gu Huaguang,Zhu Zhou,Jia Bing.Dynamics of a novel chaotic neural fi ring pattern discovered in experiment and simulated in mathematical model.Acta Phys Sin,2011,60(10):1005051-10050512(in Chinese))
18 古华光,惠磊,贾冰.一类位于加周期分岔中的貌似混沌的随机神经放电规律的识别.物理学报,2012,61(8):0805041-08050410(Gu Huaguang,Hui Lei,Jia Bing.Identi fi cation of a stochastic neural fi ring rhythm lying in period-adding bifurcation and resembling chaos.ActaPhysSin,2012,61(8):0805041-08050410(inChinese))
19 Gu HG.Experimental observation of transition from chaotic bursting to chaotic spiking in a neural pacemaker.Chaos,2013,23(2):023126-1-9
20 Izhikevich EM,Hoppensteadt F.Class fi cation of bursting mapping.Int J Bifurcat Chaos,2004,14(11):3847-3854
21 Tanaka H,Ushio T.Design of bursting in a two-dimensional discrete-time neuron model.Phys Lett A,2004,350(3):228-231
22 Tanaka H,Ushio T,Kawanami S.A high-dimensional chaotic discrete-time neuron model and bursting phenomena.Phys Lett A,2003,308(1):41-46
23 Mo J,Li YY,Wei CL,et al.Interpreting a period-adding bifurcation scenario in neural bursting patterns using border-collision bifurcation in a discontinuous map of a slow control variable.Chinese Phys B,2010,19(8):225-240
24 Metta S,Provenzale A,Spiegel EA.On–o ffintermittency and coherent bursting in stochastically-driven coupled maps.Chaos Soliton Fract,2010,43(1-12):8-14
25 Shi X,Lu QS.Burst synchronization of electrically and chemically coupled map-based neurons.Physica A,2009,388(12):2410-2419
26 陈振阳,韩修静,毕勤胜.一类二维非自治离散系统中的复杂簇发振荡结构.力学学报,2017,49(1):165-174(Chen Zhenyang,Han Xiujing,Bi Qinsheng.Complex bursting structures in a twodimensional non-autonomous discrete system.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1):165-174(in Chinese))
27 Grebogi C,Ott E,Yorke JA.Chaos,strange attractor,and fractal basin boundaries in nonlinear dynamics.Science,1987,238(4827):632-638
28 Grebogi C,Ott E,Yorke JA.Crisis,sudden change in chaotic attractor and transient chaos.Physica D,1983,7(1-3):181-200
29 Arnold VI,Afraimovich VS,Ilyashenko Yu S,et al.Dynamical Systems V:Bifurcation Theory and Catastrophe Theory.New York:Springer,1993:145-150
30 陈章耀,陈亚光,毕勤胜.由多平衡态快子系统所诱发的簇发振荡及机理.力学学报,2015,4(4):699-706(Chen Zhangyao,Chen Yaguang,Bi Qinsheng.Bursting oscillation as well as the bifurcation mechanism induced by fast subsystem with multiple balances.Chinese Journal of Theoretical and Applied Mechanics,2015,4(4):699-706(in Chinese))
31 Kuehn C.Multiple Time Scale Dynamics.New York:Springer,2015:8-14
32 Wu HG,Bao BC,Liu Z,et al.Chaotic and period bursting phenomena in a memristive Wien-bridge oscillator.Nonlinear Dyn,2016,83(1-2):893-903
33 Han XJ,Bi QS.Bursting oscillations in Duffing’s equation with slowly changing external forcing.Commun Nonlinear Sci Numer Simul,2011,16(10):4146-4152
34 张晓芳,陈小可,毕勤胜.快慢耦合振子的张驰簇发及其非光滑分岔机制.力学学报,2012,44(3):576-583(Zhang Xiaofang,Chen Xiaoke,Bi Qinsheng.Relaxation bursting of a fast-slow coupled oscillation as well as the mechanism of non-smooth bifurcation.Chinese Journal of Theoretical and Applied Mechanics,2012,44(3):576-583(in Chinese))
COMPLEX RELAXATION OSCILLATION TRIGGERED BY BOUNDARY CRISIS IN THE DISCRETE DUFFING MAP1)
Chen Zhenyang Han Xiujing2)Bi Qinsheng
(Faculty of Civil Engineering and Mechanics,Jiangsu University,Zhenjiang212013,Jiangsu,China)
Multiple-time scale problems are ubiquitous in both science and engineering,while the slow varying parameter is one of the iconic feature of multiple-time scale.However,up till now,most of bifurcation structures and oscillation patterns revealed by literatures are relatively simplex.In this paper,we take the non-autonomous Duffing map as a example to explore family of complex relaxation oscillation patterns,which are little concerned by previous study.The fast subsystem exhibits an S-shaped fi xed point curve,and the stable upper and lower branches evolve into chaos by a cascade of Flip bifurcations.What’s more,we can observe a pair of critical parameter values under some parameter conditions,which lead to the catastrophe vanish of chaotic attractors.When the bifurcation parameter reaches these values,chaotic attractors may contact with the unstable fi xed point or just stay in a distance apart.By simulating the distribution of basins of attraction owned by fast subsystem,we show that there exist critical points of boundary crisis,nearby which chaotic attractor evolved from stable fi xed points can coexist with period-2n(n=0,1,2,···)attractor or even another chaotic attractor.When the non-autonomous term(i.e.,the slow variable)passes through critical points,distruction of bi-stability may lead to the transition from chaotic attractor in pre-crisis stage to the coexisting attractor,thus the boundary crisis motivates di ff erent patterns of symmetric relaxation oscillation.In particular,patterns here show structures containing di ff erent number of delay fl ip bifurcations,owe to the fact that delay quantities of Flip points in di ff erent level take disparate magnitude.Our results enrich dynamical mechanisms of multiple-time scale in discrete systems.
discrete Duffing system,boundary crisis,relaxation oscillation,delayed fl ip bifurcations
O322
A doi:10.6052/0459-1879-17-138
2017–04–24 收稿,2017–06–26 录用,2017–06–26 网络版发表.
1)国家自然科学基金(11572141,11632008,11502091,11472115,11402226)和江苏大学青年骨干教师培养工程资助项目.
2)韩修静,副教授,主要研究方向:动力学与控制.E-mail:xjhan@mail.ujs.edu.cn
陈振阳,韩修静,毕勤胜.离散达芬映射中由边界激变所诱发的复杂的张弛振荡.力学学报,2017,49(6):1380-1389
Chen Zhenyang,Han Xiujing,Bi Qinsheng.Complex relaxation oscillation triggered by boundary crisis in the discrete Duffing map.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1380-1389
