可降解聚合物血管支架结构优化设计1)
2017-12-18赵丹阳李红霞王敏杰
赵丹阳 刘 韬 李红霞,†,2) 王敏杰
*(大连理工大学机械工程学院,大连116023)
†(郑州大学微纳成型技术国家级国际联合研究中心及河南省微成型重点实验室,郑州450001)
可降解聚合物血管支架结构优化设计1)
赵丹阳*刘 韬*李红霞*,†,2)王敏杰*
*(大连理工大学机械工程学院,大连116023)
†(郑州大学微纳成型技术国家级国际联合研究中心及河南省微成型重点实验室,郑州450001)
聚合物血管支架由于材料刚度较低导致其径向支撑能力相对于金属血管支架较弱,通常采用增大支架筋宽和厚度的方式来提高其径向支撑能力,但这不仅会降低支架的柔顺性能,减小血管管腔获得面积,还会增大表面覆盖率,从而增大支架内再狭窄的风险.为了设计出具有较小筋宽和厚度的聚合物血管支架,提高其径向支撑能力,本文采用一种将Kriging代理模型和有限元方法相结合的优化方法来优化支架的结构.采用Kriging代理模型建立设计目标和设计变量之间近似的函数关系,采用优化拉丁超立方抽样方法选取初始样本点,采用EI函数平衡局部和全局搜索,以便获得全局最优解.选取ART18Z聚合物支架作为算例,首先将支架的筋宽和厚度各减小0.02mm,然后采用优化方法优化ART18Z支架的几何结构参数.数值结果表明,优化后ART18Z支架的综合服役性能得到改善,文中提出的优化方法能有效地应用于聚合物血管支架的优化设计.
可降解聚合物,血管支架,力学性能,Kriging代理模型,优化设计
引言
随着微创介入治疗技术的发展,血管支架植入术已经发展成为治疗心血管狭窄率疾病最有效的方法之一.可降解聚合物血管支架是血管支架的重要发展方向,它避免了永久性金属支架作为永久异物所导致的炎症反应、平滑肌增生和迁移、内膜增生以及细胞外基质的聚集等病变引起的支架内再狭窄和远期安全性问题[1-8].然而,聚合物血管支架由于聚合物材料本身的弹性模量较低导致支架径向支撑能力相对于金属血管支架较弱,在球囊扩张并卸载后支架产生较大的径向弹性回缩,减小了支架内管腔获得面积和血管内血流通过量,并影响血管管腔重塑[9].目前,通常采用增大支架筋宽和厚度的方式来提高聚合物支架的径向支撑能力,如Ideal支架的厚度是0.2mm,Igaki-Tamai支架和ART18Z支架的厚度均为0.17mm,BVS支架和DeSolve支架的厚度都是0.15mm[10-11].然而,增大支架的筋宽和厚度不仅会降低支架的柔顺性能,减小血管管腔获得面积,而且较大的表面覆盖率还会增大新生内膜增生几率,从而增大支架内再狭窄的风险.所幸的是,支架的结构也会对支架的力学性能产生影响,可以通过改进支架的结构设计来改善支架的力学性能.
目前,血管支架结构设计的研究主要依赖于实验和临床,存在许多的困难和局限性,不仅费时,难度大而且成本较高,同时,某些重要参数,如支架结构内部的应力和应变分布等也较难通过实验获取.随着计算机科学技术的发展,数值计算技术模拟分析血管支架行为的研究解决了仅依靠实验存在的困难和局限,近年来被广泛采用.目前基于数值计算的支架结构设计主要是结构参数的对比分析,即对比分析几款不同结构的支架设计,或同款结构几组不同尺寸参数支架设计的力学性能,从中选取力学性能“最好”的一个设计作为支架的“最佳”设计[12-21].这种方法易于研究影响支架设计的因素,但只能在有限个设计中选取“最佳”设计,不能在设计区间内找出全局最优设计.并且,支架的有限元计算涉及到大变形和弹塑形共存等非线性问题,单个计算量较大,而要找到较好的支架设计,需要做大量的对比分析,其计算量将十分巨大.
与对比分析法相比,代理模型的方法能建立设计变量和设计目标之间难以显性表达的近似函数关系,将复杂的工程问题转化为可求解的数学问题,大大降低计算成本.将数值计算与代理模型相结合的优化算法能更简便快捷地对支架进行优化.Atherton和Bate[22]用代理模型的方法研究了支架对血管的壁面剪切应力的影响,优化了支架结构.Harewood等[23]用代理模型研究了支架一个单环的径向刚度.Clune等[24]利用响应面技术优化了支架的抗疲劳特性.在众多代理模型技术中,Kriging代理模型在对未知信息的模拟精度上具有明显的优势,并且其计算模型更加简洁,能够更加方便地应用于工程问题的研究.Kriging代理模型包含参数模型和非参数随机过程两个因素,因此,比仅具有参数模型的插值方法[25-26]在具体应用中更加灵活,比非参数化模型具有更强的全局预测能力.Li等[27-28]利用基于Kriging代理模型的自适应优化算法分别优化了支架结构和支架涂层,消除了支架扩张过程中的狗骨头效应,延长了药物释放的有效时间.李红霞等[29]采用与有限元技术相结合的Kriging代理模型对基于不同扩张模拟方式的支架进行了优化.Pant等[30]采用Kriging代理模型优化了支架力学性能、药物释放效果和柔顺性能.Srinivas等[31]对简化的支架二维稳态流动模型进行了优化.利用代理模型技术,使得血管支架更为复杂和细致的研究成为可能.
综上所述,针对目前可降解聚合物血管支架普遍存在的径向支撑能力较弱的问题,为了设计出具有较小筋宽和厚度,同时具有较好支撑性能的聚合物血管支架,本文以ART18Z聚合物支架为研究对象,先将其筋宽和厚度各减小 0.02mm,即支架的筋宽减小15.38%,厚度减小13.33%,然后采用改进的Kriging代理模型的优化方法,以减小支架扩张后的径向弹性回缩为设计目标,对其结构进行优化设计,以达到改善ART18Z聚合物支架服役性能的目的.
1 有限元模拟
以长 13.75mm,厚 0.17mm,外直径 3.36mm的ART18Z支架为研究对象.带有直桥连接单元的ART18Z聚合物支架的三维模型如图1所示.

图1 带有直桥连接单元的ART18Z聚合物支架Fig.1 ART18Z polymeric stent with straight bridge connection unit
采用血管、血栓、支架和球囊的三维分析模型进行有限元分析,利用ANSYS软件包分析聚合物支架在狭窄血管内的扩张过程,其三维有限元模型如图2所示.由于整个模型具有对称性,故在此研究中选取了整个模型的1/12(周向1/6、轴向1/2)进行模拟计算.在支架扩张过程计算的有限元模型中,血管长7.9mm,厚度保持一致,均为0.15mm;血栓斑块近端的厚度为0.48mm,远端的厚度为0.08mm,在扩张开始的时候血栓斑块并没有与支架接触;球囊长7.75mm,厚0.05mm.

图2 狭窄动脉血管内聚合物支架扩张的有限元模型Fig.2 Finite element model of polymeric stent expansion in stenotic artery
1.1 材料属性
PLLA具有良好的生物相容性和可控的降解速率,在可降解聚合物血管支架的制备上具有广阔的应用前景.ART18Z支架材料为PLLA,其弹性模量为3363MPa,泊松比0.45,屈服强度40MPa,等效为双线性、各向同性弹塑性材料.血管和血栓弹性模量分别为1.75MPa和2.19MPa,泊松比均为0.499,等效为线性、各向同性的近似不可压缩材料.球囊的弹性模量参数为C10=1.0688MPa,C01=0.710918MPa,泊松比0.495,等效为超弹性橡胶材料.在进行有限元分析中,血管、血栓和支架均采用8节点Solid 185实体单元,球囊则采用4节点Shell 181壳单元.模拟过程中的材料性能参数来源于文献[32].材料属性如表1所示.

表1 材料属性Table 1 Material properties
1.2 载荷与边界条件
支架扩张是一个非线性大变形过程,本文采用具有较高计算精度的六面体网格划分模型.考虑球囊和支架的接触,以及支架和血栓的接触.为模拟支架在球囊膨胀作用下扩张和球囊卸载后支架的变形过程,在球囊上施加两步径向位移载荷:第一步,将支架的外直径扩张到血管的内部直径;第二步,将球囊卸载到最初的状态.血管、血栓、支架和球囊的对称部分施加对称约束,球囊远端约束轴向刚体位移,血管、血栓和支架的远端自由.
1.3 有限元分析结果
在扩张过程中,支架在球囊膨胀的作用下逐渐被扩张,将狭窄血管撑开.当球囊卸载后,支架由于塑性变形仍然处于扩张状态,从而支撑狭窄血管.图3描述的是聚合物支架在狭窄血管内的膨胀过程,其中(a)∼(c)指的是支架从原始状态逐渐扩张到最大程度的过程,(d)∼(e)描述的是球囊卸载后的过程.
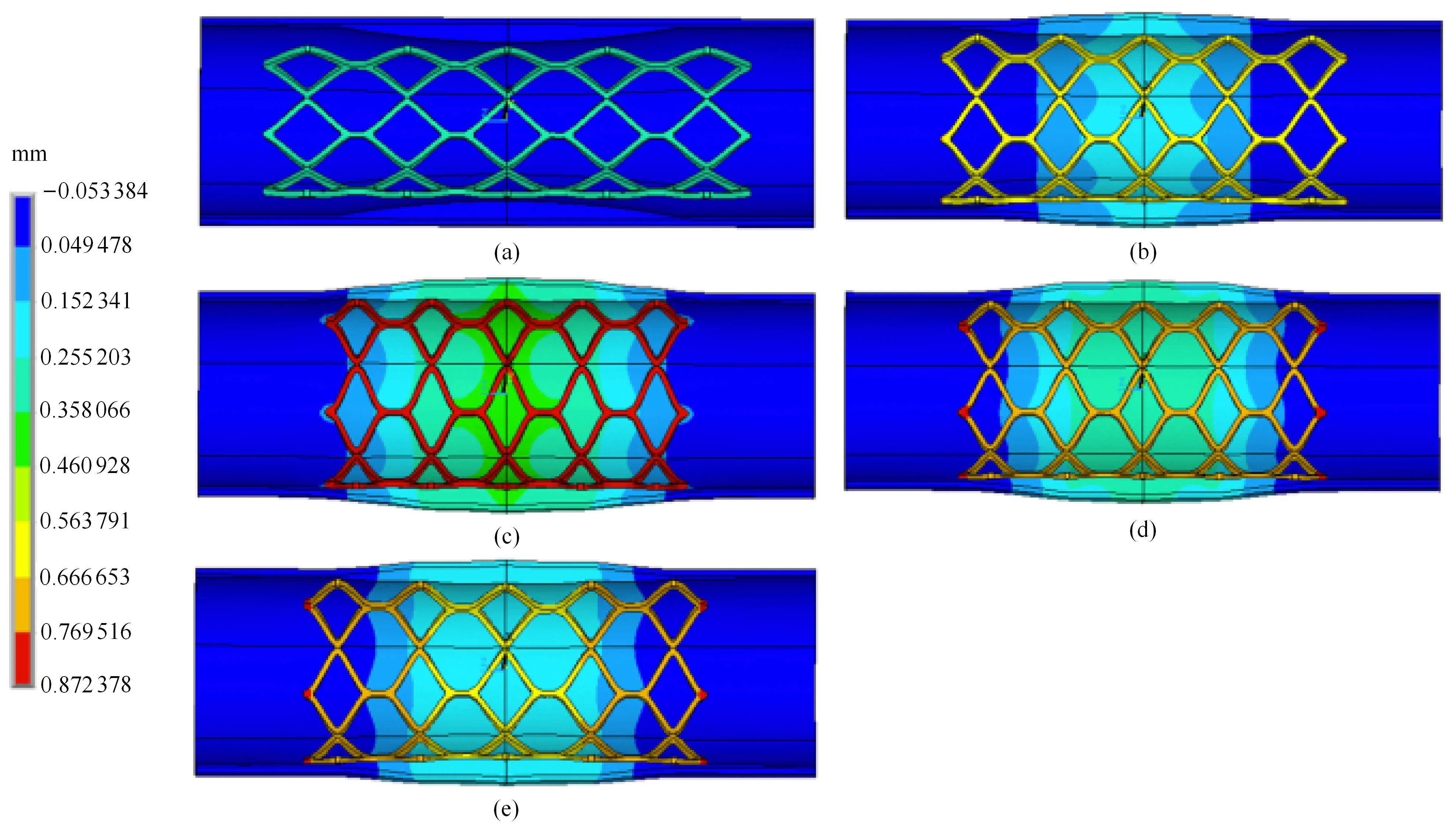
图3 聚合物支架在狭窄血管内的膨胀过程(a)∼(c):膨胀过程,(d)∼(e):球囊卸载过程Fig.3 The expansion process of polymeric stent in stenotic artery(a)∼(c):The expansion process,(d)∼(e):The de fl ation of the balloon
2 优化设计
2.1 优化问题
径向回缩率(radial recoil,RR)是血管支架扩张性能的重要技术指标.由于PLLA材料刚度较低,导致PLLA支架的径向支撑能力较弱,支架在球囊卸载之后会出现较大的径向弹性回缩,这将减小血管内血流通过量,并影响血管管腔重塑.此外,支架的覆盖面积较大还会造成血管壁的内膜增生,因此通常将其限制在20%以下.本文先将支架的筋宽和厚度各减小0.02mm,然后以支架的关键结构尺寸为设计变量,以支架扩张后的径向弹性回缩为设计目标对支架进行优化设计,优化问题可定义为
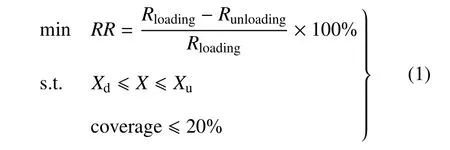
式中,Rloading是支架完全扩张时的半径,Runloading是卸载后支架的半径,X是支架的设计变量,包含支架的几何参数a和b,如图1所示,图中a和b分别是菱形孔的长和宽;Xu和Xd分别是设计变量的上下限,且2.2mm6a62.6mm,1.4mm6b61.6mm.
2.2 优化算法
在工程优化设计中,采用代理模型建立设计变量与设计目标之间难以显性表达的函数关系,可将复杂工程问题转化为可求解的数学问题,大大降低计算成本.
采用基于改进的Kriging代理模型的优化算法对血管支架进行优化设计过程的流程如图4所示,其主要过程为:
(a)定义优化问题,即定义设计变量、设计目标和约束条件;
(b)通过优化拉丁超立方取样方法获取初始样本点,并通过有限元分析计算每个设计样本点,得出每个样本点的响应值(即径向回缩率);
(c)基于样本点信息,Kriging代理模型采用二次多项式响应面形式来构建设计目标和设计变量之间近似的函数关系;
(d)选择样本点中响应值最小的点作为优化程序执行的初始点,并选择优化算法来获得基于近似函数关系的最优设计;
(e)检查收敛条件,当满足收敛条件时,优化程序停止.

图4 基于代理模型的优化算法过程的流程图Fig.4 Flow chart of the process of optimization algorithm based on surrogate model
(1)Kriging代理模型
Kriging代理模型是一种具有“统计性”的近似技术,包括回归部分和非参数部分,由多项式和随机分布组成

式中,β为回归系数,f(x)为x的多项式,提供模拟的全局近似;z(x)为随机分布的误差,提供对模拟局部偏差的近似,具有如下统计特性

式中,xi和xj是训练样本中的任意两个点,R(θ,xi,xj)是带有参数θ的相关函数,表征训练样本点之间的空间相关性.这里采用高斯相关函数
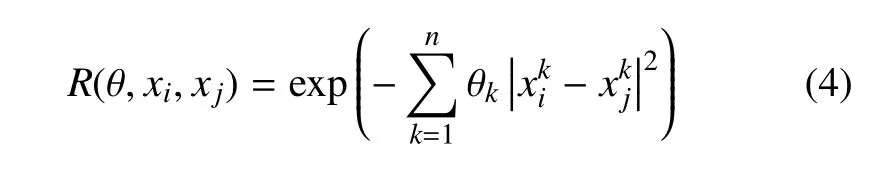
式中,n为设计变量的数量,和为训练样本点的第k个分量.
给定训练样本S=[x1,x2,···,xni]和对应的响应Y=[y1,y2,···,yns],在式 (2)假定的基础上,任意一个待测点x*的响应值可由已知训练样本响应值Y的线性组合来表达

则误差为

把式(2)代入式(6)得

式中,F=[f1,f2,···,fns],Z=[z1,z2,···,zns].为保证模拟过程的无偏性,误差的均值应该为0,即

可得,FTc−f=0.则式(7)的预测方差为

式中

代表新样本点x*和各样本点的空间相关性.通过最小化预测值的预测方差来确定方差系数c,可以得到

至此,可以根据式(12)得到任意新点x*处的预测值
(2)取样方法
采用优化拉丁超立方抽样方法取样,该方法由拉丁超立方抽样方法改进而来的.拉丁超立方取样的主要优点是确保选出的样本点可以代表样本空间中的所有部分,其次是这种取样方式获取的样本点数目不受变量维数限制,可以是任意整数,使用起来方便.但因为拉丁超立方取样具有随机性,会使得获取的样本点时好时差,因此,本文采用的是由Joseph等[33]提出的改进的拉丁超立方取样,即优化拉丁超立方取样.它是在拉丁超立方取样的基础上,以最小化样本点中点与点之间的两两相关性,并同时最大化点与点之间的距离为标准,对样本点的空间分布重新进行优化.图5为拉丁超立方取样及优化拉丁超立方取样图,通过比较可以看出优化拉丁超立方取样产生的样本点效果更好.

图5 拉丁超立方取样和优化拉丁超立方取样Fig.5 Latin hypercube sampling and optimized Latin hypercube sampling
(3)EI函数
最大化期望提高是考虑预测值和预测方差加权的一种加点方法.期望提高(expected improvement,EI)是指计算在一个给定点的响应值目标提高的概率.对于任意一个设计点x,在计算其响应值y(x)之前,y(x)是未知的,但kriging能够预测它的均值和均方差σ2(x).假设当前最优设计的响应值为Ymin,则该点的响应值目标的提高I(x)=Ymin−y(x),它服从正态分布,则其概率密度函数为

那么响应值目标提高的期望值为

分部积分可得

式中,Φ和ϕ分别为正则化概率分布函数和概率密度函数.
(4)收敛条件

式中,Ymax和Ymin分别是样本点中最大和最小的响应值,fk和fk−1分别是通过ANSYS计算得到的第k步和k−1步的响应值,表示Kriging在第k步的预测值,ε1,ε2和ε3分别为给定的收敛精度.
由于可降解聚合物血管支架优化设计中存在模型复杂、计算量大和高度的非线性等问题,本文采用改进的Kriging代理模型优化设计方法对ART18Z支架的关键几何尺寸进行优化设计.在该优化算法中,采用Kriging代理模型建立设计变量和设计目标之间近似的函数关系,运用优化拉丁超立方抽样方法获取最初样本点,并利用期望提高(EI)函数平衡局部和全局搜索,防止得到局部最优解.
2.3 优化结果与讨论
以支架的菱形孔的长和宽为设计变量,采用优化拉丁超立方抽样方法在设计空间内选取30个初始样本点,经过21步迭代后得到最优结果.
表2对比了优化支架、原始设计支架和参照支架(在支架原始设计的基础上,仅将筋宽和厚度减小0.02mm,其他条件不变)的结果.与原始设计支架相比,优化支架与原始设计支架的径向回缩率差别很小,这说明即使优化支架的筋宽减小了15.38%,厚度减小了13.33%,但优化支架具有与原始设计支架相近的径向支撑能力;且优化支架筋宽和厚度较小,使得优化支架柔顺性优于原始支架,更利于支架在血管中的输送.此外,优化支架的表面覆盖率比原始设计支架的小,从而减小了新生内膜增生几率,降低了支架内再狭窄的风险;优化支架的血管管腔获得面积也比原始支架的大,血流流经血管更加通畅,有利于保证支架内血流通过量.总的来说,优化支架在明显减小筋宽和厚度的前提下,具有与原始设计支架相近的径向支撑能力,提高了支架的柔顺性,增大了血管管腔获得面积,降低了支架表面覆盖率,从而改善了支架的综合服役性能.

表2 支架结构优化后与原始设计支架和参考支架的对比Table 2 Optimization result of stent structure compared to the original stent and comparable stent
与单纯减小支架筋宽和厚度的参照支架相比,尽管优化支架与其有相同的宽度和厚度,但是优化支架的径向回缩率比参照支架的小2.58%,这表明优化支架具有更好的径向支撑能力,而优化支架的血管管腔获得面积也比参照支架的大6.21%,更利于保证支架内血流通过量,且优化支架表面覆盖率与参照支架很相近.
综上所述,虽然减小支架的筋宽和厚度有利于降低血管支架的表面覆盖率、增大管腔面积并提高支架的柔顺性,但单纯减小支架的筋宽和厚度,必然会降低支架的力学性能,尤其是径向支撑能力.然而,在减小支架筋宽和厚度的前提下,通过对支架结构进行优化设计,提高支架的力学性能,使其与筋宽和厚度较大的支架具有相似的力学特性,同时还能增大管腔面积,减小覆盖率,提高其综合服役性能,从而有利于降低再狭窄的风险.
图6显示的是其他三个设计变量为最优值时,每个设计变量对径向弹性回缩的影响.支架的径向弹性回缩率随着支架筋宽和厚度的增大而减小,这是因为随着支架宽度和厚度的增大,支架的径向刚度也随之增大,从而使得支架的径向弹性回缩率减小.菱形孔的长度在设计范围内有一个最优值使得支架的径向弹性回缩最小,而菱形孔的宽度在设计范围有一个值使得支架的径向弹性回缩最大.这是因为研究的支架结构中,既有菱形也有六边形,而且他们共边.菱形的结构影响了六边形的几何结构,从而对支架的径向弹性回缩产生了影响.此外,支架的径向弹性回缩不仅与支架结构相关,而且与聚合物支架的材料和膨胀过程相关.
3 结论
本文针对可降解聚合物血管支架存在的径向刚度较弱,以及血管支架优化设计中存在的多重非线性耦合,传统的梯度类优化算法易落于局部最优,智能算法存在超大规模计算量的问题,提出了可降解聚合物血管支架的代理模型优化设计方法.并选取典型的ART18Z支架作为算例对其进行结构尺寸优化设计.经过优化后改善了该支架的综合服役性能.数值结果表明:该优化设计方法能有效地应用于可降解聚合物血管支架的结构优化设计.

图6 单个变量对径向弹性回缩的影响Fig.6 The in fl uence of individual variable on radial elastic recoil
Kriging代理模型的优化算法具有较好的精确度和稳健性,对于多学科优化问题,尤其是对于解决支架优化这类模型复杂、计算量大、高度的非线性的问题具有很大优势.除了本文所提出的优化支架径向回缩的问题,此优化算法还能解决其他支架优化的问题,如改善支架的扩张性能、提高支架服役期的疲劳寿命、降低支架轴向缩短率等.Kriging代理模型的优化算法能有效地运用于血管支架的优化设计,建立设计目标和设计变量之间的近似函数关系,代替优化过程中费时的有限元计算,解决了冠脉支架设计中的设计目标与设计变量之间关系复杂且不能显式表达的问题,为血管支架的优化设计提供新的思路和方法.
作为可降解聚合物血管支架优化设计的阶段性研究,本文在优化设计的目标函数中仅将径向弹性回缩作为设计目标,而将覆盖率作为约束来考虑,在后期工作中可在目标函数中适当考虑多个设计目标;此外,在优化过程中,对样本点的计算需要耗费大量计算量,在后期工作中可考虑血管支架优化设计的并行算法,以提高优化效率.
1 Rivard A,Andr´es V.Vascular smooth muscle cell proliferation in the pathogenesis of atherosclerotic cardiovascular diseases.Histology and Histopathology,2000,15(2):557-571
2 葛均波.支架内再狭窄 2014:当前问题.医心评论,2014(Ge Junbo.Intraventricular restenosis 2014:Current problem.Medical Heart Review,2014(in Chinese))
3 葛均波,葛雷,黄榕翀.慢性完全闭塞病变介入治疗进展与展望.心血管病学进展,2007,28(2):165-167(Ge Junbo,Ge Lei,Huang Rongzhong.Advances in interventional therapy of chronic total occlusion.Advances in Cardiovascular Diseases,2007,28(2):165-167(in Chinese))
4 高润霖.药物洗脱支架研究现状及进展.中国实用内科杂志,2006,26(15):1121-1123(Gao Runlin.Research status and development of drug-eluting stents.Chinese Journal of Practical Internal Medicine,2006,26(15):1121-1123(in Chinese))
5 易勇,陈玉成,曾智.冠脉支架内再狭窄防治研究进展.心脏杂志,2003,15(6):560-562(YiYong,ChenYucheng,ZengZhi.Advances in prevention and treatment of coronary stent restenosis.Heart Magazine,2003,15(6):560-562(in Chinese))
6 Sousa JE,Serruys PW,Costa MA.New frontiers in cardiology drugeluting stents:Part I.Circulation,2003,107(17):2274-2279
7 Jr DJ.Role of adjunct pharmacologic therapy in the era of drugeluting stents.Atherosclerosis Supplements,2005,6(4):47-52
8 刘赵淼,南斯琦,史艺.中等严重程度冠状动脉病变模型的血流动力学参数分析.力学学报,2015,47(6):1058-1064(Liu Zhaomiao,Nan Siqi,Shi Yi.Hemodynamic parameters analysis for coronary artery stenosis of intermediate severity model.Chinese Journal of Theoretical and Applied Mechanics,2015,47(6):1058-1064(in Chinese))
9 Bresslo ffNW.Multi-Objective Design of a Biodegradable Coronary Artery Stent.Cardiovascular and Cardiac Therapeutic Devices:Springer Berlin Heidelberg,2013:1-28
10 Zhang YJ,Bourantas CV,Farooq V,et al.Bioresorbable sca ff olds in the treatment of coronary artery disease.Medical Devices Evidence&Research,2013,6(1):37-48
11 Kraak RP,Grundeken MJ,Koch KT,et al.Bioresorbable sca ff olds for the treatment of coronary artery disease:Current status and future perspective.Expert Review of Medical Devices,2014,11(5):467-480
12 Pauck RG,Reddy BD.Computational analysis of the radial mechanical performance of PLLA coronary artery stents.Medical Engineering&Physics,2014,37(1):7-12
13 Rogers C,Tseng DY,Squire JC,et al.Balloon-artery interactions during stent placement:A fi nite element analysis approach to pressure,compliance,and stent design as contributors to vascular injury.Circulation Research,1999,84(4):378-383
14 Etave F,Finet G,Boivin M,et al.Mechanical properties of coronary stents determined by using fi nite element analysis.Journal of Biomechanics,2001,34(8):1065-1075
15 Migliavacca F,Petrini L,Colombo M,et al.Mechanical behavior of coronary stents investigated through the fi nite element method.Journal of Biomechanics,2002,35(6):803-811
16 Mori K,Saito T.E ff ects of stent structure on stent fl exibility measurements.Annals of Biomedical Engineering,2005,33(6):733-742.
17 Wu W,Yang DZ,Huang YY,et al.Topology optimization of a novel stentplatformwithdrugreservoirs.MedicalEngineering&Physics,2008,30(9):1177-1185
18 DeBM,VanIR,VerheggheB,etal.Finiteelementanalysisandstent design:Reduction of dogboning.Technology&Health Care Official Journal of the European Society for Engineering&Medicine,2006,14(4-5):233-241
19 Conway C,Sharif F,Mcgarry JP,et al.A computational test-bed to assess coronary stent implantation mechanics using a populationspeci fi c approach.Cardiovascular Engineering and Technology,2012,3(4):374-387
20 Wang WQ,Liang DK,Yang DZ,et al.Analysis of the transient expansion behavior and design optimization of coronary stents by finite element method.Journal of Biomechanics,2006,39(1):21-32
21 王伟强,王丽,杨大智等.血管支架有限元优化设计.生物医学工程学杂志,2008,25(2):372-377(Wang Weiqiang,Wang Li,Yang Dazhi,et al.Optimization of vascular stent fi nite element method.Biomedical Engineering,2008,25(2):372-377(in Chinese))
22 Atherton MA,Bates RA.Robust optimization of cardiovascular stents:A comparison of methods.Engineering Optimization,2003,36(2):1-11
23 Harewood F,Thornton R,Ireland M.Step Change in Design:Exploring Sixty Stent Design Variations Overnight C.Altair Product Design Workshop,2011
24 Clune R,Kelliher D,Robinson JC,et al.NURBS modeling and structural shape optimization of cardiovascular stents.Structural&Multidisciplinary Optimization,2014,50(1):1-10
25 杜超凡,章定国.光滑节点插值法:计算固有频率下界值的新方法.力学学报,2015,47(5):839-847(Du Chaofan,Zhang Dingguo.Node-based smoothed point interpolation method:A new method for computing lower bound of natural frequency.Chinese Journal of Theoretical and Applied Mechanics,2015,47(5):839-847(in Chinese))
26 杜超凡,章定国,洪嘉振.径向基点插值法在旋转柔性梁动力学中的应用.力学学报,2015,47(2):279-288(Du Chaofan,Zhang Dingguo,Hong Jiazhen.A meshfree method based on radial point interpolation method for the dynamic analysis of rotating fl exible beams.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):279-288(in Chinese))
27 Li HX,Wang XY.Design optimization of balloon-expandable coronary stent.Structural&Multidisciplinary Optimization,2013,48(4):837-847
28 Li HX,Zhang YH,Zhu B,et al.Drug release analysis and optimization for drug-eluting stents.Scienti fi c World Journal,2013,2013(4):827-839
29 李红霞,王希诚.基于不同扩张模拟方式的支架优化设计.哈尔滨工业大学学报,2011(s1):267-272(Li Hongxia,Wang Xicheng.The stent optimization design based on di ff erent expansion simulation.Journal of Harbin Institute of Technology,2011(s1):267-272(in Chinese))
30 Pant S,Bresslo ffNW,Limbert G.Geometry parameterization and multidisciplinary constrained optimization of coronary stents.Biomechanics and Modeling in Mechanobiology,2012,11(1):61-82
31 Srinivas K,Nakayama T,Ohta M,et al.Studies on Design Optimization of Coronary Stents.Journal of Medical Devices,2008,2(1):121-136
32 Chua SND,Macdonald BJ,Hashmi MSJ.Finite element simulation of slotted tube(stent)with the presence of plaque and artery by balloon expansion.Journal of Materials Processing Technology,2004,155-156(6):1772-1779
33 Joseph VR,Hung Y.Orthogonal-maximin latin hypercube designs.Statistica Sinica,2012,18(1):171-186
OPTIMIZATION DESIGN OF DEGRADABLE POLYMER VASCULAR STENT STRUCTURE1)
Zhao Danyang*Liu Tao*Li Hongxia*,†,2)Wang Minjie*
*(School of Mechanical Engineering,Dalian University of Technology,Dalian116023,China)
†(National Joint Research Center for Micro-Forming Technology and Key Laboratory of Micro-molding of Henan Province,Zhengzhou University,Zhengzhou450001,China)
Due to the low sti ff ness of polymers,polymeric stent has lower radial support capability compared to metallic stent.Therefore,the width and thickness of the stent are usually increased to improve its radial support capability,which can not only reduce the fl exible performance of the stent and the area of the vascular lumen,but also increase the surface coverage and thus increase the risk of in-stent restenosis.In order to design polymeric stent with smaller strut width and thickness and improve its radial support capability,an optimization method combining with Kriging surrogate model and finite element method was used to optimize the geometries of stent.Kriging surrogate model was used to construct the approximate function relationship between design objectives and design variables.Optimized Latin Hypercube Sampling method was used to select the initial sample points.EI function was used to balance global and local search and tend to fi nd the global optimal solution.As an example,ART18Z polymeric stent was studied in this paper.Firstly,the strut width and thickness of the stent were respectively reduced by 0.02mm,and then the optimization method was used to optimize the key geometric parameters of ART18Z stent.The numerical results show that the overall service performance of ART18Z stent was improved after optimization and the proposed optimization method can be e ff ectively applied to the optimal design of the polymeric stent.
degradable polymer,vascular stent,mechanical performance,Kriging surrogate model,optimization design
R318.01
A doi:10.6052/0459-1879-17-214
2017–06–08 收稿,2017–09–11 录用,2017–09–11 网络版发表.
1)国家自然科学基金项目(11502044),中国博士后科学基金面上项目(2014M561222),国家级微纳成型技术国际联合研究中心与河南省微成型技术重点实验室联合开放基金项目(MMT2017-03)资助.
2)李红霞,副教授,主要研究方向:生物力学、结构优化设计.E-mail:hxli@dlut.edu.cn.
赵丹阳,刘韬,李红霞,王敏杰.可降解聚合物血管支架结构优化设计.力学学报,2017,49(6):1409-1417
Zhao Danyang,Liu Tao,Li Hongxia,Wang Minjie.Optimization design of degradable polymer vascular stent structure.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1409-1417
