基于遗传算法优化的双向垂直泊车路径规划∗
2017-12-18陈无畏方玉杰魏振亚
陈无畏,方玉杰,魏振亚
基于遗传算法优化的双向垂直泊车路径规划∗
陈无畏,方玉杰,魏振亚
(合肥工业大学汽车与交通工程学院,合肥 230009)
为了解决1段弧式垂直泊车对于泊车空间要求高的问题,本文中基于Ackerman转向原理建立了车辆前轮转向运动学模型。分析了泊车过程可能发生的碰撞问题并划分了垂直泊车起始区域,在此基础上规划了一种双向的3段弧泊车路径,并用遗传算法对规划的路径进行优化,在Matlab/Simulink中搭建仿真模型,对优化前后的路径进行仿真分析。结果表明所规划的3段弧路径能使车辆准确无误地停到目标车位,通过实车试验进一步验证了所提出的泊车路径规划方法的有效性和安全性。
垂直泊车;路径规划;遗传算法;仿真;优化;实车试验
前言
近几年,随着人口数量的增加,人民生活水平的提高和城市基础设施的不断扩张,汽车的保有量逐年增加,有限的城市空间变得越来越拥挤,停车难问题变得日益凸显。因此,开发自动泊车系统(automatic parking system,APS),可将驾驶员从复杂的泊车操作中解脱出来,提高驾驶的舒适性,缓解驾驶员泊车时的紧张程度,预防泊车事故的发生。
自动泊车理论研究的一个关键部分是路径规划,对此,国内外的许多学者已进行了大量的研究。文献[1]中采用模糊控制的策略,提出了多向移动式的泊车路径规划方法。文献[2]~文献[4]中分别提出了使用5次多项式曲线、β-spline曲线和回旋曲线作为汽车的泊车路径,这3种曲线都是曲率连续变化的光滑曲线。文献[5]中提出了一种基于两步法逼近的分段式路径规划,这种方法总体上比其它路径规划方法简单,但过于依赖对起始位置的优化,并不适合实际应用。文献[6]中提出了一种单向多次和双向多次的路径规划方法,但仿真结果对于车位的长度要求依然较高,最短车位长度都已接近7m。文献[7]中通过2段圆弧相切进行路径规划,虽然能缩短路径,但单向路径曲率不连续。文献[8]中提出了一种基于2段弧式的垂直泊车路径并进行跟踪,但这种方法可能无法完成车位的检测。
为解决上述研究存在的过度依赖起始位置优化、单向曲率不连续和车位检测缺陷等问题,本文中提出了一种基于车位检测的双向3段弧垂直路径规划方法,该方法能有效扩大垂直泊车的初始停车区域,并借助于遗传算法进行二次规划,可进一步通过优化缩短所规划路径的总长度。仿真和实车试验的结果都验证了该路径规划方法的有效性和可行性。
1 车辆运动学模型
泊车时一般车速在6km/h以下,由此假定无侧滑现象,在此基础上建立车辆的运动学模型,如图1所示。

图1 车辆运动学模型
图1 中,Q和P分别为车辆前、后轴中心点,v为前轴中心点速度,L为目标车辆轴距,LC为后轴轮距,α为车身与x轴的夹角,β为前轮对应的转向角。因为后轮轨迹在车辆垂直方向速度为0,其方程为

由图可知,车辆前轮中心与后轮中心的坐标关系为

由式(1)和式(2)可得速度关系为


从而可得

由式(1)~式(4)可得车辆后轴中心点的运动轨迹方程为
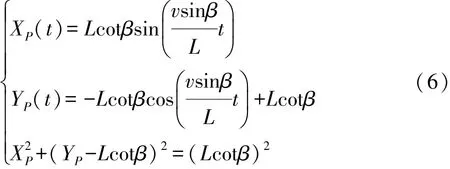
2 垂直泊车碰撞分析
在进行泊车路径规划之前,须先分析泊车过程中的碰撞问题,这也是设计一条无碰撞路径的关键所在。根据垂直泊车经验可知,垂直泊车过程中可能发生的碰撞点主要集中在目标车位的左右两个边界,如图2所示,将转向盘向右打死进行垂直泊车。其中点O,P和Q分别为最小转弯半径的圆心、后轴中心点和前轴中心点;点A,B,C和D分别为车辆4个车轮中心在地面的投影点;点E,F,G和H分别为车辆4个顶点在地面的投影点。
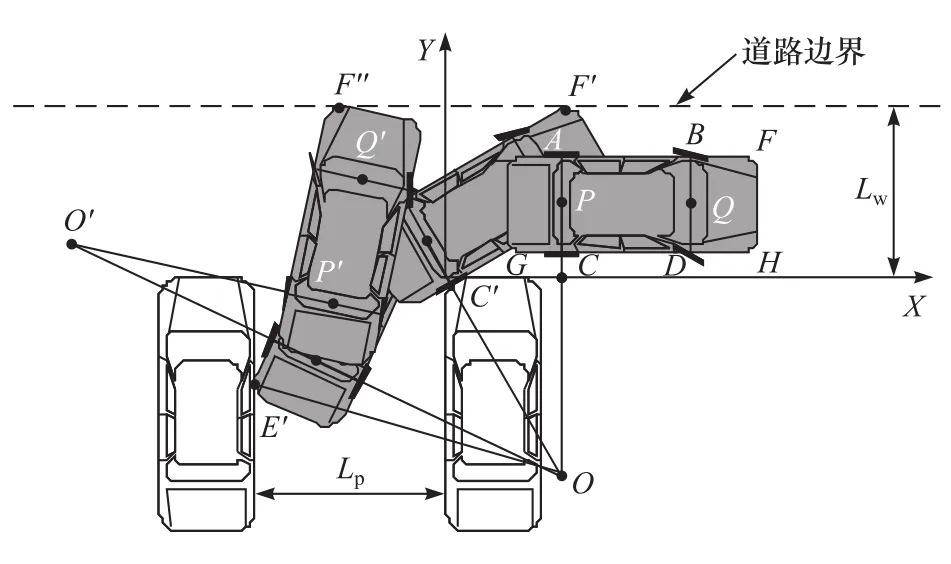
图2 垂直泊车碰撞示意图
2.1 车位右侧边界防碰撞分析
分别将点A,B,C,D,E,F,G 和H 与点O 进行连线,可以发现OC连线最短,而最容易与车位右侧边界发生碰撞的就是点C,C′是与C相对应的临界碰撞点。以车位右侧边界最上方的边界点为原点,建立X-Y直角坐标系,点P(XP,YP)为泊车起始点,分析C-C′的临界碰撞过程,并根据几何关系可得考虑到泊车过程属于低速运动,可认为车轮不发生侧滑,因此可以认为后轮做圆周运动,故有以下关系式:


根据P点坐标,可确定另外两条直角边的长度为

根据以上公式推导,可得车辆与右侧边界临界碰撞时的约束关系式为

不发生碰撞的条件为

根据汽车轮廓参数可得

且因:

故可得车位右侧边界无碰撞条件为

2.2 车位左侧边界防碰撞分析
同理,由图2可知,车辆的E点最容易与车位左侧边界发生碰撞,当车辆按照圆周运动进入车位后,碰撞的临界条件考虑为车体E′点刚好与车位左侧边界擦过,故应满足约束方程:

又因:

由式(17)~式(19),可得不发生碰撞的条件为

式中:Lp为车位宽度;Lr为车辆后悬长度。
2.3 车辆左侧与道路边界防碰撞分析
由图2可见,为避免车辆与道路边界障碍物或对面车道行驶的车辆发生碰撞,车身轮廓左前点F应该不能越过道路边界线。整个过程中,最有可能发生越过道路边界线的情况主要有两处:一处是倒车入库时的点F′;另一处是前进调整姿态的点F″。
倒车入库时的临界条件为

又因:
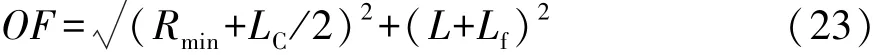
综合式(22)和式(23),可得点F′不越过道路边界的条件为
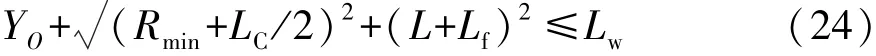
式中:YO为圆心O点的纵坐标;Lf为车辆前悬长度;Lw为泊车通道最小宽度。
前进调整姿态时的临界条件为

式中σ为P″F″与Y轴的夹角。因0≤cosσ≤1,故式(25)条件可放宽为
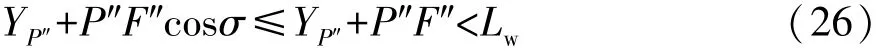
又因:

综合式(26)和式(27)可得

式中YP″为前进调整时后轴中心点的纵坐标。
3 垂直泊车路径规划
根据垂直泊车的流程,当车位检测结束,确定泊车类型后,根据此时的停车位置,划分泊车的起始区域,进而规划可行路径,其中后轴中心点的轨迹如图3所示,图中相关参数说明如表1所示。
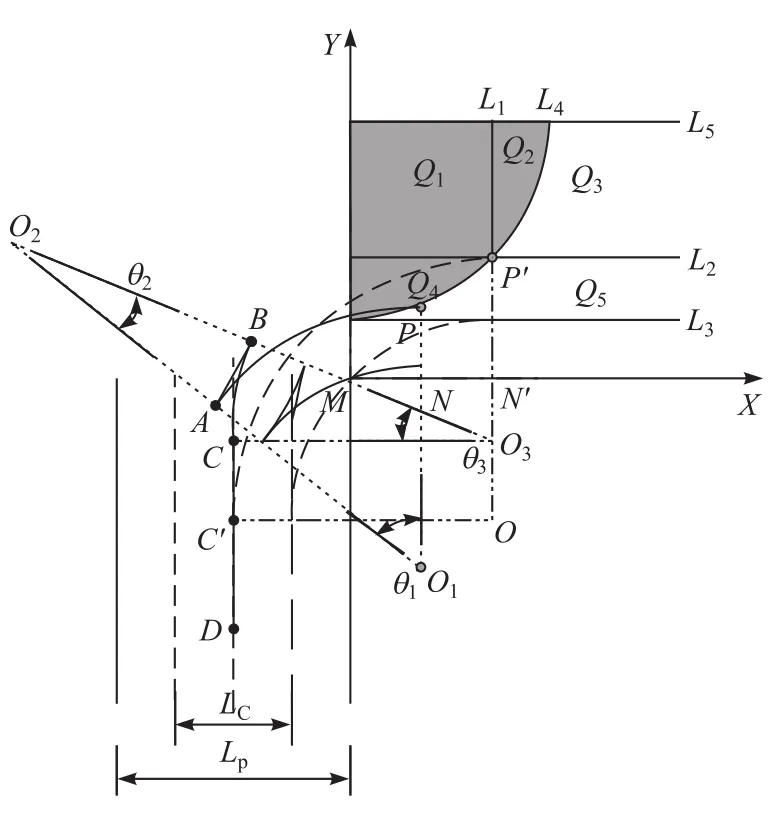
图3 车辆后轴中线点轨迹示意图
3.1 起始区域划分
起始区域作为泊车路径的起始点,不仅决定着路径规划的复杂程度,而且影响着整个泊车的效果及其成败,所以起始点的确定,是路径规划中至关重要的一环。为降低区域规划的复杂程度和实车试验时的执行难度,本文中规划的路径都是基于车辆最小转弯半径Rmin实现的。由图3可见,主要有两种路径类型:1段弧式路径和3段弧式路径。

表1 图3相关参数说明
通过对两类路径类型的临界情况分析,可得L1,L2,L3,L4和L55条边界线,其中L1和L2由1段弧式倒车入库的临界情况计算得到,L4由3段弧路径临界情况计算得到,L5和L3分别决定了起始点纵向坐标的上下界限。
如果目标车辆沿着弧P′C′进行单段弧模式泊车,当右侧车轮刚好同车位右侧边界顶点临界碰撞时,由几何关系可得

所以L1和L2对应的直线方程分别为

如果目标车辆沿着弧PA,AB和BC进行3段弧模式泊车,当右侧车轮刚好同车位右侧边界顶点临界碰撞时,根据直角ΔO1MN可得

L3对应的直线方程为

设P点为动点,可得L4对应的曲线方程为

又因为需要保证倒车入库时车辆的左前顶点不会越过车道线的边界,即

又因:

可得
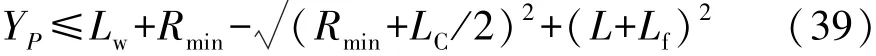
即L5对应的直线方程为

根据JGJ100—98《汽车库建筑设计规范》中的表4.3.4可知,对于小型车垂直式泊车,其泊车通道最小宽度Lw为6m。
根据式(31)、式(32)、式(34)、式(36)和式(40)可将起始区域划分为 Q1,Q2,Q3,Q4和 Q55 块区域,如图4所示。Q1,Q2和Q3区域对应的是1段弧式垂直泊车,Q4和Q5对应的是3段弧式垂直泊车。当起始点位于Q1区域时,须先前进至边界L1附近,然后执行1段弧式垂直泊车;当起始点位于Q2和Q3区域时,须先后退至边界L1附近,然后执行1段弧式垂直泊车。当起始点位于Q4区域时,可直接执行3段弧式垂直泊车,位于Q5区域时,需要先后退至Q4区域内,再执行3段弧式垂直泊车。综上所述,3段弧式垂直泊车有效地解决了泊车起始位置位于L2与L3之间区域的问题,扩大了垂直泊车的有效起始停车区域。
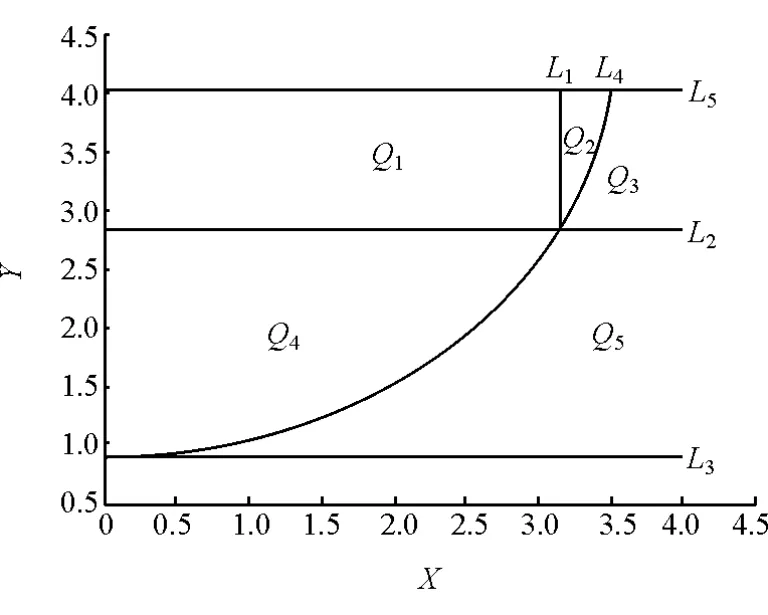
图4 起始位置区域划分
3.2 路径规划
如图3所示,进行3段弧式垂直泊车时,从起始点P开始,首先将转向盘向右快速打到最小转弯半径Rmin对应的极限位置并挂倒车挡后退,当后轴中心点到达车位中心线上的A点时,再将转向盘快速打到左极限位置并挂前进挡前行,当后轴中心点到达位置B点时,再将转向盘快速打到右极限位置并挂倒车挡后退,当后轴中心点轨迹与车位中心线相切于C点时,此时快速回正转向盘并沿着车位中心线倒车,当后轴中心点到达目标后轴中心点D时,停车并结束泊车。
分析第1段弧PA,根据已知参数和几何约束可得
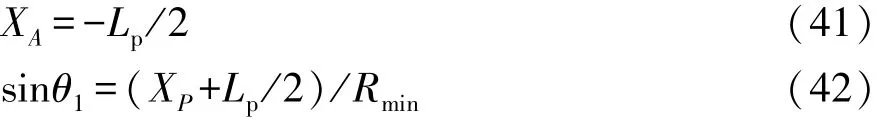
所以有

分析第2段弧AB,根据各点横坐标的关系可得

所以有

分析第3段弧BC,根据各点横坐标的关系可得

已知 XC=XA,代入式(50)可得

3.3 二次路径规划
车位检测结束并停车后,通过外部传感器可获取后轴中心点的起始坐标,根据第3.2节中的路径规划内容,可规划出对应的弧长和角度,并通过路径跟踪控制目标车辆安全准确地停到目标车位内。成功进行垂直泊车的目标除了准确无误且无碰撞地将目标车辆停到目标车位内外,尽可能短的总路径长度也是不可忽略的目标之一。另外,除第2.1,2.2和2.3节中对车位两边界和车道线边界的碰撞分析外,考虑到完成泊车时要求车辆中心线与车位中心线完全重合过于严苛,所以放宽约束条件,以最终后轴中心点位于车位中心线左右两侧0.1m以内作为成功泊车条件之一。
本文中采用遗传算法对路径进行二次规划,因为遗传算法无须给出优化变量的初始值,只须给出优化变量的范围即可进行高效并行的全局搜索,并且遗传算法无需目标函数的导数梯度等信息,按照适应度的值即可搜索最优值。遗传算法对于许多线性、非线性、等式和不等式约束问题的解决策略主要有:拒绝策略、修复策略和惩罚策略等。惩罚函数法因执行简单而得到了广泛的应用,其主要思想是通过对目标函数f(x)增加惩罚项p(x)来构造惩罚适应值函数F(x),从而将约束优化问题转化为无约束优化问题进行求解,其中个体违反约束条件的程度由惩罚函数确定,大多数采用如下惩罚项函数:

来表示个体x与第j个约束条件的距离,则

表示个体x与可行域边界距离的总和,也反映了个体x违反约束条件的程度。其中,nj(x)表示第j个不等式约束,ej(x)表示第j个等式约束,m表示不等式约束条件的个数,(s-m)表示等式约束条件的个数。惩罚函数确定之后,结合目标函数,即可建立相应的个体适应度函数:

式中λj为第j个约束函数的惩罚系数。
本文中结合目标函数和约束条件,可得以下适应度函数:
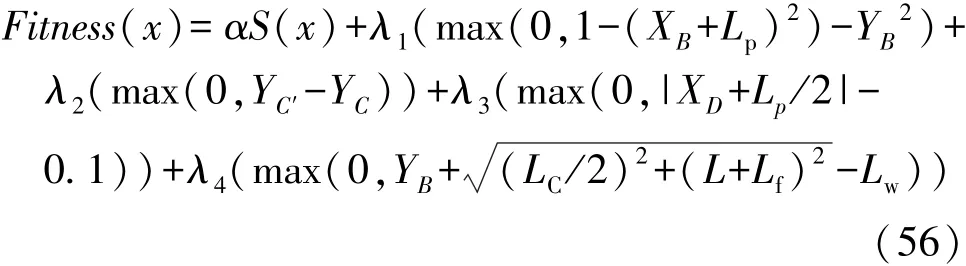
取 α=1,λ1=8,λ2=26,λ3=18,λ4=30,运用Matlab/Gatool工具箱,编写适应度函数对应的M文件,并设置相关参数,结果是:起始点(1,1.5)优化后,拐点A和B的横坐标分别为-0.75和0.29;而起始点(2,2.5)优化后,拐点A和B的横坐标分别为-0.56和-0.12。
基于此横坐标,再结合前面3.2节中路径规划的内容,可分别确定二次规划对应的3段弧长和角度,进而获得完整的泊车路径。
4 仿真与实车试验
4.1 仿真结果分析
根据建立的车辆运动学模型,在Matlab/Simulink中搭建仿真平台,仿真参数如表2所示,仿真结果如图5~图8所示。

表2 泊车相关的仿真参数 m

图5 起始点为(1,1.5)的仿真图
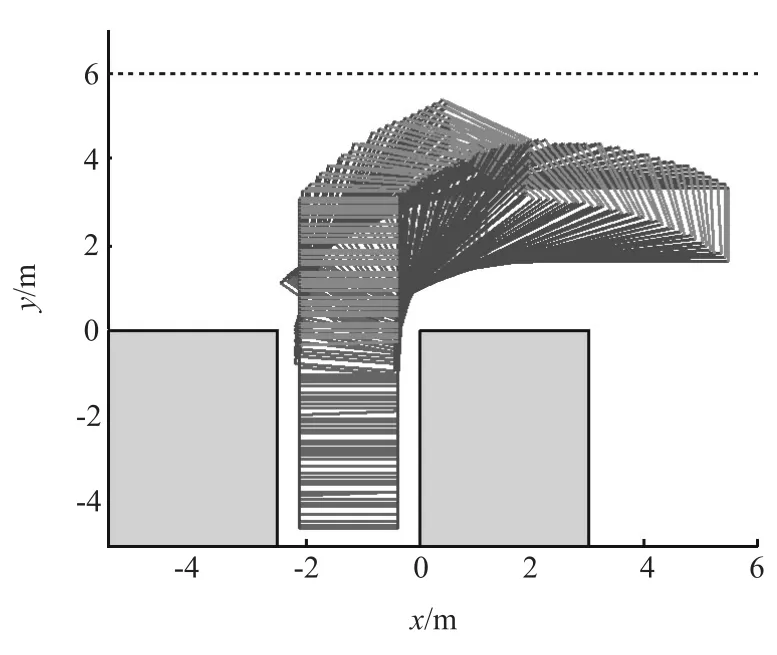
图6 起始点为(2,2.5)的仿真图
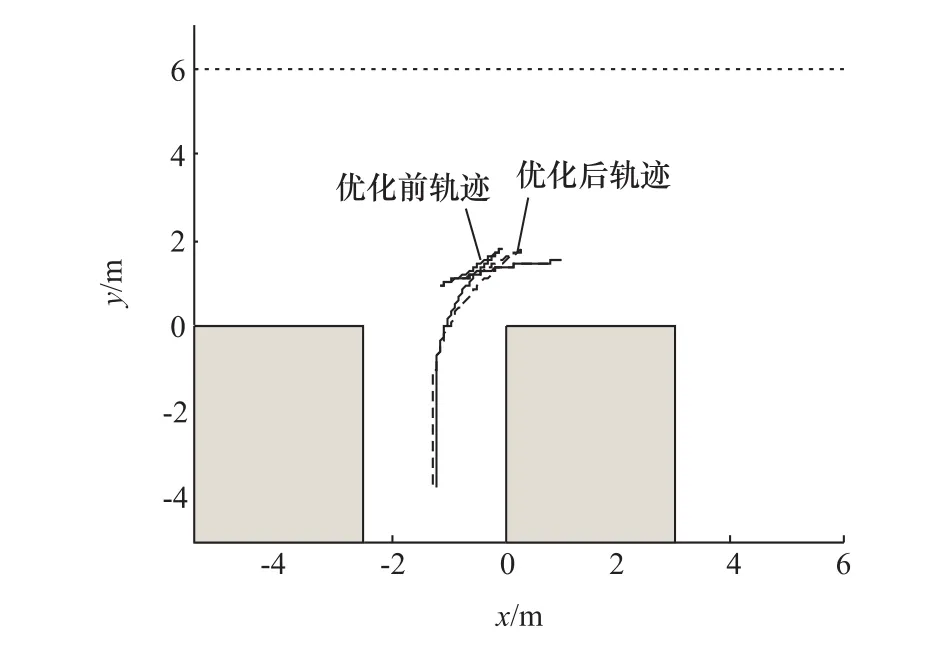
图7 起始点为(1,1.5)的二次规划前后轨迹对比图

图8 起始点为(2,2.5)的二次规划前后轨迹对比图
分别选取点(1,1.5)和(2,2.5)作为目标车辆后轴中心起始点,通过图5和图6的仿真结果可知,目标车辆在完成3段弧式垂直泊车的整个过程中,都没有与车位边界发生碰撞,车头也始终没有越过道路边界线,且泊车结束后,目标车辆与左右车辆之间的间距合适。图7为后轴中心起始点坐标为(1,1.5)时二次规划前后轨迹对比图,二次规划前路径总和为 9.660 4m,二次规划后的路径总和为9.197 0m,路径总和缩短了4.8%,泊车过程中,当目标车辆位于拐点B时,此时后轴中心点与道路边界线的纵向偏差ΔY=4.2m,大于车辆后轴中线点与车辆左前顶点3.6m的直线距离,即车辆始终处于道路边界内,泊车结束后,后轴中心点与车位中心线的横向偏差ΔX=0.066m,也处于0.1m以内的约束范围;图8为后轴中心起始点坐标为(2,2.5)时二次规划前后轨迹对比图,二次规划前路径总和为10.444 4m,二次规划后的路径总和为9.868 4m,路径总和缩短了5.5%,泊车过程中,当目标车辆位于拐点B时,此时后轴中心点与道路边界线的纵向偏差ΔY=3.9m,同样大于车辆后轴中线点与车辆左前顶点3.6m的直线距离,即车辆同样始终处于道路边界内,泊车结束后,后轴中心点与车位中心线的横向偏差ΔX=0.085m,同样也处于0.1m以内的约束范围。
4.2 实车试验
试验车为某小型SUV,根据 JGJ100—98《汽车库建筑设计规范》第4.1.1,4.1.5.3和4.1.4规定可知,小型车需要的最小垂直车位尺寸为5.8m×3.0m(长×宽)。考虑到现如今城市车位紧张,很多车位无法达到标准尺寸,故通过左右实车搭建5.5m×2.8m的真实垂直车位进行实车验证[10]。实车试验的硬件平台组成主要有:装有自主研发EPS控制器的试验车一辆、自主开发的APS控制器、若干超声波雷达、两路测速编码器、一个语音提醒模块、一套VBOX试验箱和一台计算机。主要的信号流向和通信方式如图9所示。

图9 实车试验信号图
在泊车过程中,路面为平坦干燥水泥路面,整个泊车区域内没有其它动态和静态障碍物,且实车测试驾驶员相同,垂直泊车流程大致如下:目标车辆寻找车位时,安置在侧方位的雷达实时采集横向距离,通过一次下降沿突变和一次上升沿突变可确定车位两侧边界,若车位符合泊车要求,此时语音模块提醒驾驶员停车并开启泊车开关,泊车控制器计算泊车起始点并进行路径规划,泊车过程中实时检测车辆行驶的实际弧长并与理论弧长进行比较,并以此为基础来控制EPS控制器进行自动转向,在拐点时,语音模块会提醒驾驶员停车并换挡,图10为双向垂直泊车的实车试验现场图。

图10 双向3段弧式垂直泊车试验图
实车试验中,选取后轴中心起始点坐标为(2,2.5),分别进行8组试验并记录,统计泊车结束后目标车辆左右后轮分别与车位左右边界的距离、目标车辆中心线与车位中心线的夹角和泊车过程中是否发生碰撞。结果如表3所示。
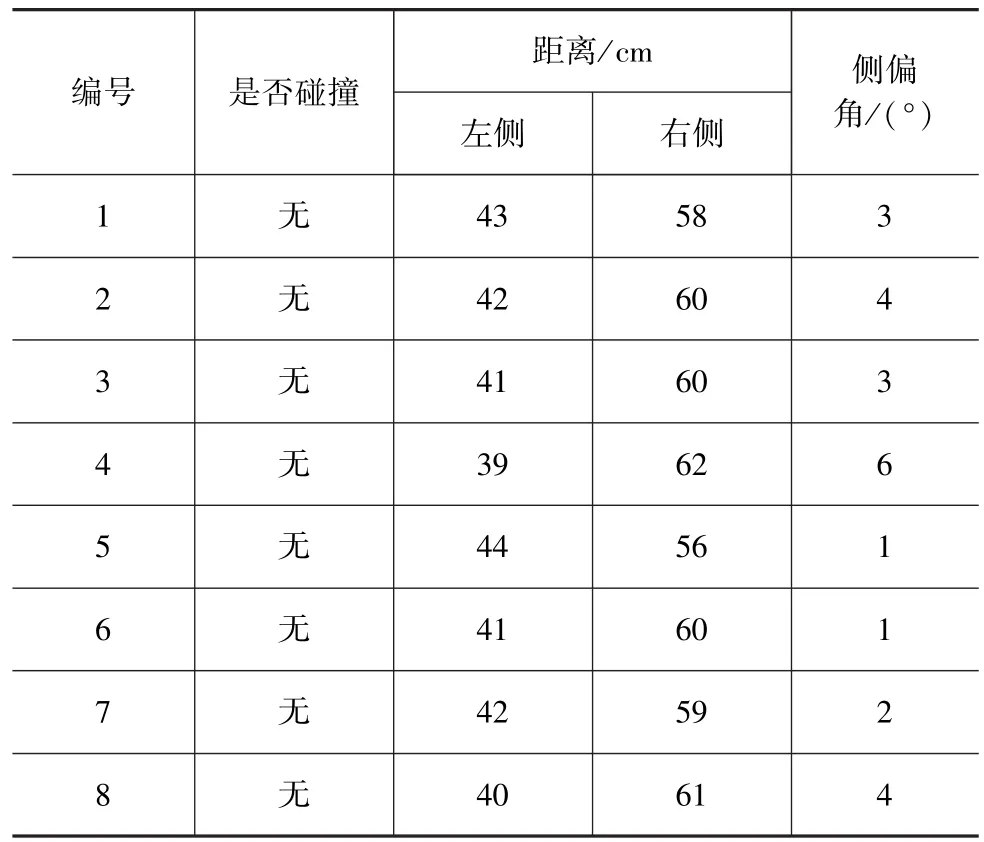
表3 双向3段弧式垂直泊车试验结果
由表3可知,8组泊车试验均未发生碰撞,车身与车位中心线的侧偏角最大为6°,没有超过10°,处于可接受范围之内。通过左右距离对比可以发现,左侧距离普遍小于右侧距离,同样符合二次规划后车辆后轴中心点最终位于车位中心线左侧的仿真结果,另外,大部分实车试验的后轴中心点横向偏差略大于仿真结果,分析原因可能是泊车过程中,由于转向系统自回正力矩的存在,导致实际的转弯半径略大于理论的转弯半径。根据VBOX采集的GPS数据,经过高斯投影坐标转换,获取实车试验的离散坐标点,本文中选取第5次的实车试验轨迹同仿真计算轨迹对比,结果见图11,其关键点数据见表4。
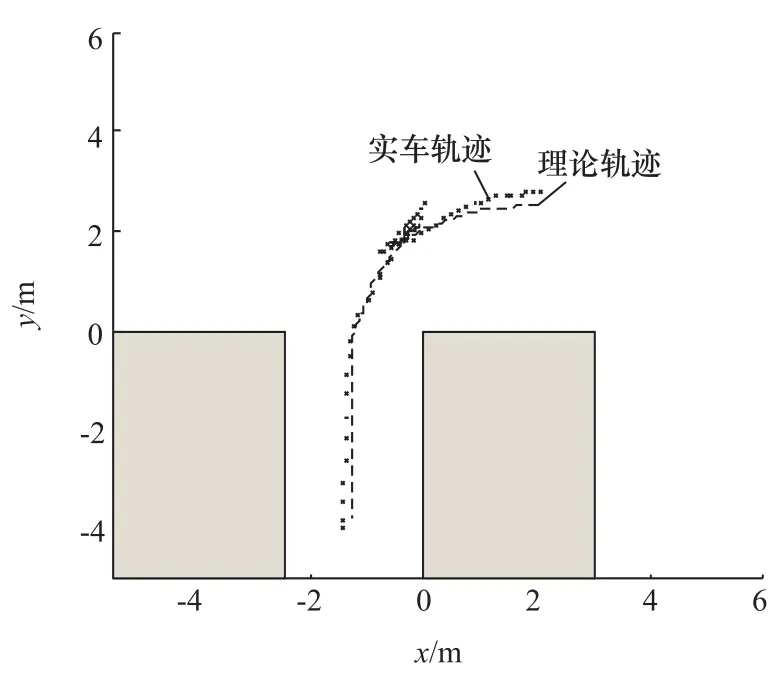
图11 实车轨迹与仿真轨迹对比图
由图11可以看出,实车基本上沿着理论轨迹进行泊车,出现误差较大的地方主要有3处,分别为泊车起始位置、第1次拐点处和第2次拐点处。
分析表4中关键点的坐标误差,其中起始位置误差主要由侧方位雷达精度不高造成,两次拐点处的误差主要由于驾驶员不能及时停车换挡造成,所以容易导致实车轨迹的前2段弧长比理论上的弧长大,停车点相对理论停车点,入库深度更大,主要由于驾驶员未能及时停车所致。

表4 实车轨迹与仿真轨迹关键点数据对比
5 结论
(1)结合实际泊车过程,分析碰撞约束条件,并以此划分泊车初始区域,分别规划单向1段弧式垂直泊车路径和双向3段弧垂直泊车路径,仿真结果表明所规划路径符合泊车要求。
(2)基于遗传算法对所规划的3段弧路径进行二次规划,二次规划后的路径依然满足泊车过程中的碰撞约束并能正常泊入车位,且总路径长度都有所缩短。
(3)在实车试验中,考虑到外部传感器、APS控制器和EPS系统在工作过程中存在的偶然误差,特别是驾驶员不能及时在路径拐点停车换挡,造成实际路径与理论路径之间的误差。实践表明,本文所述路径规划方法可在工程中实现。
[1] SÁNCHEZ C M, PEÑASM S,SALVADOR L G.A fuzzy decision system for an autonomous car parking[M].Handbook on Decision Making.Springer Berlin Heidelberg,2012:237-258.
[2] ZHANG S,SIMKANIM,ZADEH M H.Automatic vehicle parallel parking design using fifth degree polynomial path planning[C].IEEE Vehicular Technology Conference,2011:1-4.
[3] MAEKAWA T, NODA T, TAMURA S, et al.Curvature continuous path generation for autonomous vehicle using B-spline curves[J].Computer-Aided Design,2010,42(4):350-359.
[4] VOROBIEVA H,GLASER S,MINOIU-ENACHE N,et al.Automatic parallel parking in tiny spots:path planning and control[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(1):396-410.
[5] CHENG K,ZHANGY,CHEN H.Planning and control for a fullyautomatic parallel parking assist system in narrow parking spaces[C].Intelligent Vehicles Symposium, IEEE,2013:1440-1445.
[6] 侯晓阳,黄勇,孙思,等.多约束平行泊车路径规划[J].汽车技术,2015(9):48-52.
[7] 姜辉,郭孔辉,张建伟.基于路径规划的自动平行泊车转向控制器[J].吉林大学学报(工学版),2011,41(2):293-297.
[8] 陈佳佳,梅涛,祝辉.基于路径规划和双闭环控制的泊车系统研究[J].电子测量技术,2011,34(3):20-24.
[9] 陈广洲,解华明,鲁祥友.Matlab遗传算法工具箱在非线性优化中的应用[J].计算机技术与发展,2008,18(3):246-248.
[10] 朴昌浩,张乐,张艳,等.非平行初始状态自动泊车轨迹生成方法[J].北京理工大学学报,2014(5):506-511.
Path Planning of Two-direction Vertical Parking Based on Optimization with Genetic Algorithm
Chen Wuwei, Fang Yujie& Wei Zhenya
School of Automotive and Transportation Engineering, Hefei University of Technology, Hefei 230009
To solve the problem of high demand for parking space in one-arc vertical parking,a steering kinematics model for vehicle's front wheel based on Ackerman steering principle is established.Then the possible collisions in parking process are analyzed and the initial area for vertical parking is divided into several sub-areas.On this basis,a two-direction three-arc parking path is planned and optimized by using genetic algorithm.Finally a simulation model is built with a simulation conducted to compare the lengths of parking paths before and after optimization.The results show that the three-arc parking path planned can make a vehicle accurately stop on target parking berth,and real vehicle tests further verify the effectiveness and safety of the parking path planning scheme proposed.
vertical parking; path planning; genetic algorithm; simulation; optimization; real vehicle test
10.19562/j.chinasae.qcgc.2017.11.016
∗国家自然科学基金(U1564201,51375131和51675151)资助。
原稿收到日期为2016年11月11日,修改稿收到日期为2017年1月2日。
陈无畏,教授,博士生导师,E-mail:hfgdcjs@ 126.com。
