基于结构分析法的故障诊断理论及其应用研究∗

陈 奇，姚志刚， Qadeer Ahmed，张 振，贺良国

基于结构分析法的故障诊断理论及其应用研究∗

陈 奇1，姚志刚1， Qadeer Ahmed2，张 振1，贺良国1

(1.合肥工业大学机械工程学院，合肥 230009； 2.美国俄亥俄州立大学汽车研究中心，美国哥伦布 43212)

为最大化系统的故障诊断能力，快速实现故障诊断系统设计，应用了基于结构分析法(SA)的故障诊断理论，其主要步骤为：利用失效模式与影响分析(FMEA)获得系统的关键故障，建立其故障模型；通过DM分解和FIM分析，进行系统的故障可检测性和故障可隔离性评估；结合最小型超定方程集(MSO sets)，并基于解析冗余关系(ARR)和观测器的参数评估方法，实现系统的残差设计。最后以一款AMT换挡执行器为例，利用SA方法对其进行故障诊断能力分析和FDI系统设计，并在MATLAB/Simulink中对FDI系统进行仿真，验证其有效性。

AMT换挡执行器；故障诊断；结构分析；DM分解；FIM分析

前言

随着汽车工业的快速发展，汽车故障诊断技术已成为汽车工业发展的重要组成部分。故障诊断的主要任务有故障检测、故障隔离和故障的评价与决策[1]。故障诊断方法分为3大类[2]，分别为基于模型的故障诊断、基于信号处理的故障诊断和基于知识的故障诊断。

根据残差产生形式的不同，基于模型的故障诊断方法[3]又可细分为参数估计法[4-6]、状态估计法[7-11]和等价空间法[12-15]。但这3种方法缺少故障诊断能力的评估，很难获得最大化的故障诊断能力；同时，在进行残差设计时，设计算法繁琐、效率较低。以上不足将导致故障诊断效率低，故障误诊和漏诊。

近年来，国外学者提出了一种故障诊断新方法——结构分析法(structural analysis，SA)，该方法不依赖于具体的数值参数，只取决于系统的结构模型，能快速地分析复杂系统中的故障可诊断性和可隔离性，设计算法简单，可有效提高故障诊断效率，避免故障误诊、漏诊。有关结构分析法(SA)的主要研究有：1989年文献[16]中首次提出结构分析法的概念；1994年文献[17]中对结构分析法中Dulmage-Mendelsohn(DM)分解技术进行了研究；1997年文献[18]中应用结构分析法对非线性系统进行故障冗余分析；2000年文献[19]中基于结构分析法进行了故障容错控制系统设计；2002年文献[20]和文献[21]中对结构分析法进行了详细论述，并给出了应用实例；2003年文献[22]中对结构分析法的可隔离性(fault isolability，FI)分析理论进行了较大改进；2006年文献[23]中对伺服阀系统进行故障诊断性分析；2008年文献[24]中提出一种有效获得最小型超定方程集(minimal structurally over-determined sets，MSO sets)的有效计算策略；2010年文献[25]中在基于模型的故障诊断中，使用含有混合因果关系的计算序列产生故障诊断的残差，并运用于汽车系统；2013年文献[26]中提出基于模型的残差生成的方法和数据驱动的残差统计评价方法，并运用于汽车发动机的故障诊断和隔离；2014年文献[27]中提出一种可实现连续残差设计的方法，可有效提高故障诊断检测和隔离的效率，并在混合动力汽车中进行验证；2015年文献[28]中利用结构分析法，推导出一套用于故障检测和隔离的解析冗余关系，用于电动汽车的故障诊断。2016年文献[29]中应用结构分析法对一款变速器的传动系统进行了故障诊断系统设计。

本文中将介绍结构分析法的故障诊断理论，并以一款AMT换挡执行器故障诊断为例阐述具体应用方法：首先，通过失效模式及影响分析(failure modes and effects analysis，FMEA)获得其关键故障，引入故障变量，建立换挡执行器的故障模型；其次，利用DM分解和故障隔离矩阵(fault isolation matrix，FIM)对换挡执行器进行故障可检测性和隔离性分析，通过增加变速杆位移传感器和电流传感器可实现关键故障的最大可检测性与可隔离性；然后，确定结构最小型超定方程集(MSO sets)用于产生残差；接着，利用解析冗余关系(analytical redundant relation，ARR)和基于观测器参数评估的方法，设计4个具有稳定性的残差；最后，选取合适的固定值作为残差的阈值，在MATLAB/Simulink仿真环境中进行残差验证，测试和校验故障与隔离(fault detection and isolation，FDI)系统设计的有效性。

1 结构分析法理论简介

1.1 结构分析法

结构分析法(SA)是一种新型的故障诊断方法，属于基于模型的故障诊断方法。它是一种利用图形工具，实现系统的故障可检测性和可隔离性能力评估，并可构建结构最小型超定方程集(MSO sets)，用于残差设计，实现故障的检测和隔离；同时也可用于容错控制的可重构性分析；也可进行传感器的布置方案设计，实现最优化的故障可隔离性和可检测性[30-31]。

1.2 结构分析法(SA)应用步骤

结构分析法的应用可归纳为如下6个步骤：

(1)关键故障获取 通过对系统的结构分析后，利用FMEA归纳总结系统各部件的故障模式、故障引起的影响和故障产生的原因，并对各个故障进行风险优先级顺序评估，获取系统的关键故障；

(2)故障模型创建 根据已获得的关键故障种类和特征引入关键故障变量，将关键故障变量与系统数学模型融合建立系统的故障模型，并获得系统的结构表征图(structural representation)；

(3)故障分析 利用DM分解、故障隔离矩阵等方法，分析故障的可检测性(fault detectability，FD)和可隔离性分析；

(4)结构最小型超定方程集生成 重复使用DM分解，分析系统的结构超定部分，确定结构最小型超定方程集，用于序列残差(residual)的生成；

(5)残差设计 利用解析冗余关系和观测器参数评估方法，进行序列残差设计；

(6)诊断策略确定 根据序列残差的特性，选取合适的结构最小型超定方程集，设计合适的阈值，确定诊断策略。

具体过程如图1所示。

2 实例应用

机械式自动变速器(AMT)是在MT变速器基础上，利用换挡执行机构代替人工换挡，实现自动换挡的一种变速器。换挡执行器是保证AMT正确换挡的重要组成部件，如果其发生故障，将会造成AMT无法正常换挡。

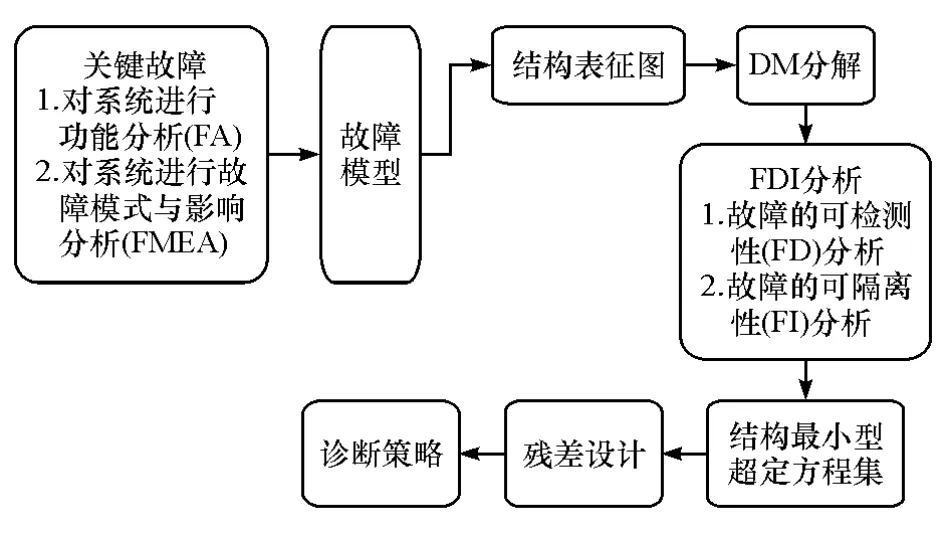
图1 结构分析法的使用步骤

图2 为线性执行机构的结构图，主要由电机、轮系、进给丝杆、推拉绳和两个转动杆构成。电机动力由这些部件传至换挡手柄实现换挡。AMT中有两个线性执行器，由于这两个线性执行器的结构完全相同，所以本文中取其中一个线性执行器作为研究对象。

图2 AMT线性执行机构结构图

2.1 线性执行器故障模型

由文献[32]可知，通过对换挡执行器进行故障模式和影响分析，可获取换挡执行器的关键故障，如表1所示。

表1 线性执行器的关键故障

将上述关键故障参数化后，并引入到换挡执行器的数学模型中，即可建立换挡执行器的故障模型：

式中：e1，e2，e3和 e4分别代表方程 1、方程 2、方程 3和方程4，下同；其他量含义如表2所示。

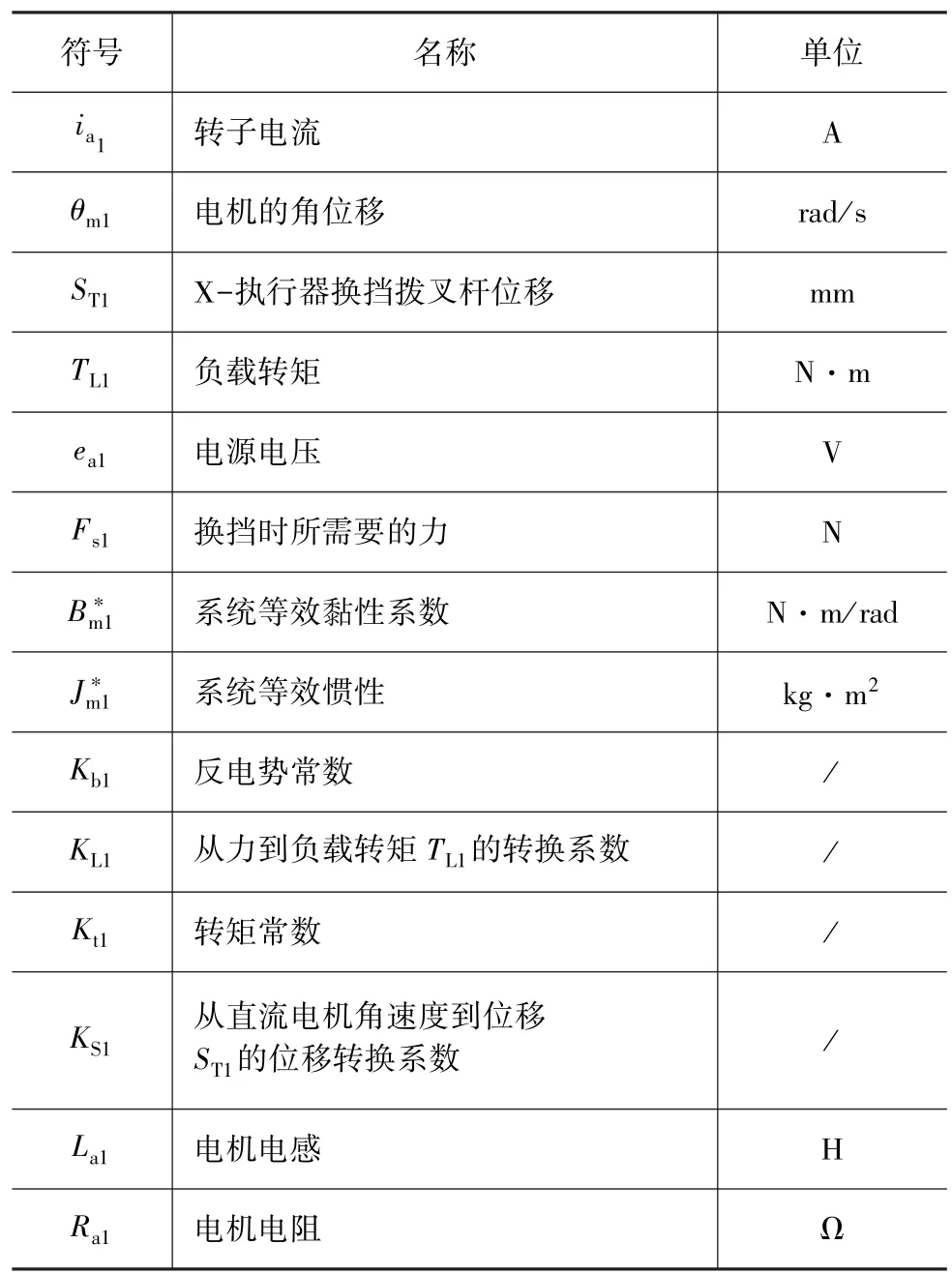
表2 符号含义及其单位

2.2 线性执行器结构表征图

结构表征图是一种能够表达系统结构的二分图[33]。将式(1)故障模型中的变量分为3类：未知变量{ia1，θm1，TL1，ST1}、已知变量{ea1，Fs1}和故障变量{fRa1，fKC1，fFS1}，即可得到线性执行器的结构表征图，如图3所示。图中，“×”表示等式ei与对应的变量存在关联关系。

2.3 DM分解

DM分解是一种将一个形似上三角形式的稀疏矩阵进行列和行重新排列的数学工具，并可将系统模型分为3个不同的区域[34]，如图4所示。

(1)结构欠定部分M-，即未知变量的数目多于方程数；

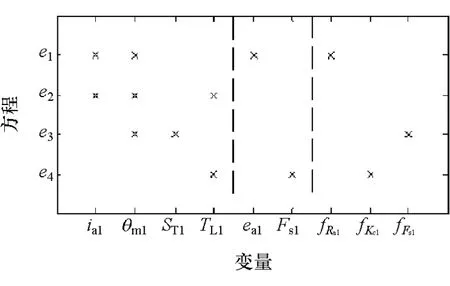
图3 换挡执行器的结构表征图

(2)结构正定部分M0，即未知变量的数目等于方程数；

(3)结构超定部分M+，即未知变量的数目少于方程数。

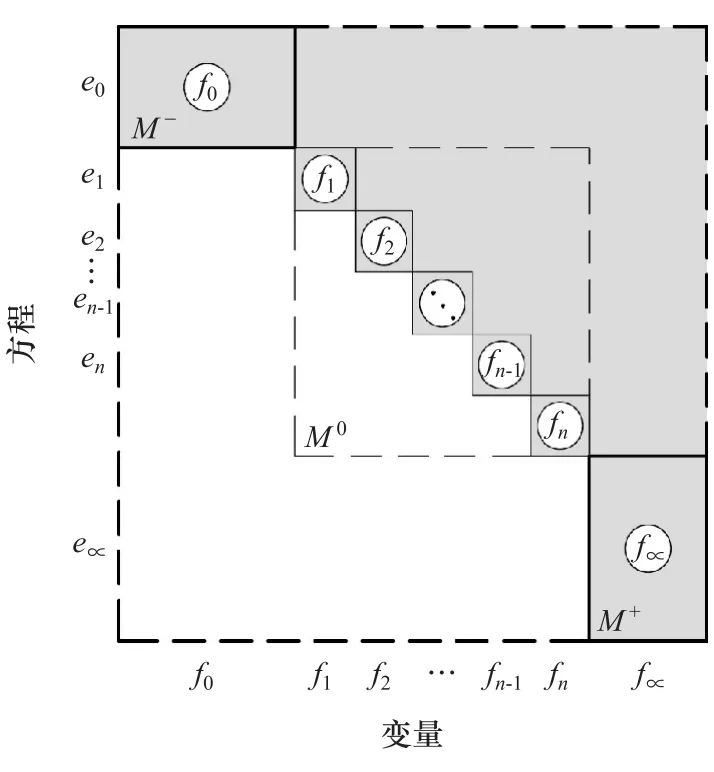
图4 DM分解区域

由文献[35]可知，如果方程中的故障f位于结构超定部分M+，即ef∈M+，则说明该故障f是可检测的。

图5 AMT线性执行机构DM分解图

图5 给出了换挡执行器的故障模型的DM分解图，结果显示当换挡执行器中在没有传感器时，所有的关键故障都不可检测，因为此模型经DM分解后，没有结构超定部分。

2.3.1 故障可检测性(FD)分析

为使所有的关键故障都能被检测到，须在换挡执行器中增加传感器。式(2)和式(3)分别给出了增加电机输出轴处的角位移传感器(θm1)和换挡拨叉杆位置的位移传感器(ST1)后的故障模型。

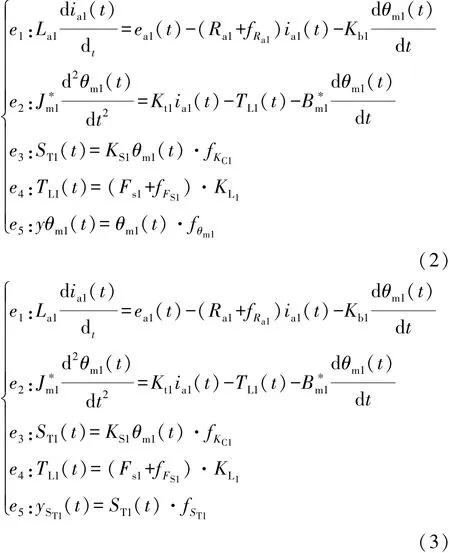
式中：fST1和 fθm1为传感器故障变量；yST1和 yθm1为测量值。

对式(2)和式(3)的故障模型分别进行DM分解，结果如图6所示。

图6 增加不同传感器的DM分解图

由图6可见，增加位移传感器(ST1)的结果较角位移传感器(θm1)好，因为前者可检测出所有的故障，而后者不能检测出推拉绳故障(fKC1)。

2.3.2 故障可隔离性(FI)分析

故障隔离性(fault isolability，FI)指当该故障发生时，能否将其从其他故障中辨析和隔离出来。由文献[35]可知，在一个系统模型M中，若故障fi和fj满足式(4)的关系，则故障fi就能从故障fj中隔离出来。

式中：efi和 efj分别为含有故障 fi和 fj的方程；(M/{efj})+为消去方程efj的结构超定部分。

根据FI定义，可得到故障隔离矩阵(fault isolability matrix，FIM)，它可直观地反映出各故障的可隔离性。

由前面分析可知，增加位移传感器(ST1)能使所有故障可检测，图7(a)给出了此情况下的FIM矩阵，可知所有的故障不可隔离。

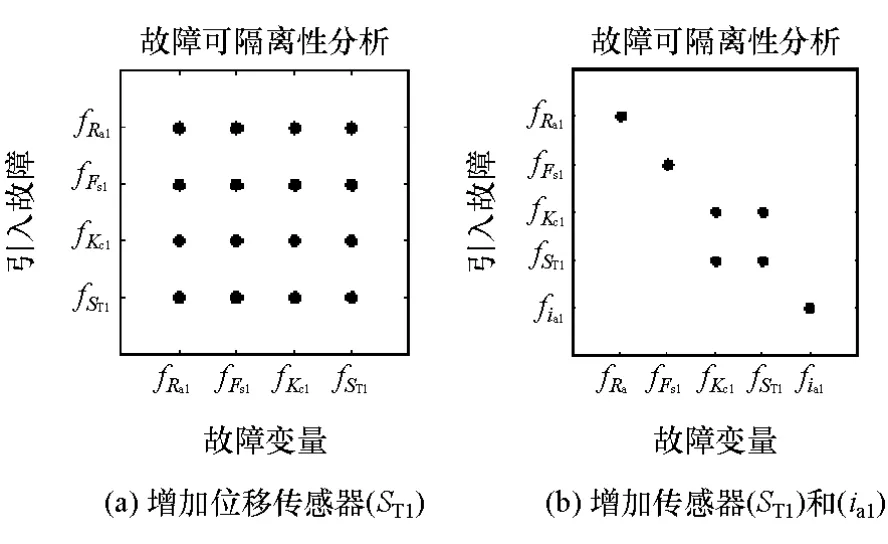
图7 不同传感器的故障隔离矩阵(FIM)

图7 中的“•”表示水平方向上的故障与竖直方向上故障之间的关联关系：若一个故障只与自身存在相关关系，此故障是可隔离的，如图7(b)中的故障fRa1，fFs1和fia1；若一个故障与其他故障存在相关关系，则故障是不可完全隔离的，如图7(b)中的故障fKC1和fST1。两者虽可从其他故障中隔离出来，但彼此不能互相隔离。

为使故障隔离性最大化，需要布置更多的传感器。经过分析，通过布置电流传感器(ia1)，可获得最大化的故障隔离性，其故障模型为

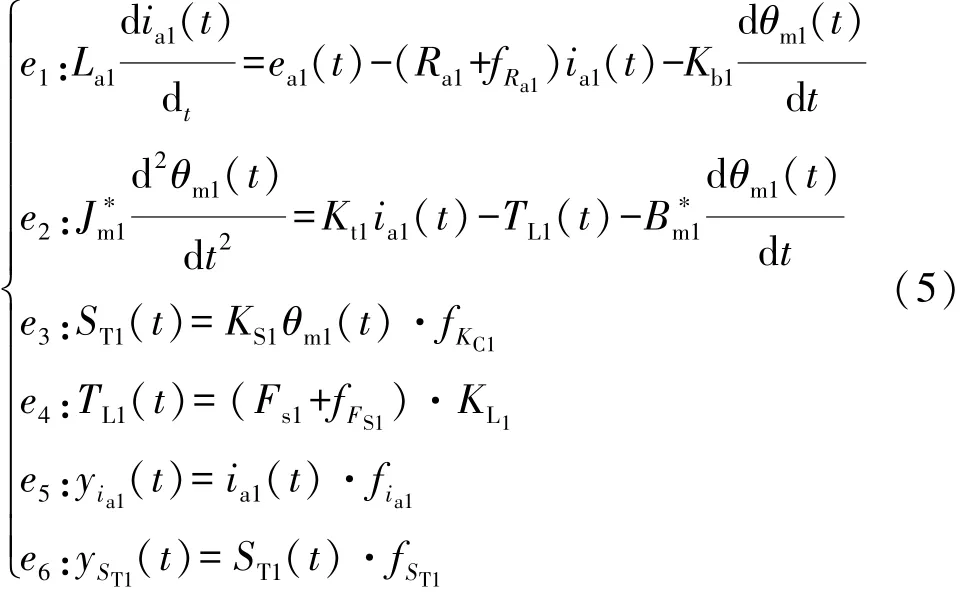
2.4 结构最小型超定方程集(MSO sets)

为了生成序列残差，用于FDI系统设计，首先要确定结构最小型超定方程集。利用文献[36]的理论，可获得4个结构最小型超定方程集，如表3所示。表中e1～e6为式(5)中的方程。

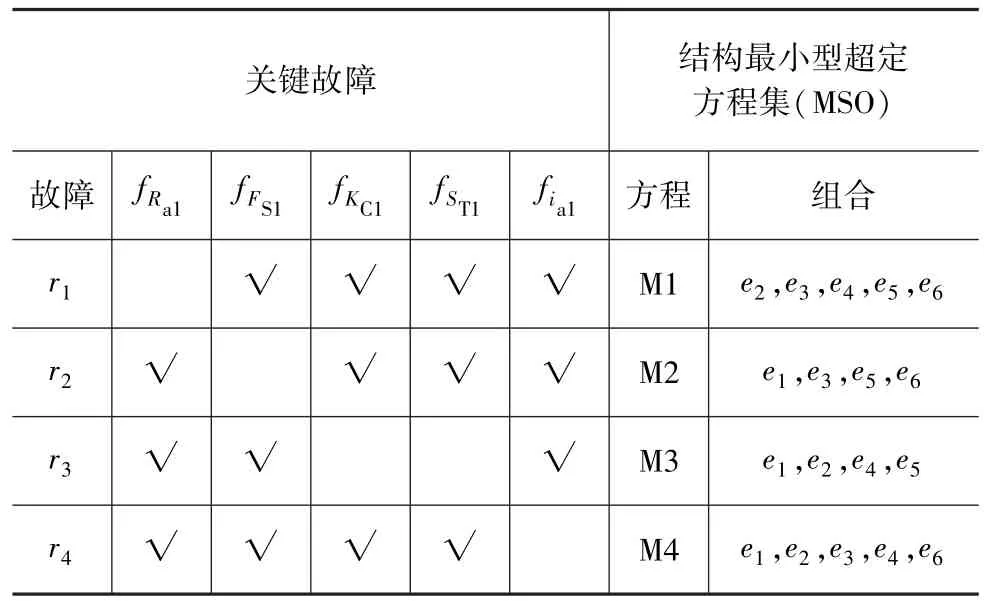
表3 结构最小型超定方程集和最小测试集

根据结构分析(SA)理论，上述结构最小型超定方程集可用于产生4个独立的残差，并可检测不同的故障，如表3所示。其中，符号“√”表示故障是可检测的，空白处表示故障不能检测。例如，残差r1能检测 4 个故障(fFS1，fKC1，fia1，fST1)，但是不能检测fRa1。

2.5 残差设计

2.5.1 残差r1

由表3可得，方程集 M1由 5个方程{e2，e3，e4，e5，e6}组成，用于产生残差r1。由于方程集M1仅有方程e2含有微分项，因此利用方程e2产生一个解析冗余关系(ARR)：

由文献[37]和文献[38]可知，解析冗余关系可用于产生残差，根据式(7)可计算出残差r1：

式中p为微分算子。根据控制理论，为了保证系统的稳定性，β＞0，且(p+β)的指数应不小于式(7)左边微分变量的最高阶数。

取状态变量即可获得残差r1的状态空间表示形式：

2.5.2 残差r2

由表3可得，方程集 M2由4个方程{e1，e3，e5，e6}组成，用于产生残差r2。利用产生残差r1相同的方法，即可得到一个解析冗余关系：

根据式(10)可计算出残差r2：

式中p为微分算子，β＞0可保证系统的稳定性。残差r2的状态空间表示形式为

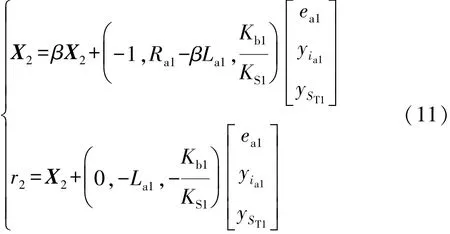
2.5.3 残差r3

由表3可得，方程集 M3由4个方程{e1，e2，e4，e5}组成，用于产生残差r3。由于方程集M3中e1和e2两个都含有微分项，不能直接采用基于ARR的残差设计方法，在此将采用标准的观察器方法来设计残差r3。 将e4代入e1和e2，M3变为

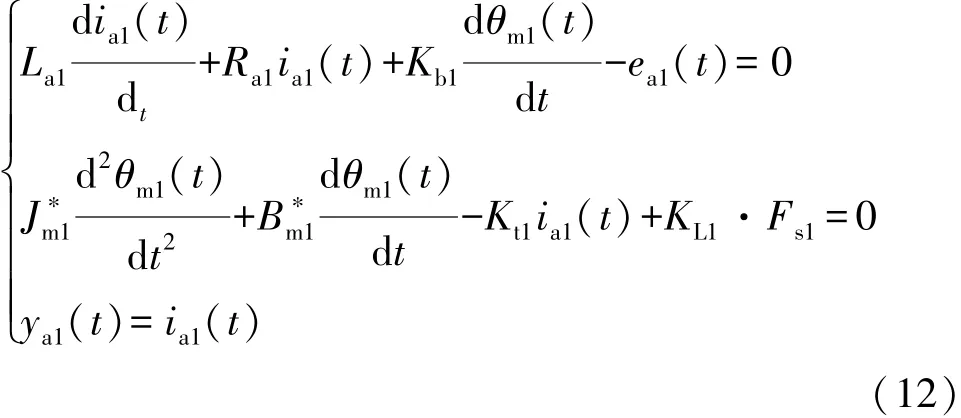
取状态变量X3＝(x1，x2)＝(ia1，θ.m1)，通过推导可获得残差r3的状态空间表示形式：

2.5.4 残差r4

由表3可得，方程集 M4由 5个方程{e1，e2，e3，e4，e6}组成，用于产生残差r4。利用产生残差r3相同的方法，即可获得残差r4。取状态变量x＝(x1，x2，x3)＝(ia1，θ.m1，θm1)，通过推导可获得残差r4的状态空间表示形式：

2.6 FDI系统仿真与校验

为了验证上述基于SA方法的故障可检测和可隔离分析结果的正确性，利用上述4个残差进行FDI系统设计，并对其进行模拟仿真与校验。图8给出了FDI系统模型原理图。

在MATLAB中建立换挡执行器的系统模型后，将系统模型中的相关信号引入到FDI系统中，并设置人为故障，检测FDI系统的有效性。图9显示无故障时，AMT某一路况下的换挡情况。

为了校验FDI系统，人为设置一系列故障，如表4所示，包括故障类型、发生时间和挡位状态。

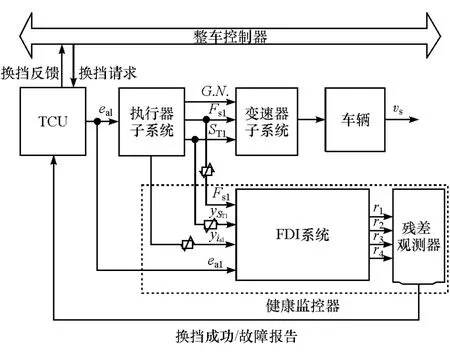
图8 FDI系统模型原理图

图9 无故障时换挡过程情况

表4 故障模拟

在人为设置故障后，对系统模型进行仿真，即可获得FDI系统中4个残差的信号输出情况，如图10～图13所示。为了快速评估FDI系统，选择固定值作为残差的阈值，通过判断残差的值是否超过对应的阈值，作为是否发生故障的判断条件。

图10 残差 r1 可检测故障 fFS1，fKC1，f ST1，fia1

图11 残差 r2 可检测故障 f Ra1，fKC1，f ST1，fia1

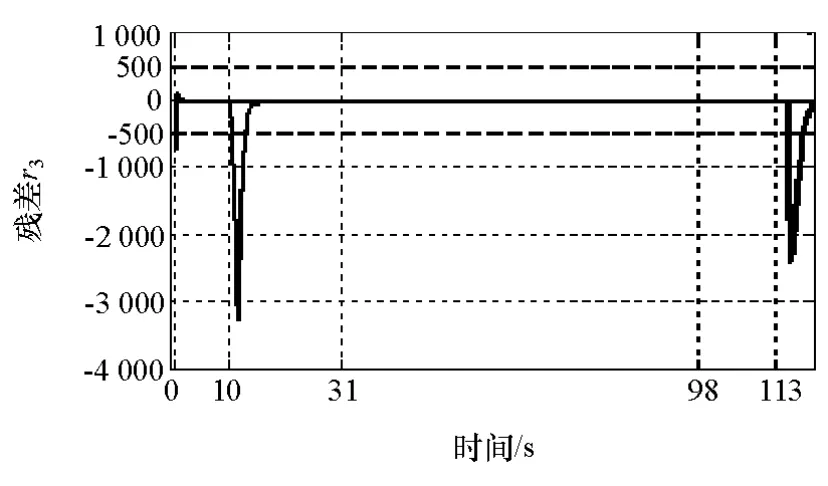
图12 残差r3可检测故障fRa1，f FS1，fia1

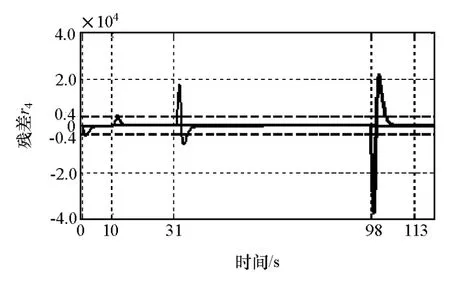
图13 残差 r4 可检测故障 f Ra1，fFS1，fKC1，f ST1

由图10可见，残差 r1在 10，31，98和 113s处可检测到故障，而在0处不能检测故障，即残差r1可检测故障 fFS1，fKC1，fST1，fia1，不能检测 fRa1；由图 11可见，残差r2在0，31，98和113s处可检测到故障，而在10s处不能检测故障，即残差r2可检测故障fRa1，fKC1，fST1，fia1，不能检测 fFS1；由图 12 可见，残差r3在0，10和113s处可检测到故障，而在31和98s处不能检测故障，即残差r3可检测故障 fRa1，fFS1，fia1，不能检测 fKC1，fST1；由图 13 可见，残差 r4在 0，10，31和98s处可检测到故障，而在113s处不能检测故障，即残差 r4可检测故障 fRa1，fFS1，fKC1，fST1，不能检测fia1。

表5显示了4个残差的故障检测结果。

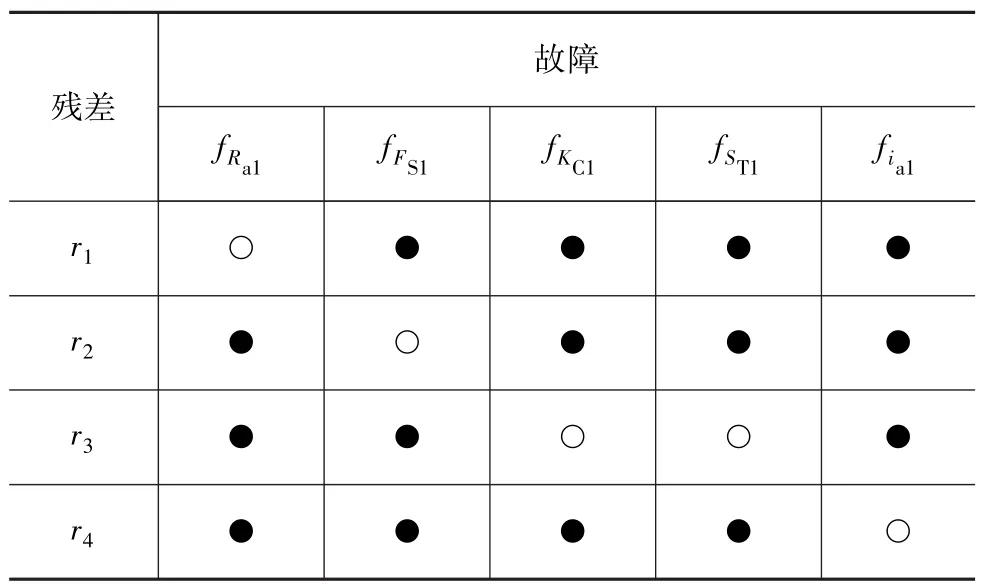
表5 4个残差的检测结果

由表5可见，FDI系统的故障检测结果与表3的分析结果一致，因此说明了基于SA的故障诊断方法有效、可行。

3 结论

(1)引入了结构分析法，阐述了其具体主要操作步骤，其中重要的4个方面为：故障模型的建立、DM分解、最小型超定方程集(MSO sets)的获取和序列残差的设计。

(2)应用了结构分析法故障诊断理论，进行AMT换挡执行器的故障诊断分析，获得了布置不同传感器的FD与FI能力对比；设计了AMT换挡执行器的故障检测与隔离(FDI)系统，通过仿真分析，对FDI系统进行了仿真和校验，证实了结构分析方法的有效性。

(3)完成了基于结构分析法的AMT换挡执行器故障诊断分析和仿真校验，结果表明：通过增加变速杆位移传感器和电流传感器，可实现故障可检测性与可隔离性能力最大化，即AMT线性执行器中的所有5个关键故障都可检测，其中有3个故障可完全隔离，另外2个故障可与其他3个故障隔离，但不能完全隔离。

[1] 陈玉东，施颂椒，翁正新.动态系统的故障诊断方法综述[J].化工自动化及仪表，2001，28(3)：1-14.

[2] FRANK P M.Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy：a survey and some new results[J].Automatica，1990，26(3)：459-474.

[3] 周东华，王桂增.故障诊断技术综述[J].化工自动化及仪表，1998，25(1)：58-62.

[4] MAÏGA M， RAMDANI N， TRAVÉ-MASSUYÈS L.Robust fault detection in hybrid systems using set-membership parameter estimation[J].IFAC-PapersOnLine，2015，48(21)：296-301.

[5] 康维国，蒋东翔.基于扩展卡尔曼滤波的燃气轮机性能参数估计与故障诊断[J].热能动力工程，2015，30(5)：702-707.

[6] 于劲松，沈琳，唐荻音，等.基于贝叶斯网络的故障诊断系统性能评价[J].北京航空航天大学学报，2016，42(1)：35-40.

[7] MEZIANE H，LABARRE C，LEFTERIU S，et al.Fault detection and isolation for a multi-cellular converter based on sliding mode observer[J].IFAC-PapersOnLine，2015，48(21)：164-170.

[8] BALLESTEROS-MONCADA H， HERRERA-LÓPEZ E J， ANZUREZ-MARÍN J.Fuzzy model-based observers for fault detection in CSTR[J].ISA Transactions，2015，59(325-333).

[9] LI L，DING S X，YANG Y，et al.Robust fuzzy observer-based fault detection for nonlinear systems with disturbances[J].Neurocomputing，2016，174：767-772.

[10] 朱纪洪，和阳，黄志毅.舵机特征模型及其故障检测方法[J].航空学报，2015，36(2)：640-650.

[11] 胡志坤，孙岩，姜斌，等.一种基于最优未知输入观测器的故障诊断方法[J].自动化学报，2013，39(8)：1225-1230.

[12] HWANG W，HUH K.Fault detection and estimation for electromechanical brake systems using parity space approach[J].Journal of Dynamic Systems Measurement＆ Control，2014，137(1)：1-7.

[13] PUIG V，BLESA J.Limnimeter and rain gauge FDI in sewer networks using an interval parity equations based detection approach and an enhanced isolation scheme[J].Control Engineering Practice，2013，21(2)：146-170.

[14] ZAKHAROV A， TIKKALA V M， JÄMSÄ-JOUNELA S L.Fault detection and diagnosis approach based on nonlinear parity equations and its application to leakages and blockages in the drying section of a board machine[J].Journal of Process Control，2013，23(9)：1380-193.

[15] 刘剑慰.基于模型的飞行控制系统故障诊断方法研究[D].南京：南京航空航天大学，2014.

[16] STAROSWIECKI M，DECLERCK P.Analytical redundancy in non linear interconnected systems by means of structural analysis[J].IFAC Proceedings Volumes，1989，22(6)：51-55.

[17] STAROSWIECKI M，DECLERCK P.Structural decomposition of large scale systems for the design of failure detection and isolation procedures[J].Systems Science，1994，20(1)：31-42.

[18] CASSAR J P，STAROSWIECKI M.A structural approach for the design of failure detection and identification systems[J].IFAC Proceedings Volumes，1997，30(6)：841-846.

[19] IZADI-ZAMANABADI R，STAROSWIECKIM.A structural analysis method formulation for fault-tolerant control system design[C].Decision and Control，2000.Proceedings of the 39th IEEE Conference on.IEEE，2000，5：4901-4902.

[20] KRYSANDER M，NYBERG M.Fault diagnosis utilizing structural analysis[R].CCSSE， Norrköping， Sweden，2002.

[21] KRYSANDER M，NYBERG M.Structural analysis for fault diagnosis of DAE systems utilizing MSS sets[J].IFAC Proceedings Volumes，2002，35(1)：143-148.

[22] FRISK E， DÜŞTEGÖR D， KRYSANDER M， et al.Improving fault isolability properties by structural analysis of faulty behavior models：application to the DAMADICS benchmark problem[J].IFAC Proceedings Volumes，2003，36(5)：1107-1112.

[23] DÜŞTEGÖR D， FRISK E， COCQUEMPOT V， et al.Structural analysis of fault isolability in the DAMADICS benchmark[J].Control Engineering Practice，2006，14(6)：597-608.

[24] KRYSANDER M， ÅSLUND J， NYBERG M.An efficient algorithm for finding minimal overconstrained subsystems for modelbased diagnosis[J].IEEE Transactions on Systems， Man， and Cybernetics-Part A： Systems and Humans，2008，38(1)：197-206.

[25] SVÄRD C， NYBERG M.Residual generators for fault diagnosis using computation sequences with mixed causality applied to automotive systems[J].IEEE Transactions on Systems Man and Cybernetics-Part A Systems and Humans，2010，40(6)：1310-1328.

[26] SVÄRDC，NYBERGM，FRISK E，et al.Automotive engine FDI by application of an automated model-based and data-driven design methodology[J].Control Engineering Practice， 2013， 21(4)：455-472.

[27] SUNDSTROM C，FRISK E，NIELSEN L.Selecting and utilizing sequential residual generators in FDI applied to hybrid vehicles[J].IEEE Transactions on Systems Man＆ Cybernetics：Systems，2014，44(2)：172-185.

[28] ZHANG J，RIZZONI G.Functional safety of electrified vehicles through model-based fault diagnosis[J].IFAC-PapersOnLine，2015，48(15)：454-461.

[29] CHEN Q，AHMED Q，RIZZONI G，et al.Design and evaluation of model-based health monitoring scheme for automated manual transmission[J].Journal of Dynamic Systems， Measurement， and Control，2016，138(10)：1-10.

[30] MAQUIN D，LUONG M，RAGOT J.Fault detection and isolation and sensor network design[J].Journal Européen Des Systèmes Automatisés，1997，31(2)：393-406.

[31] COMMAULT C，DION J M，SENAME O，et al.Observer-based fault detection and isolation for structured systems[J].IEEE Transactions on Automatic Control，2002，47(12)：2074-2079.

[32] CHEN Q，AHMED Q，RIZZONIG.Sensor placement analysis for fault detectability and isolability of an automated manual transmission[C].ASME 2014 Dynamic Systems and Control Conference.American Society of Mechanical Engineers，2014.

[33] SVARD C，NYBERG M.Residual generators for fault diagnosis using computation sequences with mixed causality applied to automotive systems[J].IEEE Transactions on Systems Man and Cybernetics-Part A Systems and Humans，2010，40(6)：1310-1328.

[34] DULMAGE A L，MENDELSOHN N S.Coverings of bipartite graphs[J].Canadian Journal of Mathematics，1958，10(517-534).

[35] KRYSANDER M，FRISK E.Sensor placement for fault diagnosis[J].IEEE Transactions on Systems Man and Cybernetics Part A：Systems ＆ Humans，2008，38(6)：1398-1410.

[36] KRYSANDER M，NYBERG M.An efficient algorithm for finding over-constrained subsystems for construction of diagnostic tests[C].16th International Workshop on Principles of Diagnosis DX-05，2005.

[37] FRISK E，NYBERG M.A minimal polynomial basis solution to residual generation for fault diagnosis in linear systems[J].Automatica，2001，37(9)：1417-1424.

[38] NYBERG M，FRISK E.Residual generation for fault diagnosis of systems described by linear differential-algebraic equations[J].IEEE Transactions on Automatic Control，2006，51(12)：1995-2000.

A Research on Structural Analysis-based Fault Diagnosis Theory and Its Application

Chen Qi1， Yao Zhigang1， Qadeer Ahmed2， Zhang Zhen1＆ He Liangguo1

1.School of Mechanical Engineering， Hefei University of Technology， Hefei 230009；2.Center of Automotive Research， The Ohio State University， Columbus， USA 43212

In order to maximize the fault diagnosis capability of system and rapidly design fault diagnosis system，the theory of fault diagnosis based on structural analysis(SA)is applied.Its main procedures are as follows： firstly， the key faults of system are detected by the techniques of failure modes and effects analysis(FMEA)with its fault model established.Secondly，the fault detectability(FD)and fault isolability(FI)of system are evaluated by using Dulmage-Mendelsohn(DM)decomposition and fault isolation matrix(FIM)analysis.Thirdly，combined with minimal structurally over-determined(MSO)sets，the residual design of system is fulfilled based on analytical redundant relation(ARR)and observer-based parameter evaluation techniques.Finally，with the shifting actuator of an automated mechanical transmission(AMT)as an example，an analysis on its fault diagnosis ability and the design of fault detection and isolation(FDI)system are conducted by using SA technique，and a simulation is performed on FDI system with MATLAB/Simulink and the effectiveness of the method adopted is validated.

AMT shifting actuator； fault diagnosis； structural analysis； Dulmage-Mendelsohn decomposition；fault isolability matrix analysis

10.19562/j.chinasae.qcgc.2017.11.018

∗国家自然科学基金(51675151和51405127)资助。

原稿收到日期为2016年12月1日，修改稿收到日期为2017年7月17日。

陈奇，副教授，E-mail：sencq＠ 163.com。