裂项相消法在数列求和中的妙用

■河南省郑州市第一中学1903班 孙静楠

裂项相消法在数列求和中的妙用

■河南省郑州市第一中学1903班 孙静楠

众所周知,若数列{an}为等差数列,数列{bn}为等比数列,cn=anbn,求数列{cn}的前n项和时常用错位相减法。但错位相减法运算复杂,结果不易算对或不易化为最简形式,为此,我们借助例题介绍用裂项相消法求这类数列的前n项和。

分析：要想用裂项相消法求数列{an}的前n项和Sn,首先应把an=(3n-1)×4n分解为另一数列相邻两项差的形式,即构造新数列{bn},使an=bn+1-bn,从而利用Sn=a1+a2+a3+…+an=(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)=bn+1-b1。

构造数列{bn}可用待定系数法实现。

解：不设an=(3n-1)×4n=[λ(n+1)+μ]×4n+1-(λn+μ)×4n=(3λn+4λ+3μ)×4n。

同样,利用裂项相消也可以解决等比数列求和问题。

解：设an=a1qn-1=kqn-kqn-1=k(q-1)qn-1。令k(q-1)=a1,得

所以等比数列{an}的前n项和:

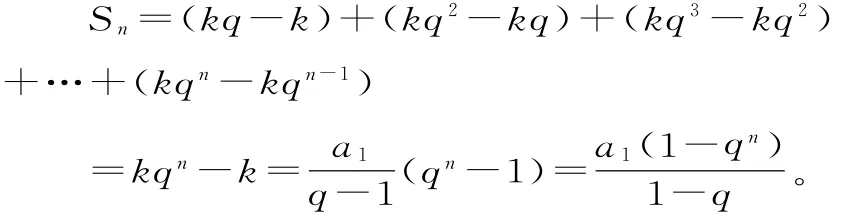
推广:若数列{an}的通项公式为关于n的多项式,数列{bn}为等比数列,cn=anbn的前n项和的求解也可用裂项相消法。

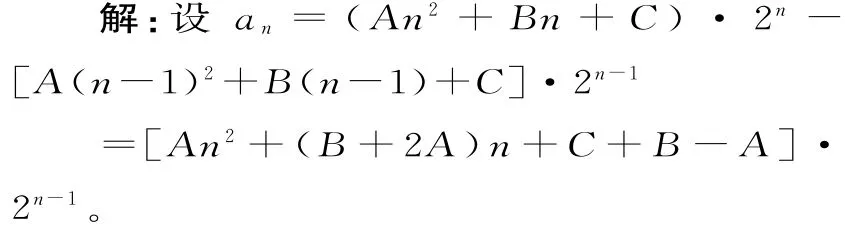
比较系数可得A=2,B+2A=0,C+B-A=0,从而A=2,B=-4,C=6。

令bn=[A(n-1)2+B(n-1)+C]·2n-1=[2(n-1)2-4(n-1)+6]·2n-1=[(n-1)2-2(n-1)+3]·2n。

所以Sn=a1+a2+a3+…+an=(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)=bn+1-b1=(n2-2n+3)·2n+1-6。

从以上例题可以看出,借助待定系数法,把cn=anbn型数列(其中数列{an}的通项公式为关于n的多项式,数列{bn}为等比数列)裂项相消求和,可使计算简单,过程简洁,结果规范,大大降低了计算失误的可能。

(责任编辑 徐利杰)