化归转化思想在正、余弦定理中的应用

■重庆市育才中学 何宜珂

化归转化思想在正、余弦定理中的应用

■重庆市育才中学 何宜珂

化归与转化思想,就是紧扣求解目标,通过数学内部的联系,在转化中实现问题的规范化,即运用有关的数学方法,将待解决的问题逐步转化为简单的、熟悉的或已经解决了的问题去解决。正弦定理、余弦定理沟通了三角形中边与角的关系,用这两个定理可以实现边与角的转化,从而简化解题过程,下面举例说明。

一、繁杂转化为简单

对于很多数学问题,通过同解变形,将繁杂的问题转化成特殊的、简单的问题,解决起来就容易得多了。

分析：由正弦定理得c=2RsinC,a=2RsinA,b=2RsinB,其中R为△ABC外接圆半径。由余弦定理得c2=a2+b2-2abcosC,可得余弦定理的变形形式:sin2C=sin2A+sin2B-2sinAsinBcosC。

证明：sin2A+sin2B+cos2C+2sinA·sinBcos(A+B)=sin2A+sin2B-2sinA·sinBcosC+cos2C=sin2C+cos2C=1。

二、陌生转化为熟悉

各类数学问题组成数学问题的海洋,每一个数学问题就是题海中的一滴水。对我们每个人来说,没见过、没练过的数学问题要比见过、练过的多得多。所以我们只有将陌生问题转化为熟悉问题,才容易找到切入点。

证明：由sin2A-cos2得cos2A=又A是三角形的内角,则得

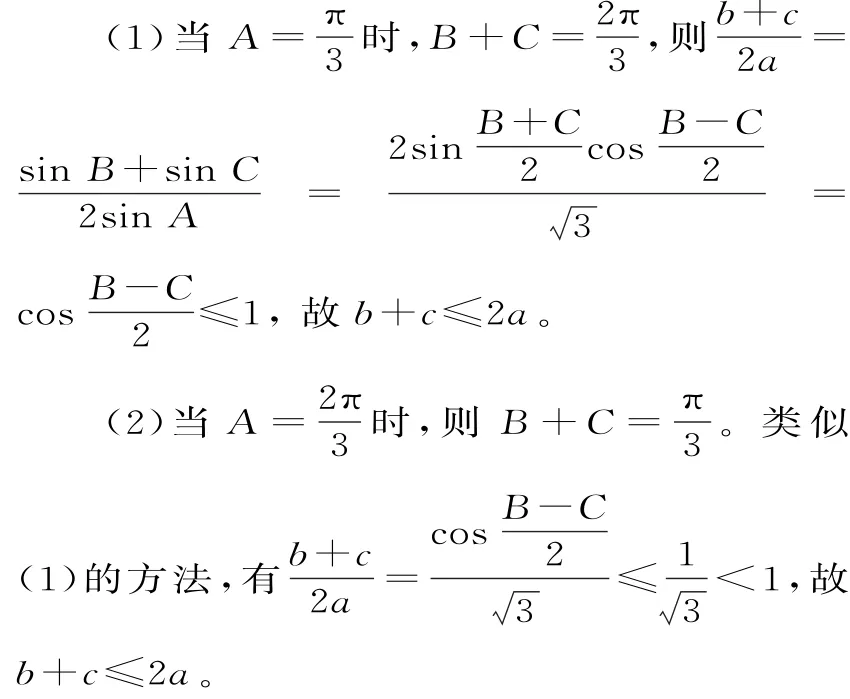
综上,恒有b+c≤2a。

三、数式转化为图形

有些代数问题直接用代数方法解决起来比较困难,可以转化为几何图形,借助图形特点来解决。

分析：在△ABC中,由正弦定理得c=2RsinC,a=2RsinA,b=2RsinB,其中R为△ABC外接圆半径。由余弦定理得c2=a2+b2-2abcosC,于是可得余弦定理的变形形式:sin2C=sin2A+sin2B-2sinA·sinBcosC。

解：如图1所示,构造△ABC,设外接圆半径为1,∠A=20°,∠B=40°,∠C=120°,则:

原式=sin220°+sin240°+sin20°sin40°

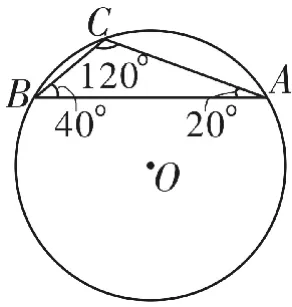
图1

=sin220°+sin240°-2sin20°sin40°cos120°=sin2A+sin2B-2sinAsinBcosC=sin2C=sin2120°=

小结：在化归转化的过程中,一定要注意转化的等价性。若实施了不等价转化,解后应检验其结果,否则极易出错。

(责任编辑 徐利杰)