基本不等式的应用

■江苏省张家港市第二中学 何海虹

基本不等式的应用

■江苏省张家港市第二中学 何海虹

基本不等式及其应用作为高考中的一个考点,在高考中有时单独考查,有时与其他知识加以交汇,主要出现在与不等式的基本性质的交汇、最值问题的求解、逻辑问题的判定以及实际应用问题的判定等方面。解这些问题时,我们要注意:(1)基本不等式成立的条件的确定;(2)等号成立往往是最值确定的关系,要注意参数值的取值;(3)正确合理的变形往往是利用基本不等式的前提条件。

一、求解最值问题

方法链接：基本不等式是求函数最值的有力工具,在使用基本不等式求函数最值时,要注意应用条件“一正、二定、三相等”。不要仅仅关注结构上的定值,而忽略对相等条件的考察。(2017·山东文·12)若直线+=1(a＞0,b＞0)过点(1,2),则2a+b的最小值为____。

分析：根据直线过点的条件确定定值问题,利用基本不等式加以变形与综合,最后求解相应的最值问题。

故答案为8。

点评:本题主要考查化归与转化思想。在利用基本不等式求最值时,常用的技巧就是“1”的代换,其目的就是借助“1”将所求式子的结构进行调整,直至优化到能够利用基本不等式为止。

二、求解参数值问题

方法链接：求解参数值问题时,往往结合已知不等式,利用不等式等号成立的条件来求解相应的参数值问题。解决问题时,往往先通过猜测确定参数值,再利用基本不等式来证明。

分析：由于已知不等式是关于正实数a,b,c的轮换对称式,这表明这三个字母在不等式中的地位相同,因此当a=b=c时不等式的等号成立。对于这个不等式等号成立的条件,可结合已知利用配凑构造基本不等式来求解。

解：当a=b=c=1时,代入已知不等式ab+bc+ca+k 2,那么最小的正实数k=2。

点评:本题主要考查基本不等式,考查转化与化归思想。解决参数值的求解问题,往往是通过基本不等式的条件“三相等”来加以转化,进而确定参数值。

三、处理恒成立问题

方法链接：求解含参数的不等式恒成立问题,可通过分离参数把参数的范围化归为函数的最值问题。a＞f(x)恒成立⇔a＞[f(x)]max,a＜f(x)恒成立⇔a＜[f(x)]min。

A.(-∞,-1)

B.(-∞,22-1)

C.(-1,22-1)

D.(-22-1,22-1)

分析：将函数恒为正值转化为参数恒成立问题,根据指数函数的性质和基本不等式的解法即可求解参数k的取值范围。

解：由f(x)＞0得32x-(k+1)·3x+

所以k+1＜22,解得k＜22-1,故答案为B。

点评:求解不等式恒成立问题,经常采用参数分离法,这是解决此类问题的关键。同时还要注意利用基本不等式的条件及基本初等函数的基本性质与应用等。

四、证明不等式问题

方法链接：证明不等式时应根据求证式两端的结构,合理选择重要不等式及其变形不等式。

分析：根据两代数式均为正的条件,利用基本不等式的变式加以转化,可以证明所要求证的不等式成立。

证明：因为a＞2,所以loga(a-1)＞0,loga(a+1)＞0。

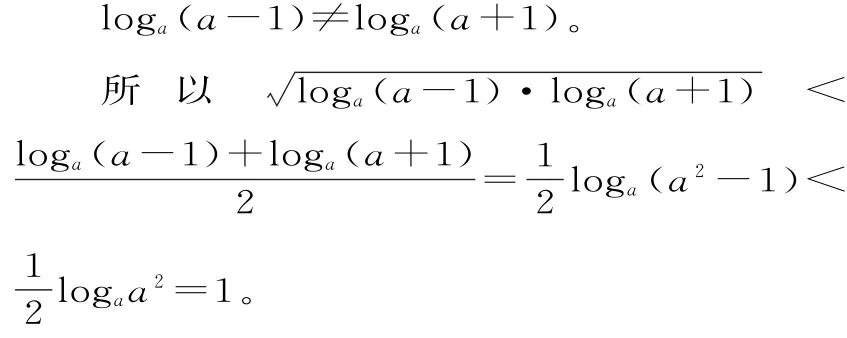
所以loga(a-1)loga(a+1)＜1。

点评:在利用基本不等式证明相应的不等式问题时,往往所给不等式的结构与基本不等式的结构特点有较大的差异,所以常常要使用一定的变形技巧与转化策略,对原不等式的结构进行适当的改造才能应用。

五、求解方程问题

方法链接：应用基本不等式解决实际问题时,应注意把要求最值的变量设为函数。列函数解析式时,要注意所设变量的范围。

分析：由于方程的左边的未知数x的次数是偶次的,右边是奇次的,则可判断方程的解x≥0,又x=0代入方程不成立,那么方程的解肯定是正数,通过方程两边同时除以x2017,结合等式的展开并利用基本不等式来处理即可达到求解方程的目的。

解：由于方程的左边的未知数x的次数是偶次的,右边是奇次的,则可判断方程的解x≥0,又x=0代入方程不成立,那么方程的解x＞0。

故原方程的解为x=1。

点评:本题主要考查方程的求解和基本不等式的应用。直接求解方程显然无法下手,而通过方程的转化,结合关系式的展开,利用基本不等式,结合不等式与方程的关系则容易求解。

(责任编辑 赵 平)