利用基本不等式破解最值问题

■江西省瑞金市第三中学 刘小东

利用基本不等式破解最值问题

■江西省瑞金市第三中学 刘小东

利用基本不等式求最值时,必须注意“一正,二定,三相等”。①一正:关系式中,各项均为正数;②二定:关系式中,含变量的各项的和或积必须有一个为定值;③三相等:含变量的各项均相等。要取得最值,三条件缺一不可。如果项是负数,可转化为正数后解决,当和(或积)不是定值时,需要对项进行添加、分拆或变系数,将和(或积)化为定值。

题型一：已知x＞0,求x+k(k＞0)的x最小值,可直接利用基本不等式。

解析：因为a,b∈R,ab＞0,则a4+4b4≥4a2b2。

评注:本题先利用重要不等式得出a4+4b4≥4a2b2,再利用基本不等式得出≥4,取等号的条件由前后共同决定。

评注:本题属于基本不等式在应用题中的运用。题型二：已知正数x,y满足m(λ,μ∈R+,m∈R+且m为定值),求px+qy(p,q∈R+)的最小值。

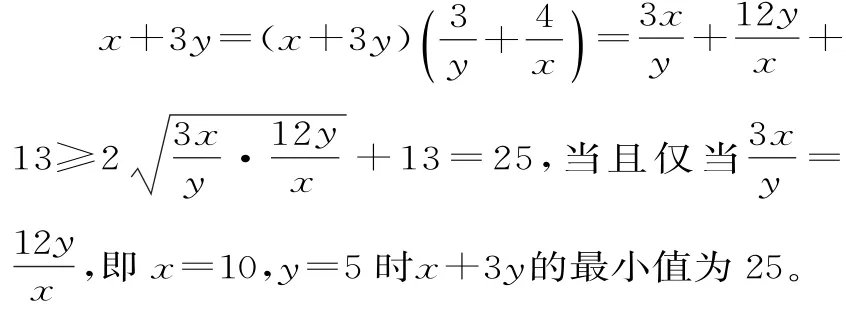
评注:本题主要考查基本不等式。先将已知式子变形,再利用1的灵活应用,给待求式子配上式子,再运用基本不等式和不等式性质求出最值。

A.8 B.9 C.12 D.16

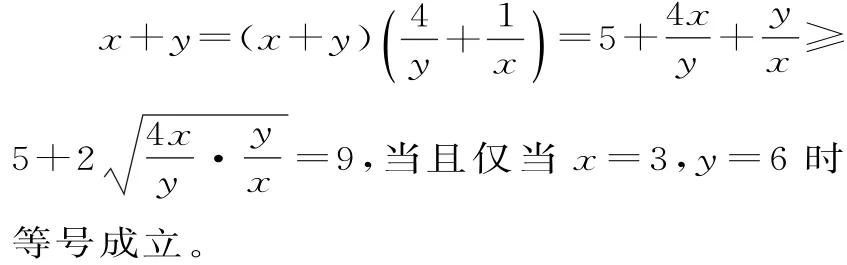
综上可得x+y的最小值为9。故应选B。

评注:本题中给定的形式不直接适合基本不等式,可将已知式子变形,给待求式子配上式子,构造出基本不等式的形式再进行求解。

题型三：已知正数x,y满足λx+μy=

m(λ,μ∈R+,m∈R+且m为定值),求的最小值。

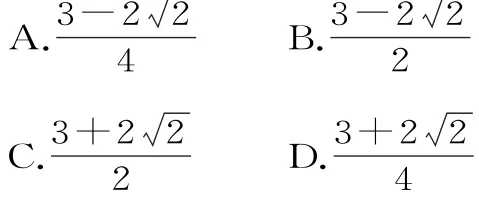
解析：直线平分圆周,则直线过圆心(1,1),所以有a+b=2(当且仅当b=2a时取“=”),故应选D。

评注:本题先利用直线与圆的位置关系列出式子,再运用基本不等式求解。

评注:对于本题,给已知式子配上式子x+(1-x),再利用多项式的乘法相乘,分组并项后利用基本不等式即可求出最小值。

题型四：利用基本不等式将等式放缩,得到不等式,再求解。

评注:在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误。本题中利用基本不等式,将等式转化为不等式,再解一元二次不等式,结合已知条件,得出mn的最小值。

(责任编辑 徐利杰)