数列必考类型总结

■河南师范大学附属中学 孟召臣

数列必考类型总结

■河南师范大学附属中学 孟召臣

类型一:基本量的运算

等差(等比)数列均有首项a1、公差d(公比q)、某项an、项数n、前n项和Sn这5个基本量,只要知道其中任意三个基本量,就可以求出另外两个基本量。

1.等差数列基本量的运算

(1)(2015年新课标全国Ⅰ卷)已知{an}为公差为1的等差数列,Sn为{an}的前n项和,若S8=4S4,则a10=____

(2)已知等差数列{an},它的前5项的和为34,最后5项的和为146,所有项的和为234,则a7=____

解析:(1)由{an}的公差为1,S8=4S4⇒8a1+28=4(4a1+6)⇒a1=

(2)设数列{an}首项为a1,末项为an,公差为d,则依题意得:

结合题意知Sn==18n=234,解得n=13。从而有a1+a13=36,a7=

2.等比数列基本量的运算

(1)设等比数列{an}的前n项和为Sn,若a1=1,S6=4S3,则a4=____。

(2)已知等比数列{an}的首项a1=1,公比q≠1,且a2,a1,a3成等差数列,则其前5项和S5=____。

解析:(1)设等比数列{an}的公比为q(q≠1),根据题意知a1=1,S6=4S3,即:1+q3=4⇒q3=3⇒a4=a1q3=3。

(2)由a1=1,a2,a1,a3成等差数列可得q+q2=2⇒q=-2或q=1(舍去)。

故S5==11。

类型二:等差、等比数列性质的应用

1.等差数列的性质

(1)等差数列{an}中,a9=+6,则数列{an}的前11项和S11=

(2)设Sn是等差数列{an}的前n项和,

(3)等差数列{an}中总项数为奇数,且此数列中的奇数项之和为77,偶数项之和为66,a1=1,求其项数和中间项。

(4)已知Sn为等差数列{an}的前n项和,若a1＞0,S9=S17,则数列{an}的前多少项和最大?

解析:(1)a9=a12+6⇒a6=2a9-a12=12⇒S11=11a6=132。

(3)设数列的项数为2n+1项,则:S奇=77,S偶=

(4)据题意S9=S17可得:

a10+a11+…+a17=0。

而a10+a17=a11+a16=a12+a15=a13+a14,故a13+a14=0。

结合a1＞0,可得a13＞0,a14＜0,所以数列{an}的前13项和最大。

2.等比数列的性质

(1)在等比数列{an}中,则a3·a13的值等于____。

(2)已知数列{an}为递增的等比数列,a1+a4=9,a2a3=8,则数列{an}的前n项和为

(3)已知数列{an}是等比数列,若Sm=48,S2m=60,则S3m=____。

解析:(1)a1·a15=a4·a12⇒

(2)因为a1+a4=9,a1a4=a2a3=8,所以a1=1,a4=8或a1=8,a4=1(舍去)。

(3)解法一:因为Sm=48≠0,所以Sm,S2m-Sm,S3m-S2m仍成等比数列。

故(60-48)2=48·(S3m-60),解得S3m=63。

解法二:因为S2m=Sm+qmSm,所以60=48+48qm,解得qm=

故S3m=Sm+qmS2m=48+×60=63。

解法三:不妨令m=1,则Sm=S1=a1=48,S2m=S2=a1+a2=60。

故a2=12,q=,a3=a2q=3。

所以S3m=S3=S2+a3=63。

类型三:递推数列

1.形如an+1-an=f(n)型

此种类型,通常f(n)为关于n的函数,求解常用累加法。一般解法如下:

n≥2时,an-an-1=f(n-1)。

故an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=f(n-1)+f(n-2)+…+f(2)+f(1)+a1。

(1)已知数列{an}满足an+1=an+2n+1,a1=1,求数列{an}的通项公式。

(2)已知数列{an}满足an+1=3an+2·3n+1,a1=3,求数列{an}的通项公式。

解析:(1)由an+1=an+2n+1,得an+1-an=2n+1。

故an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+(a2-a1)+a1

=[2(n-1)+1]+[2(n-2)+1]+…+(2×2+1)+(2×1+1)+1

=2[(n-1)+(n-2)+…+2+1]+n

所以数列{an}的通项公式为an=n2。

(2)an+1=3an+2·3n+1,两边同时除以3n+1,得

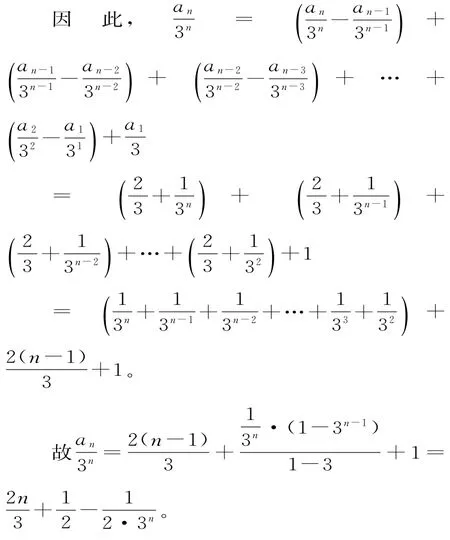
则an=2n·3n-1+

点评:第二小题的关键是把递推关系式an+1=3an+2·3n+1转化为进而求出即得数列的通项公式,最后再求数列{an}的通项公式。

2.形如an+1=can+d(c≠0,其中a1=a)型

通常c≠1且d≠0时,数列{an}为线性递推数列,其通项通常有以下两种解法。

思路一:设an+1+λ=c(an+λ),得an+1=can+(c-1)λ,与题设an+1=can+d比较系数得(c-1)λ=d,所以λ=(c≠1)。所以有

思路二:从递推关系an+1=can+d中把n换成n-1有an=can-1+d,两式相减得an+1-an=c(an-an-1),从而化为公比为c的等比数列{an+1-an}。

进而求得an+1-an=cn(a2-a1),再通过累加求得通项公式。

已知数列{an}中,a1=2,an+1=求通项an。

解法一:由an+1=得an+1-1所以数列{an-1}是以a1-1=1为首项,为公比的等比数列,an-1=即

解法二:a1=2,且则a2时

上面两式相减得an+1-an=(anan-1),故数列{an+1-an}是以a2-a1=-为首项,以为公比的等比数列。

an+1-an=-

故an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1

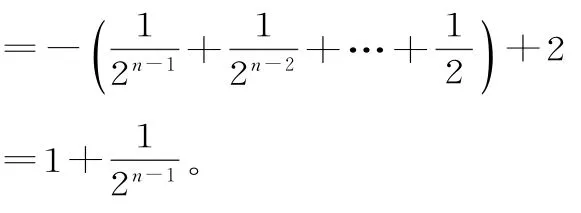
类型四:数列求和

1.利用公式求和

等比数列求和公式,Sn=

常见的三个求和公式也需记住:

求-12+22-32+42-52+62-…-992+1002的和。

解析:-12+22-32+42-52+62-…-992+1002

=(22-12)+(42-32)+(62-52)+…+(1002-992)

=(2-1)(2+1)+(4-3)(4+3)+(6-5)(6+5)+…+(100-99)(100+99)

=3+7+11+…+199。

由等差数列的求和公式得S50=

2.分组求和

一个数列的通项公式是由若干个等差、等比或其他可求和的数列组成,求和时可用分组求和法,分别求和后再相加减。

解析:

(责任编辑 徐利杰)