数列综合拔高训练（B卷）

■郑州外国语学校 邱培云

数列综合拔高训练（B卷）

■郑州外国语学校 邱培云

一、选择题(本大题共31个小题。)

1.已知数列{an}是等差数列,且a7-2a4=6,a3=2,则公差d=( )。

A.8 B.9 C.10 D.11

3.在等差数列{an}中,若a4+a6+a8+a10+a12=120,则的值为( )。

A.14 B.15 C.16 D.17

4.已知函数f(x)=-log2x,正实数a,b,c是公差为正数的等差数列,且满足f(a)·f(b)f(c)＜0。若实数d是方程f(x)=0的一个解,那么下列四个判断“①d＜a;②d＜b;③d＜c;④d＞c”中,有可能成立的个数为( )。

A.1 B.2 C.3 D.4

5.在等差数列{an}中,a3+a6+a9=27,设数列{an}的前n项和为Sn,则S11=( )。

A.18 B.99 C.198 D.297

6.如果a1,a2,…,a8为各项都大于零的等差数列,公差d≠0,则( )。

A.a1a8＞a4a5B.a1a8＜a4a5

C.a1+a8＞a4+a5D.a1a8=a4a5

7.已知等差数列{an}前9项的和为27,a10=8,则a100=( )。

A.100 B.99 C.98 D.97

8.若方程x2-2x+m=0和x2-2x+n=0的四个根组成一个首项为的等差数列,则|m-n|=( )。

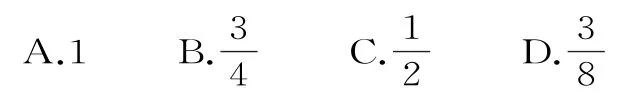
9.公差不为零的等差数列{an},其前n项和为Sn,若a4=2(a2+a3),则等于( )。

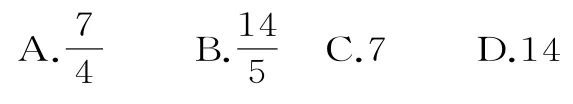
10.已知两个等差数列{an}和{bn}的前n项和分别为An和Bn,且则使得为整数的正整数n的个数是( )。

A.2 B.3 C.4 D.5

11.明朝数学家程大位的《算法统宗》中有首依等算钞歌:“甲乙丙丁戊己庚,七人钱本不均分,甲乙念三七钱钞,念六一钱戊己庚,惟有丙丁钱无数,要依等第数分明,请问先生能算者,细推详算莫差争。”大意是:“现有甲、乙、丙、丁、戊、己、庚七人,他们手里的钱不一样多,依次成等差数列,已知甲、乙两人共237钱,戊、己、庚三人共261钱,求各人钱数。”根据题目的已知条件,丙有( )。

A.100钱 B.101钱

C.107钱 D.108钱

12.已知等差数列{an}一共有12项,其中奇数项之和为10,偶数项之和为22,则公差为( )。

A.1 B.2 C.5 D.12

13.已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的斜率是( )。

A.4 B.3 C.2 D.1

14.在数列{an}中,若a1=2,且对任意正整数m,k,总有am+k=am+ak,则{an}的前n项和Sn=( )。

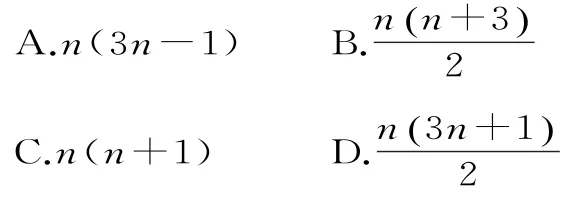
15.已知数列{an}的前n项和为Sn=n2-n,令bn=ancos记数列{bn}的前n项为Tn,则T2015=( )。

A.-2014 B.-2013

C.-2012 D.-2011

16.数列{an}中,an+1+(-1)nan=2n-1,则数列{an}的前12项的和等于( )。

A.76 B.78 C.80 D.82

17.已知无穷数列{an}和{bn}都是等差数列,其公差分别为k和h,若数列{anbn} 也是等差数列,则( )。

A.h2+k2=0

B.hk=0

C.h,k可以是任何实数

D.不存在满足条件的实数h和k

18.若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则m的取值范围是( )。

A.(1,2) B.(2,+∞)

C.[3,+∞) D.(3,+∞)

19.已知等差数列{an}的前n项和为Sn,若数列{Sn}有唯一的最大项S3,Hn=S1+2S2+3S3+…+nSn,则( )。

A.S5·S6＜0

B.H5·H6＜0

C.数列{an},{Sn}都是单调递减数列

D.H6可能是数列{Hn}中的最大项

20.已知数列{an}满足an+2-an+1=an+1-an(n∈N*),且a5=若函数f(x)=sin2x+2cos2记yn=f(an),则数列{yn}的前9项和为( )。

A.-9 B.0 C.1 D.9

21.若数列{an}是公比为4的等比数列,且a1=4,则数列{log2an}是( )。

A.公比为lg2的等比数列

B.公差为lg2的等差数列

C.公比为2的等比数列

D.公差为2的等差数列

22.已知等差数列{an}的前n项和为Sn,且满足2S3-3S2=6,则数列{an}的公差是( )。

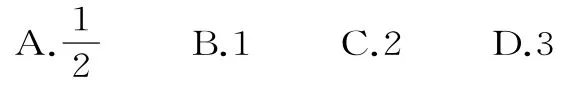
23.已知数列{an}的前n项和为Sn,且Sn=2(an-1),则a5=( )。

A.16 B.32 C.64 D.128

24.已知等差数列1,a,b,等比数列3,a+2,b+5,则a+b的值为( )。

A.-11或7 B.11或-7

C.11 D.-7

25.已知等比数列{an}的公比为正数,且a4·a10=2a26,a3=1,则a6=( )。

A.1 B.22 C.2 D.4

26.已知等差数列{an}前n项的和为Sn,则a1=( )。

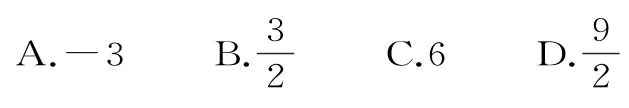
27.已知等差数列{an}中,a3,a15是方程x2-6x-1=0的两根,则a7+a8+a9+a10+a11等于( )。

A.18 B.-18 C.15 D.12

28.若a,b是函数fx()=x2-px+q p＞0,q＞0()的两个不同的零点,且a,b,-2这三个数适当排序后可成等差数列,也可适当排序后成等比数列,则p+q的值等于( )。

A.6 B.7 C.8 D.9

29.已知各项不为0的等差数列{an},满足a3-+a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=( )。

A.2 B.4 C.8 D.16

30.已知等比数列的首项为8,Sn是其前n项的和,某同学计算得到S2=20,S3=36,S4=65,后来该同学发现其中一个数算错了,则该数为( )。

A.S1B.S2C.S3D.S4

31.设a1,a2,…,an(n≥4)是各项均不为零的等差数列,且公差d≠0。设f(n)是将此数列删去某一项得到的数列(按原来的顺序)为等比数列的最大的n值,则f(n)=( )。

A.4 B.5 C.6 D.7

二、填空题(本大题共17个小题。)

32.设Sn为等差数列{an}的前n项和,S2=S6,a4=1,则a5=____。

33.已知等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为____。

34.已知数列{an}的前n项和为Sn,a1=1,an≠0,anan+1=4Sn-1(n∈N*),则数列{an}的通项公式为____。

35.设等差数列{an}的前n项和为Sn,若S3=2a3,S5=15,则a2016=____。

36.在等差数列{an}中,若S9=18,Sn=240,an-4=30,则n的值为____。

37.已知等差数列{an}的公差d≠0,且若a1=1,Sn为数列{an}的前n项和,则的最小值为____。

38.设Sn是数列{an}的前n项和,且a1=-1,an+1=SnSn+1,则Sn=____。

39.已知等差数列{an}的前n项和为Sn,若(a2-1)3+2010(a2-1)=1,(a2009-1)3+2010(a2009-1)=-1,则下列四个结论中正确的序号为____。

①S2009=2009;②S2010=2010;③a2009＜a2;④S2009＜S2。

40.数列{an}满足=d(n∈N*,d为常数),则称数列{an}为调和数列,记数列为调和数列,且x1+x2+…+x20=200,则x5+x16=____。

41.正项数列{an}满足:a1=2,a2=1,且则此数列的第2017项为____。

42.已知数列{an}的通项为an=其前n项和为Sn,则S30=____。

43.已知数列{an}是各项均不为零的等差数列,Sn为其前n项和,且若不等式对任意n∈N*恒成立,则实数λ的最大值为____。

44.数列{an}满足a1=1,记Sn=若S2n+1对任意n∈N*恒成立,则正整数t的最小值为____。

45.已知数列{an}满足a1=an+1=若0恒成立,则实数t的取值范围是____。

46.在由正数组成的等比数列{an}中,a1+a2=4,a3+a4=1,则a5+a6=

47.设等比数列{an}的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为____。

48.已知数列{an}是递增的等比数列,a1+a4=9,a2a3=8,则数列{an}的前n项和等于____。

三、解答题(本大题共11个小题。)

49.已知等差数列{an}的前n项和为Sn,且a3+a6=4,S5=-5。

(1)求数列{an}的通项公式;

(2)若Tn=|a1|+|a2|+|a3|+…+|an|,求T5的值和Tn的表达式。

50.数列{an}满足a1=1,a2=2,an+2=2an+1-an+2。

(1)假设bn=an+1-an,试证明{bn}是等差数列;

(2)求{an}的通项公式。

51.已知等差数列{an}的公差d＞0,设{an}的前n项和为Sn,a1=1,S2·S3=36。

(1)求d及Sn;

(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65。

52.已知数列{an}的前n项和为Sn,a1=1,an≠0,anan+1=λSn-1,其中λ为常数。

(1)证明:an+2-an=λ;

(2)是否存在λ,使得{an}为等差数列?并说明理由。

53.已知数列{an},an＞0,其前n项和Sn满足Sn=2an-2n+1,其中n∈N*。

(2)设dn=4n+(-1)n-1λ·2bn(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有dn+1＞dn成立。

54.设A(x1,y1),B(x2,y2)是函数f(x)的图像上任意两点,已知且点M的横坐标为

(1)求证:点M的纵坐标为定值;

(2)若Sn=f+…+求Sn

(3)已知an=n≥2,Tn为数列{an}的前n项和,若Tn＜λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围。

55.已知数列{an}是等差数列,公差d≠0,an≠0(n∈N*),akx2+2ak+1x+ak+2=

(1)求证:当k取不同正整数时,方程都有公共根;

(2)若方程不同的根依次为x1,x2,x3,…,xn,求证：是等差数列。

56.已知等差数列{an}的前n项和为Sn,并且a2=2,S5=15,数列{bn}的前n项和Tn

(1)求数列{an}的前n项和Sn;

57.已知等差数列{an}的前n项和为Sn,并且a2+a4=6,S4=10。

(1)求数列{an}的通项公式;

(2)令bn=an·2n(n∈N*),求数列{bn}的前n项和Tn。

58.已知等差数列{an}的首项a1=1,公差d＞0,且a2,a5,a14分别是等比数列{bn}的第2,3,4项。

(1)求数列{an}和数列{bn}的通项公式;

(2)设数列{cn}对于任意正整数n均有成立,求c1+c2+…+c2015+c2016的值。

59.已知数列{an}是等比数列,其前n项和为Sn。

(1)若S4,S10,S7成等差数列,证明a1,a7,a4也成等差数列;

(责任编辑 徐利杰)