数列及等差数列误区警示

2017-12-02浙江省绍兴一中傅伊岚

中学生数理化(高中版.高二数学) 2017年9期

关键词：公倍数易错式子

■浙江省绍兴一中傅伊岚

数列及等差数列误区警示

■浙江省绍兴一中傅伊岚

数列是一类特殊的函数,一般说来,数列概念、公式都有限制条件或使用前提,特别是等差数列,在解题过程中若忽视了这些限制条件或使用前提,则易导致错误。

易错点一:对数列的概念理解错误

已知有穷数列:5,7,9,11,…,2n+7,其中后一项比前一项大2。

(1)写出此数列的通项公式;

(2)9+4n是否为此数列中的一项?

错解:(1)观察可知此数列为等差数列,a1=5,d=2。

所以此数列的通项公式为an=a1+(n-1)d=5+(n-1)·2=2n+3。

(2)因为9+4n=2(2n+3)+3,所以9+4n是此数列中的第2n+3项。

错解剖析:错解忽视了“有穷数列”这一条件,从而误认为9+4n是数列中的项。

正解:(1)此数列共有n+2项,通项公式为ak=2k+3(k=1,2,3,…,n+2)。

(2)此数列为递增的有穷数列,且末项为2n+7,而9+4n＞2n+7,故9+4n不是此数列中的项。

易错点二:数列的表示方法错误

已知数列{an}满足条件则数列的通项公式为( )。

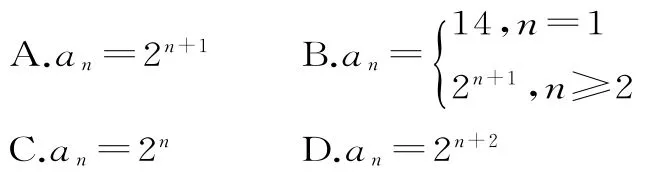
错解:因为2n+5,所以-1)+5。

错解剖析:在上述解答的第二个式子中,应加上限制条件n≥2,因为当n=1时,此式是不成立的。按照第一个式子,1+5,a1=14,在第二个式子中,令n=1,则有矛盾。限制了n≥2之后所解出的通项公式an=2n+1只适合n≥2的情况,对n=1应单列求解。

正解:(1)当n=1时,由已知可求得a1=14。

(2)当n≥2时,由已知得:

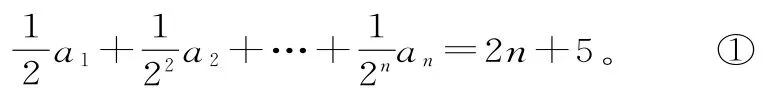
综合(1)、(2)得通项公式an=故应选B。

易错点三:对等差数列概念的理解错误

设两个等差数列分别为2,6,10,…,190和2,8,14,…,200,在它们中间有多少个相同的项?

错解:数列2,6,10,…,190是首项为2,公差d1=4的等差数列;数列2,8,14,…,200是首项为2,公差d2=6的等差数列。相同项构成首项a1=2,公差d=d1·d2=24的等差数列,其通项公式为an=24n-22,其中n为满足an≤190的最大整数,24n-22≤190,解得所以n=8,即两个等差数列中共有8个相同的项。

错解剖析:上述问题中求两个数列相同项的关键是求由相同项构成的新数列的首项和公差。首项a1是对的,将公差认为d=d1·d2是错误的。新数列的公差应该是第一个数列的公差,又是第二个数列的公差,满足这两个条件的公差应该是已知数列的公差的最小公倍数d=12,事实上,通过观察两个数列的相同项:2,14,26,…,也能发现公差d=12。

正解:数列2,6,10,…,190是首项为2,公差d1=4的等差数列;数列2,8,14,…,200是首项为2,公差d2=6的等差数列。相同项构成首项a1=2,公差为4和6的最小公倍数即d=12的等差数列,其通项公式为an=12n-10,其中n为满足an≤190的最大整数,12n-10≤190,解得n≤16所以n=16,即两个等差数列中共有16个相同的项。