内高班预科与高中数学衔接教学的研究——对“一元二次函数”教学中的几点思考

苏华飞

（江门市培英高级中学,广东 江门 529000）

内高班预科与高中数学衔接教学的研究
——对“一元二次函数”教学中的几点思考

苏华飞

（江门市培英高级中学,广东 江门 529000）

内高班预科数学教学一直没有统一。为更好地开展预科与高中数学衔接教学，总结2年预科班教学经验，以一元二次函数教学为切入点，分析教学内容在衔接课程中的作用，提出预科班数学教学内容设计的原则。

内高班；预科；数学教学

一、问题的缘起

内地新疆高中班（内高班）办班已有17年历史，但内高班预科的课程教学普遍处于混乱状态，一方面没有统一教材，课程内容主要是承办学校“摸索式”讲授；另一方面，内高班生源的素质良莠不齐，两极分化严重，给预科班教学带来很大的挑战。总结2年预科班教学经验，以一元二次函数为载体，例谈如何更好地开展内高班预科与高中数学衔接教学，以期为相关教学提供借鉴。

二、本部分内容在衔接课程中的地位与作用

作为初中数学三大函数模型之一，一元二次函数有着广泛的生活应用，是初中函数模块的核心内容，更是高中数学课程的重要载体。人教版必修一以一元二次函数为主要载体，从数形结合的角度阐述函数的基本性质，同时二次函数的载体应用价值在“方程的根与函数的零点”内容中得到进一步的突出，一元二次函数也是一元二次方程与一元二次不等式之间的桥梁，与代数、几何等紧密相关。事实上，一元二次函数的载体应用价值贯穿整个高中数学课程，所以，本部分内容作为预科班初中与高中衔接课程内容，不仅要求学生熟练掌握一元二次函数的相关知识点，更重要的潜在课程目标是培养新疆学生的数形结合思想，为高中数学课程学习奠定基础。

三、本部分教学内容设计的原则

（一）基础性

内高班的学生多数来自新疆各地区偏远农村，数学水平差距较大，部分学生不具备汉语审题能力。在教学内容的设计上首先要立足基础，抓住基本概念，突出基本方法，渗透基本思想。

例1求满足下列条件的一元二次函数的解析式：

（1）已知顶点坐标为(2,-1)，且过点(4,3)；

（2）已知抛物线与x轴交于(1,0)，(3,0)两点，与y轴交于点(0,9)；

（3）已知抛物线过A(2,0),B(0,-1)和C(4,5)3点；

（4）已知二次函数f(x)=ax2+bx+c满足f(x+2)=f(-x+2),又f(0)=3,f(2)=1。

解析：（1）y=(x-2)2-1;（2）y=3(x-1)(x-3);

点评：（1）一元二次函数的解析式是初中数学的重要考点，而灵活运用二次函数的3种表示法是解题的关键；（2）待定系数法是求函数解析式的常用方法。

例2求函数y=-2x2-12x-10图象的开口方向、对称轴、顶点坐标、最小值、与坐标轴的交点坐标，指出当x取何值时，y随x的增大而增大（增函数），当x取何值时，y随x的增大而减小（减函数）？并画出该函数的图象。

解：y=-2(x2+6x)-10=-2(x+3)2+8抛物线的开口向下；对称轴是直线x=-3;顶点坐标为A(-3,8);

当x=-3时，函数有最大值y=8;

当x＜-3时，y随着x的增大而增大；当x＞-3时，y随着x的增大而减小；

令-2(x+3)2+8=0,解得x=-5或x=-1;

令x=0,得y=-10;与x轴的交点坐标是B(-5,0)和C(-1,0),与y轴的交点坐标是D(0,-10)。

采用描点法作图，取关键点A、B、C、D4点，以及点D(0,-10)关于对称轴x=-3的对称点E(-6,-10),通过这5点就可以画出二次函数的简图（图像略）。

点评：（1）配方后易得二次函数的性质，配方法也是解一元二次方程的方法之一；（2）描点法画函数图象的核心在于选取关键点（顶点，与坐标轴的交点，端点等）。

（二）新颖性

在题型的选择上注重与其它知识的结合，拓展学生的数学视野，这是新课程中考和高考命题的新特征：（1）题型新：在传统题型上融入新元素，充分发挥其载体功能；（2）视角新：在知识的交汇处寻找考点，重视考查思维灵活性和接受新信息能力。

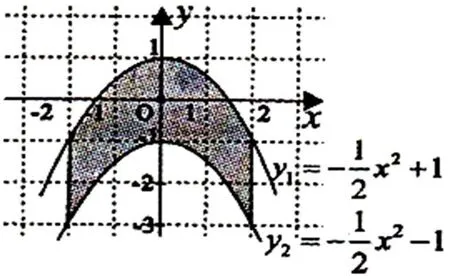
图1 例3示意图

A.8 B.6 C.10 D.4

解析：两条抛物线的顶点坐标分别为（0，1），（0，－1），观察图像易得，阴影部分的面积等于由4条直线x=-2、x=2、y=-1和y=1围成的矩形的面积，S阴影=4×2=8故选A。

例4定义新运算：a×b=a×(1-b),若(a,0),(b,0)是抛物线与x轴的交点坐标，则b×b-a×a的值为( )。

A.0 B.1 C.2 D.与m有关

解析：由题意得a,b是方程的2个根，所以b×b-a×a=b(1-b)-a(1-a)=(b-a)-(b2-a2)=(b-a)[1-(b+a)] =0。

点评：（1）以二次函数为载体考查阴影部分面积的计算，培养学生的观察力；（2）信息题成为新中考、高考的亮点，考查学生接受新知识的能力，给人耳目一新的感觉。

（三）衔接性

预科班的复习既要巩固旧知识，更重要的是为高中的数学教学打基础。所以，在教学内容上要考虑衔接性，融入高中数学的相关知识，渗透相应的数学思想与方法技能。

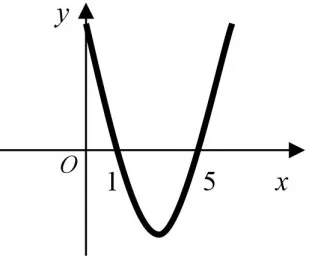
图2 例5示意图

例5观察函数y=x2+mx+n的图象（示意图见图2），探究下列问题：

（1）m=_______，n=_______；

（2）函数的最小值是_______，最大值_______；

（3）当4≤x≤6时，函数的最小值是_______，最大值是_______；

当0≤x≤2时，函数的最小值是_______，最大值是_______；

当0≤x≤5时，函数的最小值是_______，最大值是_______。

（4）当t≤x≤t+1时，讨论函数的最小值情况：

①当对称轴在所给范围左侧时，t_______，y最小= ____________；

②当对称轴在所给范围之间时，t_______，y最小= ____________；

③当对称轴在所给范围右侧时，t_______，y最小= ____________。

总结归纳求二次函数y=ax2+bx+c(a≠0)在某一范围内的极值的步骤：

第一步。先通过配方，求出函数图象的对称轴；

第二步。画简图，根据自变量范围，找相应部分的图像（含字母的一般分3种情况讨论）。

（5）当x=____________时，y=0,即方程x2+mx+n=0的根是____________；

当x＞___或x＜___时，y＞0,即不等式x2+mx+n＞0的由韦达定理（根与系数的关系）得解集是__________；

当___＜x＜___时，y＜0,即不等式x2+mx+n＜0的解集是____________。

注：由抛物线与轴的交点坐标可以确定对应的二次方程的解和一元二次不等式的解集。

（6）展示二次函数y=ax2+bx+c与x轴交点个数的3种图像，探究二次不等式ax2+bx+c＞0或ax2+bx+c＜0(a≠0)的解集。

总结归纳：求二次不等式ax2+bx+c＞0或ax2+bx+c＜0的解集的步骤：

第一步。计算判别式△=b2-4ac,若△≥0,求出相应方程的根；

第二步。画二次函数简图，借助图像得出二次不等式的解集。

例6已知方程x2+(2m-1)x+4-2m=0,求满足下列条件的m的取值范围。

（1）2个正根；

（2）1个根大于2，1个根小于2；

（3）1个根在（-2，0）内，另1个根在（0，3）内。

解析：

解法一：利用韦达定理（略）。

解法二：借助二次函数图象，设f(x)=x2+(2m-1)x+4-2m

点评：（1）数形结合是处理函数问题的重要思想方法，是求二次函数的最值问题、二次不等式的解集问题的共性通法；（2）把方程的根的分布转化为函数问题，这正是必修一“函数与方程”要突出的数学思想方法。

（四）综合性

二次函数集观察分析、作图计算、推理论证于一体，蕴含着形数结合、分类讨论、转换化归等丰富的数学思想，它与代数、平面几何、解析几何等知识有着千丝万缕的联系，教学中要考虑把相关知识点有机地串联起来，全面考查学生的应用能力。

图3 例7示意图

（1）直接写出A、B、C的坐标；

（2）在抛物线对称轴上确定一点Q,使△QBC的周长最小，求出点Q的坐标；

（3）求△PCD面积的最大值。

解析：

（1）A(4,0)、B(-2,0)、C(0,-4);

（2）设抛物线的对称轴交AC于点Q,则Q点即为所求。

因对称轴为x=1,直线AC的解析式为y=x-4,所以所求点Q的坐标是(1,-3)。

（3）设P(x,0)(-2＜x＜4),

因为PD∥AC,所以解得

边PD上的高等于P到AC的距离d=PA×sin45°=

△PCD的面积所以△PCD面积的最大值是3。

点评：（1）面积（距离）的变化问题归根到底是函数的极值问题，关键是确定面积（距离）函数；（2）重视数形结合，充分挖掘图形中隐含的条件。

[1] 苏华飞.一道课后习题的研究性学习[J].中学教学参考，2009（02）：14-15.

[2] 黄之.正确解读教材文本，准确把握教学内容[J].中学数学教学，2016（04）：13-16.

[3] 黄飞跃，李昌贵.在空间品“角”论“距”[J].广东教育：高中版，2008（06）：17-19.

（责任编辑：张宝杰）

苏华飞，男，广东省江门市培英高级中学，数学中学一级教师。