轴向功能梯度变截面Timoshenko梁自由振动的研究

葛仁余， 张金轮， 姜忠宇， 韩有民， 索小永， 牛忠荣

(1.安徽工程大学 力学重点实验室， 安徽 芜湖 241000； 2.合肥工业大学 土木与水利工程学院， 合肥 230009)

轴向功能梯度变截面Timoshenko梁自由振动的研究

葛仁余1， 张金轮1， 姜忠宇1， 韩有民1， 索小永1， 牛忠荣2

(1.安徽工程大学 力学重点实验室， 安徽 芜湖 241000； 2.合肥工业大学 土木与水利工程学院， 合肥 230009)

功能梯度材料可以提高结构的强度、改善质量分布和保证工程结构的完整性，因此轴向功能梯度变截面梁已广泛应用于土木、机械和航空工程。提出了用插值矩阵法计算轴向功能梯度Timoshenko梁自由振动固有频率；基于Timoshenko梁理论，将轴向功能梯度Timoshenko梁自由振动固有频率的计算转化为一组非线性变系数常微分方程特征值问题；运用插值矩阵法可一次性地计算出轴向功能梯度变截面梁各阶振动固有频率，并可同时获取相应的振型函数。该方法对于材料梯度函数和截面几何轮廓的具体形式无任何限制条件，计算结果与现有结果对比，发现吻合良好，表明了该方法的有效性。

变截面梁；横向振动；固有频率；插值矩阵法；功能梯度材料

功能梯度材料(Functionally Graded Material, FGM)是一种新型复合材料，将多种性能各异的材料按照设计意愿，形成材料的物理性能连续变化的组织和结构，同时使不同材料结合部位的界面消失，避免了材料物理性能的不连续性和应力集中，材料的性能在空间沿某个方向连续变化，以满足各种特殊工程结构的需要[1]。

目前，材料性能沿厚度方向梯度变化的功能梯度梁关于弯曲变形、自由振动和稳定性已有了大量的研究，文献[2]假设材料的弹性模量沿厚度方向按指数型函数连续变化，研究了受横向荷载作用的功能梯度简支梁的弹性解。文献[3]开发了一种新型梁单元研究了材料的力学、热学性能沿厚度方向梯度变化的热弹性问题；文献[4]提出遗传算法来优化沿厚度方向梯度变化的功能梯度梁固有频率；文献[5]分析了沿厚度方向按幂律和指数律连续变化功能梯度简支梁的解析解。

相对各向同性均匀性材料，轴向功能梯度梁的振动问题研究比较复杂，因为材料的弹性模量、剪切模量和密度沿轴线方向连续变化，这些性质导致梁结构振动问题数学模型的实质就是求解变系数常微分方程问题，通常情况下很难获得轴向功能梯度梁自由振动的解析解，因此国内有关轴向功能梯度梁振动的研究文献相对较少；文献[6]将非均质锥形变截面Timoshenko梁看作成许多小的均质梁组合进行研究；文献[7]研究了阻尼对非均质变截面Timoshenko梁的影响；文献[8-9]分别运用微分变换单元法和有限元方法研究了轴向功能梯度变截面Timoshenko梁的自由振动和稳定性问题；文献[10]提出了利用Fredholm积分方程来研究轴向功能梯度变截面梁的自由振动问题，并确定了特定边界条件下梁的固有频率；文献[11-12] 利用半逆解法研究了梁的材料性质按特殊形式的多项式函数梯度变化的自由振动问题；文献[13-14] 针对特殊梯度变化情况研究了不同边界条件下功能梯度变截面Eular-Bernoulli梁的自由振动问题。

本文提出采用插值矩阵法(Interporlating Materix Method, IMM)[15]研究轴向功能梯度Timoshenko梁自由振动的一个新途径。基于Timoshenko梁理论推导出功能梯度梁自由振动方程，将轴向功能梯度Timoshenko梁自由振动固有频率的计算转化为一组变系数常微分特征方程的特征值问题求解，运用插值矩阵法求解该变系数常微分方程组，可获得轴向功能梯度梁自由振动前若干阶固有频率及其相应的振型函数，且变系数常微分方程组里出现的所有振型函数及其各阶导函数的计算值具有同等精度，在利用振型函数及其导函数计算梁横向振动的弯矩和剪力时，这是一个显著优点， 而差分法和有限元法求解振型函数导函数的精度是逐次降阶的。

1 基本理论和计算方法

考虑一长度为l且材料性能和截面面积沿轴向x任意连续变化的Timoshenko梁，发生自由振动时，其挠度设为w(x,t)、转角为θ(x,t)。假设材料的弹性模量为E(x)，材料的密度为ρ(x)，截面面积为A(x)，截面转动惯量为I(x)，均为x的函数，即E(x)=E0f1(x)，ρ(x)=ρ0f2(x)，A(x)=A0h1(x)，I(x)=I0h2(x)，G(x)为材料的剪切弹性模量，κ为剪切系数，v为泊松比，其中，E0,ρ0,A0,I0对应于轴向功能梯度梁在左端边界x=0位置材料的弹性模量、密度、截面积和截面惯性矩，如图1所示。

Timoshenko梁的自由振动方程为

(1)

图1 轴向功能梯度变截面Timoshenko梁Fig.1 Schematic of an axially functionally graded Timoshenko beams with varying section

(2)

本文主要考虑梁的自由振动以及谐波振动问题，则

w(x,t)=W(x)sinωt，θ(x,t)=Θ(x)sinωt

(3)

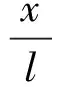
可得

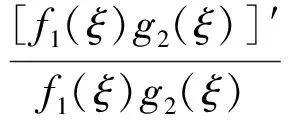
(4)

(5)

式中：r为影响梁横截面转动惯量的无量纲回转半径；s为影响梁剪切变形的无量纲参量；Ω为梁的无量纲固有频率。为描述方便，令

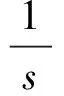
代入式(4)、式(5)可得

Θ″(ξ)+g111(ξ)Θ′(ξ)-g110(ξ)Θ(ξ)+
g121(ξ)U′(ξ)+λq110(ξ)Θ(ξ)=0

(6)

U″(ξ)+g221(ξ)U′(ξ)-Θ′(ξ)-g210(ξ)Θ(ξ)+
λq220(ξ)U(ξ)=0

(7)

为方便描述梁的边界条件，采用标记C，H和F分别表示固定、铰支和自由3种边界条件，如C-F表示梁的边界条件为左端固定、右端自由，本文Timoshenko梁自由振动的边界条件为

简支-简支梁(H-H)

Θ′(ξ0)=0,U(ξ0)=0

Θ′(ξn)=0,U(ξn)=0

固支-固支梁(C-C)

Θ(ξ0)=0,U(ξ0)=0

Θ(ξn)=0,U(ξn)=0

固支-自由梁(C-F)

Θ(ξ0)=0,U(ξ0)=0

Θ′(ξn)=0,U′(ξn)-Θ(ξn)=0

图2为功能梯度梁IMM计算模型，将区间[0,1]划分为n段，0=ξ0,ξ1,ξ2,…,ξn-1,ξn=1，Δli=ξi-ξi-1=1/n利用差分法将变系数常微分方程组中两个函数Θ(ξ),U(ξ)的导数值用区间划分点上的函数值表示。

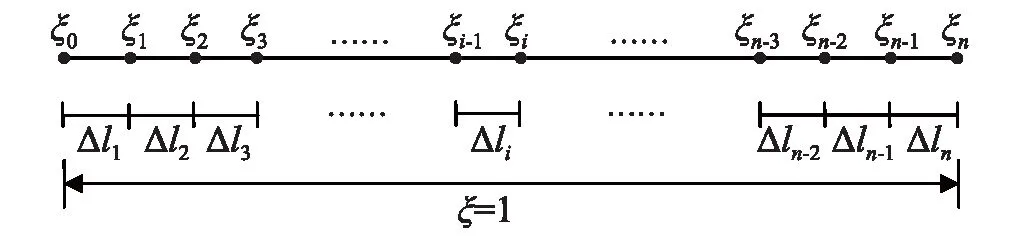
图2 轴向功能梯度梁插值矩阵法计算模型Fig.2 IMM computation mode of an axially functionally graded beams

(8)

式(3)中的Θ″(ξ)和U″(ξ)用插值函数来逼近，设

(9)

式中，Li(ξ)为拉格朗日插值基函数，所以

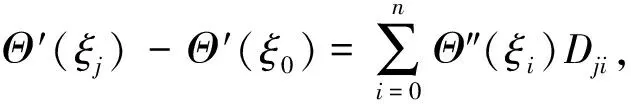
(10)

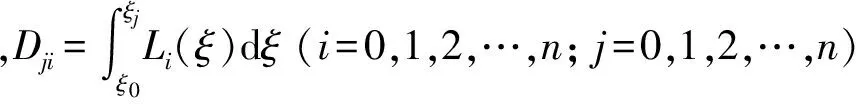
引入向量和矩阵符号

式中，矩阵D称为积分矩阵，仅依赖于插值基函数Li(ξ)，采用二次抛物线插值，其基函数为

将式(6)和式(7)中的Θ(ξ)函数、U(ξ)及其各阶导函数写成向量形式为

Θ′=τΘ(ξ0)+σΘ′(ξ0)+DΘ″=

U′=τU(ξ0)+σU′(ξ0)+DU″=

H1=[τ,σ,D](n+1)×(n+3)

(11a)

将低阶导函数顺次地采用高阶导函数替换，逐步递推可得

Θ=σΘ(ξ0)+DσΘ′(ξ0)+D2Θ″=

U=σU(ξ0)+Dσ·U′(ξ0)+D2U″=

H0=[σ,Dσ,D2](n+1)×(n+3)

(11b)

Θ″=τΘ(ξ0)+τΘ′(ξ0)+IΘ″=

U″=τU(ξ0)+τU′(ξ0)+IU″=

H2=[τ,τ,I](n+1)×(n+3)

(11c)

其中，

Θ={Θ(ξ0),Θ(ξ1),Θ(ξ2),…,Θ(ξn)}T，

Θ′={Θ′(ξ0),Θ′(ξ1),Θ′(ξ2),…,Θ′(ξn)}T，

Θ″={Θ″(ξ0),Θ″(ξ1),Θ″(ξ2),…,Θ″(ξn)}T，

U={U(ξ0),U(ξ1),U(ξ2),…,U(ξn)}T，

U′={U′(ξ0),U′(ξ1),U′(ξ2),…,U′(ξn)}T，

U″={U″(ξ0),U″(ξ1),U″(ξ2),…,U″(ξn)}T

将式(6)和式(7)振动微分方程组中变系数写成对角阵形式

G111=diag(g111(ξ0),g111(ξ1),…,g111(ξn)),

G110=diag(g110(ξ0),g110(ξ1),…,g110(ξn)),

G121=diag(g121(ξ0),g121(ξ1),…,g121(ξn)),

Q110=diag(q110(ξ0),q110(ξ1),…,q110(ξn)),

G221=diag(g221(ξ0),g221(ξ1),…,g221(ξn)),

G210=diag(g210(ξ0),g210(ξ1),…,g210(ξn)),

Q220=diag(q220(ξ0),q220(ξ1),…,q220(ξn)),

(12)

将式(11)和式(12)代入式(6)和式(7)中，则功能梯度Timoshenko梁自由振动方程写成向量形式为

(13a)

(13b)

不失一般性，以两端固支梁(C-C)情况为例进行讨论，则相应的边界条件用向量可表示为

(14)

联立式(13)和式(14)，将Timoshenko梁自由振动控制微分方程和边界条件合并写成矩阵形式为

(15)

2 数值算例与讨论

考虑一长度为l的Timoshenko梁，设无量纲回转半径、剪切系数和材料泊松比分别为r=0.01、κ=5/6、v=0.3，设梁的横截面面积为以下两种情形

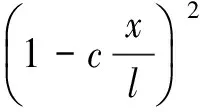
(16)

式中：c为变截面锥度系数；x为从梁的左端起点沿轴线方向的坐标；当c=0时，表示为等截面梁，当c=1时，表示为锥形梁，当clt;0时，表示为梁的横截面从左端到右端逐渐增大。设轴向功能梯度Timoshenko梁的材料由铝和氧化锆组成，它们的弹性模量和密度分别为Ea=70 GPa；ρa=2 702 kg/m3；Ez=200 GPa；ρz=5 700 kg/m3，材料的物理性能随坐标x变化关系为

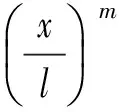
(17)

式中，m为影响材料性能的非均匀性参数。

2.1 变截面锥度系数c对自由振动固有频率的影响

运用IMM计算轴向功能梯度Timoshenko梁自由振动固有频率，在不同的边界条件下，考虑非均匀性参数m=2，锥度系数c取不同的值时，Timoshenko梁自由振动前4阶固有频率计算值如表1～表3所列，表1～表3中给出了网格密度n=10,20,40的IMM计算结果，从表中可知，随着区间划分点数n的加倍，IMM计算结果几乎按数量级加速收敛，当n=40时，计算结果与文献[8]结果完全吻合，说明了IMM计算轴向功能梯度Timoshenko梁自由振动固有频率给出了非常好的结果。由表1～表3计算结果可知，边界条件为C-C、H-H时，随着锥度系数c值的增大，梁的第1阶固有频率减小；而边界条件为C-F时，随着锥度系数值的c增大，梁的第1阶固有频率增大。

2.2材料非均匀性参数m对自由振动固有频率的影响

运用本文的数值计算方法，在不同的边界条件下，考虑锥度系数c=0.2，非均匀性参数m取不同的值时，给出了网格密度n=10,20,40,80时变截面Timoshenko梁自由振动前4阶固有频率计算值如表4～表6所列，当区间划分点数n=40时计算结果开始收敛，与区间划分点数n=80时计算结果趋同，其中第1阶固有频率有5位有效数字相同，第2阶、第3阶固有频率有4位有效数字相同。因此，本文插值矩阵法取区间划分点数n=80时的计算结果可以作为变截面Timoshenko梁自由振动固有频率实际结果。由表4～表6计算结果可见，边界条件为C-C、C-F时，随着非均匀性参数m值的增大，梁的第1阶固有频率减小；而边界条件为H-H时，随着非均匀性参数m值的增大，梁的第1阶固有频率增大。

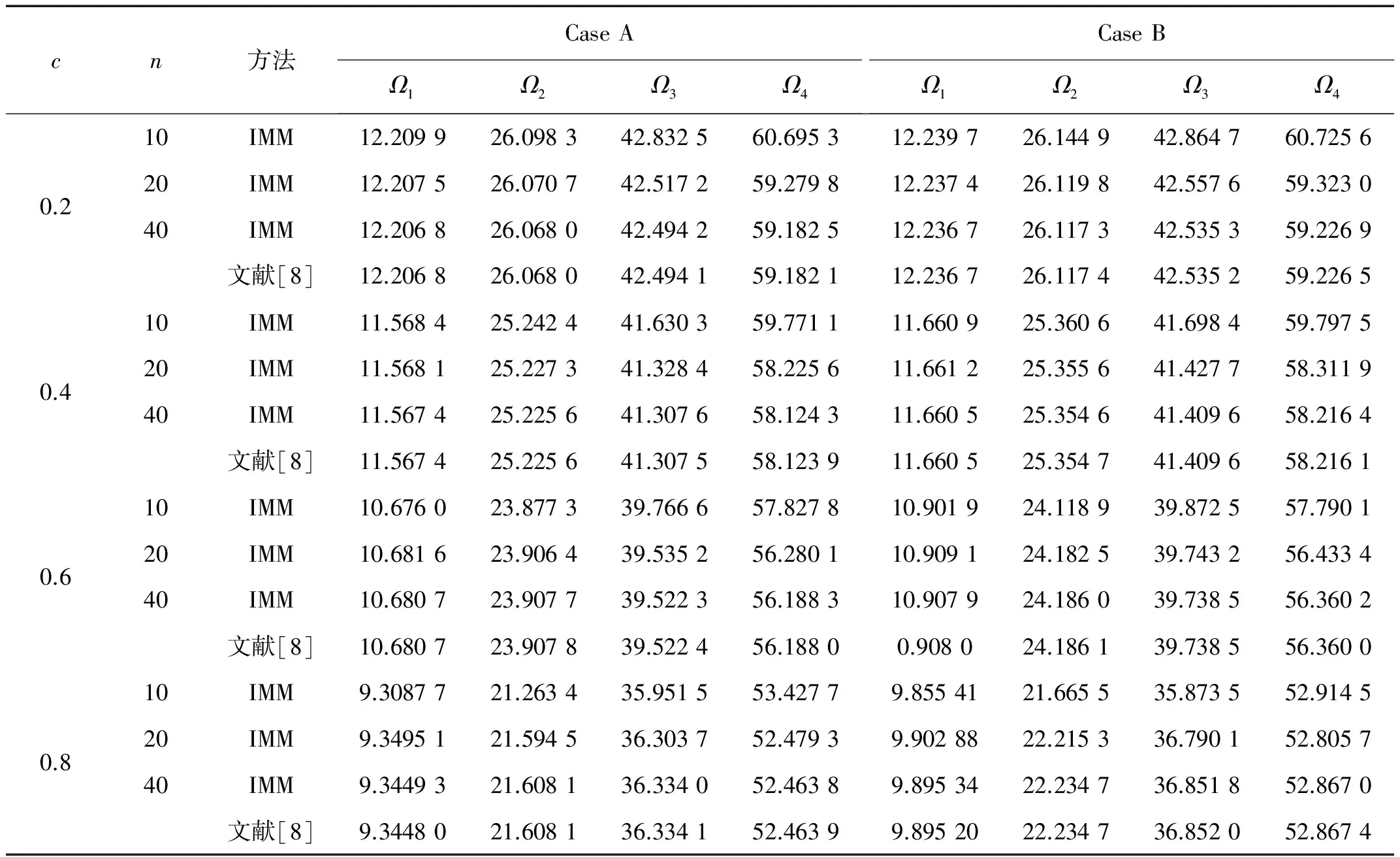
表1 锥度系数取不同值时，两端固支轴向功能梯度变截面Timoshenko梁固有频率计算值

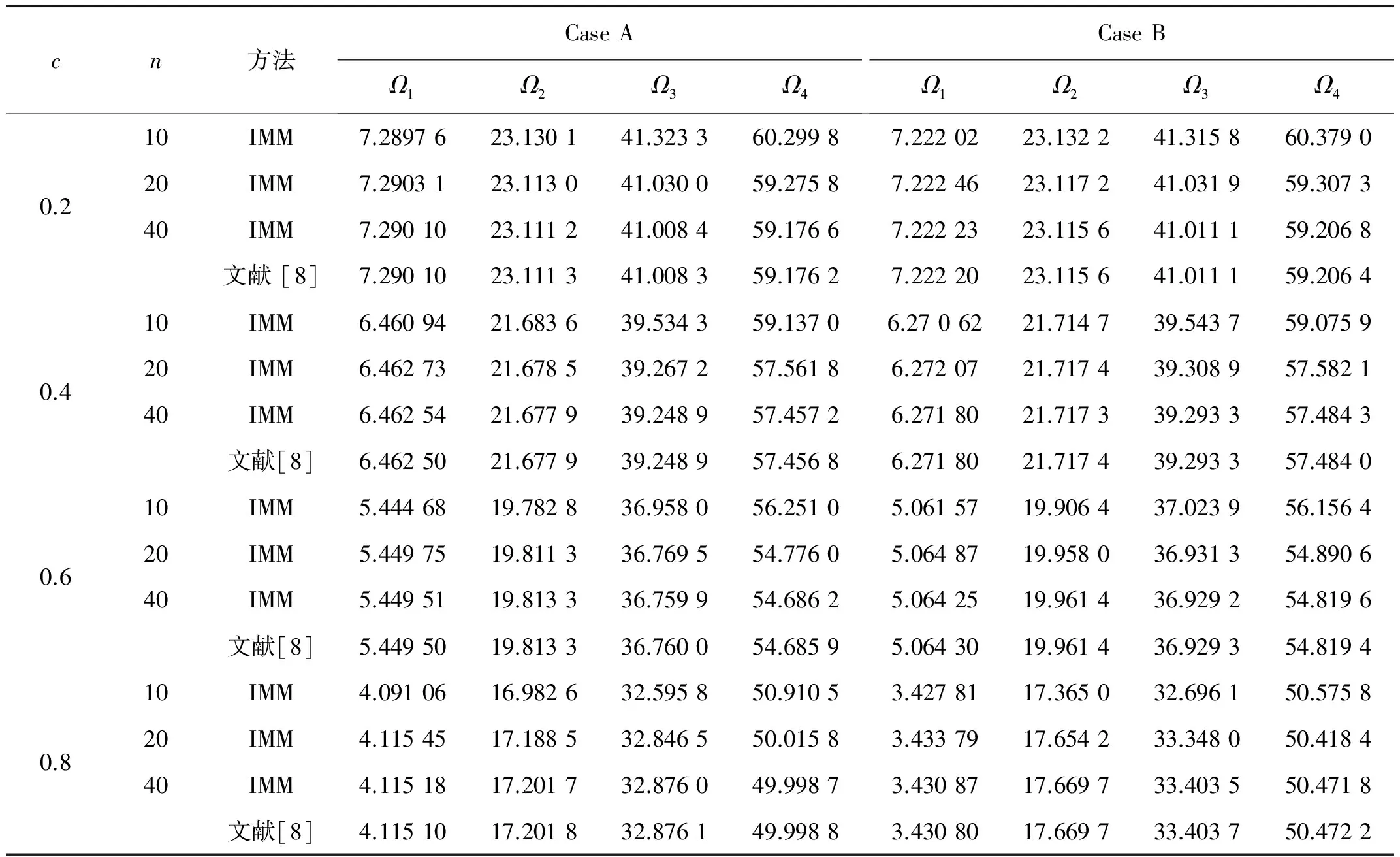
表2 锥度系数取不同值时，两端铰支轴向功能梯度变截面Timoshenko梁固有频率计算值

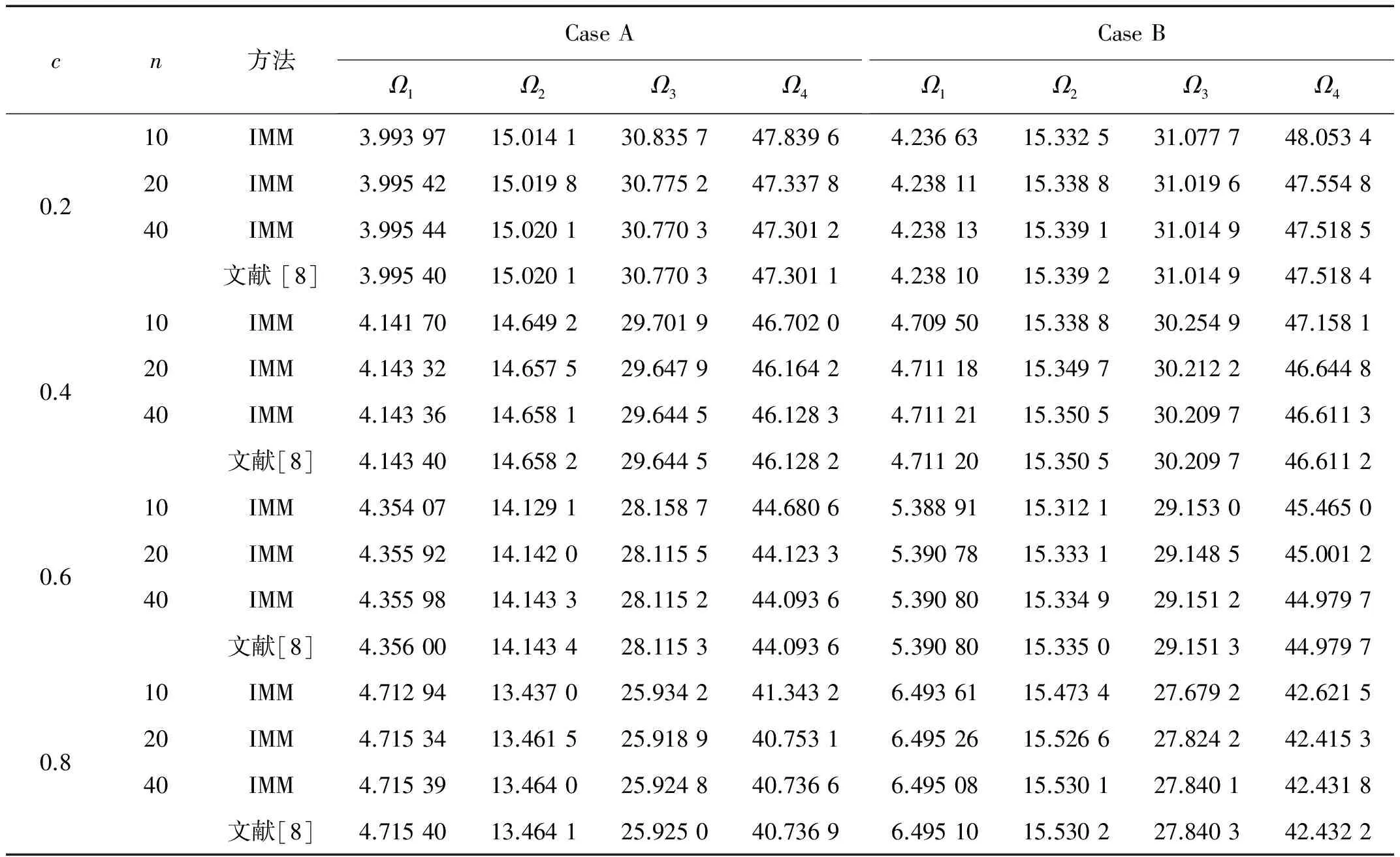
表3 锥度系数取不同值时，一端固支一端自由轴向功能梯度变截面Timoshenko梁固有频率计算值

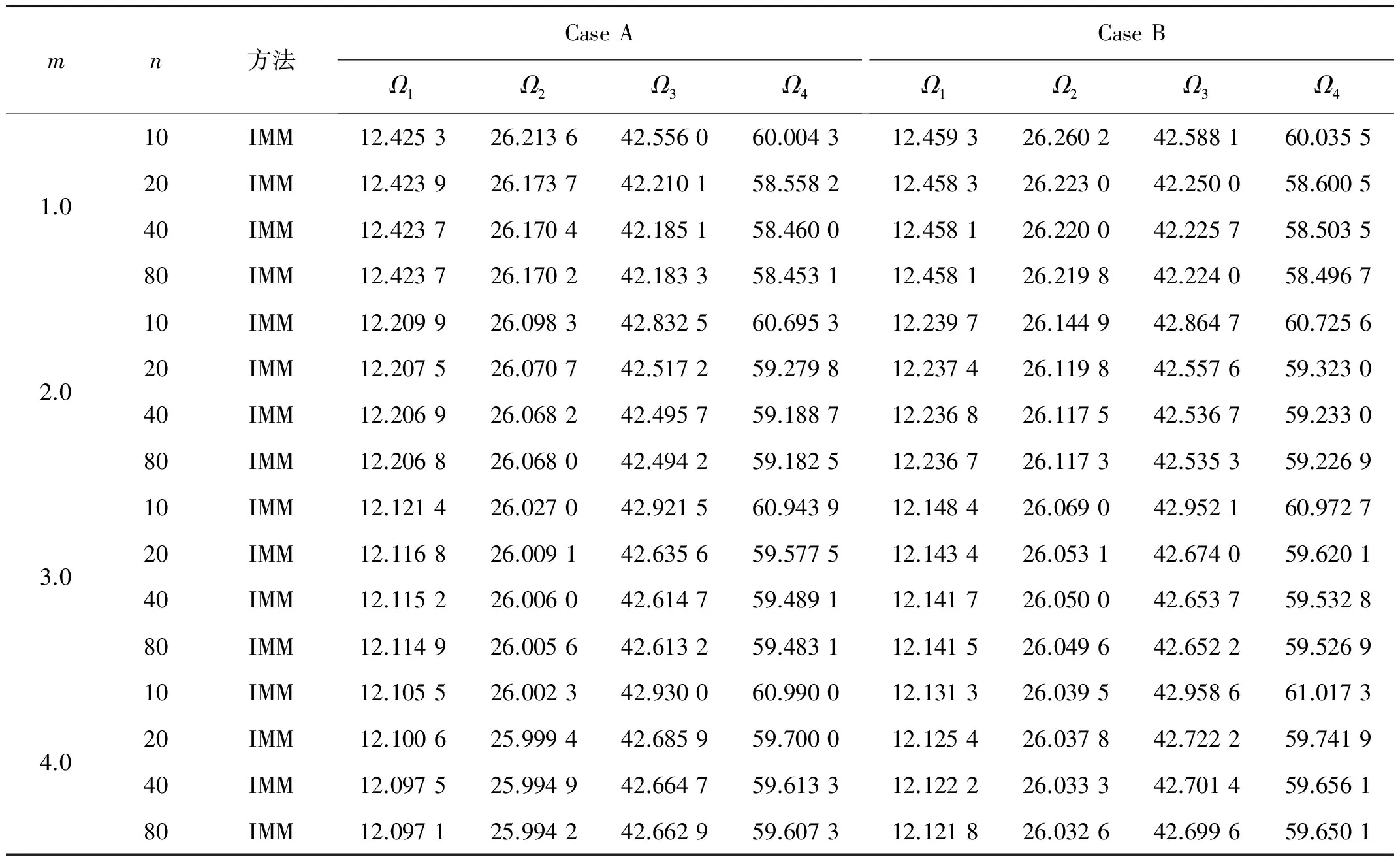
表4 非均匀性参数取不同值时，两端固支轴向功能梯度变截面Timoshenko梁固有频率计算值

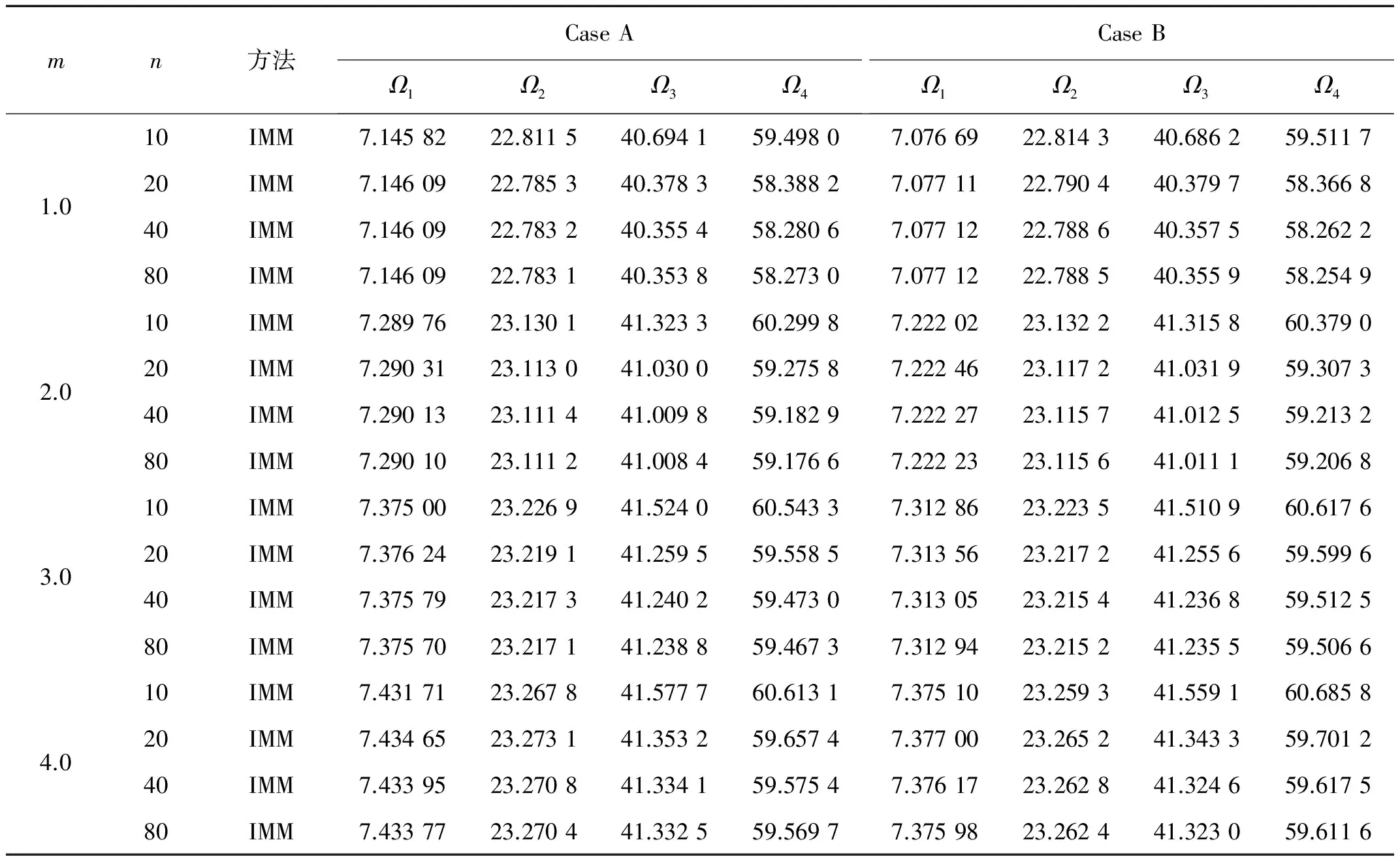
表5 非均匀性参数取不同值时，两端铰支轴向功能梯度变截面Timoshenko梁固有频率计算值

表6 非均匀性参数取不同值时，一端固支一端自由轴向功能梯度变截面Timoshenko梁固有频率计算值

2.3材料非均匀性参数m对等截面梁振型函数曲线的影响

本文的数值计算方法不但可计算出轴向功能梯度Timoshenko梁自由振动前若干阶固有频率，同时相应的振型函数Θ(x)和U(x)一并解出，图3为轴向功能梯度等截面Timoshenko梁在不同的边界条件下材料非均匀性参数m=1和m=5时，第1阶固有频率对应的振型函数Θ(x)和U(x)的分布曲线图，从图3可知，材料的非均匀性参数m对梁自由振动的振型函数的影响不容忽略。

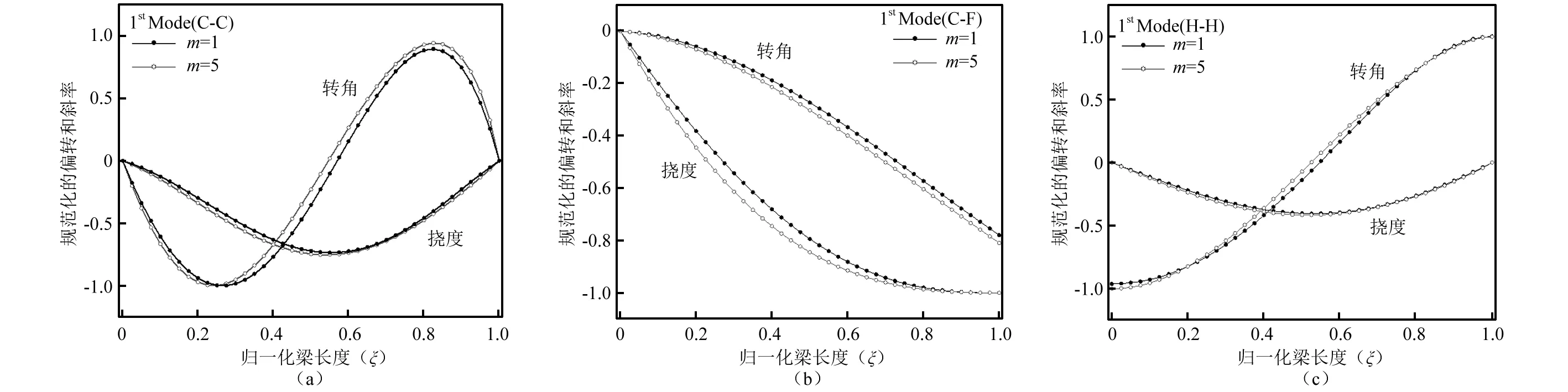
图3 不同的边界条件下材料非均匀性参数m对梁的振型函数分布曲线的影响Fig.3 Variation of the mode shape with the material non-homogeneity parameter (m) for different BCs

4 结 论

本文基于Timoshenko梁理论，将轴向功能梯度变截面Timoshenko梁自由振动固有频率的计算转化为一组变系数常微分方程组特征值问题，然后，运用IMM计算已建立的变系数常微分方程组，从而获得轴向功能梯度变截面Timoshenko梁自由振动前若干阶固有频率，本文具有以下优点：

(1) 轴向功能梯度变截面梁振动问题的复杂性存在于振动方程是一组变系数常微分方程，因此只有一些特殊情况才能获得解析解。本文方法可避免迭代方法计算超越方程，一次性地计算出轴向功能梯度变截面Timoshenko梁的自由振动固有频率。本文方法计算量小、计算精度高和适应性强，具有一定的工程应用价值。

(2) 本文方法既可计算出轴向功能梯度Timoshenko梁自由振动前若干阶固有频率，同时相应的振型函数也一并解出，基于计算结果可知：材料的非均匀性参数对振型函数的分布曲线影响较大。

(3) 解析法分析轴向功能梯度变截面Timoshenko梁的自由振动时，只能局限于特定形式的材料梯度函数和截面几何性质函数，而本文方法对于材料的梯度函数和截面几何轮廓的具体形式无需任何限制条件。

[ 1 ] BIRMAN V, BYRD L W. Modeling and analysis of functionally graded materials and structures[J]. Applied Mechanics Reviews,2007, 60(5): 195-216.

[ 2 ] SANKAR B V. An elasticity solution for functionally graded beams [J].Composites Science amp; Technology, 2001, 61 (5): 689-696.

[ 3 ] CHAKRABORTY A, GOPALAKRISHNAN S, REDDY J N. A new beam finite element for the analysis of functionally graded materials [J]. International Journal of Mechanical Sciences，2003,45(3): 519-539.

[ 4 ] GOUPEE A J, SENTHIL S V. Optimization of natural frequencies of bidirectional functionally graded beams [J]. Structural amp; Multidisciplinary Optimization，2006,32(6): 473-484.

[ 5 ] AYDOGDU M, TASKIN V, Free vibration analysis of functionally graded beams with simply supported edges [J]. Materials amp; Design，2007, 28 (5): 1651-1656.

[ 6 ] TONG X, TABARROK B, YEH K Y. Vibration analysis of Timoshenko beams with non-homogeneity and varying cross-section [J]. Journal of Sound amp; Vibration，1995,186(5): 821-835.

[ 7 ] SORRENTINO S, FASANA A, MARCHESIELLO S. Analysis of non-homogeneous Timoshenko beams with generalized damping distributions [J]. Journal of Sound amp; Vibration，2007, 304(3): 779-792.

[ 8 ] RAJASEKARAN S, TOCHAEI E N. Free vibration analysis of axially functionally graded tapered Timoshenko beams using differential transformation element method and differential quadrature element method of lowest-order[J]. Meccanica, 2014, 49(4): 995-1009.

[ 9 ] SHAHBA A, ATTARNEJAD R, MARVI M T, et al. Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions [J]. Composites Part B Engineering，2011,42(4): 801-808.

[10] HUANG Y, LI X F. A new approach for free vibration analysis of axially functionally gradedbeams with non-uniform cross-section [J].Journal of Sound and Vibration, 2010, 329(11): 2291-2303.

[11] ELISHAKOFF I, CANDAN S. Apparently first closed-form solutions for vibrating in homogeneous beams[J].International Journal of Solids and Structures,2001,38(19): 3411-3441.

[12] CALIO I, ELISHAKOFF I. Closed-form trigonometric solutions for inhomogeneous beam columns on elastic foundation [J]. International Journal of structural Stability and Dynamics, 2004, 4(1): 139-146.

[13] HEIN H, FEKLISTOVA L. Free vibrations of non-uniform and axially functionally graded beams using Haar wavelets [J].Engineering Structures, 2011, 33(12): 3696-3701.

[14] MABIE H H, ROGERS C B. Transverse vibrations of tapered cantilever beams with end loads [J]. Journal of the Acoustical Society of America, 1964, 36(3): 463-469.

[15] NIU Zhongrong, GE Dali, CHENG Changzheng, et al. Determining stress singularity exponents of plane V-notches in bonded bimaterial [J].Journal of University of Science and Technology of China, 2008, 38(3): 314- 319.

FreevibrationanalysisofaxiallyfunctionallyTimoshenkobeamswithanon-uniformcross-section

GERenyu1,ZHANGJinlun1,JIANGZhongyu1,HANYoumin1,SUOXiaoyong1,NIUZhongrong2

(1.KeyLaboratoryforMechanics,AnhuiPolytechnicUniversity,Wuhu241000,China; 2.SchoolofCivilEngineering,HefeiUniversityofTechnology,Hefei230009,China)

Non-uniform beams with varying axially material properties are widely used in civil, mechanical and aeronautical engineering, due to the fact that they can improve distribution of strength and weight, and guarantee structural integrity. In this paper, an interpolating matrix method (IMM) for determining the natural frequencies of free transverse vibration of axially functionally graded Timoshenko beams was proposed. Firstly, based on the Timoshenko beam theory, the governing equations of free vibration analysis of an axially functionally graded Timoshenko beam were transformed into a set of nonlinear characteristic ordinary differential equations with variable coefficients. Then, the interpolating matrix method (IMM) was adopted to solve the established equations. All the natural frequencies of free transverse vibration companying with the corresponding vibration mode functions of the axially functionally graded beam were calculated at a time. Furthermore, the present methods do not pose any restrictions on both the type of material gradation and the variation of the cross section profile. By comparing with the existing results of numerical examples, the validity of the present method was confirmed.

variable cross-section beam; transverse vibration; natural frequency; the interpolating matrix method； functionally graded material (FGM)

国家自然科学基金资助项目(11272111)；安徽省高校自然科学研究重点项目(KJ2016A055)

2016-11-08 修改稿收到日期： 2017-01-20

葛仁余 男，博士，副教授，1969年生

张金轮 男，博士生，讲师，1984年生

O326

A

10.13465/j.cnki.jvs.2017.22.025