非线性单摆系统的Hopf分岔

游 泳

(北京理工大学 珠海学院，广东 珠海 519088)

非线性单摆系统的Hopf分岔

游 泳

(北京理工大学 珠海学院，广东 珠海 519088)

以单摆系统为例，将Wiggins提出的Hopf分岔条件进行了具体计算。从理论上获得了单摆系统发生次谐分岔的方式，并用数值模拟方法验证了结果的正确性；将Melnikov方法推广到二频驱动情况，由二频驱动单摆的Hopf分岔条件得出存在奇-奇阶次谐分岔和奇-偶阶次谐分岔。数值模拟结果与理论分析一致，表明Melnikov方法可以处理多频驱动系统的Hopf分岔问题。

单摆系统； Melnikov函数； Hopf分岔

摆系统广泛存在于机械、电子、地震预测等各个领域中，是非常重要的基础，已被许多人研究。文献[1]用实验方法研究了受迫摆的混沌态和通向混沌道路，表明以对称破缺为先兆，经周期倍化、间歇行为和周期3分岔到混沌。文献[2-6]分别对参数激励摆的混沌区、逃逸区、旋转解等方面作了研究，文献[7]对带有参数和激励摆的复杂动力学问题作了讨论。文献[8-9]用Melnikov方法分析了弱阻尼与参数激励单摆的同宿分岔、次谐分岔和混沌问题，文献[10-11]用Melnikov理论分别讨论了硬弹簧Duffing系统和Duffing-Van der pol系统的次谐分岔。但是，对单摆系统的次谐分岔未见报导。

(1)

式中：x为摆离开最下端平衡位置的角度；δ′为阻尼系数；f′和ω分别为外驱动幅度和角频率。 这里δ′、f′、ω和t均已无量纲化。

单摆系统式(1)是处理摆动问题的经典模型，如航空动力学装置、地震预测装置、矿山筛分机械、机器人等高速旋转设备都是建立在单摆模型上的。文献[12]用数值模拟方法发现，受迫保守单摆系统中存在亚Hopf分岔。而Hopf分岔是动态分岔，是对系统结构稳定性的否定，对于结构不稳定的系统，一个小扰动就可能破坏轨线的拓扑等价。此外，文献[13]对倒摆的混沌运动做了实验研究，实验中发现3/1次谐分岔，该倒摆模型与式(1)仅差一个线性项。文献[8]对文献[13]中倒摆方程作了近似，用Melnikov方法对倒摆近似方程的次谐分岔问题做了研究，结果未能解释实验上的3/1次谐分岔。还有，Melnikov方法是否能处理多频驱动的Hopf分岔问题？这些问题促使本文进一步研究单摆系统式(1)的Hopf分岔问题。

1 Melnikov函数方法的Hopf分岔条件

考虑平面系统

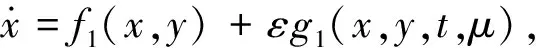
(2)

在ε=0的情况下， 式(2)为哈密顿系统

(3)

对式(3)可以进行作用-角变量变换，即

I=I(x,y),θ=θ(x,y)

(4)

其逆变换为

x=x(I,θ),y(I,θ)

(5)

式中，θ以2π为周期。

用式(3)周期轨道qk=(x,y)所围面积来定义作用量I， 则归一化作用量

(6)

由于这个面积不随时间变化，而角量θ随时间线性变化，则有

(7)

式中，Ω(I)为式(3)周期运动的角频率。

变换式(5)是辛的，雅可比矩阵的行列式等于1。即

(8)

对于扰动式(2)， 满足谐振条件nT1=mT(n、m互质，T1为无扰轨道qk的周期，T为外驱动的周期)时的次谐Melnikov函数为[14-15]

(9)

式中：f∧g=f1g2-f2g1； trDf为雅可比矩阵Df的迹, 对于哈密顿系统有trDf=0。 则式(9)为

(10)

当(x,y)→(I,θ)， 则Mm/n(k,t0,μ)→Mm/n(I0,θ0,μ)≡M1(I0,θ0,μ)； 且I=I0;θ0=Ω(I)t0。

在(I,θ)坐标系中Hopf分岔条件为

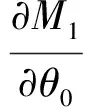
(11)

(12)

其中，

(13)

2 单摆系统的次谐分岔

令δ′=εδ，f′=εf, 则式(1)可表示为

(14)

式中，ε为小量， 式(14)为近哈密顿系统。

2.1 无扰单摆系统的周期解[17]

令式(14)中的ε=0， 得无扰系统

(15)

其哈密顿量为

(16)

式(15)的不动点为(nπ,0) (n=0,±2,±4,…为中心，n=±1,±3,±5,…为鞍点)，周期解为

qk=(x,y)=(2 arcsin(ksn(t,k)),
2kcn(t,k), 0lt;klt;1

(17)

式中： snt、 cnt分别为椭圆正弦函数和椭圆余弦函数。 闭轨qk的周期为T1=4K(k)；K(k)为第一类椭圆积分；k为椭圆函数的模。将式(17)代入式(16)得

(18)

2.2 单摆系统Hopf分岔条件的计算

对于式(14)，由式(10)可得次谐Melnikov函数为

(19)

将式(17)代入式(19)完成积分得

M1(k,t0,μ)=

(20)

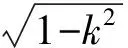
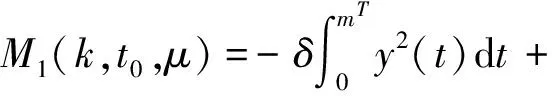
式中，nqk为沿闭轨qk旋转了n圈。上式的第一个积分用式(6)表示，对第二个积分进行分部积分，则得次谐Melnikov函数

M1(I0,θ0,μ)=

(21)

与式(20)比较可得

(22)

于是，在(I,θ)坐标系中的次谐Melnikov函数为

M1(I0,θ0,μ)=

(23)

(24)

由式(13)和式(14)可得

R(I0,θ0,μ)=-δmT

(25)

(26)

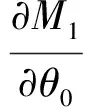
(27)

通过选择θ0总可使条件式(26)和式(27)同时成立。由式(22)和式(24)可得

(28)

由以上校核单摆系统的Hopf分岔条件可知：

(1) 由于单摆系统式(14)满足式(11)和式(12)中的Hopf分岔条件，所以， 当ω与Ω之间满足次谐共振条件式(29)时，如果减小阻尼使参数δ变为0，则系统式(14)通过Hopf分岔，从非线性阻尼运动突变为无阻尼的周期m(奇数)运动，分岔前后的轨线拓扑不等价。

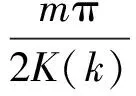
(29)

(2) 单摆系统式(14)只存在m/1=1/1，3/1，5/1，…的奇数阶次谐分岔，不存在m/1=2/1，4/1，6/1，…的偶数阶次谐分岔，与文献[12]数值仿真结果吻合，也解释了倒摆实验中出现的3/1次谐分岔。文献[8]中的系统式(1)与系统式(14)仅在于扰动项不同，其中出现m/1=2/1，4/1，6/1，…的偶数阶次谐分岔，可见，次谐分岔方式与扰动形式有关。

(3) 系统式(14)的Hopf分岔仅与驱动频率ω有关，而与驱动的幅度f无关。

(4) 根据式(29)可得单摆系统的Hopf分岔曲线，如图1所示。

图1 Hopf分岔曲线Fig.1 Hopf bifurcrcation curve

2.3 数值模拟

数值模拟时，由图1确定参数(k,ω)， 在周期轨道qk上取初值来求解式(14)。

2.3.1 固定m,f， 改变k

固定f=0.025，m=3, 取参数(k,ω)=(0.02，2.999 7)，(0.1，2.992 48)，(0.68，2.558 43)，(0.7，2.361 74)，在分岔点作系统式(14)的Poincare截面，呈现3/1阶次谐分岔，如图2所示。m为其他奇数值时， 与m=3的情况类似， 每个闭轨qk上排布着m(奇数)个Hopf圈， 即产生m/1(m为奇数)阶次谐分岔。 当m为偶数时，数值模拟表明闭轨qk上没有Hopf圈产生，表明不发生偶数阶次谐分岔。数值模拟结果与理论分析符合。

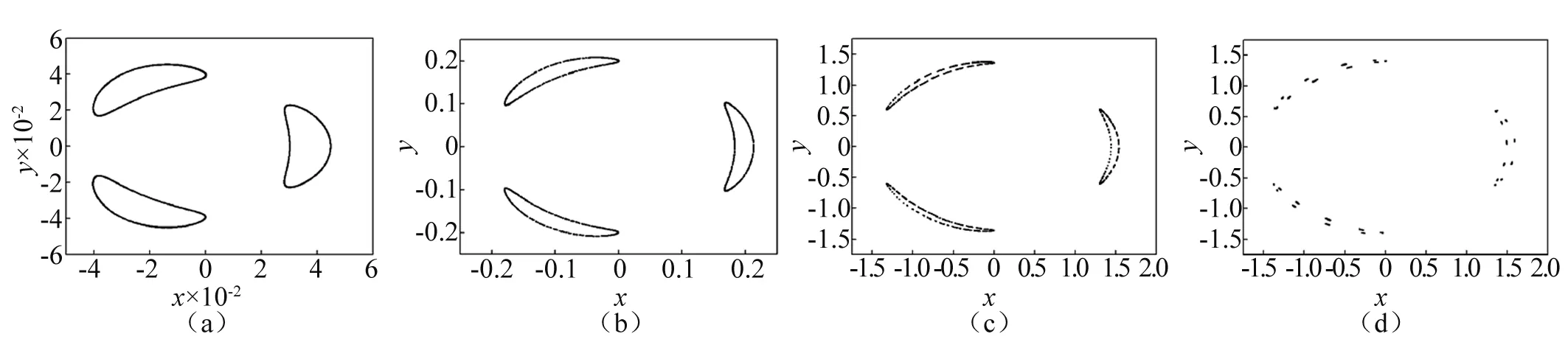
图2 3/1阶次谐分岔产生的Hopf圈Fig.2 Hopf circles of 3/1 subharmonic bifurcation

2.3.2 固定f与k，改变m

固定f=0.25，k=0,2， 取(m,ω)=(1，0.989 87)，(3，2.996 962)，(5，4.949 36)，(9，8.908 85)，用这些参数在分岔点作系统式(14)的Poincare截面，出现m/1=1/1,3/1,5/1,7/1,9/1,…阶次谐分岔，如图3所示。与理论预言完全一致。

图3 不同阶次谐分岔产生的Hopf圈Fig.3 Hopf circles of different orders subharmonic bifurcation

2.3.3 固定m,ω与k，改变f

在m=5的分岔曲线上取ω=4.949 36，k=0.2， 将εf从0.25一直调至0.65， 闭轨qk(k=0.2)都发生5/1阶次谐分岔，与参数f无关，f的大小仅改变Hopf圈裂开的程度，如图4所示。这一结果与理论预言一致。

数值研究表明， 当f大于某个值后，次谐分岔消失。作者认为，这可能是f大到一定程度后，驱动项不能看作微扰，导致次谐Melnikov函数的Hopf分岔理论失效。

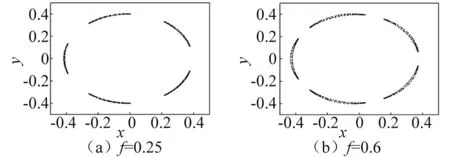
图4 Hopf分岔与驱动强度的关系Fig.4 Relattion of Hopf bifurcation and drive intensty

3 二频驱动的单摆系统的次谐分岔

在实际问题中，系统往往受到多个不同强度、不同频率的周期性外力的驱动。例如，电路系统往往是在多个信号同时激励下工作。因此，研究多频驱动不仅有理论意义，而且有应用价值。

3.1 二频驱动问题的理论分析

对式(14)再加上一个周期驱动，使之成为

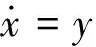
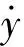
(30)

当系统式(30)满足谐振条件nTk=m1T1=m2T2(n与m1、m2互质,Tk=4K(k)，T1=2π/ω1，T2=2π/ω2)时的次谐Melnikov函数为

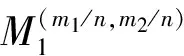
(31)

将式(17)代入式(31)得

(32)

将式(32)用作用-角变量表示，则

(33)

其中，

(34)

由式(13)得

R(I0,θ0,μ)=-δmT

(35)

根据式(33)～式(35)可以证明， 除n≠1,m1、m2均为偶数外，可以通过选择θ0使式(11)和式(12)得以满足。

综上所述，可得二频驱动情况下的有关结论：

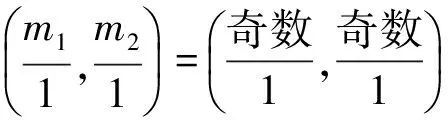
(36)

(2) 根据式(33)中n=1,m1,m2均为奇数的情况可知，Hopf分岔条件与两驱动幅度f1、f2有关。即二频驱动的单摆，其奇-奇阶次谐分岔与两驱动幅度f1、f2有关，这与单频驱动的情况不同。

(3) 由式(36)可得二频驱动单摆系统的Hopf分岔曲线，如图5所示。

(a)

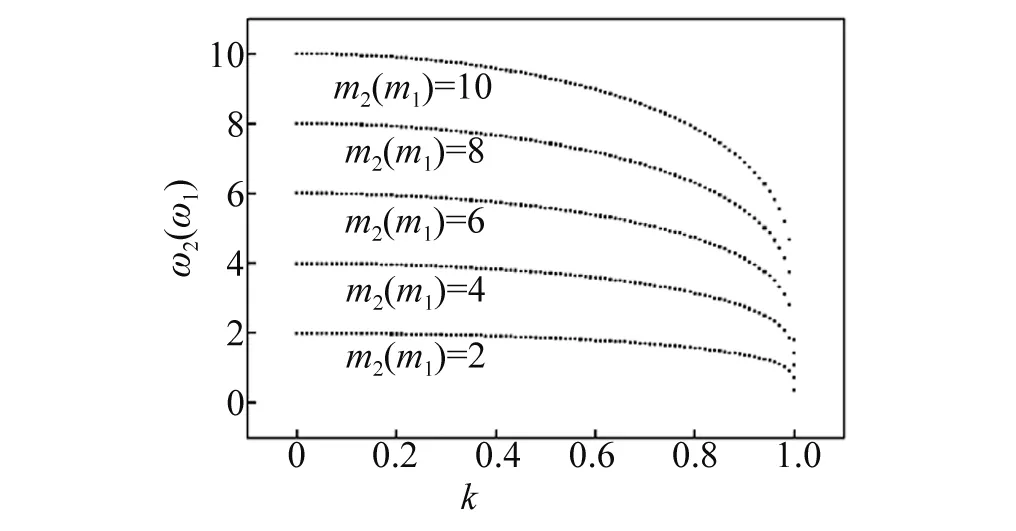
(b)图5 二频驱动问题的次谐分岔曲线Fig.5 Subharmonic bifurcation curve in two-frequency drives

3.2 二频驱动问题的Hopf分岔的数值模拟

(37)

这种情况数值模拟时，参数m1、m2、ω1、ω2、k由式(36)确定。

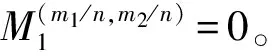
(38)

式中：χ=f2/f1;γ=m2/m1;c=m1π/2。

3.2.1 奇-偶阶Hopf分岔的数值模拟

在图5上取参数(k,ω1)和(k,ω2)， 即用频率分别为ω1,ω2的两个外力驱动周期轨qk。 例如取(k,m1,ω1,m2,ω2,f1,f2,δ)=(0.2,3,2.969 62,4,3.959 49,0.25,0.25,0)，用初值(t,x0,y0)=(0,0,0.4)求解方程式(30)， 获得Poincare截面如图6(a)和图6(b)所示。 发生(m1/1,m2/1)=(3/1,4/1)阶次谐岔。同理，取(k,m1,ω1,m2,ω2,f1,f2,δ)=(0.4,3,2.873 41,12,11.493 63,0.25,0.25,0)，用与k=0.4相应的初值求解方程式(30)， 获得Poincare截面如图6(c)和图6(d)所示，出现(m1/1,m2/1)=(3/1,12/1)阶次谐分岔。 若取m1=10,m2=8， 则得Poincare截面如图6(e)和图6(f)所示。将图6(e)、图6(f)两图中的小线段放大后， 发现是折线而不是Hopf圈(如图6(e)中的放大图所示)。因此，不会发生偶-偶阶次谐分岔，与理论预言一致。

图6 二频驱动问题：有奇-偶阶Hopf分岔，无偶-偶阶Hopf分岔Fig.6 Odd-even Hopf bifurcation in two-frequency drives

3.2.2 奇-奇阶Hopf分岔的数值模拟

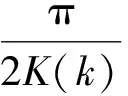
例如，取(χ,γ,m1Ω,m2Ω,k)=(0.1,0.6,5×0.788 01,3×0.788 01,0.799)， 求解系统式(30)得Poincare截面如图7 (a)所示。取(χ,γ,m1Ω,m2Ω,k)=(0.1,0.6,15×0.788 01,9×0.788 01,0.799)求解式(30)得Poincare截面如图7(b)所示(放大图中每一线段都是Hopf圈)。均是奇-奇阶次谐分岔，与理论预言一致。

图7 二频驱动问题：奇-奇阶Hopf分岔Fig.7 Odd-odd Hopf bifurcation in two-frequency drives

4 结 论

综上所述，对单摆系统闭轨的次谐分岔有如下结论：

(1) 次谐Melnikov函数方法对处理多频驱动的Hopf分岔问题也适用，但随驱动数增加，分析难度也迅速加大。

(2) 次谐分岔仅发生在保守情况下，耗散因素将消除次Hopf分岔，次Hopf分岔产生的机制是次谐共振。

(3) 单频驱动情况，仅产生奇数阶次谐分岔，且Hopf分岔的条件仅与驱动频率有关，与驱动强度无关。

(4) 在双频驱动下，可以产生奇-偶和奇-奇阶次谐分岔，但不会出现偶-偶阶次谐分岔.其中奇-奇阶Hopf分岔条件不仅与驱动频率有关，还与驱动幅度有关。

[ 1 ] HUMIERES D, BEASLY M R, HUBERMAN B A, et al. Chaotic states and routes to chaos in the force pendulum[J]. Physical Review A, 1982,26(6): 3483-3492.

[ 2 ] BISHOP S R, CLIFFORD M J. Zones of chaotic behavior in the parametrically excited pendulum[J]. Journal of Sound amp; Vibration, 1996,189(1): 142-147.

[ 3 ] CLIFFORD M J, BISHOP S R. Approximating the escape zone for the parametrically excited pendulum[J]. Journal of Sound amp; Vibration, 1994,172(4): 572-576.

[ 4 ] CLIFFORD M J, BISHOP S R. Rotating periodic orbits of the parametrically excited pendulum[J]. Physics Letters A, 1995,201(2/3): 191-196.

[ 5 ] GARIRA W, BISHOP S R. Rotating solutions of the parametrically excited pendulum[J]. Journal of Sound amp; Vibration, 2003,263(1): 233-239.

[ 6 ] SUDOR D J, BISHOP S R. Inverted dynamics of a tilted parametric pendulum[J]. European Journal of Mechanics-A/Solids , 1996,18(3): 517-526.

[ 7 ] JING Zhujun, YANG Jianping.Complex dynamics in pendulum equation with parametric and excitations I[J].International Journal of Bifurcation and Chaos, 2006,16(10): 2887-2902.

[ 8 ] 谢柏松.单摆运动的同宿轨道分岔、次谐分岔和混沌[J].北京师范大学学报(自然科学版)， 2000，36(5): 631-633.

XIE Baisong.Bifurcation of homoclinec orbit and subharmonic bifurcation and chaos for single pendulum motion[J].Journal of Beijing Normal University(Natural Science), 2000,36(5): 631-633.

[ 9 ] 牛治东、吴光强. 随机激励下汽车非线性悬架系统的混沌研究[J].振动与冲击， 2016,35(17): 39-43.

NIU Zhidong, WU Guangqiang. Chaos of a vehicle nonlinear suspension system under stochastic excitation[J].Journal of Vibration and Shock, 2016,35(17): 39-43.

[10] 郑吉兵，谢建华，孟光.近哈密顿系统的Hopf分岔[J].力学学报， 2001,33(1): 134-141.

ZHENG Jibing, XIE Jianhua, MENG Guang.Hopf bifurcation of a perturbed Hamiltonian system[J]. Acta Mechanica Sinica, 2001,33(1): 134-141.

[11] 符五久.Duffing-Van der pol系统的Hopf分岔[J].振动与冲击， 2010,29(7): 204-209.

FU Wujiu. Hopf bifurcation of a Duffing-Van der pol system[J].Journal of Vibration and Shock, 2010,29(7): 204-209.

[12] 符五久，饶黄云.单摆系统通向混沌的道路[J].大学物理， 2008,27(1): 5-10.

FU Wujiu, RAO Huangyun.The roads to lead chaos in the single pendulum[J].College Physics, 2008,27(1): 5-10.

[13] DUCHCENE B, FIACHER C W, GRAY C G,et al.Chaos in the motion of an inverted pendulum:an undergraduate laboratory experiment[J]. American Journal of Physics，1991,59(11): 987-992.

[14] YAMGOUÉ S B, KOFANÉ T C. The subharmonic melnikov theory for damped and driven oscillators revisited[J]. International Journal of Bifurcation and Chaos, 2002,12(8): 1915-1923.

[15] 周凌云，王瑞丽，吴光敏，等.非线性物理理论及应用[M].北京：科学出版社，2000:166-167.

[16] WIGGINS S.Introduction to applied nonlinear dynamical systems and chaos[M]. New York: Spring-Verlag, 1990.

[17] 佘守宪.非线性振动、非线性波与Jacobi椭圆函数[J]. 大学物理， 2004,23(1): 3-8.

SHE Shouxian. Nonlinear vibration nonlinear wave and Jacobi elliptic function[J]. College Physics, 2004,23(1): 3-8.

Hopfbifurcationinnonlinearforcedsinglependulumsystems

YOU Yong

(ZhuHai Campus, Beijing Institute of Technology, Zhuhai 519088, China)

Based on the necessary and sufficient conditions for existence of Hopf bifurcation, the ways to generate subharmonic bifurcation for a single pendulum system were provided. Furthermore, this paper presented an application of the Melnikov method in a two-frequency-driven single pendulum system. The Hopf bifurcation and its conditions were discussed and its application illustrates that the method can solve many problems of Hopf bifurcation in a multi-frequency-driven single pendulum system.

single pendulum system; Melnikov function; Hopf bifurcation

2016-11-24 修改稿收到日期： 2016-12-30

游泳 男，硕士，副教授，1976年生

O322；O415.6

A

10.13465/j.cnki.jvs.2017.22.017