基于位移的重力坝地震易损性分析方法

马智勇， 张 伟， 周 强， 唐可人

( 1. 广西大学 土木建筑工程学院，南宁 530004; 2. 广西大学 工程防灾与结构安全教育部重点实验室，南宁 530004)

基于位移的重力坝地震易损性分析方法

马智勇1,2， 张 伟1,2， 周 强1,2， 唐可人1,2

( 1. 广西大学 土木建筑工程学院，南宁 530004; 2. 广西大学 工程防灾与结构安全教育部重点实验室，南宁 530004)

针对重力坝地震易损性分析中存在的性能指标参数敏感性大且难以获取、震害等级定量划分困难的问题，提出了基于位移性能指标和相应震害等级划分的重力坝易损性分析方法。选取坝顶和坝颈相对坝踵的顺河向位移作为性能指标，合理选取输入地震波，采用非线性动力时程分析研究了性能指标与破坏形态及结构损伤间的相关性，提出了震害等级的五级划分标准。结合SAC-FEMA的易损性概率分析方法，建立了基于位移的重力坝地震易损性分析方法，可估算重力坝在各级地震作用下出现各级震害的概率，为重力坝抗震设计、地震灾害预测和风险分析提供易损性分析基础。

重力坝；地震易损性分析；基于位移；性能指标；震害等级

我国重力坝设计建设成就卓越，这些大坝对国民经济发展和水资源合理利用起到了重要作用[1]，同时重力坝是关键的挡水建筑物，在极端荷载下失事将会直接威胁下游的生命财产安全。地震是引起重力坝破坏的主要灾害之一[2-3]，开展其抗震安全研究是十分必要的。地震易损性分析可以预测各级地震作用下重力坝发生不同损伤的概率，可为坝体结构抗震安全评价、损失估计和抗震减灾策略提供依据，是目前重力坝抗震安全研究中的热点问题[4-9]。

目前，地震易损性分析主要分为经验分析法和理论分析法。经验分析法，也称为统计分析法，是利用已有的地震记录和震害资料进行易损性分析，要求有足够的震害资料作为统计样本，主要适用于群体建筑物的震害预测[10]，较难应用于地震资料匮乏的坝工结构地震易损性分析中。理论分析法通过理论计算求得结构地震响应，再利用地震响应与震害程度的关系来判别结构震害程度，可直接应用于单体建筑物中[11]，是坝工结构易损性分析主要采用的方法[12-14]。重力坝地震易损性分析中，选择描述震害程度的性能指标，以及划分相应的震害等级是关键问题，目前研究者主要采用以下几种选择和划分方法：Abdelhamid等提出以薄弱部位应力状态为主要性能指标，并给出了相应四级震害等级的划分标准；李晓燕等[15]提出了以损伤破坏形态为性能指标的五级震害等级划分标准；沈怀至等[16-17]提出了基于损伤指数的性能指标，并分别给出了相应的四级和五级震害等级划分标准；沈怀至等综合考虑坝基交界面屈服状态、坝体薄弱部分应力状态和塑性形变等多指标法，并给出了相应的震害等划分标准。

采用传统的应力状态为主要性能指标简单易行，符合传统设计观念，但震害预测偏于局部化、难以反应结构整体震害，同时存在应力结果对计算网格和参数十分敏感的问题[18-19]；采用损伤破坏形态为性能指标能直观地反应震害发展过程，但较难从定量角度将损伤破坏形态与震害等级一一对应；采用基于应力损伤指数的性能指标建立了坝体破坏形态与震害等级间的定量关系，但坝体子区域的划分、权重系数的确定仍较主观且难以实际监测；采用综合指标法能较全面地反映震害特征，但存在应用较为不便，且各单项指标分析中也存在前3种方法遇到的问题。研究表明，在结构分析中，损伤、强度、刚度、延性等都与位移有关，结构位移能较全面表征结构刚度和强度退化状态，与结构主要震害形态存在对应关系，易于定量制定震害等级标准，同时作为大坝安全监测的基本指标，可根据实测数据为震后坝体维护加固提供科学依据，位移作为性能指标已普遍在土木工程地震易损性分析中[20-22]得到认可，并已在坝工[23]、水电站厂房[24]和桥梁[25]地震易损性分析中得到应用。

鉴此，本文选取重力坝坝顶相对坝踵的顺河向位移(以下简称为坝顺顶河向位移)为作为主要性能指标，同时考虑到强震常引起重力坝严重损伤而导致的坝头破坏状况，造成溃坝阶段坝顶顺河向位移衡量可能失效问题，选取坝颈相对坝踵的顺河向位移(以下简称为坝颈顺河向位移)作为溃坝阶段的补充性能指标，并提出了相应的五级震害等级划分标准，结合增量动力分析法(Incremental Dynamic Analysis, IDA)和SAC-FEMA的超越概论分析法，提出了重力坝易损性分析法，为混凝土重力坝的抗震安全评价、损失估计和抗震减灾策略提供参考。

1 重力坝地震易损性分析步骤

地震易损性表达了结构体系在不同强度地震下性能水准的条件概率

F(X)=P[Rgt;LS|IM=X]

(1)

式中：F(X)为易损性概率；R为性能指标；LS为各震害等级的性能水准；IM为地震动参数；X为地震动峰值加速度(Peak Ground Acceleration, PGA)。

重力坝地震易损性分析步骤主要包括：①建立可靠的重力坝地震响应计算模型，选取合理的材料本构模型与参数；②根据地震危险性分析结果，选择与坝址地质条件、坝址地震烈度要求相匹配的系列地震波，并进行标准化处理；③对结构进行非线性地震响应分析，文中采用了非线性动力时程分析方法；④选定易损性性能指标，定义指标相关的结构震害等级标准；⑤对计算的结果数据进行回归处理，建立概率需求模型(Probabilistic Seismic Demand Model, PSDM)；⑥计算结构在各级地震下超越不同性能水准的可能性，给出重力坝的地震易损性曲线。

2 重力坝地震响应计算模型与参数

2.1 计算模型

越南某碾压混凝土重力坝设计方案，最大坝高40.50 m，坝顶高程620.50 m。上游设计水位618.00 m，淤沙高程596.35 m，下游设计水位588.06 m。坝体混凝土采用“金包银”形式，主体采用C10混凝土，部分区域采用C15混凝土，静态抗压强度分别为10 MPa和15 MPa，静弹模分别为17.5 GPa和22 GPa，泊松比为0.2，密度为2 400 kg/m3和2 800 kg/m3。静态抗拉强度按照水工建筑抗震设计规范取静态抗压强度的10%，动弹性模量和动强度在对应静参数基础上提高30%[26]。地基主体为玄武岩、砂岩夹泥岩，等效动弹性模量为16.5 GPa，泊松比为0.25，密度为2 400 kg/m3，通过文献[27]可得，在三倍设计地震以内阻尼比取值为取5%，大于三倍设计地震时阻尼按照5%～8%梯度变化取值，V30剪切波速介于500～1 500 m/s。地震危险性分析的大坝设计地震波加速度峰值为0.11g，考虑浅源近震。

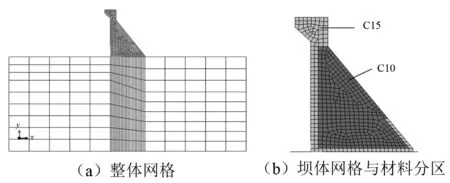
图1 重力坝有限元计算模型Fig.1 Calculationmodel for finite elementanalysis of the gravity dam

2.2 混凝土弹塑性损伤本构模型与参数

坝体混凝土采用弹塑性损伤模型，如图2(a)所示。弹塑性应力应变关系按照混凝土设计规范选取，混凝土受压采用线弹性本构，受拉达抗拉强度前也采用线弹性本构，达抗拉强度后本构为[28]

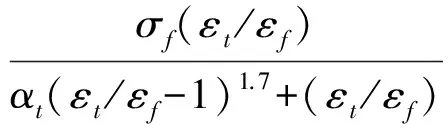
(2)

式中：σt和εt分别为混凝土应力和与之对应的应变；σf和εf分别是混凝土抗拉强度和与之对应的应变；αt为规范中已有的与混凝土强度变化有关的参数，取值见规范。

损伤因子dt与弹塑性损伤模型中的开裂应变关系采用文献[29-30]的公式

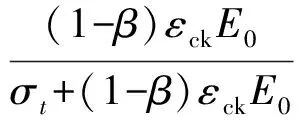
(3)

式中：dt为拉伸损伤系数；β按文献范围选取0.7；E0为初始弹模；εck为开裂应变。

根据式(2)和式(3)可得如图2(a)损伤模型的弹性应变和塑性应变为

(4)

式中，εel和εpl分别为损伤模型中的弹性应变和塑性应变。文中C15和C10混凝土材料的弹塑性损伤本构关系、损伤因子与εck关系如图2(b)所示。

3 地震波的选取与标准化

(a)混凝土弹塑性损伤本构模型

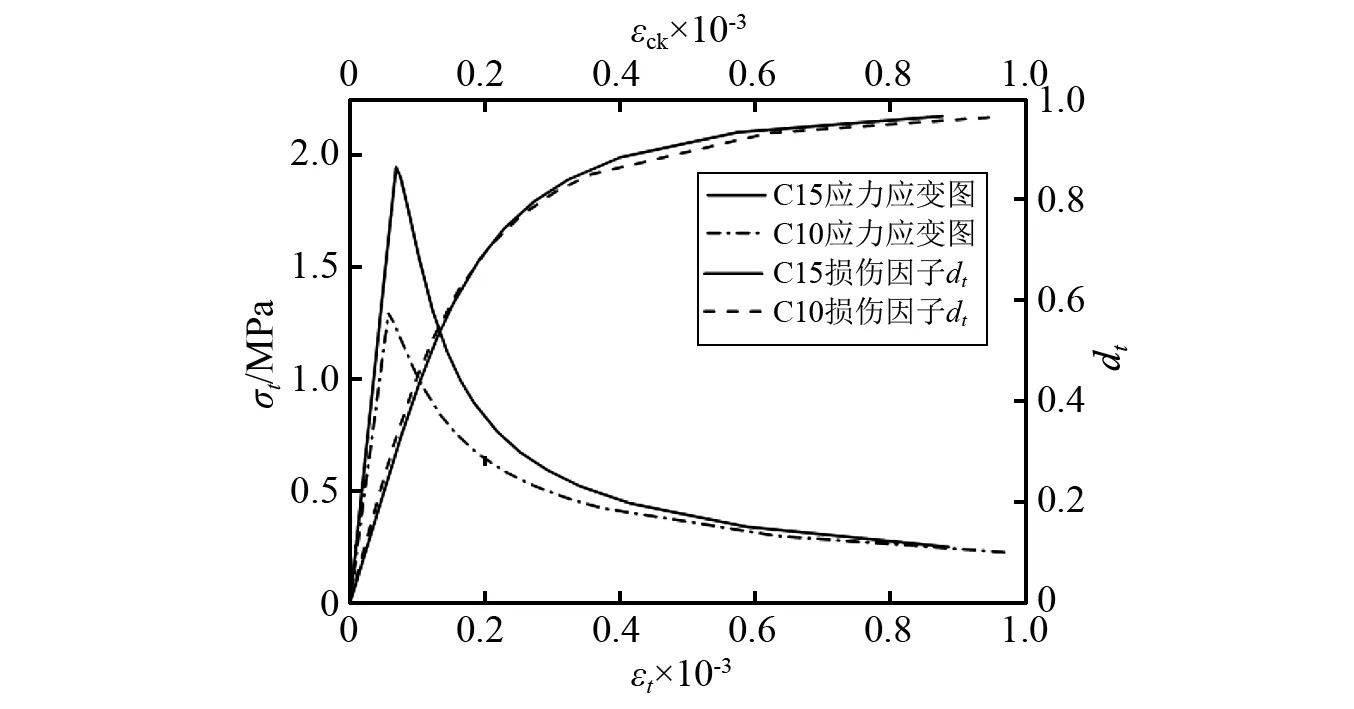
(b)材料参数与损伤因子图2 混凝土弹塑性损伤本构模型和损伤因子Fig.2 Elastic plastic damage constitutive model and damage index

考虑地震作用的不确定性，应该选择符合要求的不同类型地震波。为满足地震危险性分析要求的近震、浅源地震条件，且同时要满足与坝址相近岩石条件，选用表1中的12条地震波，其中震级M为5.0～7.5级，震中距(EpiD)为6.50～50.00 km，V30为500～1 500 m/s。图3给出了前两条地震波的加速度时程曲线。

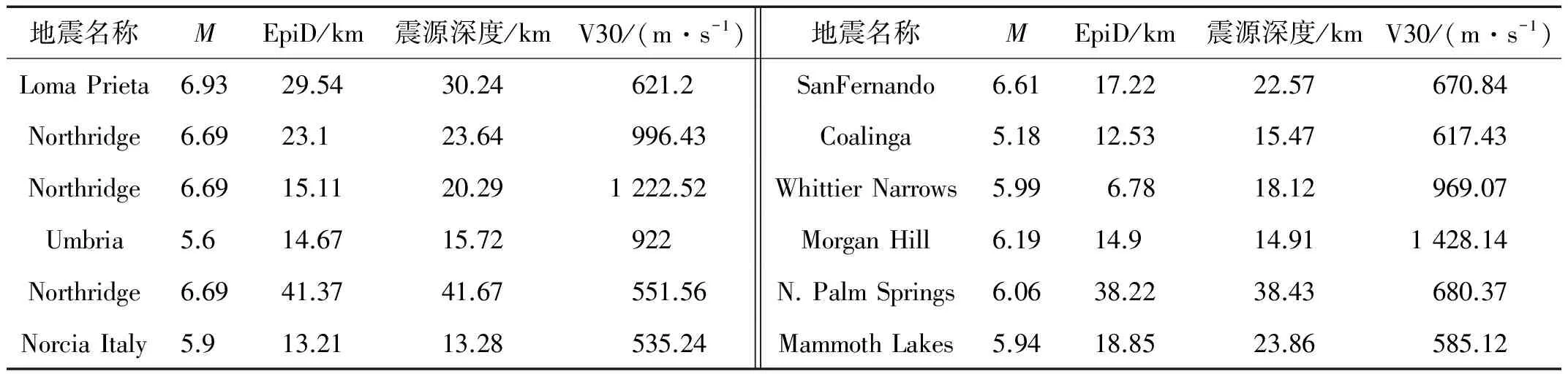
表1 重力坝地震易损性分析的地震记录

图3 前两条地震加速度时程曲线Fig.3 Acceleration time history curveof the first two earthquakes

图4为各条地震波在阻尼比为5%时的放大系数反应谱，其中黑虚线为上述地震波反应谱的平均值，黑粗线是基于抗震设计规范的规范反应谱。由图4可知，12条地震记录反应谱的平均值与规范谱值基本一致，能较好地应用于重力坝易损性分析中。

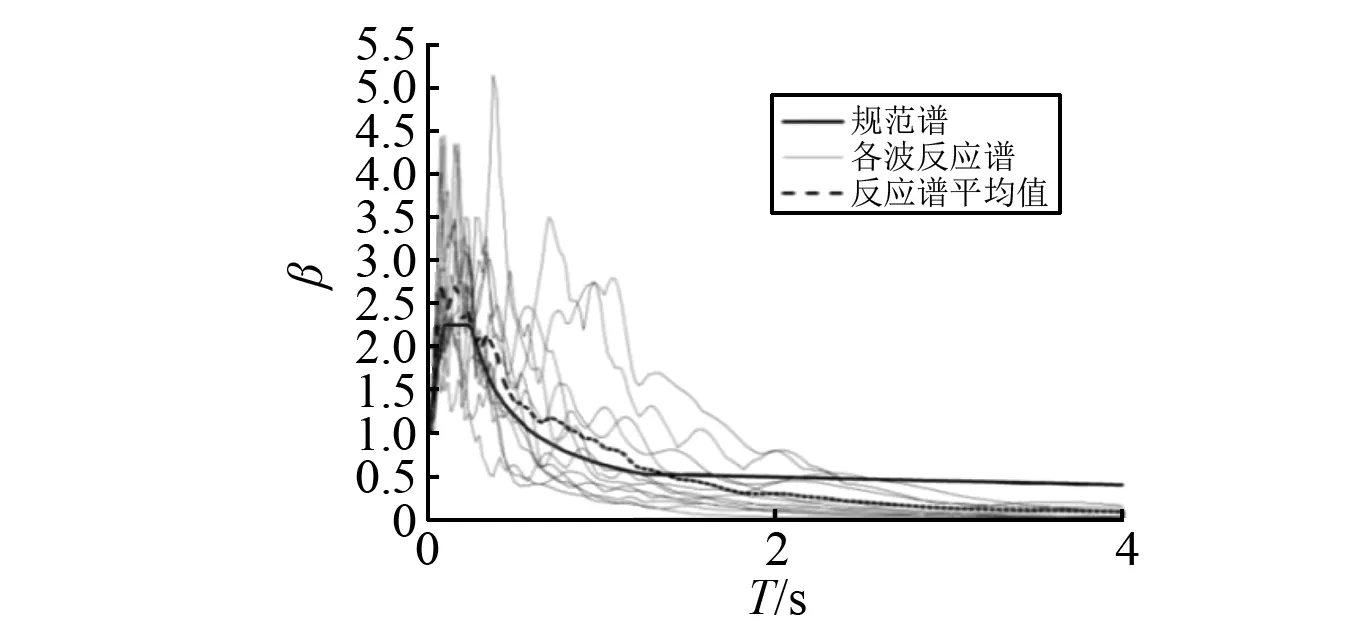
图4 地震波的放大系数谱Fig.4 Amplification coefficient spectrum of seismic waves

以这12条地震记录为依据，根据每条波的PGA进行不同水平的标准化，得到了PGA范围为1～8 m/s2的96条地震波，进行重力坝的非线性动力响应分析。

4 重力坝性能指标的选择和震害等级划分

重力坝在各级地震作用下出现损伤状态也是有差别的。易损性分析需确定各级地震作用下的震害等级划分标准，即位移性能水准LS的值。根据以往震害调查及试验分析，将混凝土大坝在遭受地震荷载作用时可能产生的损伤破坏状态分为五个级别，即基本完好、轻微损伤、中等损伤、严重损伤、溃坝，详细定义如表2所示。

表2 震害等级定义

地震作用下重力坝将在振动过程中产生局部、整体的损伤及裂缝[31]，表现出结构刚度和强度不断退化，导致坝体位移不断增加，该过程中有一些共性的坝体损伤破坏形态，并且这些损伤破坏形态与坝体位移间存在着机理性的联系，可考虑采用位移作性能指标来反映坝体破坏形态，为坝体易损性分析提供定量依据。因此，本文选取两个位移指标作为易损性分析的性能指标：反映结构破坏形态的坝顶上游面顺河向位移(简称为RDCD)；同时考虑到溃坝阶段坝顶顺河向位移衡量可能失效，选取坝颈顺河向位移作为溃坝阶段的补充性能指标(简称为RDND)。

将上述12条输入地震波以其PGA进行不同水平标准化，经过IDA非线性动力时程分析得到两个位移性能指标与重力坝损伤破坏形态对应关系，针对图1所示的重力坝设计方案，表3中列出了在Loma Prieta(波1)和Northridge(波2)作用下的位移性能指标和损伤破坏形态的对应关系情况。

同时，进一步对IDA分析中坝顶上游面顺河向位移(Dam Crest Displacement, DCD)与损伤(Damage)的相关性作定量分析，定义相关系数为

(5)

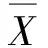
表3 重力坝损伤破坏形态与位移性能指标的对应关系

图5 坝体位移与PGA关系的IDA曲线簇Fig.5 IDA curves of relationship between displacement and PGA

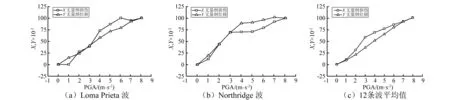
图6 IDA无量纲位移与损伤指数的相关性Fig.6 Correlation of non-dimensional displacement and damage of IDA

图5给出了各地震波作下坝体位移与PGA关系的IDA曲线簇，图6给出了Loma Prieta(波1)、Northridge(波2)和12条波平均值的无量纲位移和损伤指数的相关性情况。

从表3可知，重力坝位移性能指标与的损伤破坏形态存在良好的对应关系，进一步由图6也可见两者间存在强相关性，其中12条地震波的相关性系数介于0.922～0.977，均值为0.974。因此，选取坝顶上游面顺河向位移、坝颈顺河向位移作为易损性分析的性能指标是可行的。同时进行易损性分析时，需要根据性能指标进行震害分级。根据上述位移与损伤的关系，可以通过损伤来进行位移震害等级定量划分。参考重力坝结构响应分析和相应损伤指数的定级方法，文中选用损伤指数震害等级划分标准[32]如表4所示。

表4 基于损伤指数的重力坝震害等级划分标准

由图6损伤与位移的强相关性，确定如下位移震害水准与损伤指数震害水准的关系

(6)

式中：RLSDCD为与损伤指数性能水准限值对应的位移值；LSD为损伤指数的性能水准限值，各级限值如表4所示；LSDCD为根据损伤与位移的强相关性确定的位移性能指标的性能水准限值。

根据表4的LSD和式(6)可得到位移性能指标的性能水准LSDSD，参考Tekie等提供的位移性能水准LS取值，进而确定基于位移指标的重力坝震害等级划分：性能指标介于0%～0.014%H1(LS1)时，坝体基本处于弹性状态，定为一级震害；性能指标介于0.014%～0.035%H1(LS2)时，坝体有轻微损伤，定为二级震害；性能指标介于0.035%～0.105%H1(LS3)时，坝体在坝颈等局部会有中等损伤，定为三级震害；性能指标介于0.105%～0.154%H1(LS4)时，坝体在坝颈及下游面等处有较大面积的严重损伤，定为四级震害；性能指标RDCDgt;0.154%H1(LS4)或RDND大于gt;0.01%H2时，坝体存在大面积损伤，处于溃坝状态，定为五级震害。表5列出了上述五级震害与性能指标关系。

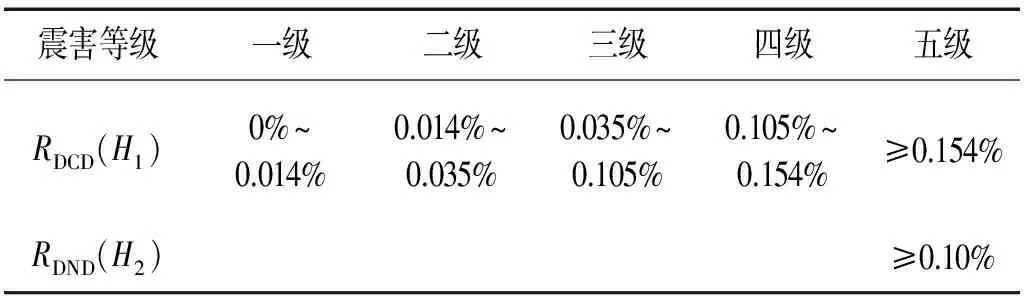
表5 基于位移的重力坝震害等级划分标准

5 重力坝地震易损性分析

5.1 结构反应概率分析

根据SAC-FEMA规范[33-34]，结构性能指标R和地震动参数IM服从指数回归关系

R=a·(IM)b

(7)

式中，a和b为回归系数，可根据线性回归得到。

将式(7)进行对数变换

lnR=b·ln(IM)+ln(a)

(8)

式(7)和式(8)为结构地震动响应参数和地震动指标参数的概率地震需求模型。

根据上述概率地震需求模型，结合图7所示结构性能指标(RDCD和RDND)的非线性动力分析结果，建立两者与地震动参数(PGA)的概率关系，如式(9)所示。

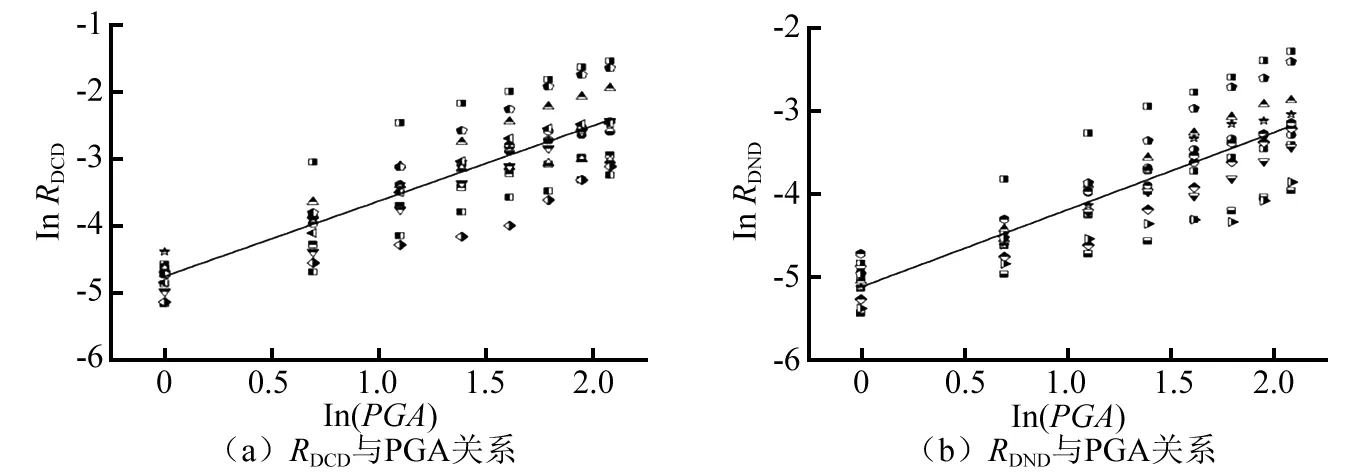
图7 概率地震需求关系模型Fig.7 Probabilistic seismic demand model

lnRDCD=1.127ln(PGA)-4.743

(9a)

lnRDCD=0.922ln(PGA)-5.112

(9b)

RDCD和RDND对IM(PGA)的离散程度，可采用其对数标准差β，其计算公式为

(10a)

(10b)

式中：N为结构响应样本的个数；df为自由度。

5.2 易损性分析结果

在概率地震需求模型的基础上，根据不同的震害等级划分及其相应的性能水准(LS)，可以进一步进行结构的地震易损性分析。采用对数正态分布模型表示地震易损性时，结构超过性能水平达到各震害等级的累计概率(即各震害等级的易损性)为

(11)

将式(9)和式(10)代入式(11)得

(12)

式中，Φ为标准正态分布。

将本文非线性动力分析结果代入公式中，得到坝顶位移和坝颈位移易损性曲线，如图8所示。其中，N为完好、S为轻微损伤、M为中等损伤、E为严重损伤、C为溃坝。

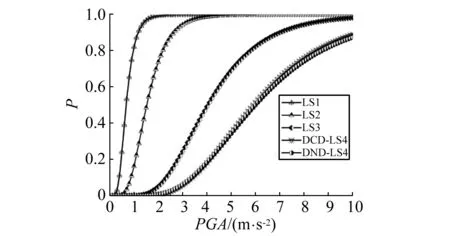
(a) 重力坝易损性曲线

(b) 地震等级易损性柱状图图8 重力坝易损性曲线及柱状图Fig.8 Fragilty curve and histogram of gravity dam

由表5和图8可知，对于该重力坝在正常运行下，如在设计地震0.11g下，坝体中等损伤以上的概率为22.30%，严重损伤以上的概率为0.11%，溃坝为0.004 1%；2倍设计地震时，坝体中等损伤以上的概率为72.67%，严重损伤以上的概率为7.70%，溃坝为1.04%。同时也可见：在严重损伤和溃坝阶段，表征主要位移性能指标RDCD和补充指标坝颈位移RDND与主要位移性能指标的易损性曲线基本一致，表明本重力坝两个指标均能较一致地反映坝体的严重损伤和溃坝状态，相互验证了性能指标选取的合理性。此外可见，该重力坝设计方案由于坝头设计相对过大显著加剧了坝头质量和应力集中，同时坝体混凝土标号整体相对偏低，使得坝体在PGA较小的地震动下坝体也发生了较大损伤和位移，为此建议以减小坝头及应力集中为目标调整该重力坝剖面设计方案，同时适当提高坝体混凝土标号等措施，减小地震作用下损伤破坏概率。

6 结 论

(1)选取坝顶和坝颈相对坝踵的顺河向位移作为抗震性能指标，研究确定了性能指标与破坏形态、结构损伤之间的对应关系，给出了五级震害划分标准及相应的性能水准。

(2)结合SAC-FEMA的概率分析模型，建立了基于位移的重力坝地震易损性分析方法，可计算重力坝在各个水平地震作用下发生各级震害的概率，为重力坝结构抗震设计提供科学参考。

(3)研究表明，重力坝剖面设计中需避免坝头设计相对过大显著加剧坝头质量和应力集中的问题，同时需避免混凝土标号偏低不利于抗震的设计方案，以充分发挥重力坝的良好抗震能力，有效减小地震损伤破坏概率。

[ 1 ] 周建平,杨泽艳,陈观福. 我国高坝建设的现状和面临的挑战[J]. 水利学报, 2006, 37(12): 1433-1438.

ZHOU Jianping,YANG Zeyan,CHEN Guanfu. Status and challenges of high dam constructions in China[J].Journal of Water Resources Engineering,2006, 37(12): 1433-1438.

[ 2 ] ICOLD committee on seismic aspects of dam design. Reservoir triggered seismicity-state of knowledge[C]∥ The 74th Annual Meeting of International Commission on Large Dams. Paris: ICOLD, 2006.

[ 3 ] 陈厚群,徐泽平,李敏. 汶川大地震和大坝抗震安全[J]. 水利学报, 2008, 39(10): 1158-1167.

CHEN Houqun, XU Zeping, LEI Min. Wenchuan earthquake and seismic safety of large dams [J].Journal of Water Resources Engineering, 2008, 39(10): 1158-1167.

[ 4 ] HUANG J J, ZERVAB A. Earthquake performance assessment of concrete gravity dams subjected to spatially varying seismic ground motions[J]. Structure and Infrastructure Engineering, 2014, 10(8): 1011-1026.

[ 5 ] ABDELHAMID H, MAHMOUD B, HUSSEIN M. Seismic fragility and uncertainty analysis of concrete gravity damsunder near-fault ground motions[J]. Civil and Environmental Research, 2013, 5(11): 27-30.

[ 6 ] 钟红, 李晓燕, 林皋. 基于破坏形态的重力坝地震易损性研究[J]. 大连理工大学学报, 2012, 52(1): 60-65.

ZHONG Hong, LI Xiaoyan, LIN Gao. Analyses of failure modes-based seismic fragility of gravity dams [J].Journal of Dalian University of Technology,2012, 52(1): 60-65.

[ 7 ] 沈怀至, 金峰, 张楚汉. 基于性能的重力坝-地基系统地震易损性分析[J]. 工程力学, 2008, 25(12): 60-65.

SHEN Huaizhi, JIN Feng, ZHANG Chuhan. Erformance-based seismic fragility analysis of concrete gravity-foundation system [J]. Engineering Mechanics,2008, 25(12): 60-65.

[ 8 ] TEKIE P B, ELLINGWOOD B R. Seismic fragility assessment of concrete gravity dams[J]. Earthquake Engineering and Structural Dynamics, 2003, 32(14): 2221-2240.

[ 9 ] 陶能付, 夏颂佑. 大坝的地震灾害损失预测研究[J]. 河海大学学报(自然科学版), 1998, 26(1): 88-92.

TAO Nengfu, XIA Songyou. Assessment of earthquake-induced losses of dams[J].Journal of Hohai University (Natural Science),1998, 26(1): 88-92.

[10] 谢礼立, 马玉宏, 翟长海. 基于性态的抗震设防与设计地震动[M]. 北京：科学出版社, 2009.

[11] 周奎, 李伟, 余金鑫. 地震易损性分析方法研究综述[J]. 地震工程与工程振动, 2011, 31(1): 106-113.

ZHOU Kui, LI Wei, YU Jinxin. Review of seismic fragility analysis methods[J].Journal of Earthquake Engineering and Engineering Vibration,2011, 31(1): 106-113.

[12] 姚霄雯, 蒋建群, 刘国华. 基于拱冠位移的拱坝地震易损性[J]. 浙江大学学报(工学版), 2013, 47(10): 1839-1845.

YAO Xiaowen, JIANG Jianqun, LIU Guohua. Deformation-based seismic fragility analysis of concrete arch dams [J].Journal of Zhejiang University (Engineering Science),2013, 47(10): 1839-1845.

[13] 王笃波,刘汉龙,于陶, 等. 基于变形的土石坝地震易损性分析[J].岩土工程学报, 2013, 35(5):1479-1484.

WANG Dubo, LIU Hanlong, YU Tao, et al. Seismic fragility analysis for earth-rockfill dams based on deformation[J].Chinese Journal of Geotechnical Engineering,2013, 35(5): 1479-1484.

[14] ELLINGWOOD B R, TEKIE P B. Fragility analysis of concrete gravity dams [J]. Journal of Infrastructure Systems, 2001, 7(2):41-48.

[15] 李晓燕, 钟红, 林皋. 地震作用下混凝土重力坝破坏过程与破坏形态数值仿真[J]. 水利学报, 2011, 42(10): 1209-1217.

LI Xiaoyan, ZHONG Hong, LIN Gao. Numerical simulation of damage process and failure modesof concrete gravity dams due to earthquakes[J].Journal of Water Resources Engineering,2011, 42(10): 1209-1217.

[16] 沈怀至,张楚汉, 寇立夯. 基于功能的混凝土重力坝地震破坏评价模型[J].清华大学学报(自然科学版), 2007, 47(12): 86-91.

SHEN Huaizhi, ZHANG Chuhan, KOU Lihang. Performance-based seismic damageassessment model for concrete gravitydams [J]. Journal Tsinghua University (Natural Science), 2007, 47(12): 86-91.

[17] 王超, 张社荣, 黎曼, 等. 基于损伤指数模型的重力坝地震破坏等级划分[J]. 地震工程与工程振动, 2014,34 (6): 218-226.

WANG Chao, ZHANG Sherong, LI Man, et al. Classification of earthquake damage to gravity dams basedon a damage index model[J].Journal of Earthquake Engineering and Engineering Vibration, 2014,34 (6): 218-226.

[18] 范书立, 陈健云, 郭建业. 有限元等效应力法在重力坝强度分析中的应用[J]. 水利学报, 2007, 38(6): 754-759.

FAN Shuli, CHEN Jianyun, GUO Jianye. Application of finite element equivalent stress method to analyze the strength of gravity dam[J].Journal of Water Resources Engineering,2007, 38(6): 754-759.

[19] 彭杰, 李同春, 李凌霞. 设计地震作用下拱坝的等效应力应用研究[J]. 水利水电技术, 2015, 46(4): 50-54.

PENG Jie, LI Tongchun, LI Lingxia. Research on application of arch dam equivalent stress under effect of design earthquake[J].Journal of Water Resources Engineering and Hydropower Engineering,2015, 46(4): 50-54.

[20] 刘晶波, 刘阳冰, 闫秋实, 等. 基于性能的方钢管混凝土框架结构地震易损性分析[J]. 土木工程学报, 2010, 43(2): 39-47.

LIU Jingbo, LIU Yangbing, YAN Qiushi, et al. Performance-based seismic fragility analysis of CFST frame structures[J]. China Civil Engineering Journal,2010, 43(2): 39-47.

[21] 赵桂峰, 马玉宏, 陈小飞. 村镇建筑基于性态标准的地震易损性分析 [J]. 土木工程学报, 2014, 47(9): 1-8.

ZHAO Guifeng, MA Yuhong, CHEN Xiaofei. Vulnerability analysis of performance-based seismic design criteria for rural buidings [J]. China Civil Engineering Journal,2014,47(9): 1-8.

[22] 屠冰冰. 基于变形和能量的双参数损伤模型 [J]. 振动与冲击, 2016, 35(11): 196-202.

TU Bingbing. A new two-parameter damage model based on deformation and energy [J].Journal of Vibration and Shock, 2016, 35(11):196-202.

[23] 季昀, 李同春, 姚俊琪. 基于性能的重力坝设计指标选择[J]. 中国农村水利水电, 2013 (2): 85-88.

JI Yun, LI Tongchun, YAO Junqi. Research on performance index applied in gravity dam design based on PBSD [J]. Journal of China Rural Water and Hydropower, 2013(2):85-88.

[24] PEROTTII F, DOMANESCHI M, DE G S. The numerical computation of seismic fragility of base-isolated nuclear power plants buildings[J]. Nuclear Engineering and Design, 2013, 262: 189-200.

[25] 张云, 谭平, 郑建勋, 等. 柱式柔性墩隔震梁桥结构地震易损性分析[J]. 振动与冲击, 2015, 34(16): 48-54.

ZHANG Yun, TAN Ping, ZHENG Jianxun, et al.Seismic fragility analysis on isolated bridges with flexible column piers [J].Journal of Vibration and Shock,2015, 34(16): 48-54.

[26] 水工建筑物抗震设计规范：DL 5073—2000[S]. 北京： 中国电力出版社, 2001.

[27] 林皋. 混凝土大坝抗震安全评价的发展趋向[J]. 防灾减灾工程学报, 2006, 26(1):1-12.

LIN Gao. Developing tendency of the seismic safety evaluation of large concret dams [J].Journa of Disaster Prevention and Mitigation Engineering,2006, 26(1): 1-12.

[28] 混凝土结构设计规范： GB 50010—2010[S]. 北京:中国建筑工业出版社, 2011.

[29] LUBLINER J, OLIVER J. A plastic-damage model for concrete[J].International Journal of Solids and Structure,1989,25(3):229-326.

[30] 张劲, 王庆扬, 胡守营, 等 ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008, 38 (8): 127-130.

ZHANG Jin, WANG Qingyang, HU Shouying,et al. Parameters verification of concrete damaged plastic model of ABAQUS [J].Journal of Building Structure, 2008, 38 (8): 127-130.

[31] 范书立, 陈明阳, 陈建云, 等. 基于能量耗散碾压混凝土重力坝地震损伤分析 [J]. 振动与冲击, 2011, 30(4): 271-275.

FAN Shuli, CHEN Mingyang, CHEN Jianyun, et al. Seismic damage analysis of a concrete gravity dam based on energy dissipation [J].Journal of Vibration and Shock,2011, 30(4): 271-275.

[32] 马智勇. 基于损伤和位移的重力坝地震易损性分析研究[D].南宁： 广西大学, 2016.

[33] Federal Emergency Management Agency.Recommended seismic design criteria for new steel moment-frame buildings:FEMA350[R].Washington: FEMA,2000.

[34] CORNELL C A， JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002,128(4):526-533.

Adeformation-basedmethodforseismicfragilityanalysisofgravitydam

MA Zhiyong1,2, ZHANG Wei1,2, ZHOU Qiang1,2, TANG Keren1,2

(1. School of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China; 2. Key Laboratory of Disaster Prevention and Structural Safetyat Civil Engineering and Architecture, Guangxi University, Nanning 530004, China)

In order to solve the problems of parameter sensitivity of seismic performance indexes, and the difficulty to obtain these indexes and quantitatively determine the grade of seismic damage for gravity dam, a method for fragility analysis of gravity dam based on deformation performance index and the classification of the corresponding seismic damage level were proposed. The horizontal deformations along the river at dam crest and neck relative to heel were both selected as the performance indexes. The correlation between the deformations and failure modes as well as the damage conditions was investigated by using reasonable seismic waves to perform nonlinear dynamic time history analyses. A five-level classification standard of seismic damage was proposed. The procedures for deformation-based seismic fragility analysis were presented by introducing the probabilistic analysis method in SAC-FEMA. The procedures can be employed to guide the design and evaluate the failure probability of gravity dams, and provide basic information on hazard prediction and risk analysis.

gravity dam; seismic fragility analysis; deformation-based; performance index; classification of seismic damage

国家自然科学基金项目(51469004); 广西十百千人才基金项目(2014202)

2016-06-13 修改稿收到日期： 2016-08-09

马智勇 男，硕士，1987年生

张伟 男，博士，教授，博士生导师，1977年生

TV312

A

10.13465/j.cnki.jvs.2017.22.009