混凝土重力坝结构断面优化设计研究
2020-08-17韩继阳杜传阳
韩继阳 ,韩 康 ,杜传阳
(1.莒县水利局,山东 莒县 276500;2.德州市李家岸灌区管理局,山东 德州 253000;3.济南市市政工程设计研究院(集团)有限责任公司,山东 济南250000)
0 引言
重力坝断面基本呈三角形,筑坝材料大多数为混凝土,这种坝称为传统的重力坝。据统计,在各国修建的大坝中,因传统重力坝具有安全性高、耐久性和抗渗性好,设计、施工技术简单,对不同的地形和地质条件适应性强等优点,在各种坝型中往往占有较大的比重。但同时也具有坝体应力较低,坝体体积大,耗用材料多等缺点。因此,从安全性、经济性和美观性出发,对传统重力坝断面进行优化设计尤为重要。本文采用一种新的断面形式为曲线形式的重力坝[1]。本文以新建某枢纽工程重力坝为例,借助ANSYS软件建立数学模型,求解优化设计变量,对优化结果进行分析;对曲线形式重力坝进行应力和抗滑稳定分析,并与传统三角形断面重力坝优化结果进行对比[2]。
1 数学模型的建立
1.1 设计变量
根据传统重力坝与优化后重力坝横断面形式的不同,得到重力坝不同设计变量,传统的重力坝根据其断面形式需要取5个设计变量,即x1~x5,分别表示重力坝断面的不同位置,优化后的重力坝断面为曲面形式,设计中我们将重力坝断面曲线拟定为y=ax2+bx+c的二次抛物线形式,选取上下游曲线方程系数a1,b1,a2作为本文模型设计变量[3]。两种重力坝坝体断面形式见图1。
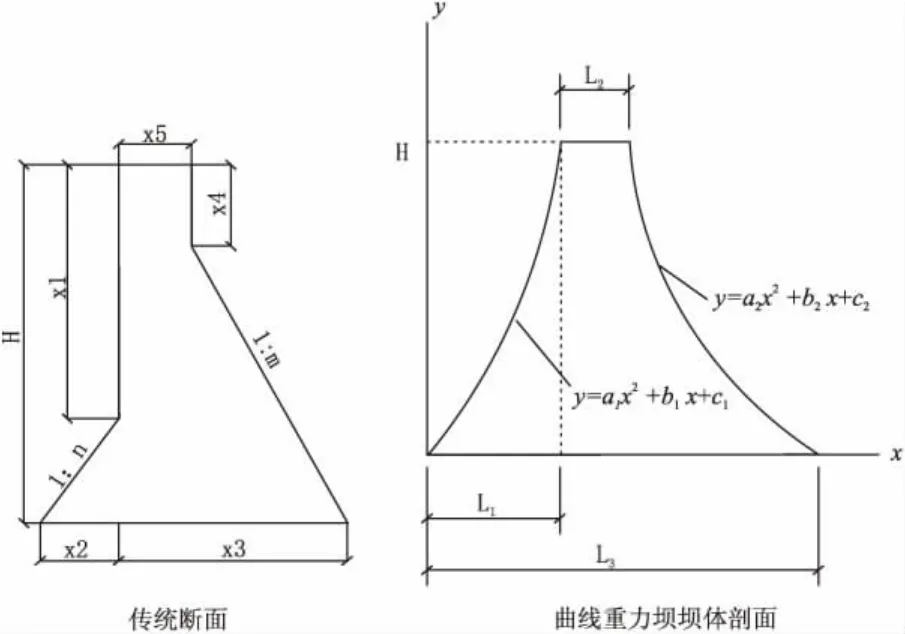
图1 两种重力坝体断面形式
1.2 设计函数
(1)目标函数
本次设计主要是在满足自重和抗滑稳定的情况下确定目标函数为求重力坝设计最小断面A(x),即求minA(x),从而达到经济、节省投资的效果。
(2)约束条件
本文建立目标函数,必须满足以下约束条件:
几何约束:a1>0,a2>0,a2≧0;

式中:Ks为抗滑稳定安全系数;f为抗滑稳定摩擦系数,取值区间0.5~0.8;ΣW为坝体所有荷载在竖向的分力总和,kN;ΣP为坝体上全所有荷载沿滑动面的分力总和,kN;U为坝体所受扬压力,kN。
应力约束:

式中:σyu为坝踵处的竖向应力,MPa;ΣM为荷载对该截面形心的力矩总和,kN·m;MW、MU、Mpy分别为重力、扬压力以及竖向分力对于计算截面形心处的力矩,kN·m;T为计算截面沿上下游方向的宽度,m;σu为坝体的上游边缘处竖向应力,MPa。
1.3 曲线重力坝参数化建模
本文是通过大型有限元计算软件ANSYS软件进行重力坝断面优化设计[4],采用二维平面进行建模求解,得到有限元计算模型。
(1)参数设置
坝面曲线方程系数取值为:a1=1.1,b1=0.8和a2=0.5,γ为水的容重,扬压力折减系数α取值0.2;抗滑稳定摩擦系数f取值为坝踵距坝顶距离为坝底宽度[5]。
(2)单元类型和材料属性
本文中,对混凝土而言,弹性模量E=2.85×104MPa,密度ρ=2400 kg/m3,泊松比 ν=0.167;对基岩而言,弹性模量E=2.00×104MPa,密度 ρ=2600 kg/m3,泊松比 ν=0.300。坝体混凝土,本文采用PLANE82结构实体单元,模型的基岩部分,本文采用PLANE183结构实体单元,基岩范围取上游1.5H,下游2H,坝基深为2H,曲线重力坝有限元网格划分见图2、图3。
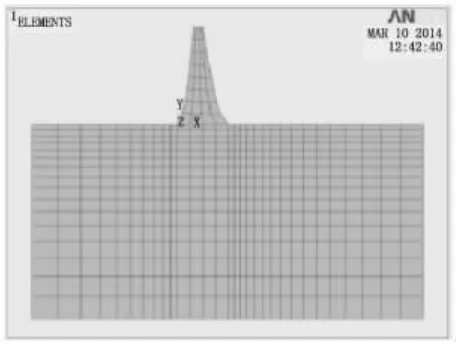
图2 有限元模型网格划分图

图3 曲线重力坝优化模型
(3)约束与加载
在建立有限元模型时,沿坝体轴线的方向取x轴方向,沿重力坝坝体上、下游面上取y方向,建立坐标系,在重力坝坝基底面位置按照固定约束处理,在重力坝坝体上、下游面上(y方向)按照简支约束设置,沿坝体坝轴线的方向(x方向)按简支约束进行处理,为简化计算模型,重力坝其他边界以自由边界进行考虑。
重力坝荷载主要由自重、静水压力、扬压力和地震荷载进行组合加载[6]。在ANSYS中,常规重力坝和优化重力坝在材料参数、计算范围、边界约束条件、单元类型等是相同的。曲线重力坝优化模型图见图3。
2 优化结果分析
本文在ANSYS软件有限元分析时,将零阶分析得到的设计结果做为初值,再通过一阶方法进行更加精确的计算分析[7]。重力坝优化后的设计变量值见表1。

表1 重力坝优化后的设计变量值
2.1 静荷载作用下坝体优化结果分析
静荷载作用下曲线坝体y方向的应力和位移云图见图4。
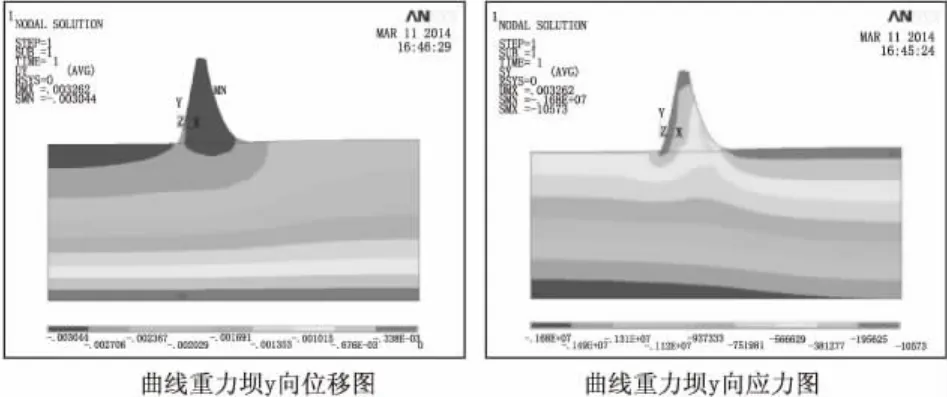
图4 静力荷载作用下曲线重力坝位移和应力云图
由图4可以看出,优化后的重力坝在静荷载作用下,y方向的最大位移发生在坝体上,位移值很小,约3.2 mm,静荷载作用下坝体坝踵位置不会产生拉应力,同时因坝体下游无荷载,坝体的垂直正应力发生在坝体下游基岩上,应力满足设计要求。
2.2 坝体动力分析
动力分析是通过ANSYS对曲线重力坝进行模态分析[8~10],振型图见图5。坝体在完成模态合并后便可得出坝体相应的位移和应力情况。在地震作用下曲线坝体y方向的部分应力和位移云图见图6、图7。
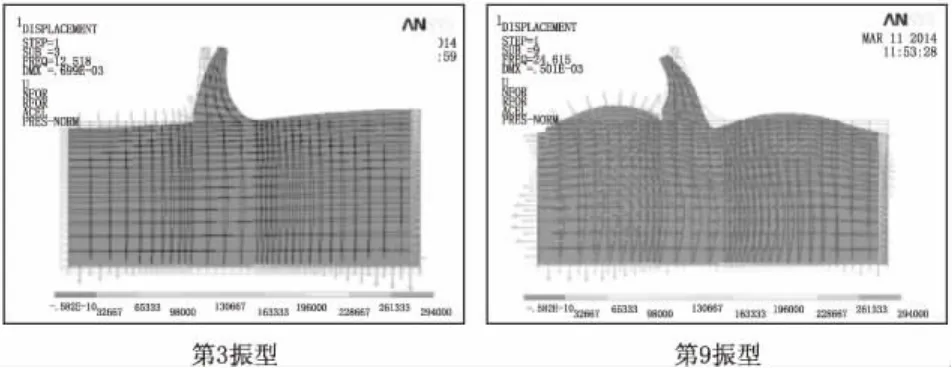
图5 模态分析下各阶振型图(部分)
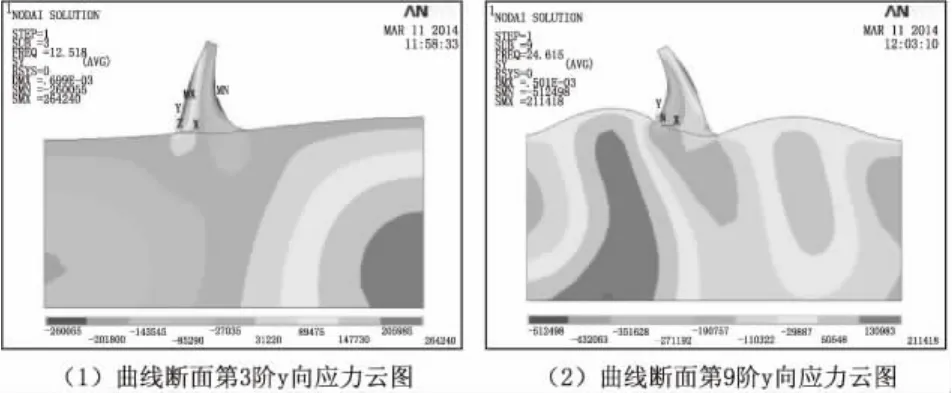
图6 曲线重力坝抗震分析应力云图

图7 曲线重力坝抗震分析位移云图
由图6和图7可知,重力坝在地震荷载作用下坝体的位移和应力都较受静荷载作用时大,位移最大值为4.6 cm,但应力和位移最大值均满足设计要求,最大应力和位移主要发生在基岩上。
2.3 基本断面优化结果
为了更好的体现优化重力设计断面的优越性,对原三角形重力坝断面同样进行了优化设计。优化后的传统剖面图见图8,静力荷载作用下第一主应力云图见图9,传统三角形重力坝断面优化结果见表2。
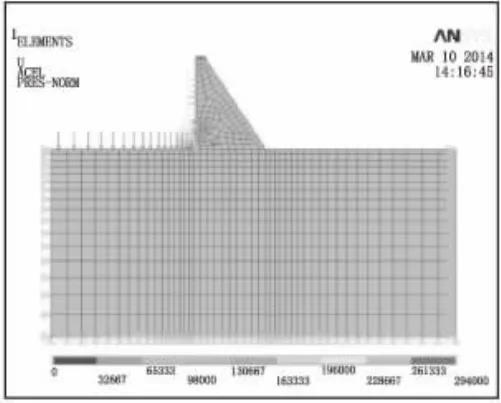
图8 优化后的传统剖面图

图9 静力荷载作用下的第一主应力云图

表2 传统三角型重力坝断面优化结果数据
传统坝面在地震作用下,重力坝的最大位移出现在坝顶位置,其抗震分析的应力、位移云图见图10。由图10可知,坝体的最大应力都发生在基岩上,坝体坝踵处的应力满足要求。

图10 常规重力坝抗震分析应力、位移云图
2.4 断面优化结果对比
运用ANSYS软件,对两种断面进行模拟分析[11],现将相同坝高、相同材料、相同工况下的两种不同断面的结果进行对比,分析结果见表3。
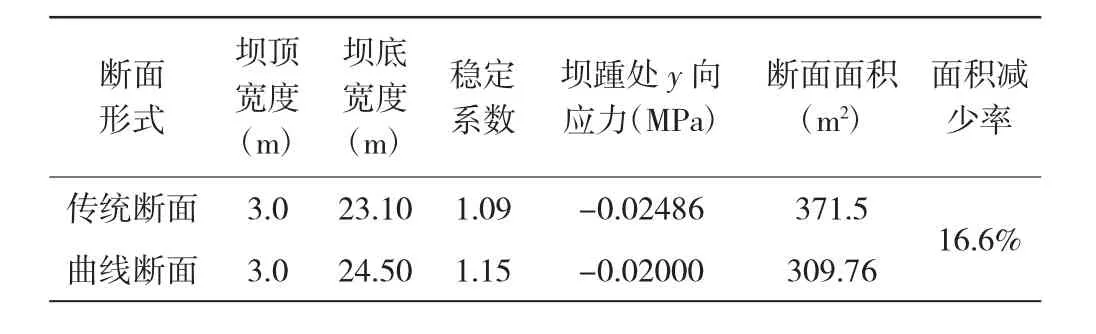
表3 两种坝型优化结果对比表
通过表3两种对比结果可以看出,优化的曲线重力坝明显优于同样优化的三角形重力坝断面,在ANSYS软件经过0阶和1阶优化后,前者较后者在面积上减少16.6%,在经济方面很有优势。
3 结论
本文借助新建小(1)型水库重力坝断面设计,采用ANSYS软件,两种坝型在相同坝高、相同材料、相同荷载情况下,分别进行常规重力坝及曲线重力坝断面优化并进行应力变形分析,得到两种坝型在静荷载和地震荷载作用下坝体应力变形均满足规范要求,但曲线重力坝比基本三角形断面更加节约材料,在经济上占优势;同时与三角形重力坝断面相比,曲线断面的坝底宽度加大而更加有利于坝体稳定。
