模块化多电平换流器排序频率优化设计

高冠伦，李庚银

(1. 国网浙江省电力公司杭州供电公司, 杭州市 310009；2.新能源电力系统国家重点实验室 (华北电力大学)，北京市 102206)

模块化多电平换流器排序频率优化设计

高冠伦1，李庚银2

(1. 国网浙江省电力公司杭州供电公司, 杭州市 310009；2.新能源电力系统国家重点实验室 (华北电力大学)，北京市 102206)

模块化多电平换流器(modular multilevel converter，MMC)因其独特的优势取得了广泛的应用，其中子模块电容电压均衡排序算法成为了热点话题。目前国内外大多数均压算法优化的目的都是为了降低时间计算复杂度和器件的开关频率。通过分析MMC子模块电容电压更新过程和波动原理，推导均压算法的最小排序频率计算方法，通过仿真研究均压算法排序频率对均压效果的影响，根据仿真结果对排序频率进行了优化设计。最后，将厦门柔性直流输电工程作为算例，在PSCAD/EMTDC中搭建模型进行仿真，验证优化设计方案的正确性。由仿真结果可知，论文提出的排序频率优化算法具有较好的均压效果，相比传统的时刻排序方法可以降低器件一半的开关频率，且能同时降低整体平均时间计算复杂度。

模块化多电平换流器(MMC)；最近电平逼近调制；电容电压均衡; 排序算法;开关频率

0 引 言

模块化多电平换流器(modular multilevel converter，MMC)相比于两电平三电平电压源换流器(voltage source converter，VSC)，具有开关频率低、输出电压波形质量好、模块化设计易于扩展等优点，在世界范围内柔性直流输电工程取得了广泛的应用[1-2]。

目前国内外关于MMC的研究主要集中在控制策略[3-4]、建模[5-6]和环流抑制[7]等方面。其中子模块电容电压均衡控制策略是 MMC 应用的关键技术难点。由于换流器桥臂电路损耗、控制环节延时、驱动信号不同步等原因，运行过程中直流侧电容电压会产生不平衡问题。针对该问题，常用的方法可分为实时采集子模块电容电压信息排序与应用载波移相调制技术两大类传统均压算法[8]。文献[9]提出对一个桥臂内部所有电容电压排序，然后根据电流方向选择合适的子模块投入的传统均压策略。文献[8]通过对传统均压策略进行优化，减少子模块开关动作次数，但不适用高电平MMC。文献[10]通过设置子模块电容电压允许偏差值，只在子模块导通个数发生变化时，改变投入的子模块脉冲。但是此策略电压偏差值难以确定，且对开关频率影响较大。文献[11]提出一种快速排序的均压策略，该策略通过检测导通子模块数的变化以及判断各子模块的电容电压是否越界，来决定是否重新计算触发脉冲。此策略过程较为繁琐，但是能够达到同时降低算法的时间计算复杂度和降低器件开关频率的目的，这是目前电容电压均衡发展的方向。

本文通过分析MMC子模块的充放电过程，研究排序算法频率对电容电压均衡的影响，提出一种MMC排序频率优化算法。该优化算法能够有效降低绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)等器件的开关频率，且同时能够降低整体平均时间计算复杂度。最后在PSCAD/EMTDC中搭建仿真模型验证本文算法的正确性。

1 MMC传统均压策略

MMC是德国慕尼黑联邦国防大学的教授Rainer Marquardt在2003年提出的[12]。图1所示为三相MMC的通用结构，共包含6个桥臂，每个桥臂包含n个子模块和1个桥臂电感Larm。文献[3]介绍了MMC的基本运行原理及MMC-HVDC的控制策略。

每个子模块由2个IGBT开关器件，2个反并联二极管和1个直流存储电容构成，并且存在投入、旁路和闭锁3种开关状态。通过2个开关器件T1和T2实现工作状态的切换。通过触发导通上下桥臂不同的子模块数量，使得交流侧输出多电平波形。

在传统电容电压平衡方法中[8-9]，首先监测每个子模块电容电压值，采用冒泡法进行排序。当桥臂电流大于0时，桥臂电流对子模块电容进行充电，根据所需投入的子模块个数按从小到大的顺序投入子模块；当桥臂电流小于0时，桥臂电流对子模块进行放电，根据所需投入的子模块个数按从大到小的顺序投入子模块。

传统的排序算法(冒泡法)具有很好的均压效果，子模块间电容电压值偏差小，但时间复杂度高，子模块投切频繁，故国内外学者对其从不同角度进行了优化改进。目前常用且易于实现的方法是只在子模块开通个数变化的时候对子模块电容电压进行排序，否则不排序。这样能够有效降低器件的开关频率。本文受该方法的启发，在研究MMC子模块电容电压的更新过程后，提出一种MMC排序频率的优化设计方法。

2 MMC子模块电容电压更新

MMC电容电压平衡控制策略的最基本要求是保证每个悬浮的电容电压在额定值附近，避免各个子模块之间的电容电压差值过大导致器件的安全性受到威胁。目前评价电容电压的均衡效果主要是考察子模块电容电压的一致性和电容电压的纹波幅值。此外，IGBT等器件的开关频率和排序均压算法的时间计算复杂度也是评价均压算法优劣的指标之一。

单个子模块投切对于电容电压平衡的调节控制效果和器件开关频率的影响因素，需要从机理上进行深入分析，从而评估各个子模块开关点对整体电容平衡的控制效果[13]。首先研究子模块电容电压的更新过程，子模块的电容电压和流过电容的电流关系为

(1)

(2)

式中：ΔUC是一个周期电容电压的增量；C是子模块电容；iC是流过电容的电流；iarm为桥臂电流。

以厦门柔性直流输电工程的参数为例[14]，子模块电容电压额定值为1 600 V，纹波幅值相对额定值的波动若在 ±(5%～12%)，则最大波动量为128 V。取C=10 mF，周期T=100 μs，桥臂电流最大值iarm_max=1 750 A，由此可以计算出每个周期内子模块电容电压的最大增量为

(3)

由式(3)可以看出，每个周期的子模块电容电压最大增量与子模块额定电容电压1 600 V相比，十分微小，小于电容电压最大波动量160 V的11%。因此，在传统的冒泡排序过程中，没有必要每个仿真步长都进行MMC排序。

减少排序频率的同时既可以减少整体时间复杂度从而减少占用计算机的资源，还能够让IGBT更为持久地保持原有的状态，从而降低器件的开关频率。但是若排序频率过低可能导致子模块电容电压发散，MMC系统电压失去平衡。

3 MMC排序频率优化

3.1 排序频率计算方法

考虑均压算法、数字控制系统延时、电压传感器采样时间以及硬件板卡的固定时钟周期，实际工程控制器的控制周期为100 μs左右，若按照传统的排序方法时刻排序，则排序频率约为

(4)

式中frank是电容电压均衡算法的排序频率。

由第2节分析和式(3)可知，若要求子模块电容电压的纹波幅值不超过工程要求的限制，则每2次排序之间的间隔时间内电容电压的增量不能超过子模块电容电压最大波动量，由此可计算出每2次排序之间的间隔时间：

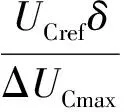
(5)

式中：tgap是电容电压均衡算法的排序时间间隔；UCref是子模块电容电压额定值；δ是子模块纹波幅值相对额定值的波动百分比；ΔUCmax是1个周期电容电压的最大增量；T是1个控制周期。由此可以计算出相应的排序频率。联立式(1)至式(5)可总结出优化的电容电压均压算法最小的排序频率计算公式为

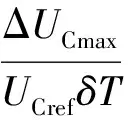
(6)

式中：frank_min是电容电压均衡算法的最小排序频率；iarm_max是稳态时桥臂电流最大值；UCref是子模块电容电压额定值；δ是子模块纹波幅值相对额定值的波动百分比；C是子模块电容。

电磁暂态软件仿真不论在一次系统还是控制器方面都和实际工程有着很大的差别，电磁暂态仿真模型通过每个仿真步长的反复求解去模拟真实器件的电容电压更新过程，故以上的理论推导公式还需通过仿真进一步研究。

3.2 排序频率仿真研究

在电磁暂态软件中，子模块电容电压的更新过程只是在每个仿真步长进行迭代更新，但实际器件是每时每刻都在更新，故电磁暂态的仿真步长不能与实际物理器件的控制周期等价。若式(6)要应用于电磁暂态软件，如PSCAD/EMTDC，则需要通过仿真研究排序频率对均压效果的影响，从而对式(6)进行修正。

因此，本文在PSCAD/EMTDC中根据厦门柔性直流输电工程参数搭建MMC仿真模型[14]，系统接线图如图2所示。分别取仿真步长为40，100 μs进行仿真，研究控制排序频率下的电容电压均衡效果。本文取子模块纹波幅值相对额定值的波动百分比δ=12%。

图2 厦门MMC工程接线图Fig.2 Xiamen MMC project configuration

(1)当仿真步长取40 μs时，若每个仿真步长都排序(时刻排序)，则排序频率frank1=25 000 Hz，若按照式(6)进行计算则排序频率frank2=972 Hz。为了说明排序频率的影响，取2种排序算法下的换流器整流侧正极A相上桥臂中的前10个子模块的电容电压波形进行观测，如图3(a)、(b)所示，子模块电容电压的额定值为1.6 kV。从图3(a)中可以看出，子模块的电容电压的波形重叠度高，一致性很好，纹波幅值约为0.18 kV，不超过12%。但图3(b)的子模块电容电压波形多数不重叠，一致性差，电容电压相比额定值1.6 kV波动太大，最大波动量约为1.1 kV，远远超过12%，将对系统的安全性造成很大威胁。因此，经式(6)计算的排序频率不能直接应用于仿真，这可能是由于PSCAD/EMTDC等电磁暂态仿真软件中的仿真步长与实际控制器周期不等价造成的。本文通过多次仿真发现，在排序频率frank3=5 000 Hz时，子模块均压效果较好，能够满足系统的要求。子模块的电容电压波形如图3(c)所示，各个子模块电容电压波形的贴合程度接近于时刻排序，但波形的整体位置与图3(a)中时刻排序的电容电压相比有一定的偏置，子模块电容电压纹波幅值约为0.19 kV，不超过12%，能够很好地满足MMC系统的均压需求。

本文通过减少排序算法的排序频率，能够尽可能地保持IGBT的状态，从而减少IGBT的开关频率。通过仿真测得不同控制频率下的IGBT的开关频率，如表1所示，时刻排序时IGBT的开关频率约为271 Hz，本文排序频率的优化算法约为135 Hz，可以降低一半的开关频率。尽管继续降低开关频率可以减少器件的开关频率，但是当排序算法的排序频率低于本文优化设计的排序频率值时，均压效果很差，甚至会导致系统电容电压失去平衡。

图3 仿真步长为40 μs时电容电压波形Fig.3 Capacitor voltage waves under different rankingfrequencies while solution step is 40 μs

表1不同排序频率下IGBT的开关频率
Table1SwitchingfrequencyofIGBTunderdifferentrankingfrequencies

(2)当仿真步长取100 μs时，若每个仿真步长都排序(时刻排序)，则排序频率frank4=10 000 Hz，若按照式(6)进行计算则排序频率frank2=972 Hz。在此，也取对应2种排序算法下的换流器整流侧正极A相上桥臂中的前10个子模块的电容电压波形进行观测，如图4(a)、(b)所示。从图4(a)中可以看出，子模块的电容电压的波形重叠度高，一致性很好，纹波幅值与图3(a)中几乎相等，约为0.18 kV，不超过12%。从图4(b)中可以看出，子模块的电容电压的波形重叠度较高，一致性很好，纹波幅值相比图4(a)稍大，与图3(a)相比几乎相等，大约也为0.18 kV，不超过12%。

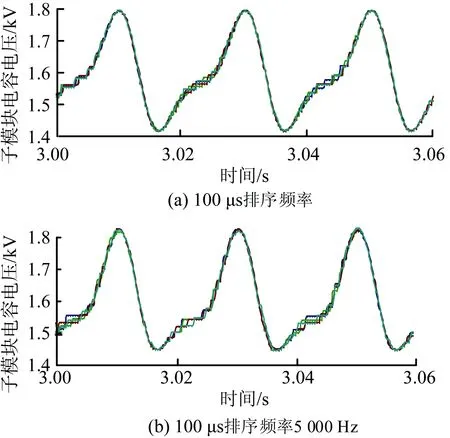
图4 仿真步长为100 μs时电容电压波形Fig.4 Capacitor voltage waves under different rankingfrequencies while solution step is 100 μs

综上，本文优化设计的排序频率frank3=5 000 Hz时，均压效果较好，并且器件的开关频率可以降低一半。此时排序算法时间计算复杂度整体平均值可以降低至传统排序算法的1/5。由此，排序频率的计算公式(6)可以修正为

(7)

4 仿真验证

为了更好地说明本文排序频率优化算法的正确性，对采用式(7)计算的排序频率进行了仿真验证。模型仍采用厦门工程参数，仿真步长为40 μs。

对比采用时刻排序的排序频率frank1=25 000 Hz和采用本文优化排序频率frank3=5 000 Hz的系统特性，取整流侧正极桥臂电压、交流侧电流、正极直流电压和正极输送的有功功率波形进行对比。如图5—8所示。

从图5中2个子图的波形对比可以看出，波形幅值相等，波形几乎一致，由此说明子模块电容电压的微幅波动对桥臂电压影响很小。图6中2个子图中交流电流一致，说明不同的排序频率会对交流侧产生影响。图7中排序频率frank3=5 000 Hz直流电压波形略大一些。图8中2个子图的波形完全一致，本文排序频率优化算法对系统传输的功率没有产生影响。

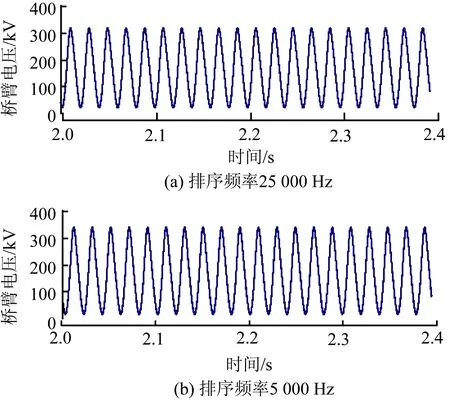
图5 桥臂电压对比Fig.5 Comparison of arm voltages

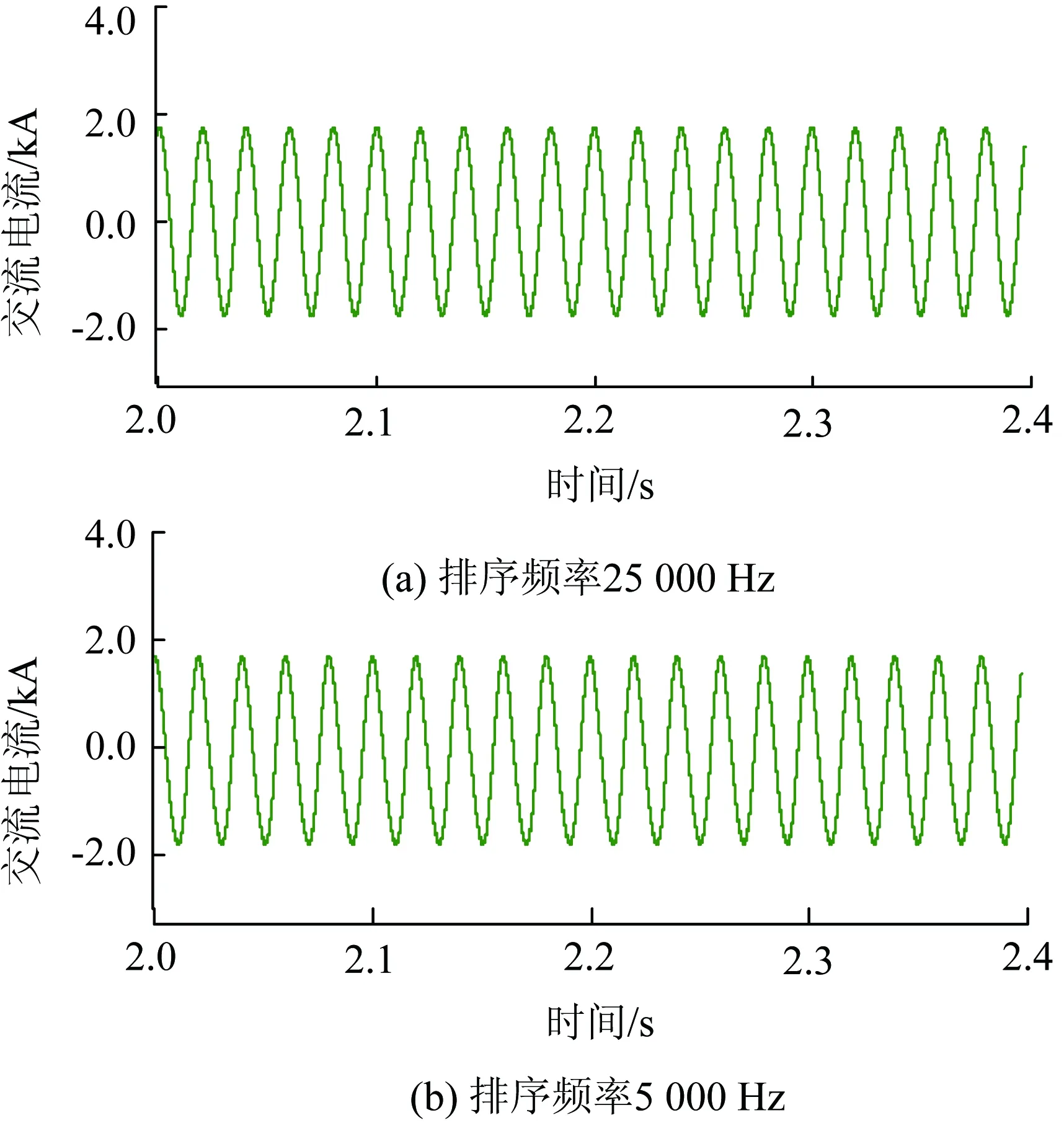
图6 交流电流对比Fig.6 Comparison of AC currents

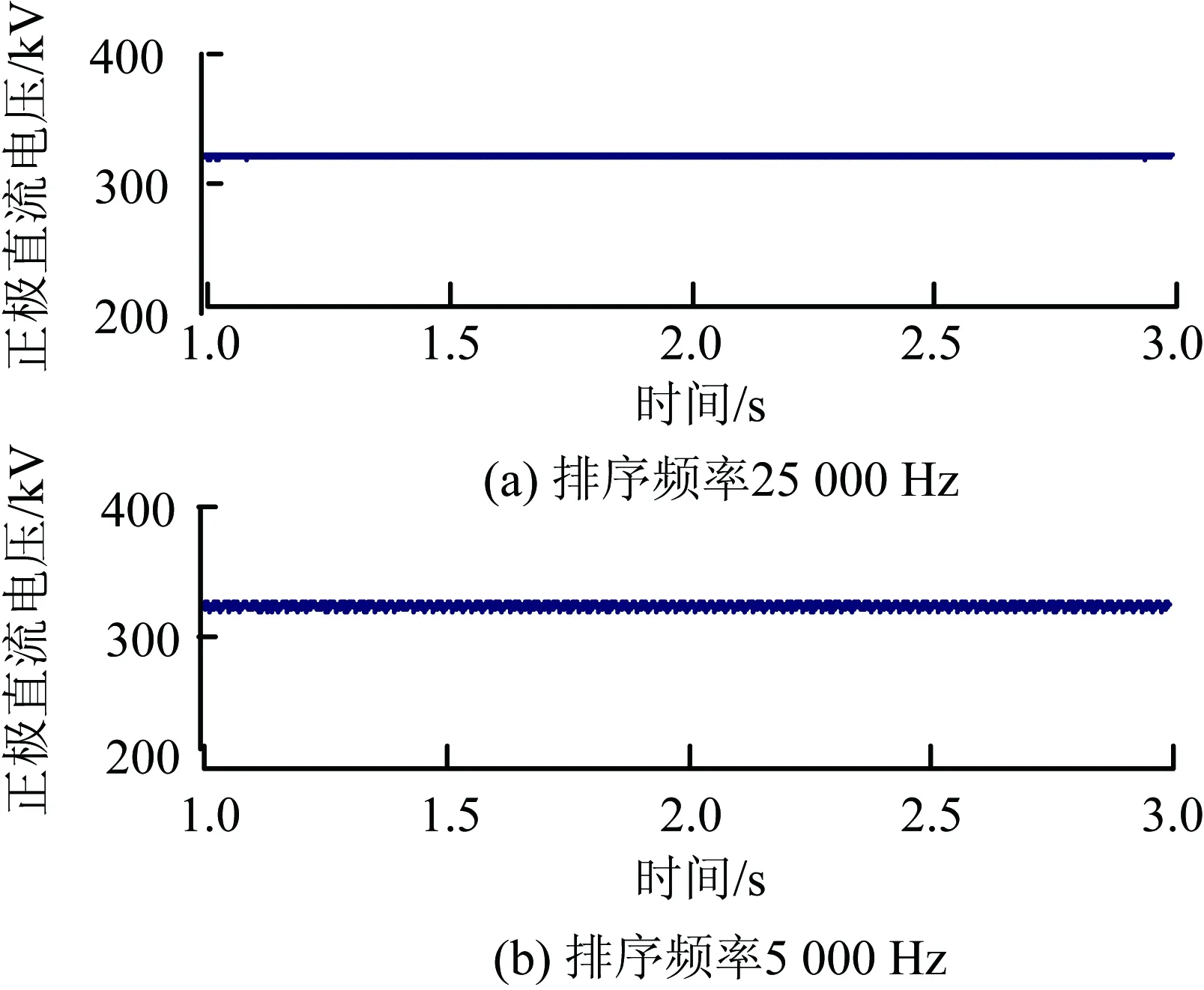
图7 正极直流电压对比Fig.7 Comparison of DC voltages in positive pole

图8 正极输送有功对比Fig.8 Comparison of active power delivered bypositive pole

综上，采用本文提出的MMC电容电压排序频率优化方法，可以实现较好的均压效果，对MMC系统特性几乎没有影响。

5 结 论

目前国内外学者对MMC电容电压均衡算法改进的主要目的是降低IGBT开关频率和排序算法的时间计算复杂度。本文通过研究子模块电容电压的更新过程，研究排序算法的排序频率对电容电压均衡效果的影响，提出了一种MMC排序频率优化算法，推导了均压算法最小的排序频率计算公式。以厦门柔性直流工程为算例在PSCAD/EMTDC搭建模型，验证了本文算法的正确性。本文优化设计的排序频率相比传统的时刻排序方法可以降低一半的器件开关频率，并且能够同时降低时间计算复杂度的整体平均值。但在采用本文优化设计的排序频率时，子模块电容电压会出现小范围的偏置，具体原因还需进一步深入研究。

[1] 汤广福,庞辉,贺之渊. 先进交直流输电技术在中国的发展与应用[J]. 中国电机工程学报,2016,36(7):1760-1771.

TANG Guangfu， PANG Hui， HE Zhiyuan. Ramp;D and application of advanced power transmission technology in China[J]．Proceedings of the CSEE，2016,36(7)：1760-1771．

[2] 韩亮,白小会,陈波, 等. 张北±500kV柔性直流电网换流站控制保护系统设计[J]. 电力建设, 2017, 38(3): 42-47.

HAN Liang, BAI Xiaohui, CHEN Bo, et al . Control and protection system design of Zhangbei ±500 kV converter station in VSC-HVDC power grid[J]. Electric Power Construction, 2017, 38(3): 42-47.

[3] 丁冠军，汤广福，丁明，等．新型多电平电压源换流器模块的拓扑机制与调制策略[J]．中国电机工程学报，2009，29(36)：1-6．

DING Guanjun， TANG Guangfu，DING Ming，et al．Topology mechanism and modulation scheme of a new multilevelvoltage source converter modular[J]．Proceedings of the CSEE，2009，29(36)：1-6．

[4] 管敏渊，徐政．MMC 型VSC-HVDC 系统电容电压的优化平衡控制[J]．中国电机工程学报，2011，31(12)：9-14．

GUAN Minyuan，XU Zheng．Optimized capacitor voltage balancing control for modular multilevel converter based VSC-HVDC system[J]．Proceedings of the CSEE，2011，31(12)：9-14．

[5] SAAD H D，MAHSEREDJIAN S，DELARUE J，et al．Modular multilevel converter models for electromagnetic transients[J]．IEEE Transactions on Power Delivery，2014，29(3)：1481-1489．

[6] 石吉银,唐志军,林国栋, 等. 模块化多电平换流器无环流仿真模型[J]. 电力建设, 2017, 38(3): 27-33.

SHI Jiyin, TANG Zhijun, LIN Guodong, et al. A simulation model without circulating current of modular multilevel converter[J]. Electric Power Construction, 2017, 38(3): 27-33.

[7] TU Q R，XU Z，XU L．Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters[J]．IEEE Transactions on Power Delivery， 2011， 36(3)： 2009- 2017．

[8] 辛业春,王朝斌,李国庆,等. 模块化多电平换流器子模块电容电压平衡改进控制方法[J]. 电网技术,2014,38(5):1291-1296.

XIN Yechun，WANG Chaobin，LI Guoqing，et al．An improved balance control for sub-module capacitor voltage of modular multilevel converter[J]．Power System Technology，2014，38(5)：1291-1296．

[9] 刘钟淇,宋强,刘文华. 基于模块化多电平变流器的轻型直流输电系统[J]. 电力系统自动化,2010,34(2):53-58.

LIU Zhongqi, SONG Qiang，LIU Wenhua．VSC-HVDC system based on modular multilevel converters[J]．Automation of Electric Power System，2010，34(2):53-58．

[10] 屠卿瑞，徐政，郑翔，等．一种优化的模块化多电平换流器电压均衡控制方法[J]．电工技术学报，2011，26(5)：15-20．

TU Qingrui，XU Zheng，ZHENG Xiang，et al．An optimized voltage balancing method for modular multilevel converter[J]．Transactions of China Electrotechnical Society，2011，26(5)：15-20．

[11] 喻锋,王西田,林卫星,等. 一种快速的模块化多电平换流器电压均衡控制策略[J]. 中国电机工程学报,2015,35(4):929-934.

YU Feng, WANG Xitian, LIN Weixing, et al. A fast voltage balancing control method for modular multilevel converter[J]．Proceedings of the CSEE，2015,35(4):929-934.

[12] LESNICAR A，MARQUARDT R．An innovative modular multilevel converter topology suitable for a wide power range[C]//Power Tech Conference Proceedings. Bologna：IEEE，2003．

[13] 姜喜瑞,贺之渊,汤广福,等. 基于禁忌搜索优化算法的高压大容量柔性直流输电子模块电容电压平衡算法[J]. 中国电机工程学报,2013,33(21): 71-80, 195.

JIANG Xirui, HE Zhiyuan, TANG Guangfu, et al. A capacitor voltage balancing control strategy for high-voltage large-capacity VSC-HVDC systems based on tabu search hard optimization algorithm[J]．Proceedings of the CSEE，2013,33(21):71-80, 195.

[14] DING H, WU Y, ZHANG Y, et al. System stability analysis of Xiamen bipolar MMC-HVDC project [C]// 12th IET International Conference on AC and DC Power Transmission. Beijing: 2016: 1-6.

2017-05-05

高冠伦(1982)，男，硕士，工程师，主要研究方向为电力系统分析与控制、柔性直流输电；

李庚银(1964)，男，博士，教授，博导，主要研究方向为新能源电力系统分析与控制、柔性输电技术、电能质量。

(编辑 刘文莹)

OptimalDesignofRankingFrequencyforModularMultilevelConverter

GAO Guanlun1, LI Gengyin2

(1.State Grid Hangzhou Power Supply Company, Hangzhou 310009, China; 2. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)

Modular multilevel converter (MMC) has been widely used due to its typical advantages, and the sort algorithm of voltage capacitor balancing in MMC sub-modules has been a hot issue nowadays. The optimization of most voltage balancing algorithm is mainly aimed to reduce the time and computing complexity and its switching frequency at present. This paper analyzes the renewal process and wave principle of the capacitor voltage in MMC sub-modules, and deduces the calculation method of the minimum ranking frequency of voltage balancing algorithm. The influence of the ranking frequency on the voltage balancing effect is studied by simulation, and the ranking frequency is optimized according to the simulation results. Finally, taking Xiamen Project as an example, this paper constructs the model in PSCAD/EMTDC for simulation, to verify the correctness of the proposed optimized design scheme. The simulation results show that the proposed ranking algorithm optimization algorithm has good voltage balancing effect, which can reduce half of the switching frequency of the device compared with the traditional time sorting method and can reduce the computational complexity of the overall average time at the same time.

modular multilevel converter (MMC); nearest level modulation; voltage capacitor balancing; ranking algorithm; switching frequency

TM77

A

1000-7229(2017)11-0026-06

10.3969/j.issn.1000-7229.2017.11.004