电池储能系统最优容量与合同价格的双层优化规划方法

刘译聪, 牛淑娅，杨洋，刘文霞，李永贤，刘座铭

(1.新能源电力系统国家重点实验室(华北电力大学), 北京市 102206；2.国网天津市电力公司城西供电分公司，天津市 300110；3. 国网宁夏电力公司，银川市 750001；4. 国网吉林省电力有限公司电力科学研究院，长春市 130012)

电池储能系统最优容量与合同价格的双层优化规划方法

刘译聪1, 牛淑娅2，杨洋1，刘文霞1，李永贤3，刘座铭4

(1.新能源电力系统国家重点实验室(华北电力大学), 北京市 102206；2.国网天津市电力公司城西供电分公司，天津市 300110；3. 国网宁夏电力公司，银川市 750001；4. 国网吉林省电力有限公司电力科学研究院，长春市 130012)

电池储能系统因其兼具供蓄能力，已成为电网优化运行的重要调控手段。该文以电池独立运营商在配电网层面投资建设电池储能系统，配电网公司以合同电价形式引导储能充放电策略为应用场景，建立了电池储能系统最优容量与合同价格的双层优化规划模型。针对模型求解过程易陷入局部最优的缺点，对粒子群算法的自适应权重计算公式进行改进并引入Cauchy-Gaussian消减变异因子，对局部最优极值进行扰动调整。以改进IEEE-33节点配电系统为例验证了所提模型的可行性与有效性。

电池储能系统; 合同电价; 最优容量配置; 改进粒子群算法; 双层规划

0 引 言

随着分布式电源的不断发展，间歇性分布式电源规模化接入对电网的负面影响逐步显现。因此，兼具供蓄能力的电池储能系统(battery energy storage system，BESS)需求量大增，成为未来电网优化运行的重要调控手段。但我国储能行业起步晚，技术尚待进一步成熟，储能相关的推动政策仍处在初期发展阶段。2016年6月，国家能源局颁布了《关于促进电储能参与“三北”地区电力辅助服务补偿(市场)机制试点工作的通知》，积极鼓励储能设施建设，包括鼓励发电和售电企业等投资、规划新能源发电基地时配臵、在用户侧建设分布式储能设施等[1]，但仍无对储能的补贴价格与具体的补贴政策进行说明，缺乏明确的补贴机制和具体技术路线，投资回报较低。在目前配置成本高昂的背景下，我国电池储能技术的大规模发展应用受到阻碍。因此，深入挖掘储能接入电力系统的多种潜在经济效益，探讨多种形态的储能投资运行方式，对促进储能发展，推动其实际应用具有重要意义。

目前，国内外针对BESS在配电网中的优化配置已做了广泛研究，并取得了一定的研究成果。文献[2]建立了BESS价值评估模型，并以总经济价值最优为优化目标，建模决策BESS的最佳配置容量。但由于文中BESS的投资主体指代不明，导致计及的多项收益的受益主体相互矛盾。文献[3]以配电网公司净收益最大为目标，建立了考虑运行策略及投资主体利益的BESS优化配置模型，但文献[3]中的各项成本收益分析均以配电网公司为研究主体，将投资主体进行了统一，但仅局限于电网公司。可见，目前大部分已有的研究对投资主体缺乏明确的指代，研究角度较为单一，无法保证多种投资主体利益共赢。因此，本文在文献[3]的基础之上，从不同的应用角度出发，探讨不同投资主体在配电网中配置电池储能系统的优化规划方法，科学合理地对BESS进行优化配置，可使BESS的投资规模扩大，推进其大规模应用。

在我国储能补贴力度不足、经济性低、投资与受益主体不明确的现状下，本文以电池独立运营商在配电网中投资建设电池储能系统为应用场景，提出一种BESS运营商与配电网公司协同规划的电池储能最优容量双层规划方法，将充放电合同电价作为优化变量，在电池储能配置过程中计及配电网公司对BESS的优化调度。上层为配电网经济调度模型，对粒子群算法的自适应权重计算公式进行改进并引入Cauchy-Gaussian消减变异因子，对局部最优极值进行扰动调整；下层模型针对BESS优化配置，采用MATLAB中的YALMIP工具箱求解。上下层决策过程相互反馈，不断循环迭代优化，从而实现BESS运营商与配电网公司同时获利。最后，以改进IEEE-33节点配电系统为例验证所提模型的可行性与有效性。

1 电池储能系统双层规划模型

电池储能运营商与配电网公司协同规划的分级模型结构如图1所示。

图1 分级模型结构示意图Fig.1 Hierarchical model structure diagram

模型中共涉及2个参与主体，配电网公司(distribution company, DISCO)和BESS运营商。作为新的市场参与主体，BESS运营商迫切希望通过储能系统的最优配置获益，但如果DISCO任由BESS任意配置及随意进行充放电，则很大可能会对配电网造成不利影响。因此，DISCO必须参与到BESS的配置过程中，对其运行过程实施干预。

根据文献[4]，该问题属于双层规划模型。本文设定上层模型仿真配电网的经济调度过程，以BESS配置前后DISCO的经济效益差值最大为优化目标，并向BESS运营商提供各时刻充放电的合同电价；下层模型重点解决BESS的优化配置问题，使得BESS运营商的净收益最大，决策BESS的额定容量及额定功率，并根据上层的合同电价优化BESS运行策略，同时将优化后的充放电计划返回上层。上层DISCO根据下层反馈的电池储能充放电功率，重新调整调度过程并修改合同电价。如此循环迭代，直至达到最大迭代次数或上下层决策变量变动小于允许值时结束[5]。

1.1 上层优化模型

传统处理配电网经济调度问题的方法，是将配电网运行成本(包括购电成本、网损成本和环境成本等)最小作为优化目标函数，这种处理方法仅计及了BESS接入带给配电网的直接收益，如削峰填谷、减小网络损耗等，而忽略了其潜在收益，如延缓电网升级改造和在故障过程中的经济效益。基于此，本文在仿真配电网经济调度问题时，以BESS配置前后DISCO的经济效益差最大为优化目标，如下所示：

maxFD=Bdir+Bdel+Benv+Brel

(1)

式中：FD代表BESS配置前后DISCO的经济效益增量；Bdir为直接收益增量；Bdel为延缓电网升级改造获利；Benv为环境效益；Brel为减小停电损失获利。其中，Bdir需计及DISCO向BESS运营商购电的成本和储能系统充电的收益，具体如式(2)所示：

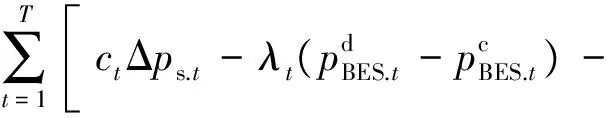
(2)

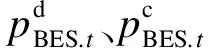
在故障过程中，储能系统服从系统调度，可作为紧急电源向重要用户供电，提高了系统的可靠性，降低了系统的停电损失。因此，储能系统应获得一定激励性质的补偿。此时Brel需计及BESS在故障过程中发挥效用的补偿。Brel的具体表达式如下：

(3)

式中：I为配电网中的重要用户数；EENS.j为重要用户j的年期望缺供电量；Sres为BESS在系统故障时的期望剩余电量；Smin为BESS的最小允许剩余电量；pBIO.j为仅有储能系统和重要用户j位于同一孤岛的概率，即BESS能够在故障时继续为用户j供电的概率；RIEA.j为用户j的单位缺供电量经济损失，元/(kW·h)；cBR为BESS参与紧急需求侧响应的单位支付价格，参考紧急需求侧响应对用户负荷的支付价格，并考虑到国内生产消费水平及经济发展等实际因素，BESS故障过程中服从DISCO调度，参与紧急需求侧响应的支付价格取10美元/(kW·h)[6]；SDG为系统故障期间DG的期望输出；pDBI.j为DG、储能系统和重要用户j同时位于同一孤岛的概率[7]。

上层模型需满足如下约束：

(1)合同电价范围约束。

为缩小最优解的搜索空间，给定各时刻BESS充放电的合同电价上下限范围约束：

0≤λt≤λmax

(4)

式中λmax为合同电价的取值上限。

(2)系统功率平衡约束[8]。

(5)

式中：pDG.n.t为t时刻第n个DG的出力；ps.t为t时刻

系统的总负荷；pls.t表示系统的网络损耗。

(3)节点电压、线路电流约束。

(6)

式中：Vi为节点i处的电压值；Vmin为电压下限；Vmax为电压上限；Iij为节点i与节点j之间线路上的电流；Iij.max为线路最大允许载流量。

(4)上级电网输入功率约束。

0≤pg.t≤pg.max

(7)

式中pg.max为配电网与上级电网交换功率的上限。

1.2 下层优化模型

下层优化模型在上层给定充放电合同电价的基础上确定BESS的最优容量与最优功率配置及各时刻充放电功率。目标函数如下：

maxFBESS=Bnop+Baop-Ctol

(8)

式中：FBESS代表BESS运营商的经济效益；Bnop为BESS在系统正常运行过程中通过低储高发获得的运行收益，表达式见式(9)；Baop为BESS在系统故障过程中参与紧急需求侧响应获得的故障收益，表达式见式(10)；Ctol为BESS的配置成本[9]。

(9)

(10)

下层模型满足以下约束条件：

(1)储能电池在任意时间段内充电、放电仅能存在其中一种状态，如式(11)：

(11)

为线性化约束条件，式(11)也可用式(12)表示。

(12)

式中：λm为0-1二值变量；M为一数值较大的正数。

(2)电池的荷电状态(state of charge，SOC)，与每时刻充放电功率有关，应满足如式(13)所示的递归关系。并且为保证下一调度周期内储能系统具有最大的灵活性，将初始时刻电池的荷电状态定为50%[10]。

(13)

式中：ηc、ηd分别为BESS的充放电效率；Soc.t为t时刻储能系统的荷电状态；ΔT为单位时间间隔，本文取1 h。

为减小电池寿命损耗，电池的荷电状态不能超出其物理允许的上下限：

Soc.min≤Soc.t≤Soc.max

(14)

式中Soc.max和Soc.min分别为储能系统物理允许的荷电状态上下限。

一般而言，电池允许充放电的最大功率与额定容量有关，满足式(15)。

(15)

式中γc、γd分别为单位时间内充、放电的最大功率与储能电池额定容量Snom的比值。

1.3 双层模型结构

双层模型结构示意图如图2所示。

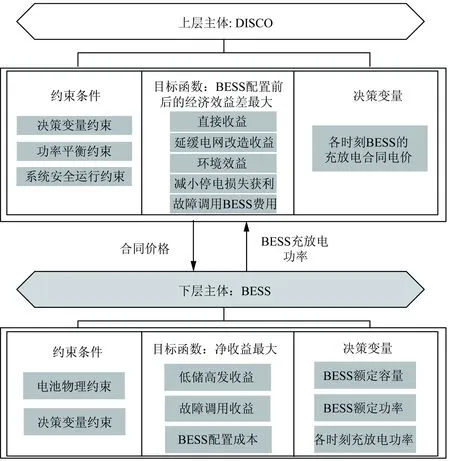
图2 BESS最优容量与合同价格双层优化模型Fig.2 Bi-level optimization planning method of BESSoptimal capacity and contract price

2 模型求解算法

上层模型为经济调度问题，由于常规粒子群算法没有考虑到迭代过程中的粒子特性，取值缺乏指导，故本文采用改进粒子群算法(improved particle swarm optimizer，IPSO)进行求解[11]。

针对PSO算法存在易陷入局部最优的缺点，本文引入Cauchy-Gaussian消减变异因子[12]，对局部最优极值进行扰动调整。对粒子个体位置xi=[xi.1,xi.2,…,xi.d]执行Cauchy-Gaussian消减变异后的位置如式(16)、(17)所示。

xi=[xi.1×Δ,xi.2×Δ,...,xi.d×Δ]

(16)

Δ=1+ξ[(α×k)/K]×δ

(17)

式中：ξ称为变异能效系数，服从式(18)；δ为消减变异因子，满足式(19)；K为最大迭代次数。

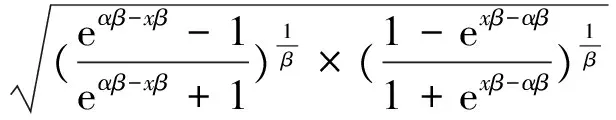
x∈[0,α],ξ∈[0,1)

(18)

式中α和β是控制参数。当x取最小值时，ξ取值接近于1；当x取最大值时，ξ取值为0；当x取值于最大值和最小值之间的某数值时，ξ为1和0之间的消减数值。当ξ越大时，变异效能越大。

(19)

式中：C(0,1)是标准柯西分布；G(0,1)是标准的高斯分布；Υ为分段控制变量，取值为黄金分割点0.618；k为当前迭代次数。由此可见，Cauchy-Gaussian动态消减变异因子δ融合了Cauchy变异和Gaussian变异，其中Cauchy变异的扰动能力强于Gaussian变异，适合于全局开发，而Gaussian变异更适合于局部搜索。根据迭代的进程交替选用Cauchy变异和Gaussian变异，从而可同时提高求解精度和速度。

下层模型为BESS优化配置问题，属于非凸非线性优化问题，可采用MATLAB中的YALMIP工具箱求解[13]。

模型求解过程如图3所示。

3 算例分析

3.1 系统参数

本文以改进IEEE-33节点系统为例进行研究，并引入分布式风电，位置及容量分布见图4，规划基准年峰值负荷为3.775+j2.300 MV·A，向上级电网购电的BESS以新兴的钠硫电池为例，电池相关参数[9]见表1，配电网向上级电网购电的实时电价如图5所示，该级电网售电电价取为购电电价的1.2倍[14]。上级电网生产单位电能的污染物排放情况[9]见表2。系统元件故障率和修复时间如表3所示。其余系统参数参见表4。

图3 双层模型求解流程图Fig.3 Bi-level model solving process

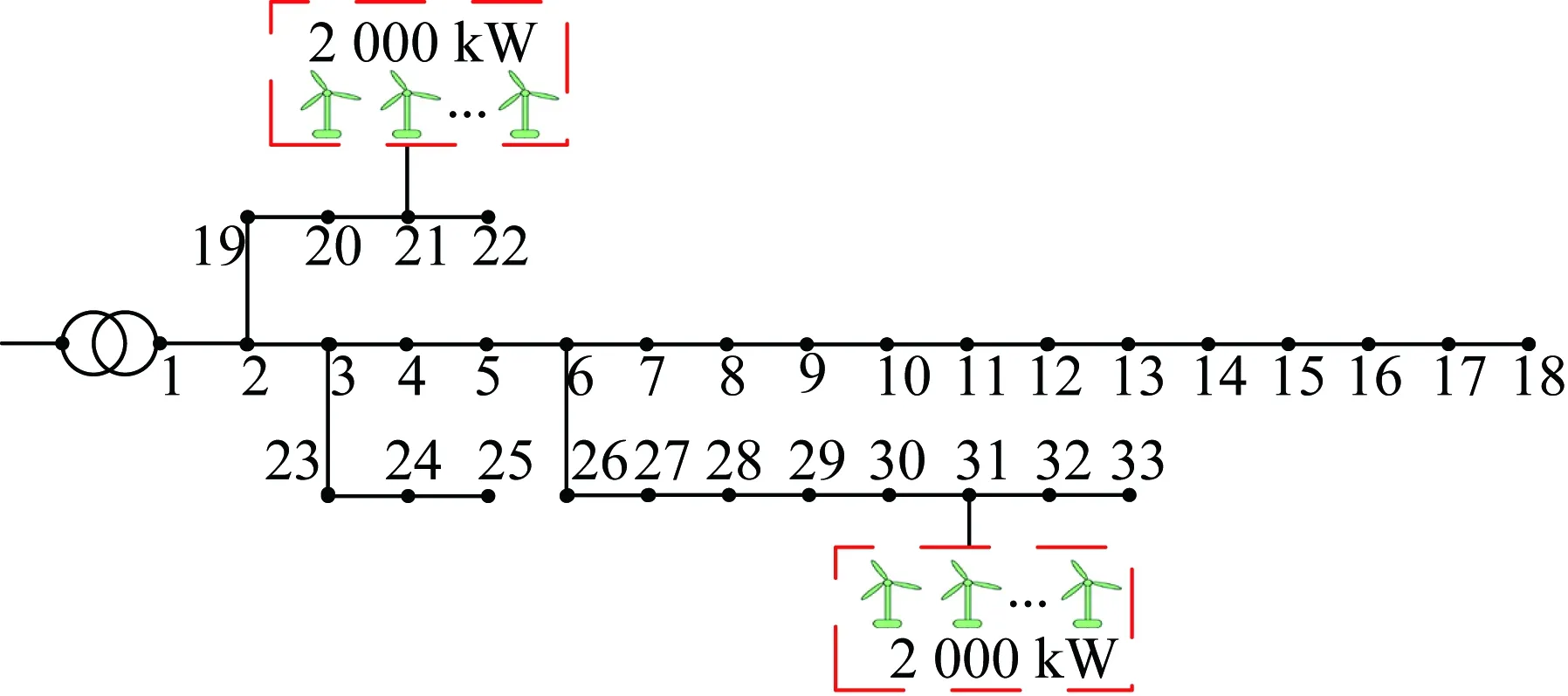
图4 改进IEEE-33节点系统Fig.4 Modified IEEE-33 nodes system

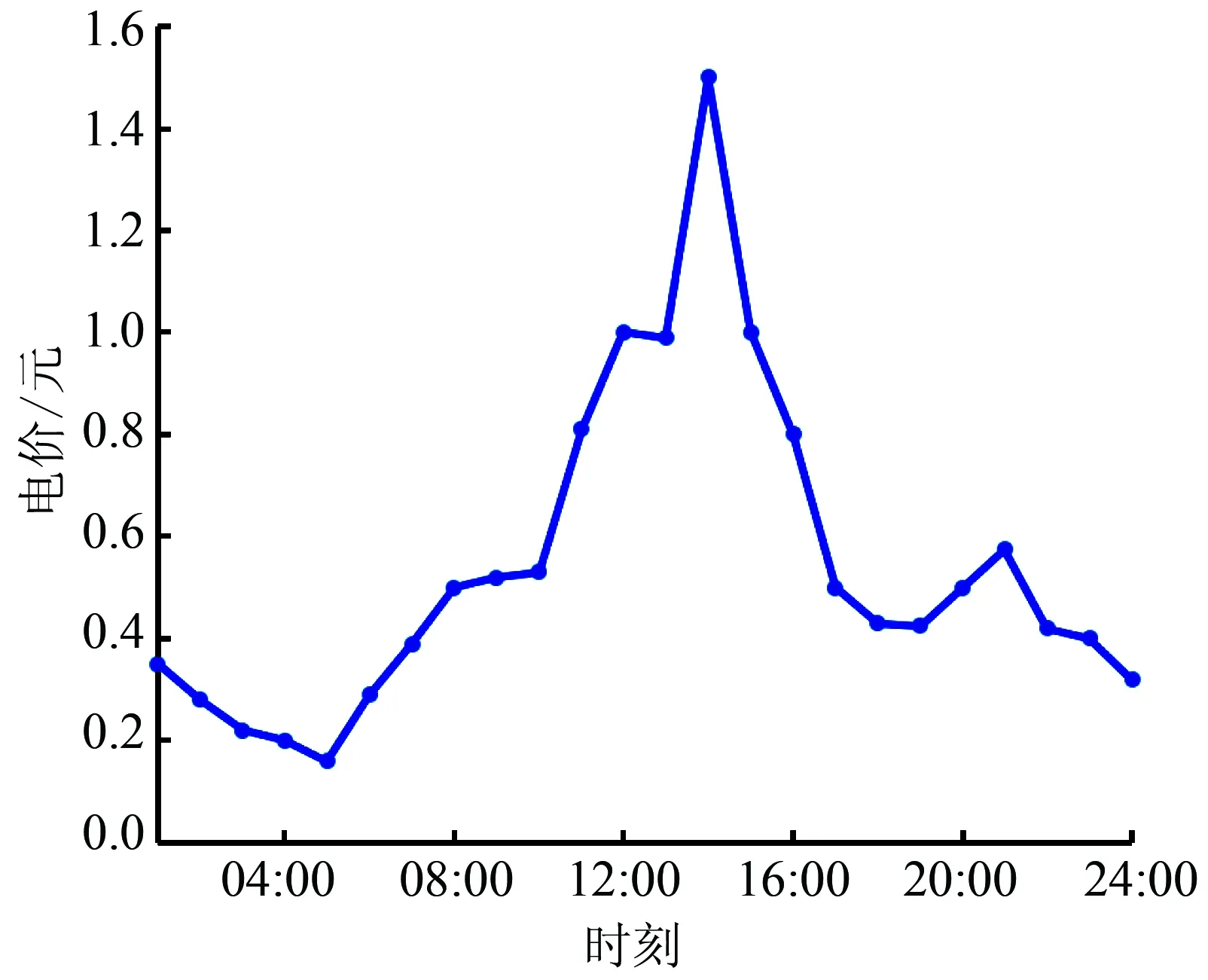
图5 配电网向上级电网购电的实时电价Fig.5 Spot price of distribution network purchasingfrom upper system

表3 元件故障率和修复时间Table 3 Failure rate and repair time of elements

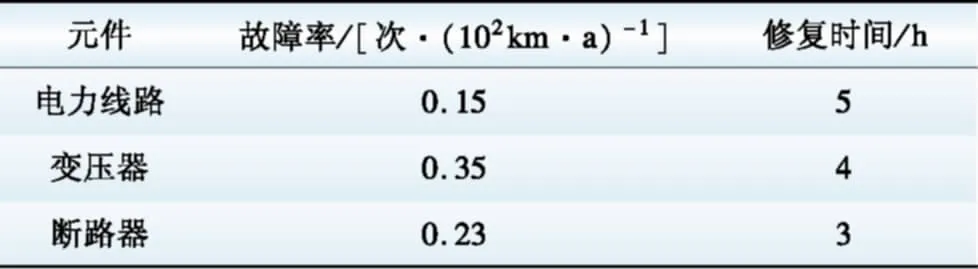
表4 系统参数Table 4 System parameters

3.2 优化结果

为验证所提方法的有效性，本文对比分析了2种方案的优化结果，其中方案一为原始方案，DISCO不参与BESS的优化配置过程，BESS运营商以自身利益最大(即仅计及下层目标maxFBESS)为配置目标；方案二为本文所建立的双层优化方法。优化结果如表5—7所示。

表52个方案中BESS最优配置结果及各项收益
Table5BESSoptimalallocationresultsandbenefitsoftwocases

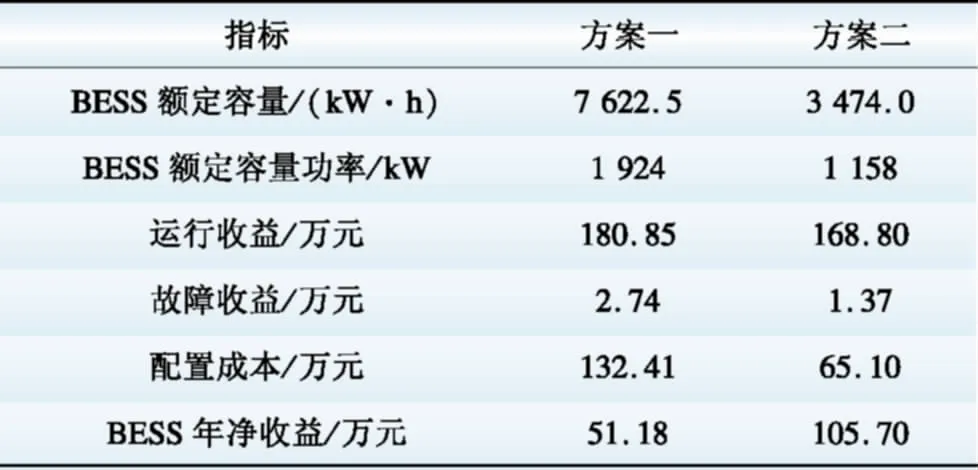
表6 2个方案中DISCO收益Table 6 DISCO benefits of two cases

万元

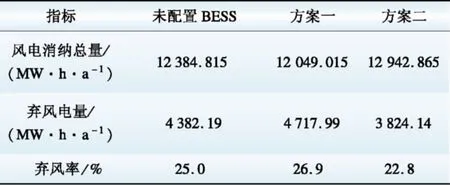
表7 不同方案下风电消纳情况Table 7 Wind power absorption in different schemes

2种方案中BESS各时刻充放电功率及合同电价如图6所示。

图6 2种方案下BESS各时刻充放电功率及合同电价Fig.6 BESS charge and discharge power ofeach time amp; contract price in two cases

表5显示，在方案1中，电池储能系统的配置规格为1 924 kW/7 622.5 kW·h，比在方案2中的配置规模要大。这是因为，方案1仅考虑BESS自身利益，即由低储高发获得的运行收益与故障过程获得的收益。而此时，BESS的低储高发的标准为原始电价，由图6可知，原始电价的波动性与合同电价相比要小很多。因此，BESS要想获得较高的收益，只能增大容量和功率。与此同时，成本也在增加，当收益的增加幅度小于成本的增加幅度时，净收益开始减小，存在一个净收益的最高点，此时即对应BESS容量和功率的最优值。

另一方面，方案一环境效益为负值且数值较大，是影响DISCO总增值收益的主要因素。导致方案一中环境效益为负的主要原因有2个，其一BESS本身存在功率损耗，充电总功率大于放电总功率；其二BESS充放电策略的制定仅考虑自身利益，即仅关注配电网的售电电价，这就导致与配电网的实际负荷需求不符，如在01:00时，风电大，但负荷需求较小，BESS应充电，但此时电价较高，BESS仅关注自身利益而选择放电，造成更大量的弃风；反之，在17：00时，风电不足以满足原始负荷需求，BESS应放电，弥补风力发电的不足，但由于此时电价较低，BESS选择在该时刻充电，DISCO必须向上级电网购入更多电能，最终导致环境效益恶化。为验证该结论，在表7中对比显示2种方案下风电的利用情况，其中方案一的弃风率相比于未配置BESS时更大。采用双层规划方法后(方案二)，DISCO通过制定合理的BESS充放电合同电价，对BESS的充放电过程进行了修正，从而使得DISCO的环境效益显著提高，并且风电利用率也得到提升。

另外，由表6可知，方案二中除减小停电损失获利以外的其他收益均比方案一中有所提高，且由图7可知，除23：00外，BESS各时刻充放电合同电价均比原始电价高，且波动幅度增大，这说明双层规划方法中DISCO通过设定合同电价实现对BESS的优化调度，进而深入挖掘BESS在配电网层面配置的多种潜在收益，使得自身利益最大。同时，合同电价实现了DISCO与BESS之间的收益转移，使得BESS也从中获利，验证了本文所提方法的有效性。而减小停电损失获利与BESS的额定配置容量与功率呈正相关，由表5可知，方案二中BESS最优额定容量、额定功率均比方案一小，因此，方案二中减小停电损失获利较小，另一方面也表明DISCO参与BESS的优化配置过程，可减小BESS的容量及功率需求，防止BESS配置的无序增长。

3.3 不同DG类型的影响

不同类型的DG具有不同的出力特性，对BESS容量配置及充放电合同电价的制定影响较大。为考虑不同DG类型对本文模型优化结果的影响，将算例中风电替代为等容量的光伏，其出力特性及优化结果分别如图7和表8所示。

图7 风电、光伏出力及原始负荷曲线Fig.7 WTG, PV output and original load curve

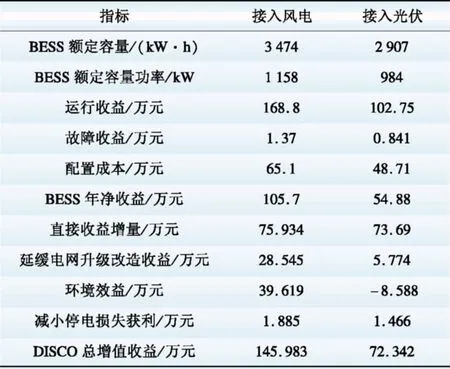
图8 不同DG接入BESS各时刻充放电功率及合同电价Fig.8 Optimization results of different DGs

由图7可知，光伏具有正负荷调节特性，由于各时刻系统原始负荷均大于光伏出力，因此该种情形下配置BESS不能减小DISCO向上级的购电电量，相反，由于BESS本身存在能量损耗，配置BESS后将增大DISCO从上级的购入电量，导致环境效益的恶化。表8中接入光伏时DISCO的环境效益为负值可证明这一结论。DISCO收益的降低直接影响到对BESS的调度过程，由图8可知，光伏接入情况下BESS充放电的平均合同电价也降低，进一步影响BESS的优化配置，因此，表8中光伏接入情况下BESS的额定容量、额定功率和净收益均比接入风电时降低。可以预计，如果环境效益的减少量比其他3项收益之和更大时，将不能寻找到使BESS和DISCO同时受益的合同电价。由此可知，接入DG的类型将影响到采用本文方法计算所得的DISCO与BESS收益，当系统中接入具有逆调峰特性的风电比接入具有正调峰特性的光伏更能凸显储能的效益。

4 结 论

(1)双层规划方法使得DISCO通过合同电价实现对BESS的优化调度，从而间接参与到BESS的优化配置过程中；合同电价实现了DISCO与BESS之间的收益转移，使得BESS也从中获利。

(2)采用本文方法计算所得的DISCO与BESS收益受接入DG类型的影响较大，系统中接入具有逆调峰特性的风电比接入具有正调峰特性的光伏更能凸显储能的效益。

在当前储能补贴力度不足的现状下，本文的研究工作提供了一种新的储能配置方法，对促进储能系统的发展具有一定的实际意义和参考价值。

[1] 北极星储能网. 中国储能需求细分我国近年来储能政策大盘点[EB/OL]. (2016-04-05)[2017-03-10]. http://news.bjx.com.cn/html/20160405/722076.shtml.

[2] 颜志敏, 王承民, 郑健, 等. 配电网中蓄电池储能系统的价值评估模型[J]. 电力自动化设备, 2013, 33(2): 57-61.

YAN Zhimin, WANG Chengmin, ZHENG Jian, et al. Value assessment model of battery energy storage system in distribution network [J]. Electric Power Automation Equipment, 2013, 33(2): 57-61.

[3] 向育鹏, 卫志农, 孙国强, 等. 基于全寿命周期成本的配电网蓄电池储能系统的优化配置[J]. 电网技术, 2015, 39(1): 264-270.

XIANG Yupeng, WEI Zhinong, SUN Guoqiang, et al. Lifecycle cost based optimal configuration of battery energy storage system in distribution network [J]. Power System Technology, 2015, 39(1): 264-270.

[4] 温俊强, 曾博, 张建华. 市场环境下考虑各利益主体博弈的分布式电源双层规划方法[J]. 电力系统自动化, 2015, 39(15): 61-67.

WEN Junqiang, ZENG Bo, ZHANG Jianhua. Bi-level programming method for distribution generator considering stakeholders game relationship in an electricity market environment [J]. Automation of Electric Power Systems, 2015, 39(15): 61-67.

[5] 曾博,刘念,张玉莹,等. 促进间歇性分布式电源高效利用的主动配电网双层场景规划方法[J]. 电工技术学报,2013,28(9):155-163.

ZENG Bo, LIU Nian, ZHANG Yuying, et al. Bi-level scenario programming of active distribution network for promoting intermittent distributed generation utilization [J]. Transactions of China Electrotechnical Society, 2013, 28(9):155-163.

[6] NGUYEN H T, CUONG T D, SHAOLEI R, et al. Incentive mechanisms for economic and emergency demand responses of colocation datacenters[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(12): 2892-2905.

[7] LIU W X, NIU S Y, XU H T. Optimal planning of battery energy storage considering reliability benefit and operation strategy in active distribution system[J]. Journal of Modern Power System Clean Energy, 2017, 5(2): 177-186.

[8] LIU W X, XU H T, NIU S Y, et al. Optimal distributed generator allocation method considering voltage control cost[J]. Sustainability, 2016,8(2):193.

[9] 刘文霞, 牛淑娅, 石道桂, 等. 考虑运行策略及投资主体利益的主动配电系统储能优化配置[J]. 电网技术, 2015, 39(10): 2697-2704.

LIU Wenxia, NIU Shuya, SHI Daogui,et al. Optimal allocation of ADS battery energy storage considering operation strategy and investment subject benefit[J]. Power System Technology, 2015, 39(10): 2697-2704.

[10] 蒋程,刘文霞,张建华. 含电池储能风电场的电力系统风险评估[J]. 电网技术,2014,38(8):2087-2094.

JIANG Cheng, LIU Wenxia, ZHANG Jianhua. Risk assessment for power system with wind farm and battery energy storage[J]. Power System Technology, 2014, 38(8):2087-2094.

[11] 吴小刚, 刘宗歧, 田立亭, 等. 基于改进多目标粒子群算法的配电网储能选址定容[J]. 电网技术, 2014, 38(12): 3405-3411．

WU Xiaogang, LIU Zongqi, TIAN Liting, et al. Energy storage device locating and sizing for distribution network based on improved multi-objective particle swarm optimizer [J]. Power System Technology, 2014，38(12)：3405-3411.

[12] 杜晓昕,张剑飞,郭媛,等. 基于柯西-高斯动态消减变异的果蝇优化算法研究[J]. 计算机工程与科学,2016,38(6):1171-1176.

DU Xiaoxin, ZHANG Jianfei, GUO Yuan,et al. A fruit fly optimization algorithm with Cauchy-Gaussian dynamic reduction mutation[J]. Computer Engineering amp; Science, 2016, 38(6): 1171-1176.

[13] LOFBERG J. YALMIP: A toolbox for modeling and optimization in MATLAB[C]//In Proceedings of the 2004 IEEE International Symposium on Computer Aided Control. Systems Design. Taipei, Taiwan:IEEE, 2004:284-289.

[14] 牛淑娅,曾博,刘文霞,等. 基于合作博弈的电动汽车换电站优化配置[J]. 南方电网技术,2016,10(12):53-60.

NIU Shuya, ZENG Bo, LIU Wenxia, et al. Cooperative game based optimal capacity configuration model of battery switch station for electric vehicles [J]. Southern Power System Technology, 2016, 10(12):53-60.

[15] 张世翔,邵慧壮. 基于分布式电源的配电网综合效益评估[J]．上海电力学院学报, 2015, 31(1): 19-23．

ZHANG Shixiang, SHAO Huizhuang. Overall efficiency assessment of power distribution network based on distribution network[J]. Journal of Shanghai University of Electric Power, 2015，31(1): 19-23.

2017-05-20

刘译聪(1994)，女，通信作者，硕士研究生，主要研究方向为电力系统规划、储能技术；

牛淑娅(1991)，女，硕士，主要研究方向为配电网规划与电池储能技术；

杨洋(1992)，女，硕士研究生，主要研究方向为电力系统规划；

刘文霞(1967)，女，博士，教授，主要研究方向为电力系统规划与可靠性、电力系统风险评估、电力系统通信；

李永贤(1964)，男，本科，高级工程师，主要从事电力安全管理工作；

刘座铭(1982)，男，硕士，教授，高级工程师，主要研究方向为电力系统稳定计算及电能质量。

(编辑 张小飞)

Bi-LevelOptimizationPlanningMethodofBatteryEnergyStorageSystemOptimalCapacityandContractPrice

LIU Yicong1, NIU Shuya2, YANG Yang1, LIU Wenxia1, LI Yongxian3, LIU Zuoming4

(1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China; 2. Chengxi Power Supply Branch Company, State Grid Tianjin Electric Power Company, Tianjin 300110, China; 3. State Grid Ningxia Electric Power Company, Yinchuan 750001, China; 4. Jilin Electric Power Research Institute, Changchun 130012, China)

Battery energy storage system (BESS) with abilities of both power supply and storage has become important control measure of power grid optimizing operation. With the application scenarios that battery independent operators invest BESS at the distribution network level, and distribution company (DISCO) guides the charging and discharging strategy of BESS in the form of contract price, this paper proposes a bi-level optimization planning method of BESS optimal capacity and contract price. In view of the model solving process easy to fall into local optimum, this paper improves adaptive weighted formula of particle swarm algorithm, introduces the Cauchy-Gaussian reduction mutation factor, as well as disturbs and adjusts the local optimum extremum. IEEE-33 nodes distribution system is taken as an example to verify the validity and feasibility of the model.

battery energy storage system; contract price; optimal capacity allocation; improved particle swarm algorithm; bi-level optimization planning

国家电网公司科技项目(B3441317K002)

TM715

A

1000-7229(2017)11-0097-08

10.3969/j.issn.1000-7229.2017.11.013