基于排序算法的MMC电容电压均衡策略对比研究

王坤，刘开培，王思茹，李威，王玉，冉晓洪

(1. 武汉大学电气工程学院，武汉市430072；2.南瑞集团公司(国网电力科学研究院)，南京市210003)

基于排序算法的MMC电容电压均衡策略对比研究

王坤1，刘开培1，王思茹1，李威2，王玉2，冉晓洪1

(1. 武汉大学电气工程学院，武汉市430072；2.南瑞集团公司(国网电力科学研究院)，南京市210003)

基于排序算法的模块化多电平换流器(modular multilevel converter, MMC)电容电压均衡策略能够快速平衡模块电压，广泛应用于实际工程，但是实时排序会占据控制器大量计算资源，并且开关器件的高频动作将引起较大的开关损耗。为此，在保持模块电压均衡的同时，有必要着重关注均衡策略的时间复杂度和开关频率。在传统的排序算法均衡策略的研究基础之上，按照不同的优化目标将现有的改进策略分为3类，从不同评价指标对3类改进策略进行比较和分析。最后，探讨MMC均压策略的未来研究方向和发展趋势，为解决MMC模块电压不平衡问题提供借鉴。

模块化多电平换流器(MMC)；电压均衡策略；排序算法；时间复杂度；开关频率

0 引 言

模块化多电平换流器(modular multilevel converter, MMC)具有输出波形好、开关频率低、扩展性强等优势，在高压大功率领域得到广泛应用[1-2]。随着电压等级的提高，MMC所需要的子模块(sub-module, SM)数量越来越多[3]，例如舟山采用模块化多电平换流器的高压直流输电系统(MMC based high voltage direct current, MMC-HVDC)中单个桥臂子模块数达到250个，而在建的大连双端MMC-HVDC工程直流电压等级为±320 kV，桥臂子模块设计数量为400个[4-5]。然而大量串联的子模块不仅增加了MMC系统复杂性，同时也为MMC悬浮电容电压均衡控制带来了新的挑战[6-7]。

目前，国内外对MMC的电容电压均衡策略展开了大量的研究并取得了丰硕的成果，均压策略大致分为2类。一类是为每个子模块配置1个闭环的均衡控制器，补偿电流内环输出电压调制波，但是这种均衡策略将会引入大量的附加控制器，极大地增加了控制系统的复杂性[8-9]。另外一类是基于排序算法的电压均衡策略，根据电流方向选择合适的模块投入，是一种对模块电压的整体控制[10-11]。排序算法均衡策略原理简单，易于实现，均压效果优异，已投运的MMC实际工程验证了其有效性[12]。但是随着模块数量的增加，传统排序算法时间复杂度高，将占据大量的计算资源[13]。当MMC应用于高频领域时，庞大的计算量将在控制环节中引入较大的延迟，已难以满足控制系统实时性的要求，影响系统响应特性和稳定性[14]。同时，开关器件的频繁动作，也会造成总的开关损耗急剧增加，影响器件的使用寿命[15]。因此，现有的文献对传统的基于排序算法的均衡策略进行了多种优化和改进。关于排序算法的改进策略可以分为3类，前2类改进策略侧重于降低算法的时间复杂度，减少均衡策略的计算量。不同的是，第1类改进策略能够保证模块的选择机制不变，均压效果优异；而第2类改进策略会改变模块的投切状况，均压效果有所下降。第3类改进策略重点研究开关器件的降频手段，能有效减少开关损耗，但是存在模块电压均衡效果减弱的问题。

本文主要研究基于排序算法的电容电压均衡及其改进策略，将现有的电压控制策略进行整理分类，阐述每一类改进策略的作用机理并从计算量、均压效果和开关频率3个方面进行比较分析。最后，本文对排序算法均衡策略的未来研究方向进行展望，以期对该领域的进一步发展和完善提供参考。

1 MMC工作原理

典型的半桥MMC拓扑如图1所示，三相共有6个桥臂，每个桥臂由N个完全相同的子模块和桥臂电感L串联组成，子模块采用半桥子模块 (half-bridge sub-module, HBSM)。子模块中的悬浮电容C储存系统能量，其中并联的快速旁路开关K1和晶闸管T1可以避免故障时系统断电，同时能够限制流过开关管的冲击电流，提高系统和器件运行的可靠性。

MMC调制策略通过控制开关管触发信号输出期望的交流电压并实现相关附加功能[16-17]，如环流抑制、电容电压均衡等。目前，较为成熟的调制方式包括载波移相正弦脉宽调制(carrier phase shifted-sinusoidal pulse width modulation, CPS-SPWM)和最近电平逼近调制(nearest level modulation, NLM)。NLM控制上、下桥臂投入的模块个数，利用阶梯波不断逼近调制波形，实现简单，在实际工程中得到广泛应用。每相上桥臂和下桥臂实时投入的模块数满足：

图1 MMC拓扑

(1)

式中：ni1、ni2分别为第i(i=a, b, c)相上桥臂和下桥臂应当投入的子模块数;uim为第i相调制电压；Round(·)为最近取整函数(四舍五入取整)。

可以看出，虽然上、下桥臂投入运行的模块数随着调制波实时变化，但是每相投入的模块总数始终一致为N，这种调制特性可以维持直流电压Ud恒定，保障系统稳定运行。

相比于两电平电压源换流器(voltage source converter, VSC)，MMC悬浮电容的设计能够减少直流侧故障时的电容冲击电流，但同时也带来一定的问题。由式(1)可知，受调制策略影响，桥臂中处于投入与切除状态的子模块数量实时变化，导致各模块充、放电时刻和持续时间存在差异，同时由于器件参数不尽相同，势必会造成模块电容电压的不均衡，危及换流器的正常运行。

2 基于排序算法的电容电压均衡策略

模块电容电压均衡策略一般依据采取的调制手段而定，对于高频的PWM调制，通过设置均衡控制器和平均控制器实现电压平衡，这种方法的缺点是随着子模块的数量增加，所需要的附加控制器越来越多，大大增加控制系统的复杂性和参数的整定难度[8-9]。对于NLM调制，实际应用中通常采取基于排序算法的电容电压均衡策略。根据电容电压排序结果和系统能量变化，选择合适的触发模块实现电容电压均衡，其过程如图2所示。首先实时采集桥臂各模块电容电压值，根据排序算法得到模块电压的有序排列。判断子模块电容充、放电情况，并根据NLM调制输出桥臂实时投入的模块个数n，当电流i方向对子模块充电时投入电压最低的n个子模块；反之，则投入电压最高的n个子模块。该策略能够对低电压模块充电，并对高电压模块放电，迅速抑制电容电压间的不均衡，效果优异。

文献[18-19]将CPS-SPWM中调制波和各个载波的比较结果相加作为桥臂模块的投入数量，引入电压排序的均衡算法，可以大大简化基于高频PWM调制的MMC均压控制系统。可以看出，基于排序算法的电容电压均衡策略不仅均衡效果优异，而且具有较强的可移植性和适用性，因此在实际工程中得到广泛应用。电压排序均衡策略的核心环节是对模块电压数据进行处理，快速、准确地将无序数据组转变成有序排列，为下一步的判断和选择触发提供基础。排序算法占据了均衡策略的主要计算量，随着模块数的增多，必将占用大量的计算资源，影响系统运行速度甚至系统的动态跟踪特性[13-14]。因此，通过分析不同排序算法的排序过程和时间复杂度，研究不同排序模式对均衡策略及系统响应的影响，考虑具体应用中对开关频率的要求，选择合理高效的电压均衡策略在MMC实际工程中具有重要意义。针对上述问题，已有大量文献从不同角度提出了相关改进措施。

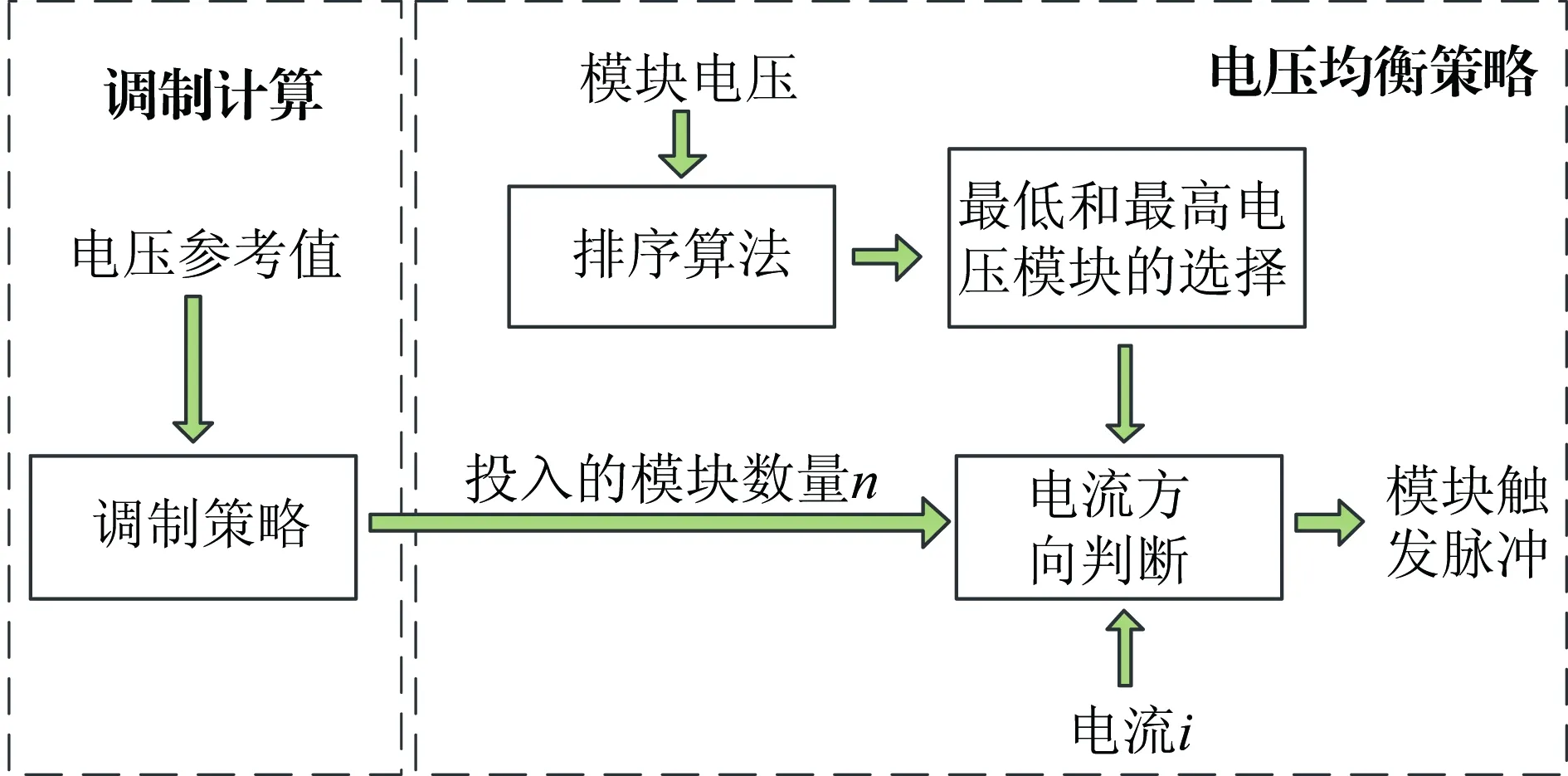
图2 基于排序算法的电容电压均衡策略Fig.2 Capacitor voltage balancing strategybased on sorting algorithm

3 基于排序算法的改进均衡策略

3.1 降低计算量的A型改进策略

传统的基于排序算法的均衡策略能够快速地平衡模块电压，是目前实际应用中均压效果最好的均衡策略[20]。传统均衡策略的主要问题之一在于排序算法和模块选择过程计算量较大，对控制器的计算性能提出了较高的要求甚至危及系统的稳定运行[21]。降低计算量的A型改进策略从排序算法的选取优化和排序模式的改进2方面切入，能够行之有效地降低算法计算量并能够保持均衡效果不变。

3.1.1排序算法选取及优化

排序算法的目标是将采集的模块电压有序化，选择对应的模块投入或者切除以实现电压均衡。不同的排序算法时间复杂度不同，所需的排序计算量相差甚远，选取不同的排序算法或者对排序算法进行优化可以有效缓解模块数量增加带来的计算负担。冒泡排序(bubble sort)是一种简单实用的排序方法，算法经典可靠，在MMC均压算法中应用颇广[22]。然而，冒泡排序的时间复杂度为O(n2)，随着模块数量的增加，排序运算量呈平方增加，严重加大控制器的负担。快速排序(quick sort)算法由TONY H在1962年首次提出[23]，基于比较、划分思想，采用分治技术，整个排序过程可以递归进行，时间复杂度为O(nlog2n)，是实际应用中最快的一种排序算法[24]。8个子模块电压数据组U=[4,6,3,1,8,7,2,5]的快速排序算法的排序过程如图3所示。

图3 快速排序过程Fig.3 Quick sort process

快速排序算法的核心在于划分数据组元素的选取，文献[25]提出一种基于改进快速排序算法的均衡策略，取数据组的平均值作为划分元素，确保每次划分后两个子数据组具有相似的数据长度，相比于传统快速排序算法可以大大减少比较次数，运算效率提高近17%。文献[26]从降低时间复杂度的角度对快速排序算法进行了优化，仅仅关注投入和切除模块的编号信息，避免了对投入组电压和切除组电压的排序，算法时间复杂度降为O(n)。同时，利用上一控制周期的排序结果选择枢纽元素，能够有效降低控制器的运算量。

文献[27]提出一种最高位优先(most significant digit first，MSD)的排序方式，从最高位开始对序列进行分组，逐渐消除逆序，将时间复杂度降为O(n)。理想情况下，所有模块电容完全相同，投入组和切除组的两组模块电压顺序在下一周期保持不变。非理想情况下，由于模块电容参数不尽相同，2组的模块电压顺序会随着电容的充放电发生改变。针对这一特点，文献[28-29]提出一种二路优化归并排序算法，避免了每个控制周期的全排序操作。考虑到非理想情况，采用直接插入排序对投入组和切除组电压分别

进行修正，可等效为理想情况，时间复杂度基本不变。

由于现场可编程门阵列(field-programmable gate array, FPGA)高度并行的结构及其固有的支持定制硬件设计的能力，在实际工程中，MMC的控制器架构大多由数字信号处理器(digital signal processing, DSP)+FPGA构成，DSP负责系统级的控制，而FPGA主要负责阀级控制的实现，包括电压排序、脉冲触发等。因此，借助FPGA的结构特点，文献[30-37]提出了不同的优化排序算法。为减少传统排序算法的计算量，文献[30]通过逻辑门和寄存器的配合使用提出一种“龟兔竞赛”的排序方法，通过获取电压最高或者最低的模块实现快速的电压均衡。但是这种方式在获取电压具体数值前已经完成排序，无法适用于相关的降频手段如对电压值进行保持因子校正，限制了其应用范围。文献[31]采用适用于FPGA的动态分组排序算法，将模块电压数据、电流方向等以二进制比特位的形式表示，从高位到低位依次比较各个数据的比特位，有效提高了排序效率。

然而，动态分组排序算法基于串行实现，并没有有效利用FPGA并行运算的硬件特点。奇偶排序[32]是冒泡排序算法的并行形式，能够充分利用FPGA的并行特点实现排序，文献[33]验证了其应用在电压均衡策略方面的正确性和有效性。排序网络算法[34]是基于比较网络模型，可以同时执行多个比较操作，适用于FPGA的并行结构。文献[35]利用排序网络执行模块电压的排序操作，分析了基于排序网络的奇偶排序和双调排序在均衡策略应用中的优势。文献[36]提出一种并行全比较的排序算法，对模块电压两两之间进行并行比较，比较结果进行累加，获得模块电压的有序序列。FPGA仅需要4个时钟周期即可完成并行全比较排序算法，时间复杂度固定。

不同排序算法在理论上不会改变有序电压序列的正确性，模块的触发机制不变，电容电压的均衡效果和系统特性理论上不发生改变，排序算法可替代性较好。

3.1.2排序模式的改进

排序算法的选取及优化本质上是对传统排序本身的研究，结合排序算法在MMC均衡策略中的应用特点，文献[37-39]对排序模式进行了相应的改进。

对于电压均衡策略而言，必须获取的信息是哪些模块需要投入，对需要投入的模块的排序情况并不关注，基于这种思想，文献[37]和[38]提出一种无需排序的均衡策略，原理如图4所示。假定桥臂模块个数为N，需要投入的模块数为k。当电流i≥ 0时，通过执行算法找到第k小电压值并和所有模块电压进行比较，即可得到电压最低的k个子模块(投入)和电压最高的N-k个子模块(切除)；当电流ilt;0时，则找到第k大值，并作类似的处理。这种策略得到的投入和切除子模块均处于无序状态，在保持电压均衡效果不变的情况下避免了对模块电压的全排序，时间复杂度大大降低。

图4 不关注排序情况的均衡策略Fig.4 Balancing strategy of not focusing on sorting

执行算法在文献[37]中是快速选择算法，也可以在FPGA中利用比特位比较实现[38]。类似地，文献[39]同样不考虑具体的电压数值及排序情况，提出一种映射均压控制策略。依据电压大小将模块位置信息存入存储阵列，按照特定的方向从存储器中依次读取投入和切除的模块位置信息，牺牲部分内存以提高均衡策略的执行速度。

可以看出，对排序模式的改进，能够形成多种基于广义排序算法的优化均衡策略。这些策略并没有从排序算法本身出发，更多的是结合电压均衡的特点，改进和优化模块的选择机制，在减少算法计算量的同时保证均衡效果不变。

3.2 降低计算量的B型改进策略

在现有涉及降低算法计算量的改进策略中，除了上述的A型改进策略，文献[40-51]提出了一类新型改进策略。此类改进策略侧重点在于对算法计算量的优化，均压效果随之下降，称为B型改进策略。文献[40]提出电压分层均衡思想，将模块电压分成M个容器，每层高度ΔU为

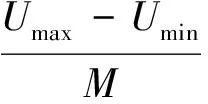
(2)

式中Umax、Umin分别是模块电压的最大值和最小值。

在每个控制周期内将每个模块根据每组电压的上、下限放入对应的容器，根据需要投入的模块数量和电流方向选择对应的容器投入或者切除。这种方法避免了排序运算，但是当投入的模块数量并非恰好等于若干个容器中模块数量之和时，部分模块的不精确投切将会造成电压均衡效果下降。

分层均衡控制中每个容器的模块动态变化，而文献[41-43]提出的模块电压分组排序算法中每组模块固定。分组排序算法对每组的模块电压分别排序，根据组间平衡算法分配各组投入的模块个数[41]。文献[42]根据质因子分解法确定模块分组形式，按照质因子由大到小的顺序对每层分组，可以证明这种方式所需要的排序次数最少。文献[43]提出将质因子分解法中的排序算法由冒泡排序改为混合排序：当分组数小于或等于2组或组内模块个数小于或等于2个时，组间或组内电压排序选用冒泡排序算法；当分组数大于2组或组内模块个数大于2个时，则选用希尔排序算法，进一步降低均衡策略所需要的排序次数。

类似于分组排序的优化思想，文献[44-45]提出了一种分布式电压均衡策略，对功率模块进行分组，通过设置桥臂电压的平均值和分组电压的平均值之间的闭环控制，修正各组的模块导通数量，因此即使发生故障，仍能维持健全模块的安全稳定运行。但是该策略需要为每组模块配置1个修正数量控制器，增加了系统的控制复杂性。

MMC控制器控制频率越高，电压均衡策略效果越好，电压波动会越小[46]。为了充分利用桥臂中各个子模块，降低系统谐波含量，控制频率需要足够高[47]。此时，每个控制周期内电平和模块数量变化较小，仅需要对电压最高或者最低的模块进行投切操作，因此只要获取模块电压的极值即可满足电压均衡的需求。文献[48-49]均是基于寻找最值的均衡思想，利用冒泡比较的原理确定投入组和切除组的最大模块电压和最小模块电压，在频率足够高的情况下能够保证均压效果较好。文献[50]表明，对基于全桥模块的MMC，寻找最值的均衡策略依旧有效，显著降低了控制器的计算量。文献[51]提出一种预测控制的均衡策略，预先计算模块在充电或放电阶段结束时所储存的能量，按照平均分配储能的原则选择模块触发，能够减小电压波动幅度，但是模块故障时均衡策略将会失去控制。

降低计算量的B型改进策略通过对排序方式和模块选择过程的改进，实现有效减少算法计算量的优化目标，但是牺牲了部分均衡性能，导致模块电压的均压效果下降。

3.3 降低开关频率的改进策略

对排序算法或排序模式的研究，着眼点和落脚点均是减少算法计算量和维持均衡效果，鲜有涉及考虑降低器件的开关频率。评价电压均衡策略的指标有3类[52]，除了表征均衡效果的电压总体波动和电压的不平衡度外，器件的开关频率也是影响算法优劣的重要因素[53]。传统两电平和三电平换流器开关频率一般在1～2 kHz[54]，在不考虑降频的排序算法均衡策略的控制下，MMC每个控制周期均需要重新投切相应的模块，单个器件的开关频率一般在数百Hz[55]，总的开关损耗仍然较大，相比于传统换流器优势并不明显。

器件的开关频率越高，模块电压的均衡效果越好；开关频率降低，电压的波动和不平衡度将会增加[56]。因此，降频策略的核心在于掌控频率和均衡效果之间的取舍关系。文献[57-59]在传统均压策略中引入模块电压最大偏差的概念，提出一种仅投切新增子模块的优化均衡策略。当电压最大偏差高于预先设定值时，表明电压不平衡度较大，需要采取传统的均衡策略迅速平衡模块电压；当电压偏差较小时，表明电压不平衡度在允许范围之内，通过采取优化策略牺牲部分均衡性能降低开关频率。引入最大电压偏差的优化均衡策略如图5所示，k为当前周期需要投入的模块个数，kold为上一周期投入的模块个数，Δk是投入模块的变化量。当k=N时，所有的模块投入；但k=0时，所有的模块切除；当0lt;klt;N时，需要判断Δk的状态。当需要投入的模块增加时，在已切除的模块中按传统策略投入|Δk|个模块；当需要投入的模块减小时，在已投入的模块中按传统策略切除|Δk|个模块；当需要投入的模块数量不变时，则模块触发情况保持不变。这种处理可以在电压偏差允许范围内尽可能地避免器件的反复投切，减少不必要的开关工作，降低开关频率[58]。

随着最大电压偏差允许值的增加，开关频率随之下降，电压均衡效果将会变差[57]。设置电压偏差的降频思想，凭借其简单有效的特点，被国内外学者广泛引用[59-61]。文献[59]在文献[57]的基础上，对投入和切除的子模块进行一定数量的轮换，在略微增加开关频率的情况下获得更好的均压效果。通过设置电压偏差允许值，对处于投入和切除状态的子模块进行对调，有效降低开关频率[60]。文献[61]提出一种基于平均值比较的均衡策略，无需排序操作，设置排序允许电压偏差减少小幅电压波动引起的开关动作次数。

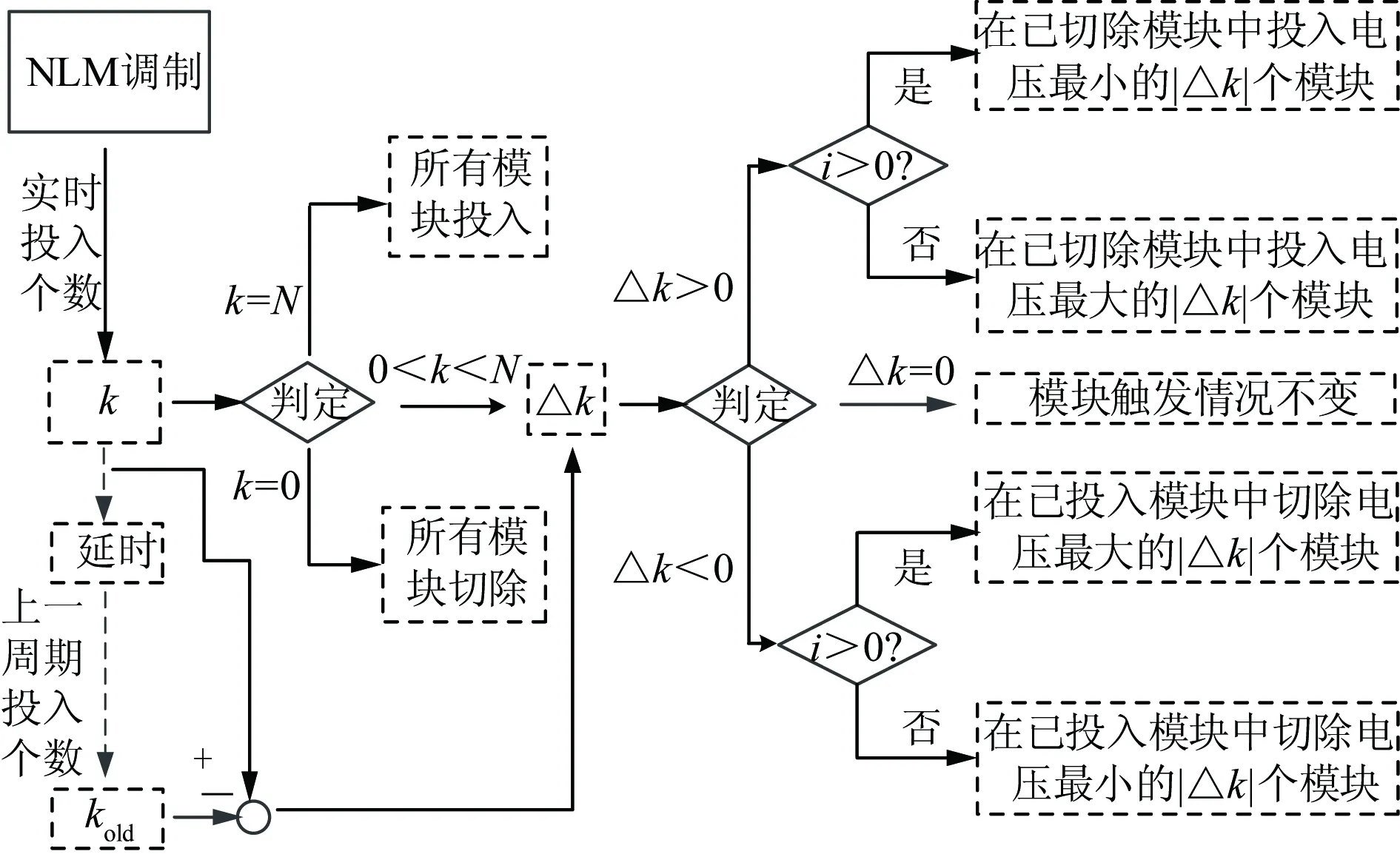
图5 引入最大电压偏差的优化均衡策略Fig.5 Optimized balancing strategy withmaximum voltage deviation

文献[62]提出一种直接的降频策略，传统的均衡策略中需要投切的模块一旦确定，投切动作立刻执行，即模块的选择频率和投切频率一致。文献[62]中设置的模块投切频率小于模块选择频率，可以直接有效地减少开关次数，但无疑增加了模块电压的波动幅度和不平衡度。文献[63]在模块电压额定值附近设置1组电压上、下限，优先动作电压越限的模块，对处于电压限值内的模块乘以1个略大于1的保持因子，赋予这些模块一定保持投切状态的能力，尽可能地避免处于电压限值内的模块频繁动作。当保持因子等于1时，等同于传统的均压控制策略。当选取的保持因子大到一定程度，器件的平均开关频率能够降到72 Hz[63]，但是这种处理同样也会造成模块电压的一致性变差。文献[64]在此基础上提出一种双保持因子的均衡策略，2个保持因子因此互为倒数，分别乘以处于投入和切除状态的模块电压，其目的是在下一控制周期中尽可能保持上一控制周期的模块投切状态以降低开关频率。在双保持因子的均衡策略中引入一种能够精确控制开关频率的比例积分(proportional integral, PI)控制器，以保证系统的高效稳定运行[65]。

这些改进的均衡策略均能够有效降低开关频率，但是鉴于开关频率和均衡效果之间的矛盾关系，此类策略往往会引发电压均衡效果变差的问题，因此需要根据实际应用需求对相应的调节参数进行合理的整定。

4 3类改进策略对比分析

根据前文分析，上述3类基于排序算法的改进策略的综合比较见表1。3.1、3.2和3.3节中的改进策略分别定义为第1～3类均衡策略。

表13类改进策略的比较
Table1Comparisonof3improvedstrategies

可以看出，第1、2类策略均以减少算法计算量为优化目标，第3类策略则侧重于降低器件的开关频率。第1类策略针对排序算法本身和排序模式进行改进，有效降低了算法的计算量。该类策略的模块触发机制不发生变化，均压效果优异，开关频率依然较高，相对于传统的均衡策略未进行优化和改进。而第2类策略虽然降低了算法计算量，但是优化过程中改变了模块的投切状况，造成均压效果下降，对开关频率的影响需要结合具体的改进方法进行分析。第3类策略由于赋予了模块一定保持投切状态的能力，减少了开关器件反复动作次数，能够显著降低开关频率，但是均压效果相应地随之下降，对算法的计算量未进行优化。在MMC应用中，可以根据实际需求选择适合的均衡策略。

5 总结与展望

随着柔性直流输电系统电压等级和功率等级的不断增加，MMC桥臂中包含的子模块规模将会十分庞大，对电容电压均衡策略提出了极高的要求。本文对现有关于排序算法的电容电压均衡及改进策略进行了详细的研究和分类，第1、2类改进策略主要用以降低算法计算量，均压效果较好，而第3类改进策略着重研究降低开关频率的作用机理，牺牲了部分的均衡性能。尽管国内外学者对基于排序算法的均衡策略展开了大量的研究，但是仍有一些研究工作值得深入开展。

(1)实际工程中已越来越多地使用FPGA实现电压均衡，结合FPGA的并行处理特点对电压排序算法和模块选择模式进行改进，研究适用于FPGA的均衡策略，并在具体的均压控制中充分利用硬件本身的优势。

(2)模块电压的均衡效果和开关频率的高低存在着“此消彼长”的矛盾关系，有必要研究一种包括电压波动幅度、不平衡度、计算量和开关频率的综合评价体系，根据不同的应用场景选择对应的电压均衡策略。

(3)目前基于排序算法的电压均衡及改进策略大多没有考虑其对系统环流的影响，今后的工作中需要进一步评估均压策略对环流的影响程度，制定与之匹配的解决方案。

[1] 张静, 孙维真, 费建平, 等. MMC-HVDC的稳态运行范围研究[J]. 电力建设, 2015 (3): 1-6.

ZHANG Jing, SUN Weizhen, FEI Jianping, et al. Steady-state operating range of MMC-HVDC[J]. Electric Power Construction, 2015 (3): 1-6.

[2] 杨晓峰, 郑琼林, 薛尧, 等. 模块化多电平换流器的拓扑和工业应用综述[J]. 电网技术, 2016, 40(1): 1-10．

YANG Xiaofeng, ZHENG Qionglin, XUE Rao, et al. Review on topology and industry applications of modular multilevel converter[J]. Power System Technology, 2016, 40(1): 1-10.

[3] SONG Q, LIU W, LI X, et al. A steady-state analysis method for a modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3702-3713.

[4] 吴方劼, 马玉龙, 梅念, 等. 舟山多端柔性直流输电工程主接线方案设计[J]. 电网技术, 2014, 38(10): 2651-2657.

WU Fangjie, MA Yulong, MEI Nian, et al. Design of main connection scheme for Zhoushan flexible multi-terminal HVDC transmission project[J]. Power System Technology, 2014, 38(10): 2651-2657.

[5] 郑超, 滕松, 宋新立, 等. 百万千瓦级柔性直流接入大连电网后的系统特性分析[J]. 电力系统自动化，2013, 37(15): 15-19, 26.

ZHENG Chao, TENG Song, SONG Xinli, et al. Analysis on system characteristics after incorporation of ±320 kV/1 000 MW VSC-HVDC into Dalian power grid[J]. Automation of Electric Power Systems, 2013, 37(15): 15-19, 26.

[6] SAAD H, GUILLAUD X, MAHSEREDJIAN J, et al. MMC capacitor voltage decoupling and balancing controls[J]. IEEE Transactions on Power Delivery, 2015, 30(2), 704-712.

[7] DENG F, CHEN Z. A control method for voltage balancing in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 66-76.

[8] HAGIWARA M, NISHIMURA K, AKAGI H. A medium-voltage motor drive with a modular multilevel PWM inverter[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1786-1799.

[9] 朱晋, 韦统振, 霍群海, 等. 基于动态偏置分配PD-PWM的变桥臂换流器子单元电容均压策略[J]. 电工技术学报, 2016, 31(15): 170-177.

ZHU Jin, WEI Tongzhen, HUO Qunhai, et al. A dynamic bias distribution PD-PWM strategy for alternate arm module multilevel converter[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 170-177.

[10] ROHNER S, BERNET S, HILLER M, et al. Modulation, losses, and semiconductor requirements of modular multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2633-2642.

[11] 丁冠军, 丁明, 汤广福, 等. 新型多电平VSC子模块电容参数与均压策略[J]. 中国电机工程学报, 2009, 29(30): 1-6.

DING Guanjun,DING Ming, TANG Guangfu, et al. Sub-module capacitance parameter and voltage balancing scheme of a new multilevel VSC modular[J]. Proceedings of the CSEE, 2009, 29(30): 1-6.

[12] 汤广福, 庞辉, 贺之渊. 先进交直流输电技术在中国的发展与应用[J]. 中国电机工程学报, 2016, 36(7): 1760-1771.

TANG Guangfu, PANG Hui, HE Zhiyuan. Ramp;D and application of advanced power transmission technology in China[J]. Proceedings of the CSEE, 2016, 36(7): 1760-1771.

[13] 赵聪, 李耀华, 李子欣, 等. 适合于柔性高压直流输电系统的模块化多电平变流器的自适应均压方法[J]. 电网技术, 2017, 41(5): 1510-1518.

ZHAO Cong, LI Yaohua, LI Zixin, et al. An adaptive voltage balancing method of modular multilevel converter for HVDC transmission systems[J]. Power System Technology, 2017, 41(5): 1510-1518.

[14] 刘国伟, 姜齐荣, 魏应冬. 低频率工况下模块化多电平变流器电容电压平衡控制策略[J]. 电工技术学报, 2014, 29(8): 166-172.

LIU Guowei, JIANG Qirong, WEI Yingdong. Study on capacitor voltage balancing control of modular multilevel converters at low frequency[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 166-172.

[15] ZHAO C, LI Y, LI Z, et al. An adaptive submodule voltage balancing method for modular multilevel converter in HVDC transmission system[C]// 2016 Conference of the IEEE Industrial Electronics Society. Kota Kinabalu: IEEE, 2016: 2514-2519.

[16] 赵昕, 赵成勇, 李广凯, 等. 采用载波移相技术的模块化多电平换流器电容电压平衡控制[J]. 中国电机工程学报, 2011, 31(21): 48-55.

ZHAO Xin, ZHAO Chengyong, LI Guangkai, et al. Sub-module capacitance voltage balancing of modular multilevel converter based on carrier phase shifted SPWM technique[J]. Proceedings of the CSEE, 2011, 31(21): 48-55.

[17] 申科, 王建赜, 班明飞,等. 基于阶梯波调制的MMC电容电压平衡控制方法对比研究[J]. 电机与控制学报, 2016, 20(10): 1-8.

SHEN Ke, WANG Jianze, BAN Mingfei, et al. Comparative analysis on capacitor voltage balance control strategies for staircase modulated modular multilevel converter [J]. Electric Machines and Control, 2016, 20(10): 1-8.

[18] 屠卿瑞. 模块化多电平换流器型直流输电若干问题研究[D]. 杭州: 浙江大学, 2013.

TU Qingrui. Research on several issues in modular multilevel converter based HVDC[D]. Hangzhou: Zhejiang University, 2013.

[19] 高建, 苏建徽, 高航, 等. 模块化多电平换流器电容电压与环流的控制策略[J]. 电力系统保护与控制, 2014, 42(3): 56-62.

GAO Jian, SU Jianhui, GAO Hang, et al. Capacitor voltage and circulation current control strategy in modular multilevel converter[J]. Power System Protection and Control, 2014, 42(3): 56-62.

[20] 魏晨华, 杨岩, 谢阳, 等. 模块化多电平变换器关键题研究综述[J]. 电子设计工程, 2014, 22(6): 182-186.

WEI Chenhua, YANG Yan, XIE Yang, et al. A review of key issues for modular multilevel converter[J]. Electronic Design Engineering, 2014, 22(6): 182-186.

[21] 苟锐锋, 赵方舟, 肖国春, 等. 基于修正优化归并排序的MMC电容均压策略[J]. 中国电机工程学报, 2017, 37(1): 251-261.

GOU Ruifeng, ZHAO Fangzhou, XIAO Guochun, et al. A capacitor voltage balancing strategy for MMC based on optimized merge sort[J]. Proceedings of the CSEE, 2017, 37(1): 251-261.

[22] 熊岩, 赵成勇, 许建中. 模块化多电平换流器电容电压均衡排序算法综述[J]. 电力工程技术, 2017, 36(2): 1-8.

XIONG Yan, ZHAO Chengyong, XU Jianzhong. A review of ranking algorithms for MMC capacitor voltages balancing[J]. Electric Power Engineering Technology, 2017, 36(2): 1-8.

[23] DONGARRA J. The top 10 algorithms[J]. IEEE Computing in Science amp; Engineering, 2002, 2(1): 22-23.

[24] CORMEN T, LEISERSON C, RIVEST R, et al. Introduction to algorithm[M]. Cambridge: MIT Press, 2009: 78-90.

[25] 焦晓鹏, 刘青. 基于改进快速排序算法的MMC均压控制策略[J]. 电力建设, 2017, 38(7): 146-152.

JIAO Xiaopeng, LIU Qing. Voltage balancing control strategy for modular multilevel converter based on improved quick sort algorithm[J]. Electric Power Construction, 2017, 38(7): 146-152.

[26] 粟时平, 魏新伟, 牛鼎, 等. 模块化多电平换流器电容电压改进排序平衡方法[J]. 中国电机工程学报, 2017, 37(13): 3874-3882.

SU Shiping, WEI Xinwei, NIU Ding, et al. A modified-sorting balancing method of capacitor voltage for modular multilevel converter[J]. Proceedings of the CSEE, 2017, 37(13): 3874-3882.

[27] 范丰, 粟时平, 刘桂英,等. 一种改进的模块化多电平换流器电压平衡方法[J]. 电力科学与工程, 2017, 33(4):13-19.

FAN Feng, SU Shiping, LIU Guiying, et al. An improved capacitor voltage balancing method for MMC based on radix sort [J]. Electric Power Science and Engineering, 2017, 33(4):13-19.

[28] ZHAO F, XIAO G, SONG Z, et al. Insertion sort correction of two-way merge sort algorithm for balancing capacitor voltages in MMC with reduced computational load[C]// 2016 IEEE 8thInternational on Power Electronics and Motion Control Conference (IPEMC-ECCE Asia). Hefei: IEEE, 2016: 748-753.

[29] ZHAO F, XIAO G, LIU M, et al. A fast sorting strategy based on a two-way merge sort for balancing the capacitor voltages in modular multilevel converters[J]. Journal of Power Electronics, 2017, 17(2): 346-357.

[30] SIEMASZKO D. Fast sorting method for balancing capacitor voltages in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 463-470.

[31] 常非, 杨晓峰, 贾海林, 等. 适用于现场可编程门阵列的MMC电容电压平衡控制方法[J]. 电网技术, 2015, 39(5): 1246-1253.

CHANG Fei, YANG Xiaofeng, JIA Hailin, et al. A capacitor voltage balance control algorithm for modular multilevel converter suitable to field programmable gate array [J]. Power System Technology, 2015, 39(5): 1246-1253.

[32] KUMAR M, HIRSCHBERG D S. An efficient implementation of Batcher’s odd-even merge algorithm and its application in parallel sorting schemes[J]. IEEE Transactions on Computers, 1983, 32(3): 254-264.

[33] MATAR M, PARADIS D, IRAVANI R. FPGA-based implementation of modular multilevel converter model for real-time simulation of electromagnetic transients[C]// 2013 International Conference on Power Systems Transients (IPST). Vancouver: Springer Berlin Heidelberg, 2013:18-20.

[34] MUELLER R. Sorting networks on FPGAs[J]. Vldb Journal, 2012, 21(1):1-23.

[35] RICCO M, MATHE L, TEODORESCU R. FPGA-based implementation of sorting networks in MMC applications[C]// 2016 European Conference on Power Electronics and Applications. Karlsruhe: IEEE, 2016: 1-10.

[36] 常非, 杨中平, 陈俊,等. 模块化多电平换流器电容电压平衡并行排序方法[J]. 高电压技术, 2016, 42(10): 3166-3171.

CHANG Fei, YANG Zhongping, CHEN Jun, et al.Parallel sorting method for capacitor voltage balancing of MMC[J]. High Voltage Engineering, 2016, 42(10): 3166-3171.

[37] 魏新伟, 粟时平, 邱欣, 等. 模块化多电平换流器电容电压新型优化平衡方法[J]. 电网技术, 2017, 41(3): 729-735.

WEI Xinwei, SU Shiping, QIU Xin, et al. A novel optimized capacitor voltage balancing method for modular multilevel converter[J]. Power System Technology, 2017, 41(3): 729-735.

[38] 俎立峰, 胡四全, 吉攀攀, 等. 一种高速MMC子模块均压算法[J]. 电力电子技术, 2015, 49(8): 86-88.

ZU Lifeng, HU Siquan, JI Panpan, et al. A high-speed non-sort algorithm MMC sub-module equalizing[J]. Power Electronics, 2015, 49(8): 86-88.

[39] RICCO M, MATHE L, TEODORESCU R. New MMC capacitor voltage balancing using sorting-less strategy in nearest level control[C]// 2016 IEEE Energy Conversion Congress and Exposition. Milwaukee: IEEE, 2016: 1-8.

[40] 林周宏, 刘崇茹, 李海峰, 等. 模块化多电平换流器的子模块电容电压分层均压控制法[J]. 电力系统自动化, 2015, 39(7): 175-180.

LIN Zhouhong, LIU Chongru, LI Haifeng, et al. A stratified voltage balancing control method of sub-module capacitor voltage for module multilevel converter[J]. Automation of Electric Power Systems, 2015, 39(7): 175-180.

[41] 赵成勇, 刘兴华, 王朝亮,等. 一种模块化多电平换流器的子模块分组均压控制方法: CN102916592A[P]. 2013-02-06.

[42] 彭茂兰, 赵成勇, 刘兴华, 等. 采用质因子分解法的模块化多电平换流器电容电压平衡优化算法[J]. 中国电机工程学报, 2014, 34(33): 5846-5853.

PENG Maolan, ZHAO Chengyong, LIU Xinghua, et al. An optimized capacitor voltage balancing control algorithm for modular multilevel converter employing prime factorization method[J]. Proceedings of the CSEE, 2014, 34(33): 5846-5853.

[43] 何智鹏, 许建中, 苑宾, 等. 采用质因子分解法与希尔排序算法的MMC电容均压策略[J]. 中国电机工程学报, 2015, 35(12): 2980-2988.

HE Zhipeng, XU Jianzhong, YUAN Bin, et al. A capacitor voltage balancing strategy adopting prime factorization method and shell sorting algorithm for modular multilevel converter[J]. Proceedings of the CSEE, 2015, 35(12): 2980-2988.

[44] 罗永捷, 李子欣, 李耀华, 等. 一种模块化多电平换流器分布式均压控制策略[J]. 电源学报, 2015, 13(6): 77-83.

LUO Yongjie, LI Zixin, LI Yaohua, et al.A distributed control method for voltage balancing in modular multilevel converters[J]. Journal of Power Supply, 2015, 13(6): 77-83.

[45] LUO Y, LI Z, LI Y, et al. A distributed control method for power module voltage balancing of modular multilevel converters[C]//2016 IEEE Energy Conversion Congress and Exposition. Milwaukee: IEEE, 2016:1-5.

[46] TU Q, XU Z. Impact of sampling frequency on harmonic distortion for modular multilevel converter[J]. IEEE Transactions on Power Delivery, 2010, 26(1): 298-306.

[47] 屠卿瑞, 徐政, 姚为正. 模块化多电平换流器型直流输电电平数选择研究[J]. 电力系统保护与控制, 2010, 38(20): 33-38, 44.

TU Qingrui, XU Zheng, YAO Weizheng.Selecting number of voltage levels for modular multilevel converter based HVDC[J]. Power System Protection and Control, 2010, 38(20): 33-38, 44.

[48] 喻锋, 王西田. 基于冒泡原理的模块化多电平换流器快速电压均衡控制策略[J]. 电力自动化设备, 2015, 35(9): 81-86.

YU Feng, WANG Xitian.Fast voltage balancing control based on bubbling principle for modular multilevel converter[J]. Electric Power Automation Equipment, 2015, 35(9): 81-86.

[49] LI W, GRÉGOIRE L A, BÉLANGER J. A modular multilevel converter pulse generation and capacitor voltage balance method optimized for FPGA implementation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2859-2867.

[50] 许烽, 徐政, 张哲任,等. 基于降损调制技术的全桥MMC电容电压无需排序均衡控制[J]. 电网技术, 2013, 37(12): 3347-3355.

XU Feng, XU Zheng, ZHANG Zheren, et al. Reduced loss modulation based capacitor voltage non-sorting balancing control for full-bridge MMC [J]. Power System Technology , 2013, 37(12): 3347-3355.

[51] ILVES K, HARNEFORS L, NORRGA S, et al. Predictive sorting algorithm for modular multilevel converters minimizing the spread in the submodule capacitor voltages[J]. IEEE Transactions on Power Electronics, 2014, 30(1):440-449.

[52] 姜喜瑞, 贺之渊, 汤广福, 等. 基于禁忌搜索优化算法的高压大容量柔性直流输电子模块电容电压平衡算法[J]. 中国电机工程学报, 2013, 33(21): 71-80.

JIANG Xirui, HE Zhiyuan, TANG Guangfu, et al.A capacitor voltage balancing control strategy for high-voltage large-capacity VSC-HVDC systems based on tabu search hard optimization algorithm[J]. Proceedings of the CSEE, 2013, 33(21): 71-80.

[53] LI Y, JONES E A, WANG F. The impact of voltage-balancing control on switching frequency of the modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2015, 31(4): 2829-2839.

[54] 潘武略. 新型直流输电系统损耗特性及降损措施研究[D]. 杭州: 浙江大学, 2008.

PAN Wulue. Loss evaluation and reduction approaches for VSC-HVDC systems[D]. Hangzhou: Zhejiang University, 2008.

[55] 徐政. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2016: 92-95.

[56] 黄守道, 廖武, 高剑, 等. 基于改进均压算法的模块化多电平变流器开关频率分析[J]. 电工技术学报, 2016, 31(13): 36-45.

HUANG Shoudao, LIAO Wu, GAO Jian, et al. Switching frequency analysis of modular multilevel converter based on the improved capacitor voltage balancing algorithm[J]. Transactions of China Electrotechnical Society. 2016, 31(13): 36-45.

[57] 屠卿瑞, 徐政, 郑翔, 等. 一种优化的模块化多电平换流器电压均衡控制方法[J]. 电工技术学报, 2011, 26(5): 15-20.

TU Qingrui, XU Zheng, ZHENG Xiang, et al. An optimized voltage balancing method for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 15-20.

[58] TU Q, XU Z, XU L. Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters[J]. IEEE Transactions on Power Delivery, 2011, 26(3):2009-2017.

[59] LI Z, GAO F, XU F, et al. Power module capacitor voltage balancing method for a ±350 kV/1 000 MW modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 3977-3984.

[60] 辛业春, 王朝斌, 李国庆, 等. 模块化多电平换流器子模块电容电压平衡改进控制方法[J]. 电网技术, 2014, 38(5): 1291-1296.

XIN Yechun, WANG Chaobin, LI Guoqing, et al. An improved balance control for sub-module capacitor voltage of modular multilevel converter[J]. Power System Technology, 2014, 38(5): 1291-1296.

[61] 喻锋, 王西田, 林卫星, 等. 一种快速的模块化多电平换流器电压均衡控制策略[J]. 中国电机工程学报, 2015, 35(4): 929-934.

YU Feng, WANG Xitian, LIN Weixing, et al. A fast voltage balancing control method for modular multilevel converter[J]. Proceedings of the CSEE, 2015, 35(4): 929-934.

[62] QIN J, SAEEDIFARD M. Reduced switching-frequency voltage-balancing strategies for modular multilevel HVDC converters[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2403-2410.

[63] 管敏渊, 徐政. MMC型VSC-HVDC系统电容电压的优化平衡控制[J]. 中国电机工程学报, 2011, 31(12): 9-14.

GUAN Minyuan, XU Zheng. Optimized capacitor voltage balancing control for modular multilevel converter based VSC-HVDC system[J]. Proceedings of the CSEE, 2011, 31(12): 9-14.

[64] 陆翌, 王朝亮, 彭茂兰,等. 一种模块化多电平换流器的子模块优化均压方法[J]. 电力系统自动化, 2014, 38(3): 52-58.

LU Yi, WANG Chaoliang, PENG Maolan, et al. An optimized method for balancing sub-module voltages in modular multilevel converters[J]. Automation of Electric Power Systems, 2014, 38(3): 52-58.

[65] 郭裕群, 赵成勇, 许建中,等. 模块化多电平换流器子模块平均开关频率的精确控制方法[J]. 电力系统自动化, 2016, 40(19): 94-100.

GUO Yuqun, ZHAO Chengyong, XU Jianzhong, et al. Precision control method of average sub-module switching frequency for modular multilevel converters[J]. Automation of Electric Power Systems, 2016, 40(19): 94-100.

2017-05-05

王坤(1993)，男，硕士研究生，主要从事柔性直流输电运行与控制等方面的研究工作；

刘开培(1962)，男，教授，博士生导师，主要从事新能源与智能电网等方面的研究工作；

王思茹(1994)，女，硕士研究生，主要从事光伏发电并网等方面的研究工作;

李威(1976)，男，高级工程师，主要从事大电网安全稳定性分析等方面的研究工作;

王玉(1988)，女，工程师，主要从事电网安全稳定分析等方面的研究工作；

冉晓洪(1984)，男，通信作者，博士，主要从事电力系统保护与控制等方面的研究工作。

(编辑 郭文瑞)

ComparativeAnalysisonMMCCapacitorVoltageBalancingStrategyBasedonSortingAlgorithm

WANG Kun1, LIU Kaipei1, WANG Siru1, LI Wei2, WANG Yu2, RAN Xiaohong1

(1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China;
2. NARI Group Corporation(State Grid Electric Power Research Institute), Nanjing 210003, China)

Capacitor voltage balancing control strategy based on sort algorithm for modular multilevel converter (MMC) is widely used in practical engineering because of its good response to voltage balance. However, the real-time sorting requires excessive computation and high-frequency switching actions will result in larger switching losses. Therefore, while maintaining the module voltage balance, more research should be contributed to the time complexity and switching frequency of the balancing strategy. Based on the research of voltage balancing strategy of conventional sort algorithm, the existing improved strategies are divided into 3 categories according to different optimization mechanisms. The 3 kinds of strategies are compared and analyzed through different evaluation indexes. Finally, this paper discusses the future research direction and development trend of MMC voltage balancing strategy, which can provide reference and guidance for solving the capacitor voltage imbalance of MMC.

modular multilevel converter(MMC); voltage balancing strategy; sort algorithm; time complexity; switching frequency

国家自然科学基金项目(51607125)；中央高校基本科研业务费专项资金资助项目(2042016kf1048)

Project supported by National Natural Science Foundation of China(51607125); Fundamental Research Funds for the Central Universities(2042016kf1048)

TM46

A

1000-7229(2017)11-0009-10

10.3969/j.issn.1000-7229.2017.11.002