基于交替方向乘子法的源网协同多适应规划

李婷，叶希，唐权，王云玲，瞿小斌，文云峰

(1.国网四川省电力公司经济技术研究院，成都市 610041；2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆市 400044)

基于交替方向乘子法的源网协同多适应规划

李婷1，叶希1，唐权1，王云玲1，瞿小斌2，文云峰2

(1.国网四川省电力公司经济技术研究院，成都市 610041；2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆市 400044)

电源规划与电网规划紧密相关，有必要考虑其相互影响进行协同规划。该文兼顾分布式决策环境与多适应性条件，提出了一种电源与电网协同的多适应规划框架，利用交替方向乘子法(alternating direction method of multipliers，ADMM)分别构建了耦合共享变量的电源规划决策子问题与电网规划决策子问题，2个子问题相互通信、交替求解，实现了电源与网架协同的分布式自治规划。该框架和方法保留了决策主体信息的私密性，同时确保了电源规划方案和电网规划方案所构成的整体系统的经济性和适应性。在Garver-6系统上对该文方法的有效性进行了验证。

电源规划；电网规划；交替方向乘子法(ADMM)；协同；分布式

0 引 言

电源规划和电网规划是电力规划的主要内容[1]。电源规划对电源布局进行战略决策，根据规划时间尺度内的负荷预测，在满足技术合理性和考虑多种类电厂相互协调的前提下寻求最经济的电源发展方案，主要确定在何时何地投建何种类型和多大容量的机组[2]。电网规划是在给定负荷预测和电源规划方案的基础上，确定投资和运行费用最小的网架扩展规划方案，主要解决何时何地新建多少线路以适应电力供需变化的问题[3]。

传统经验型的电力系统规划一般将电源与电网规划分割考虑：由负荷及资源确定电源，由电源确定电网，串序进行电源规划和电网规划[4]。这种高度独立的方式所确定的网源裕度配合方案可能造成电源和电网规划不协调的现象，如电源冗余度过高或电网安全水平过低。由于电源规划和电网规划的决策执行方案紧密相关，为确保规划系统在未来的安全、可靠、经济和高效运行，有必要考虑电源和电网规划方案的相互作用和影响，制定具有多适应性的源网协同最优规划方案[5-6]。

然而，在“厂网分开，竞价上网”的电力市场环境下，电厂与电网分别成立了独立的发电公司和具有自然垄断地位的电网公司。由于发电公司和电网公司分属不同利益的决策主体，使得电源规划和电网规划相互独立，从根本上改变了原始垂直一体化电力系统规划的理念，增加了电源与电网协同规划的难度和不确定性[7]。另一方面，在近年来我国清洁能源基地大规模建设与发展的过程中，配套网架规划和建设相对脱节和滞后，局部地区弃风、弃光、弃水限电问题严重[8]，进一步凸显电源规划和电网规划协同的紧迫性。

近年来，电源与电网协同规划的研究已逐渐引起国内外学者的重视。文献[9]提出了电源电网协调规划模型，着重考虑了调节型电源的装机规划与输电线路选址问题。文献[10]从可靠性均衡角度，提出一种利用虚拟机组进行源网协调规划的方法。文献[11]通过线路容量限制修正电源规划方案以寻求电源与电网规划的协调。文献[12]针对风电场接入系统与输电网扩展的协调规划问题，建立了2步式电网扩展规划综合模型，寻求综合效益最优的规划方案。然而，这些研究将电源和电网2个独立规划问题的目标函数和约束条件统一到同一个优化模型中，形成源网集成大规模规划模型。该模型与厂网分开、分布决策的市场环境不符，破环了决策主体本体信息的私密性。此外，若考虑投资、技术、环保和政策等纷繁复杂的适应性约束，模型将过于庞大，求解困难。

本文提出一种兼顾分布式决策环境的源网协同多适应规划框架，利用交替方向乘子法构建电源规划决策主体与电网规划决策主体的分布式协同互动交互机制和优化求解流程。该框架和方法保留决策主体信息的私密性，同时确保电源规划方案和电网规划方案所构成的整体系统的经济性和适应性。

1 电源与电网协同的多适应规划框架

区别于源网集成统一规划方式，本文所建立的源网协同规划方法立足“厂网分开”竞争市场环境，充分考虑了电源规划中心与电网规划中心的协同和互动，实现分布自治决策，其框架如图1所示。该分布式协同规划框架的特点如下详述。

(1) 电源规划中心和电网规划中心分别构建耦合共享变量的电源规划模型和电网规划模型，各自在满足投资、技术、环保和政策等多适应性约束的前提下自治决策本体最优的规划方案；

(2) 电源规划中心与电网规划中心2个决策主体间通过少量多次的信息传递(共享变量和价格信号)和迭代计算(规划方案校核与更新)，达到电源规划与电网规划分布自治决策、协同实现全系统最优多适应规划。

图1 电源与电网协同的多适应规划框架Fig.1 Framework of synergistic adaptive planning ofgeneration and transmission

发电机组有功功率为电源在电网中的表现形式，是电源规划问题和电网规划问题的共享变量。共享变量既满足电源规划问题所有约束又满足电网规划问题所有约束，将电源规划和电网规划进行耦合，有效保证数据的私密性和规划方案的可行性。

在电源规划和电网规划分布式协同交互过程中须满足如下一致性关系式：

(1)

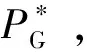
2 ADMM算法简介

交替方向乘子法(alternating direction method of multipliers, ADMM)是一种求解分布式优化问题的算法。ADMM通过分解协调机制，将大规模全局优化问题分解为多个小规模子问题，通过子问题协调通信求解得到全局问题的最优解。其具有形式简单，收敛性好，鲁棒性强等优点，是近年来获得广泛应用的分布式数学优化方法[13-15]。由于ADMM算法能够保留决策主体的数据保密性并显著降低计算规模，因此适用于电源规划与电网规划的分布自治决策和互动协同。

其算法形式简述如下：

minH(x,z)=f(x)+g(z)

(2)

s.t.Axc+Bzc=C

(3)

式中：H(x,z)表示全局优化问题目标函数；f(x)、g(z)为全局问题拆分的2个子问题的目标函数；x、z分别为“X子问题”和“Z子问题”的变量，x∈Rn，z∈Rm；xc、zc为共享变量；A、B、C为共享变量的约束矩阵，A∈Rp×n，B∈Rp×m，C∈Rp。

将耦合约束式(3)加入原目标函数构造如下的计及约束的目标函数Lω(x,z,y)：

Lω(x,z,y)=f(x)+g(z)+

(4)

式中：λ为乘子向量；ω为常数惩罚因子；‖·‖2为2范数算子。

式(4)将耦合约束转换到目标函数中，为原问题的拆分及分布式求解提供了契机。

将式(4)中1个子问题的共享变量作为已知量进行拆分得到迭代方程，由此全局问题拆分为多个子问题。迭代方程为

(5)

式(5)求解过程如下：首先，“X子问题”处于计算状态，待计算完成将共享变量传递至“Z子问题”，并处于待命状态，之后等待“Z子问题”计算完成后传回共享变量。完成1轮求解后2个子问题按照式(6)更新乘子变量λ，并转入下一轮优化计算。

乘子向量的迭代公式为

(6)

式中λk为第k次迭代计算后变量λ的值。

ADMM算法收敛判据由2部分组成：

(7)

(8)

式中：rk+1、sk+1分别为第k+1次迭代计算后的原始残差和对偶残差；ρ为对偶残差公式系数；εpri、εdual分别为原始残差和对偶残差的容忍上限。

3 基于ADMM分布式算法的源网协同多适应性规划

以规划水平年整个电力系统投资成本及运行成本最低为目标，考虑风电出力、负荷持续曲线的多场景运行方式，计及基态线路潮流约束和N-1安全约束，基于ADMM算法构建相互耦合的电源规划子问题和电网规划子问题。2个子问题相互通信、交替求解，实现电源与网架的协同规划。本文采用文献[16-17]所述区间分析法考虑风电出力的不确定性。

3.1 电源规划子问题

耦合共享变量的电源规划子问题目标函数为

(9)

电源规划子问题需满足的多种适应性约束条件如下详述。

(1)常规发电机出力上、下限约束。

(10)

(11)

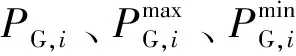
(2)风电场出力约束。

(12)

(3)机组爬坡约束。

(13)

(14)

(15)

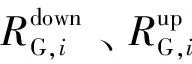
式(13)为机组在相邻时段平行场景下的爬坡约束；式(14)、(15)为风电出力在相邻时段极端上、下限间波动(s2、s3场景间相互转换)时系统内其他常规机组的爬坡约束。

(4)电力平衡约束。

(16)

式中PD,t为t时刻与电源相连电网总负荷。

(5)根据文献[18],可以确定负荷正、负备用约束。

(17)

(18)

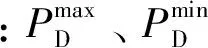
(6)火电燃料消耗约束。

(19)

式中：βi、Ui分别为第i台发电机组平均燃料单耗及燃料消耗限量；ΩH为火电机组集合。

(7)系统污染物排放约束。

(20)

式中γi、Vi分别为第i台发电机组污染物排放系数及最大污染排放量。

3.2 电网规划子问题

耦合共享变量的电网规划子问题目标函数为

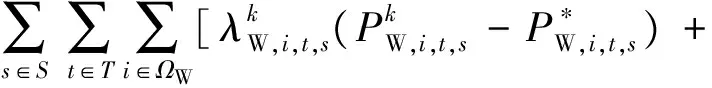
(21)

电网规划子问题需满足的多种适应性约束条件如下详述。

(1)节点功率平衡约束。

(22)

式中：NL为与节点q相连的支路集合；NG、NW分别为与节点q相连的常规发电机集合和风电场集合；Fl,t,s为s场景下与节点q相连的第l条支路在t时刻的功率；PD,q,t为节点q在t时刻的有功负荷。

(2)线路输送功率约束。

(23)

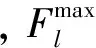
(3)潮流方程约束。

现有线路潮流计算等式和选中线路潮流计算等式为：

θA,l,t,s-θB,l,t,s=xlFl,t,s,l∈ΨE,t∈T,s∈S

(24)

θA,l,t,s-θB,l,t,s=xlFl,t,s,l∈ΨC,t∈T,s∈S,ZL,l=1

(25)

式中：θA,l,t,s、θB,l,t,s为s场景下t时刻线路l首、末两端电压相角；xl为线路l的电抗。

式(25)虽有线性表述形式，但实则只有在ZL,l=1时才成立，因此，对其做如下线性化处理[19]：

-E(1-ZL,l)≤(θA,l,t,s-θB,l,t,s)-xlFl,t,s≤

E(1-ZL,l) ,l∈ΨC,t∈T,s∈S

(26)

式中：E为一个很大的常数。

分析式(26)可以看出：当ZL,l=1时，式(26)简化为该线路的潮流方程；当ZL,l=0时，结合线路传输功率约束式(23)可确定线路潮流为0。

(4)N-1安全约束。

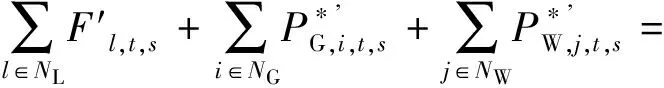
(27)

(28)

(29)

(30)

(31)

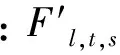
(5)基态、N-1状态关联约束。

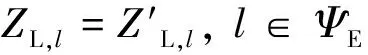
(32)

式中：φ表示N-1故障线路。

关联约束保证了在任意N-1故障情况下线路规划方案同基态线路规划方案一致。

3.3 源网协同规划算法流程

基于ADMM算法的电源、电网分布式协同规划求解流程如下详述。

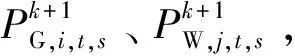
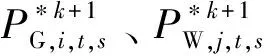
步骤4按式(33)、(34)更新乘子系数：

(33)

(34)

步骤5根据式(7)、(8)判断收敛性，若收敛判据成立，则停止计算输出结果，否则迭代次数k加1，并转至步骤2开始下一次分布式自治优化计算。

4 算例分析

在Windows 8系统Intel(R) Core(TM) i5-6500 CPU(3.2 GHz)和16 GB的电脑上利用Matlab 2015a平台编写基于ADMM的源网协同规划算法程序，调用CPLEX 12.7优化包辅助求解。以Garver-6电力系统规划为测试算例，与非协同规划结果进行了对比，验证开展协同规划的必要性；并与集中式规划结果进行对比，以说明本文所提方法的有效性。

为满足电力系统规划计算，本文对Garver-6系统稍作修改，计划在节点K1处增设待选常规电源G3、风电W1，在节点K4处增设待选常规电源G4，网络中增加待选线路L6-L8，具体结构如图2所示。假定风电出力不确定性取±20%的波动幅度[17]，所有线路潮流限值为250 MW。

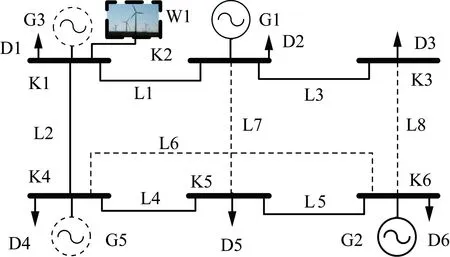
图2 Garver-6电力系统规划结构图Fig.2 Planning structure of Garver-6 power system

4.1 原始潮流结果

进行机组及线路扩建前，列出电源最大有功出力及电网最大有功负荷，具体见表1。规划前系统在最大负荷下的发电机出力及线路潮流曲线如图3、4所示。09:00—24:00，电源G1、G2基本处于满载状态，线路L5会出现潮流越限情况。若考虑N-1故障，形势将更加严峻，急需对电源及线路进行扩建。

表1机组容量及节点最大负荷情况
Table1Capacityofgeneratorsandmaximumnodesload

图3 规划前发电机组出力曲线Fig.3 Power output curve of pre-planning

4.2 非协同规划结果

考虑非协同规划(源网分割、串序规划)情况所得结果见表2(其中电源状态和线路状态：“1”表示投建，“0”表示不投建)。电源规划选择新增建设W1，电网规划结果新增建设线路L6-L8，规划后网络结构如图5所示，图中虚线代表新增建设电源或输电线路。该规划方案将所有待选线路扩建，电网建设费用CN较高，为2.000 0×107$，对应的电源建设及运行费用CG为3.061 8×107$，规划水平年源网建设及运行总费用CT为5.061 8×107$。

图4 规划前线路潮流曲线Fig.4 Power flow curve of pre-planning

表2非协同规划方案
Table2Resultofnon-synergisticplanning

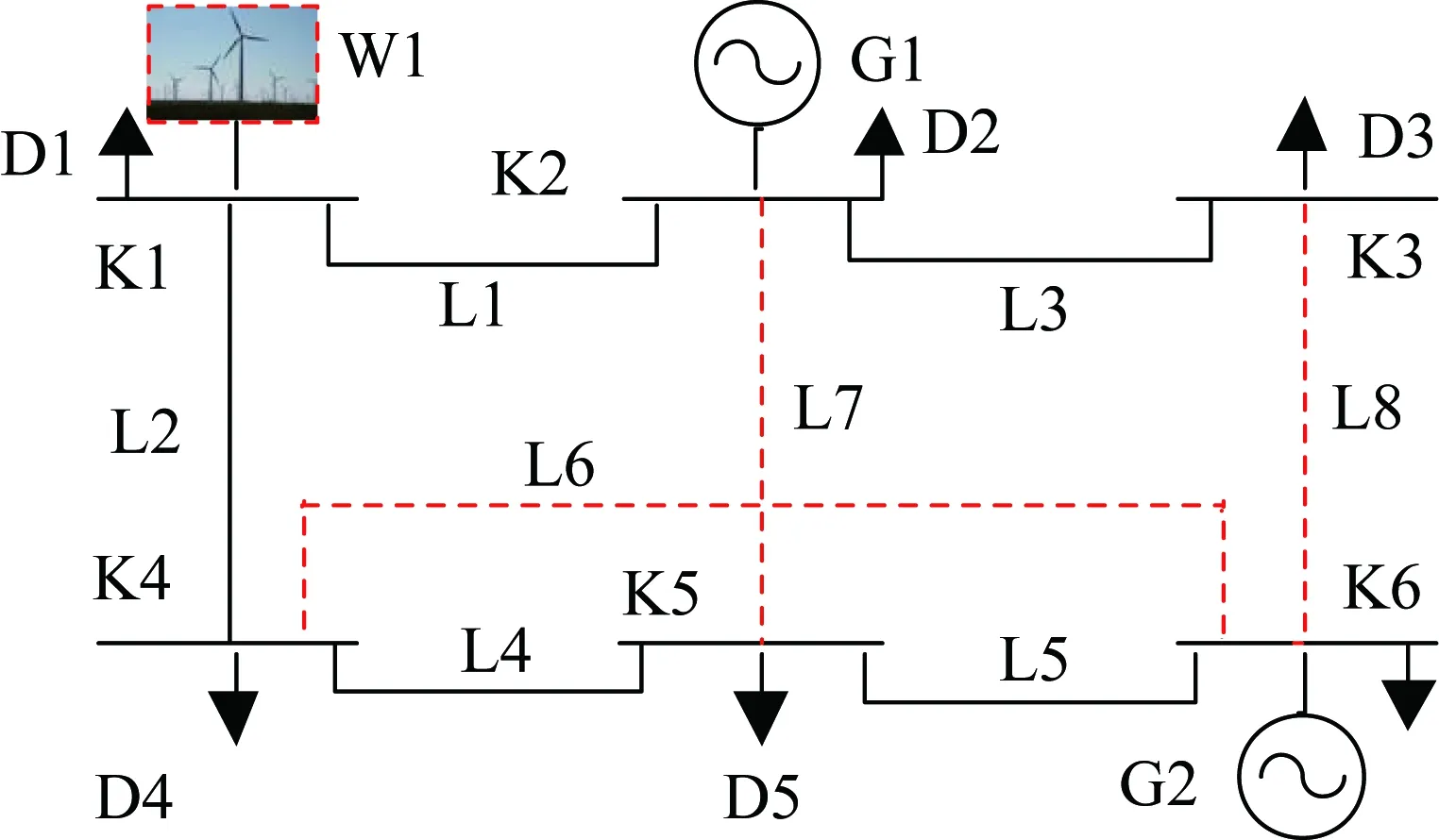
图5 Garver-6非协同规划后网络结构Fig.5 Garver-6 network structure ofnon-synergistic planning

4.3 协同规划结果

采用本文所提基于ADMM的源网分布式协同规划算法进行协同规划计算。ADMM计算所需参数及初值设定见表3，ADMM分布式协同规划和集中式协同规划(电源和电网2个独立规划问题的目标函数和约束条件集成到同一个优化模型中)的计算结果见表4。其中，N为迭代次数，t为求解耗时。可以看出，集中式和ADMM分布式2种方法均得出了W1、G3、L7、L8投建，G4、L6不投建的规划方案，且2种模型计算所得的规划水平年源网总费用均为4.146 8×107$，说明基于ADMM的源网分布式协同规划可达到与集中式统一源网规划模型同样精度的计算结果。虽然集中式协同规划计算耗时较少，但该方法与实际中“厂网分开”的电力市场管理模式不符(电厂与电网分属不同的利益决策主体)。分布式协同规划解决了集中式方法信息传递量大、信息私密性差等重要问题，因而更具有实际意义。此外，由于本文是在单机环境中运行分布式协同规划的计算程序，若采用多台计算机构建的分布式计算资源，将有望有效提升计算效率。

规划后网络结构如图6所示，图中虚线代表新增电源或输电线路。相较于非协同规划扩建1台机组和3条线路的方案，协同规划方案采取扩建2台机组和2条线路的方案，整体经济性更佳。

表3ADMM计算参数及初值
Table3ParameterandinitialvaluesofADMMcalculation

表4 协同规划方案Table 4 Result of synergistic planning

图6 Garver-6协同规划后网络结构Fig.6 Garver-6 network structure of synergistic planning

对比了非协同规划、协同规划2种方案的费用情况，如图7所示。由图7所知，协同规划的总费用CT=4.146 8×107$，相较5.061 8×107$的非协同规划总费用降低了18.1%，经济性优于非协同规划方案。这是因为，非协同方式下，电源规划仅考虑电源投建及运行费用最低，得到CG=3.061 8×107$，低于协同规划方案的电源投资及运行费用 (3.146 8×107$)，但由于电源规划与电网规划相互分割、串序执行，导致电网规划的费用(2.000 0×107$)远高于协同规划方式下的费用(1.000 0×107$)。综上所述，因协同规划方案的全局最优性，使得协同规划的源网投资及运行费用低于非协同规划情况。

图7 非协同规划、协同规划费用对比Fig.7 Cost comparison of non-synergistic andsynergistic planning

ADMM分布式源网协同规划计算过程中的费用收敛曲线如图8所示。由于迭代过程中电源及电网2个规划子问题的共享变量(发电机组有功功率)相互协调、逐渐趋于相等，使得总的投资及运行费用逐渐降低直至收敛。惩罚因子ω变化对ADMM算法计算性能的影响见表5，可以看出ω的取值对ADMM算法收敛速度有一定影响，在本算例情况下ω的最佳取值为35。

图8 规划水平年费用收敛曲线Fig.8 Convergence curves of planning level year costs

5 结 论

(1)提出了一种兼顾分布式决策环境的源网协同多适应规划框架，解决了电源规划与电网规划不匹配问题，改善了规划方案的经济性。

(2)基于ADMM构建了电源规划决策主体与电网规划决策主体的分布式协同交互问题和实现流程，在保留决策主体信息的私密性的同时可得到与集中式源网规划一致的规划结果，确保了分布协同规划的经济性和适应性。

在下一步工作中将研究考虑系统暂态稳定性的更为完善的源网协同分布式多适应规划模型，并进一步探索提高分布式源网协同规划求解效率的计算方法。

[1] 程浩忠. 电力系统规划 [M]. 第2版.北京: 中国电力出版社, 2014:73-95, 121-154.

[2] 范彬, 周力行, 黄頔,等. 基于改进蝙蝠算法的配电网分布式电源规划[J]. 电力建设, 2015, 36(3):123-128.

FAN Bin, ZHOU Lixing, HUANG Di, et al. Distributed generation planning for distribution network based on modified bat algorithm[J]. Electric Power Construction, 2015, 36(3):123-128.

[3] 程耀华, 张宁, 康重庆,等. 考虑需求侧管理的低碳电网规划[J]. 电力系统自动化, 2016, 40(23):61-69.

CHENG Yaohua, ZHANG Ning, KANG Chongqing, et al. Low carbon transmission expansion planning considering demand side management[J]. Automation of Electric Power Systems, 2016, 40(23):61-69.

[4] 王锡凡. 电力系统优化规划[M]. 北京: 水利电力出版社, 1990: 223-224, 268-269.

[5] 张宁, 胡兆光, 周渝慧, 等. 计及随机模糊双重不确定性的源网荷协同规划模型[J]. 电力系统自动化, 2016, 40(1): 39-44.

ZHANG Ning, HU Zhaoguang, ZHOU Yuhui, et al. Soure-grid-load coordinated planning model considering randomness and fuzziness[J]. Automation of Electric Power Systems, 2016, 40(1): 39-44.

[6] 魏刚, 范雪峰, 张中丹, 等. 风电和光伏发展对甘肃电网规划协调性的影响及对策建议[J]. 电力系统保护与控制, 2015, 43(24): 135-141.

WEI Gang, FAN Xuefeng, ZHANG Zhongdan, et al. Influence of wind power and photovoltaic’s development on Gansu power grid planning coordination and suggestions[J]. Power System Protection and Control, 2015, 43(24): 135-141.

[7] 吉兴全, 文福拴. 电力市场环境下发电和输电规划协调问题综述[J]. 电力技术经济, 2008, 20(3): 18-23.

JI Xingquan, WEN Fushuan. Summary on coordinated investment and planning for generation and transmission sectors in power market environment[J]. Electric Power Technologic Economics, 2008, 20(3): 18-23.

[8] 郭永明, 刘观起. 计及弃风成本的含抽水蓄能电力系统随机优化调度[J]. 电力建设, 2016, 37(4):29-34.

GUO Yongming, LIU Guanqi. Stochastic optimization scheduling method for pumped storage power system considering wind curtailment cost[J]. Electric Power Construction, 2016, 37(4):29-34.

[9] 高赐威, 吴天婴, 何叶, 等. 考虑风电接入的电源电网协调规划[J]. 电力系统自动化, 2012, 36(22): 30-35.

GAO Ciwei, WU Tianying, HE Ye, et al. Generation and transmission coordinated planning considering wind power integration[J]. Automation of Electric Power Systems, 2012, 36(22): 30-35.

[10] 穆永铮, 鲁宗相, 周勤勇, 等. 基于可靠性均衡优化的含风电电网协调规划[J]. 电网技术, 2015, 39(1): 16-22.

MU Yongzheng, LU Zongxiang, ZHOU Qinyong, et al. Optimized reliability balancing based transmission coordinating expansion planning for power grid with wind farms[J]. Power System Technology, 2015, 39(1): 16-22.

[11] GU Y, MCCALLEY J D, NI M. Coordinating large-scale wind integration and transmission planning[J]. IEEE Transactions on Sustainable Energy, 2012, 3(4): 652-659.

[12] 王秀丽, 张凯, 曾平良, 等. 基于多场景的风电场接入与输电网协调规划[J]. 电力建设, 2015, 36(10): 46-52.

WANG Xiuli, ZHANG Kai, ZENG Pingliang, et al. Coordinated planning of wind farm integration and transmission network based on multi-scenario[J]. Electric Power Construction, 2015, 36(10): 46-52.

[13] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations amp; Trends® in Machine Learning, 2011, 3(1):1-122.

[14] WEN Y F, QU X B, LI W Y, et al. Synergistic operation of electricity and natural gas networks via ADMM[J/OL]. IEEE Transactions on Smart Grid, (2017-02-02)[2017-03-01]. https://doi.org/10.1109/TSG.2017.2663380.

[15] 瞿小斌, 文云峰, 叶希, 等. 基于串行和并行ADMM算法的电-气能量流分布式协同优化[J]. 电力系统自动化, 2017, 41(4): 12-19.

QU Xiaobin, WEN Yunfeng, YE Xi, et al. Distributed optimization of gas-electric integrated energy flows using serial and parallel iterative modes for alternating direction method of multipliers[J]. Automation of Electric Power Systems, 2017, 41(4): 12-19.

[16] PANDZIC H, DVORKIN Y, WANG Y, et al. Toward cost-efficient and reliable unit commitment under uncertainty[C]// Power and Energy Society General Meeting (PESGM), IEEE, 2016.

[17] WEN Y F, LI W Y, HUANG G, et al. Frequency dynamics constrained unit commitment with battery energy storage [J]. IEEE Transactions on Power Systems, 2016, 31(6):5115-5125.

[18] 罗金山, 路畅, 孟繁骏. 碳排放及燃煤约束下的电源规划及其效益评价[J]. 电力系统自动化, 2016, 40(11):47-52.

LUO Jinshan, LU Chang, MENG Fanjun. Generation expansion planning and its benefit evaluation considering carbon emission and coal supply constraints[J]. Automation of Electric Power Systems, 2016, 40(11):47-52.

[19] 洪绍云, 程浩忠, 曾平良, 等. 基于相关场景聚类的发输电联合扩展规划[J]. 电力系统自动化, 2016, 40(22):71-76.

HONG Shaoyun, CHENG Haozhong, ZENG Pingliang, et al. Coordinated generation and transmission expansion planning with clusters of correlative scenarios[J]. Automation of Electric Power Systems, 2016, 40(22):71-76.

2017-05-02

李婷(1979)，女，学士，高级工程师，主要研究方向为电力系统规划；

叶希(1987)，女，博士，工程师，主要研究方向为电力系统规划、新能源并网分析与控制；

唐权(1982)，男，硕士，高级工程师，主要研究方向为电力系统规划；

王云玲(1979)，男，硕士，高级工程师，主要研究方向为电力系统规划；

瞿小斌(1993)，男，硕士研究生，主要研究方向为综合能源网、电力系统规划与优化运行；

文云峰(1986)，男，博士，讲师，主要研究方向为综合能源网、电力系统规划与优化运行。

(编辑 郭文瑞)

SynergisticAdaptivePlanningofGenerationandTransmissionUsingADMM

LI Ting1, YE Xi1, TANG Quan1, WANG Yunling1, QU Xiaobin2, WEN Yunfeng2

(1. Sichuan Power Economic Research Institute, Chengdu 610041, China; 2. State Key Laboratory of Power Transmission Equipment and System Security and New Technology, Chongqing University, Chongqing 400044, China)

Generation and transmission expansion planning interact with each other tightly, it is necessary to take the interaction into account when making planning. This paper proposes an adaptability planning framework of generation and transmission network by taking distributed decision environment and adaptability condition into consideration, and uses alternating direction method of multipliers (ADMM) to separately construct the decision-making sub-problems of generation planning and network planning with shared variable coupling. The two sub-problems communicate with each other and solve alternatively, which can realize the distributed synergy between generation and transmission network. The framework and approach keep information privacy and remain the economy and adaptability of the whole power system consisting of generation planning and network planning. Case studies based on the Garver-6 power system demonstrates the effectiveness and feasibility of the proposed approach.

generation planning; transmission planning; ADMM; synergy; distributed

国家电网公司科技项目(SGSCJY00JHJS1600024)；国家自然科学基金项目(51707017)；中央高校基本科研业务费专项资金资助项目(106112016CDJXY150002)；重庆市基础科学与前沿技术研究专项(cstc2017jcyjAX0422)

Project supported bythe Science and Technology Project of State Grid Corporation of China(SGSCJY00JHJS1600024)；National Natural Science Foundation of China(51707017)；Fundamental Research Funds for the Central Universities(106112016CDJXY150002 );Chongqing Research Program of Basic Research and Frontier Technology (cstc2017jcyjAX0422)

TM732

A

1000-7229(2017)11-0105-08

10.3969/j.issn.1000-7229.2017.11.014