振动拉削双阀激振系统输出波形稳定性分析及实验研究

蒙 臻， 倪 敬， 武传宇

(1. 杭州电子科技大学 机械工程学院，杭州 310018； 2. 浙江理工大学 机械与自动控制学院，杭州 310018)

振动拉削双阀激振系统输出波形稳定性分析及实验研究

蒙 臻1， 倪 敬1， 武传宇2

(1. 杭州电子科技大学 机械工程学院，杭州 310018； 2. 浙江理工大学 机械与自动控制学院，杭州 310018)

为了分析振动拉削系统在加工过程中电液激振输出幅值稳定性问题，首先引入流量耦合线性模型和拉削负载力模型，构建了双阀激振系统的传递函数，推导了系统输出位移和输出力的时域响应函数；再利用MATLAB仿真计算及绘制开环系统的Bode图和幅值时域响应曲线；最后，利用自行研制的振动拉削实验平台所测得的激振器输出幅值与仿真结果进行对比分析，研究结果表明：激振信号的频率会影响输出波形的平衡位置及波动幅值，激振信号频率越高，输出波形越容易调节；而拉削负载力主要影响输出波形的振荡次数，负载力越大，输出波形越不稳定。因此，为了使拉削过程中激振输出波形更加稳定，一方面可适当提高激振缸缸径和行程的比值，以增大系统极限响应频率，另一方面需蓄能装置或大流量型开关阀平衡激振缸容腔压力配比。

振动拉削；电液激振；Bode图；波形稳定性

振动拉削加工系统，最早由日本的隈部淳一郎教授公开发表[1]，可有效利用刀具与工件的脉冲式接触改善加工质量，提升加工效率，但所采用的机械式激振系统会导致严重的冲击效应，易划伤工件及损坏拉刀刀齿。所研制的双阀振动拉削系统通过流体驱动激振装置，具有较好的缓冲特性，可降低冲击对拉刀的损伤。分析加工过程中能否输出稳定的周期性波形，即探明影响电液激振系统输出稳定性的主要因素，对优化振动拉削系统参数，实现振动拉削加工工艺，提高拉削系加工性能，具有十分重要的理论和实际意义。

目前关于振动拉削公开发表的文献较少，但已有许多学者针对电液系统输出稳定性开展研究，先后发表了相关的理论分析和实验研究成果。如余洋等[2]通过模型理论分析和仿真计算，重点考虑了结构刚度对结晶器激振系统稳定性的影响；姜万录等[3]侧重于研究液压缸非线性刚度和摩擦力对电液系统稳定性的影响；葛振亮等[4]从管路的动态特性出发研究车辆液压转向系统的稳定性；金智林等[5]综合考虑多种系统因素作用下对所研制的新型汽车电液制动系统稳定性的影响；滕韬等[6-7]考虑了负载的冲击和阻尼效应对盾构刀盘驱动系统稳定性的影响；王爱国[8]通过非线性系统的李雅普诺夫判据判断矫直机液压伺服系统的稳定性； Amirante等[9]在研究液压阀的过程中，采用流体仿真软件分析了空穴效应对电液系统稳定性的影响； Yang等[10-13]则从反馈系统的角度，探讨电液激振系统的稳定性问题。但上述文献所涉及的研究内容，只探讨了液压控制系统的闭环稳定性，与输入方式及外界扰动关系不大，而振动拉削过程中，激振系统稳定性对拉削负载较为敏感，无法忽视输出响应的动态特性。因此，振动拉削电液激振系统在拉削负载耦合特性影响下的输出波形稳定性还有待于进一步研究。

本文以振动拉削电液激振系统为研究对象，通过引入流量耦合线性模型和拉削力模型，构建了激振系统传递函数模型和时域响应函数模型，采用MATLAB仿真计算和实际系统测试相结合的方法，研究了空载及负载下激振系统的稳定特性及其影响因素，为振动拉削工艺相关参数提供了优化方向。

1 振动拉削系统原理

普通拉削系统主要通过溜板及刀夹头，连接拉刀及主油缸，使拉刀在拉削行程内直线运动；而所研制的振动拉削系统如图1所示，将原拉削系统的溜板与刀夹头分离，并附加双阀电液激振装置，使拉刀在拉削直线运动时，复合了周期性直线往复运动特性。附加振动装置设计目标是产生稳定的大于切削速度vc的振动速度vt，其中vt=2πfa>vc，f为振动频率，a为振幅。

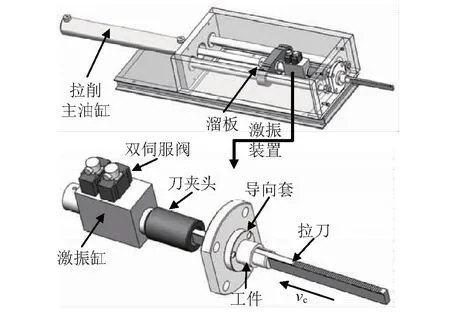
图1 振动拉削系统示意图Fig.1 Schematic diagram of vibration broaching system

本文所采用的电液激振装置，主要由双伺服阀以及模块式激振缸等组成。其中，激振缸缸体后端直接与拉床主油缸活塞杆头部螺纹连接，激振缸活塞杆直接与拉刀夹头螺纹连接，而刀夹头与拉刀则通过紧定插销和紧定螺栓连接。振动拉削系统工作原理为：通过主运动vc和振动运动vt的复合运动形式，将传统的接近→接触→拉削过程转换为接近→接触→拉削→脱离→再接近的脉冲式拉削过程。

2 激振系统特性分析

如图1所示的电液激振装置，将拉刀等负载等效为集中质量体后如图2所示，根据牛顿动力学方法，电液激振系统的动力学特性可描述为

(1)

式中：M为拉刀的质量，kg；m为刀夹头，活塞及活塞杆的总质量，kg；C为电液激振系统的总阻尼系数；K为系统的等效弹簧刚度；Fp为液压油流体激振力，N；Fc为拉削负载力，N；Ff为摩擦力，N；xp为活塞位移，mm。

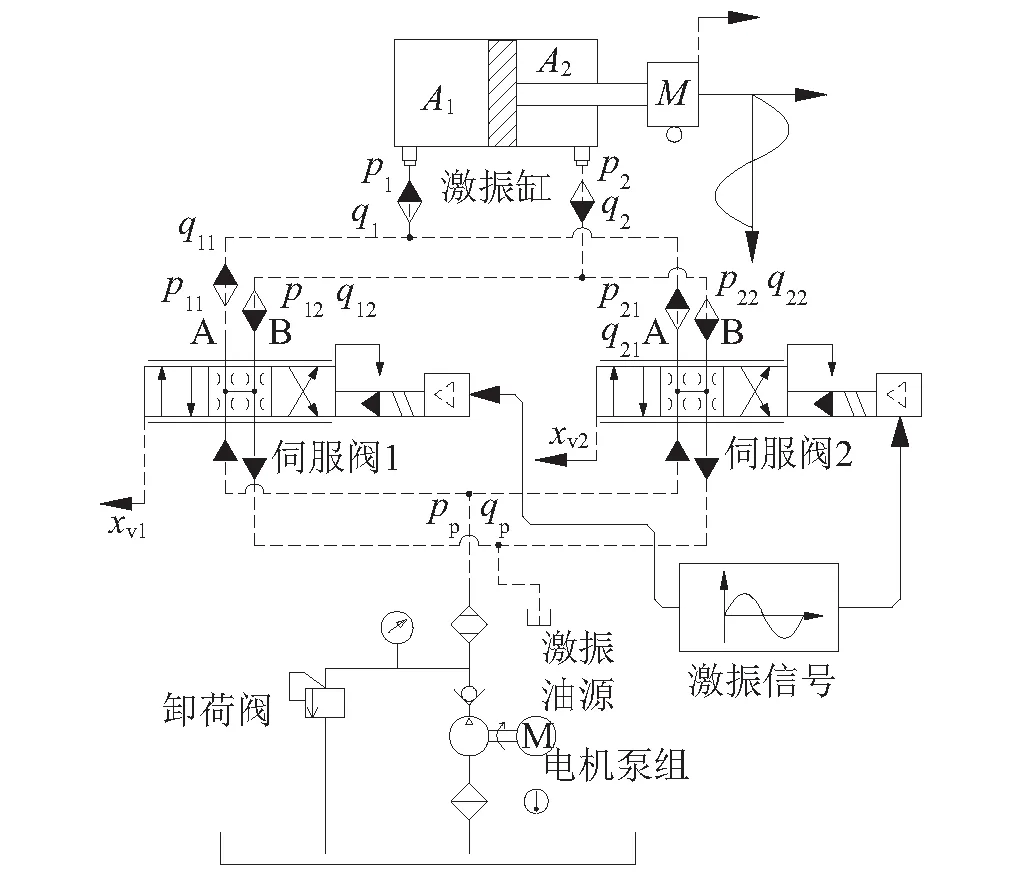
图2 电液激振系统简图Fig.2 Simplified diagram of electro-hydraulic excite system

2.1流体激振力模型

2.1.1 流量模型

如图2所示，为了提高伺服阀阀芯换向运动时的输出流量，激振系统采用了同样规格的双伺服阀并联方式。因此根据文献[14]所列的单阀模型，再引入伯努利定理[15]，则多通道阀口的耦合流量可表示为

(2)

(3)

式中：q1和q2为激振缸有杆腔和无杆腔的流量，mL/min；Cd为阀口流量系数，无量纲；w1和w2为阀口面积梯度，mm； 当采用对称阀时，w1=w2；xvi为第i个阀的阀芯位移，mm；p1和p2为激振缸有杆腔和无杆腔的压力，MPa；ρ为液压油密度，kg/m3。(i=1,2)

2.1.2 输出力模型

激振缸输出力Fp与两腔的压差直接相关，将式(1)，式(2)分别用Taylor级数展开并拉氏变换，再综合非对称激振缸两腔的流量连续性方程，可得激振系统输出力的复数域表达式为

(4)

式中：Kq是伺服阀的流量增益，Kq=∂q/∂xv，m2/s；Kp是伺服阀的流量压力系数，Kp=∂q/∂p，m3/(s·Pa)；βe为液压油的容积模数，MPa；A1和A2分别为激振缸有杆腔和无杆腔的面积，mm2。

2.2 拉削负载力模型

拉削刀具与普通切削刀具最大的区别在于，拉刀由齿升量替代了进刀量，因此拉削过程实质上是拉刀与工件相对直线运动的过程，如图3所示。

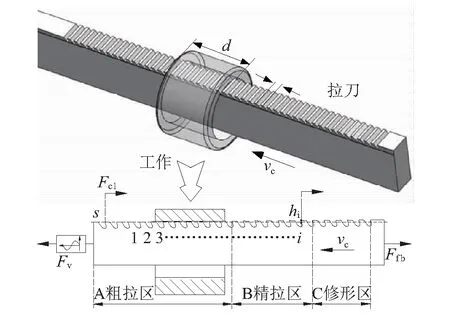
图3 拉削负载示意图Fig.3 Schematic diagram of broaching

拉削力Fc根据大量拉削工程数据可拟合表示为[16]

Fc=λzklilwi

(5)

式中：λ为与刀齿前角等因素有关的修正系数，其值可近似表示为cosα，α为刀齿前角；z为同时参与切削的刀齿个数；kli为刀齿单位切削刃长度上的拉削力，N/mm；lwi为刀齿切削刃长度，mm。

为简化分析，拉刀上刀齿前角α都相等；当深度切削时，参与切削的刀齿切削刃长度lw也相同；刀齿单位切削刃长度上的拉削力也可用经验公式表示

(6)

式中：σb为工件材料的屈服强度，MPa；hi为刀齿齿升量，可用平均齿升量计算，mm。

2.3 激振系统传递函数

由于伺服阀的频响快于系统中的其他元件，忽略其动态特性对系统的影响，将其视作惯性环节。因此，综合式(1)、式(4)、式(5)，可得激振系统的传递函数为

(7)

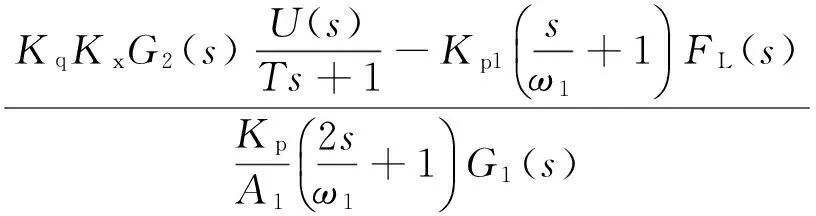
(8)

式中：Kx为阀芯位移综合增益系数，mm/V；U为控制电压，V；T为时间常数。

FL(s)=Fc(s)+Ff(s)，Kp1=(1-η)Kp，

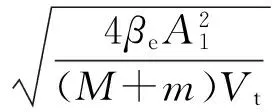
G2(s)=2G1(s)+A1(η-1)

2.4 系统响应函数

激振系统自身的稳定性可根据式(7)和(8)所示的传递函数，通过Bode图求解剪切频率进行判别。但激振系统在周期激励信号及外界负载作用下的稳定性，则只能通过其动态响应特性决定。

由式(7)和式(8)所示，其时域响应表达式为

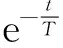
(9)

(10)

式中：

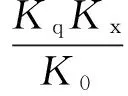
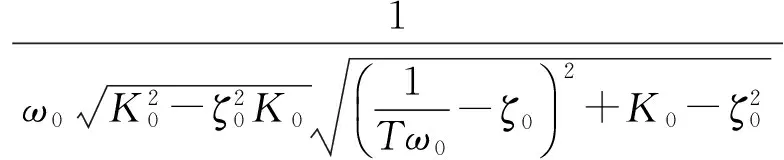
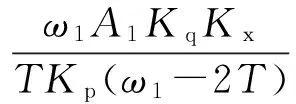
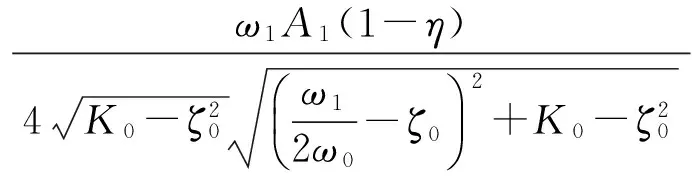
3 试验结果与讨论

本文分别通过MATLAB仿真计算和振动拉削平台实验，对比分析振动拉削激振系统输出波形的稳定性。其中仿真计算主要基于系统传递函数式(7)、式(8)和时域响应函数式(9)、式(10)，求解开环系统Bode曲线和在脉冲阶跃信号下的响应幅频曲线；而实测实验则以如图4所示的电液激振拉削实验平台为基础，基于三档激振频率(10 Hz，20 Hz和50 Hz)以及拉削负载自身的时变属性，从实测数据上分析系统输出幅值稳定特性。

实验系统所用激振阀为Rexroth伺服阀4WSE2EM6，在7 MPa压差下的额定流量为25 L/min，该型伺服阀集成了控制电气元件，供电电压为±15 V，控制信号为电压±10 V；控制器为SIMENS S7-300PLC，包含了IO模块及四通道DA模块，其中DA模块与伺服阀信号连接，采用定时中断的方式发送阀芯周期控制信号。激振缸工作压力数据通过2个PTH503压力传感器(量程为0～15 MPa，综合精度0.5% FS，输出信号4～20 mA，频率响应5 ms)从无杆腔和有杆腔采样获得；激振缸位移数据通过HLG103AC5激光位移传感器(量程±4 mm，分辨率0.5 μm，线性度±0.1% FS，输出信号4～20 mA) 从激振缸活塞杆获得。实验相关参数如表1和表2所示，实验结果如图5～图10所示，其中图6所示为振动拉削过程激振缸输出全程实测结果，系统激励信号为方波信号

(11)

如图6所示，拉削过程可区分为空载段(0-2 s)，拉削段(2-6 s)和过载段(6-8 s)。特别在过载段，由于拉削负载力突变，使活塞逐渐偏置一端，逐步抑制了激振性能。

图4 实验系统示意图Fig.4 Schematic diagram of experimental system表1 双阀激振系统主要参数表Tab.1 Main parameters of dual-valve excitation system

参数数值阀电压位移增益Kv/(mm·V-1)0.1阀流量增益Kq/(m2·s-1)0.083阀流量压力系数Kp/(m3·(s·Pa)-1)1.92×10-12阀口面积梯度w/mm5.65阀流量系数Cd0.6时间常数T/ms2系统压力pp/MPa7液压油密度ρ/(kg·m-3)900非对称比例系数η0.609液压油容积模数βe/MPa700黏性阻尼系数C/(N·s·m-1)300系统摩擦力Ff/N200激振缸行程Ls/mm10激振缸无杆腔面积A1/mm25026.54激振缸有杆腔面积A2/mm23063.05折算到活塞的总质量M/kg10拉刀规格/mm3600×16×40平均齿升量hi/mm0.04刀齿前角α0/(°)15刀齿间距p/mm6拉刀质量m/kg10加工键槽尺寸/mm339×16×1.7工件材料45钢

表2 刀齿拉削宽度参数表Tab.2 Parameters of broaching width of cutters

图5 传递函数Bode图Fig.5 Transfer function Bode diagram

图6 激振缸输出实测结果图(全程)Fig.6 Output of excitation cylinder(whole process)

3.1 激振系统自体稳定性

(12)

3.2 激振频率下的稳定性

图7所示为空载仿真响应曲线，系统激励信号模拟了振动拉削的三种主要工作频率，即周期Te分别为20 ms，50 ms和100 ms的单周期方波信号，

(13)

如图7所示，随着输入信号频率递增，系统响应幅值递减，与初始位置的偏移量也发生递减，幅值波动正反向的非对称性也发生了变化。因此为了获取较好的振动拉削效果，需平衡好激振频率与输出幅值的关系，此外提高激振频率，可使系统在正反向切换时响应更加平滑，使输出波形更容易稳定。

图8所示为空载段激振缸输出力和输出位移的实测结果。如图6和图8所示，与仿真结果类似，激振频率明显影响了系统输出幅值和振动平衡位置，在稳定阶段10 Hz时位移平均幅值为0.654 mm，平衡位置为0.208 mm，20 Hz时分别为0.312 mm和0.102 mm，50 Hz时分别为0.147 mm和0.013 mm。输出力曲线也出现了同样的趋势，其原因在于，激振缸的容腔压力变化相对输入流量是一惯性环节，因此随着激励信号频率提高，阀芯切换节奏相对加快，导致压力增量不足，系统输出幅值发生衰减。这一特性使得为了获取更好的输出波形，需提高激振系统的油源压力。

图7 基于输入频率的响应曲线Fig.7 Response curve based on input frequency

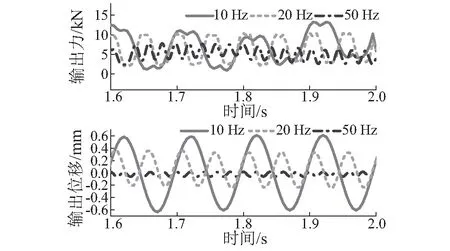
图8 激振缸输出实测结果图(空载段)Fig.8 Output of excitation cylinder (the range without load)

3.3 拉削负载下的稳定性

图9所示为系统模型在外部载荷扰动下的仿真响应曲线，其输入信号为在时刻t=0.1 s时，幅值从10变化为0的下降沿信号。如图所示，随着外部负载增大，输出响应幅值也增大，也会使波形振荡次数发生变化。而且当激励信号降为0时，系统输出波形会发生明显的偏移，载荷越大，偏移越明显。因此，为了获取较好的振动波形，需严谨核算拉削力幅值，并基于该幅值对激振缸平衡位置进行在线补偿。

根据式(6)所示的拉削力表达式及表2所示的拉削尺寸特征，可得出在振动拉削过程中，拉削负载力为递增值。因此，如图6和图10所示，随着拉削力增大，激振系统输出波形的“毛刺”也在增多，波形也越不稳定，当拉削负载力超过激振缸所能提供的最大驱动力后，激振缸出现了严重的偏移，此时激振系统内部虽仍有压力波动变化，但外部已无输出位移。其原因在于，拉削力作为外因，其阻碍了激振缸容腔体积的变化，降低了激振缸瞬时速度，使得有杆腔压力升高，降低了正向周期中两腔的压差，也使输出力和输出位移波形变得不稳定。因此，受文献[6-7,17]的启发，为了获取较好的振动波形，可在油路中增加蓄能装置，“过滤”压力“毛刺”，该处理措施主要增大了系统的阻尼，可吸收及补偿能量，减少振荡次数；或者通过增加大流量的直通开关阀，平衡激振缸两腔的压力配比，该措施主要是为了补偿激振缸两腔的流量，维持激振缸活塞的平衡位置。

图9 基于负载力的响应曲线Fig.9 Response curve based on broaching force

图10 激振缸输出实测结果图(拉削段)Fig.10 Output of excitation cylinder (broaching)

4 结 论

(1) 本文综合考虑了双阀激振系统的流量耦合线性模型和拉削负载力模型，推导了振动拉削电液激振系统的传递函数和时域响应函数，基于理论仿真计算和实际系统测试，研究了振动拉削过程中激振系统输出波形的稳定性。

(2) 仿真与试验结果表明，激振缸的缸径D与行程Ls的比值要越大越好，但增大极限响应频率ω0也会使幅频曲线上移，剪切频率ωc增大，影响了空载条件下的系统稳定性。而激励信号的频率会影响输出波形的平衡位置及波动幅值，激励信号频率越高，输出波形越容易调节；拉削负载力主要影响了输出波形的振荡次数，负载力越大，输出波形越不稳定。

(3) 为了有效改善拉削过程中激振输出幅值的不稳定性，可适当提高激励信号的频率，为了弥补由此带来的幅值衰减，需提高激振系统的油源压力。此外，为了获取较好的振动波形，可在油路中增加蓄能装置或者大流量的直通开关阀，平衡激振缸两腔的压力配比。

(4) 本文针对振动加工过程中激振输出波形稳定性问题，所提出的分析方法及解决方案可满足低频振动加工领域工程实际需要。

[1] 隈部淳一郎. 精密加工振动切削基础与应用[M]. 北京：机械工业出版社，1985.

[2] 余洋，石博强，侯友山. 结构刚度对液压伺服系统稳定性影响分析[J]. 农业工程学报，2011，27：32-35.

YU Yang, SHI Boqiang, HOU Youshan. Analysis on stability of hydraulic servo systems affected by structure stiffness[J]. Transactions of the CSAE，2011，27: 32-35.

[3] 姜万录，朱勇，郑直，等.电液伺服系统非线性振动机理及试验研究[J]. 机械工程学报，2015，51(4): 175-184.

JIANG Wanlu，ZHU Yong，ZHENG Zhi，et al. Nonlinear vibration mechanism of electro-hydraulic servo system and its experimental verification[J]. Journal of Mechanical Engineering，2015，51(4): 175-184.

[4] 葛振亮，侯友山，姜勇. 工程车辆全液压转向系统管路特性分析[J]. 振动与冲击，2011，30(3): 60-63.

GE Zhenliang, HOU Youshan, JIANG Yong. Dynamic characteristics analysis of hydraulic pipes in fully hydraulic steering system of engineering vehicles[J]. Journal of Vibration and Shock，2011，30(3): 60-63.

[5] 金智林，郭立书，施瑞康，等. 汽车电控液压制动系统动态性能分析及试验研究[J]. 机械工程学报，2012，48(12): 127-132.

JIN Zhilin, GUO Lishu, SHI Ruikang, et al. Experimental study on dynamic characteristics of electro hydraulic brake system for vehicle[J]. Journal of Mechanical Engineering，2012，48(12): 127-132.

[6] 滕韬，夏毅敏，杨务滋，等. 盾构刀盘驱动液压系统压力冲击吸收特性分析[J]. 浙江大学学报(工学版)，2011，45(5): 864-868.

TENG Tao, XIA Yimin, YANG Wuzi, et al. Characteristics analysis of pressure impact absorption for shield cutter head drive hydraulic system[J]. Journal of Zhejiang University(Engineering Science) ，2011，45(5): 864-868.

[7] 李锦，黄长征. 盾构机液压推进系统稳定性研究[J]. 液压与气动，2014(3): 54-57.

LI Jin, HUANG Changzheng. Study on stability of hydraulic propulsion system for shiled tunneling machine[J]. Chinese Hydraulics & Pneumatics，2014(3): 54-57.

[8] 王爱国. 全液压矫直机液压伺服非线性系统稳定性研究[J]. 太原科技大学学报，2014，35(6): 443-447.

WANG Aiguo. Research on the stability of nonlinear systems in hydraulic leveler of hydraulic servo system[J]. Journal of Taiyuan University of Science and Technology，2014，35(6): 443-447.

[9] AMIRANTE R，DISTASO E，TAMBURRANO P. Experimental and numerical analysis of cavitation in hydraulic proportional directional valves[J]. Energy Conversion and Management，2014，87: 208-219.

[10] YANG Z S，HE Z B，LI D W，et al. Hydraulic amplifier design and its application to direct drive valve based on magnetostrictive actuator[J]. Sensors and Actuators A:Physical，2014，216: 52-63.

[11] ZHAO J B，WANG J Z，WANG S K. Fractional order control to the electro-hydraulic system in insulator fatigue test device[J]. Mechatronics，2013，23: 828-839.

[12] SHEN G，ZHU Z C，ZHANG L，et al. Adaptive feed-forward compensation for hybrid control with acceleration time waveform replication on electro-hydraulic shaking table[J]. Control Engineering Practice，2013，21: 1128-1142.

[13] SIBIELAK M. Optimal controller for vibration isolation system with controlled hydraulic damper by piezoelectric stack[J]. Mechanical System and Signal Processing，2013，36: 118-126.

[14] 梅里特 H E. 液压控制系统[M]. 北京：科学出版社，1976.

[15] 罗惕乾. 流体力学[M]. 3版.北京：机械工业出版社，2014.

[16] 袁哲俊，刘华明. 金属切削刀具设计手册[M]. 北京：机械工业出版社，2008.

[17] 成大先. 机械设计手册：单行本，液压控制[M]. 5版.北京：化学工业出版社，2010.

Anexperimentandanalysisonoutputwaveformstabilityofadual-valveexcitationsystemduringvibrationbroaching

MENG Zhen1, NI Jing1, WU Chuanyu2

(1. School of Mechanical Engineering，Hangzhou Dianzi University，Hangzhou 310018，China；2. School of Mechanical Engineering and Automation，Zhejiang Sci-Tech University，Hangzhou 310018，China)

In order to investigate the output amplitude stability of an excitation system during vibration broaching, a transfer function of a dual-valve excitation system was established by considering the flow coupled linear model and the broaching force model. And the time domain response function of output force and displacement was obtained based on the transfer function. Then, the simulated results of aforementioned function were calculated by MATLAB, including Bode diagram and the response curve of time domain. Finally, the experimental data were compared with simulation results, which were obtained from the novel vibration broaching platform. The results show that the frequency of the excitation signal affects the balance position and the amplitude of the output waveform. The higher the frequency of the signal is, the easier the output waveform can be adjusted. The oscillation frequency of the output waveform is mainly affected by the broaching force. The greater the force was, the more unstable the output waveform was. Therefore, to make the output waveform more stable, the ratio of vibration cylinder bore and stroke should be improved, which can increase the response frequency. On the other hand, the energy storage device and flow type valve should be added, which can balance the pressure ratio of vibration cylinder cavity.

vibration broaching; electrical-hydraulic excitation; Bode diagram; waveform stability

国家自然科学基金资助项目(51375129)；浙江理工大学521人才培养计划资助

2016-05-10 修改稿收到日期： 2016-07-19

蒙臻 男，博士，1986年生

武传宇 男，博士，教授，博士生导师，1976年生

E-mail: cywu@zstu.edu.cn

TH137；TG57

A

10.13465/j.cnki.jvs.2017.20.014