含复杂结构应力的平板振动解析方法研究
2017-11-04陈炉云
杨 念, 陈炉云, 易 宏, 刘 勇
(1.上海交通大学 船建学院海洋工程重点实验室,上海 200240; 2.中船重工第七〇二研究所上海分部,上海 200011)
含复杂结构应力的平板振动解析方法研究
杨 念1, 陈炉云1, 易 宏1, 刘 勇2
(1.上海交通大学 船建学院海洋工程重点实验室,上海 200240; 2.中船重工第七〇二研究所上海分部,上海 200011)
工程结构物中常常含有分布形式复杂的非均匀结构应力,该应力会影响结构的振动特性。有限元法虽然可以求解,但不利于从本质上分析结构应力与振动的内在物理联系、不方便研究结构应力对振动的影响规律,而且还有施加特定非均布应力操作复杂、计算量较大等限制。在解析方法研究方面,以往的方法主要用来求解含整体均匀分布应力的结构,不适用于实际工程结构中的非均布应力的情况。提出了一种求解含非均布应力结构振动的解析方法,以平板结构为对象,用特殊级数形式表示非均布的结构应力,将应力影响加到原平板振动方程,并实现结构模态的部分解耦,然后对解耦后的方程进行求解得到解析解。推导出的解析方法适用于任意应力状态下的平板振动求解,并且相对于有限元法有计算量小、物理解释明晰等优点,方便定性地研究结构应力与振动之间的物理联系,进行考虑结构应力的振动精确预报与控制。
复杂应力;平板结构;振动;解析法
由于工程结构的复杂化及工作环境的特殊性,在承受工况载荷之前,结构中往往已经存在着一定的应力。这些应力中有些是人为施加的,如桥梁、土木结构中施加的预应力;有些是在实际加工过程中不可避免的,如焊接残余应力、结构制造缺陷、热效应等;有些是结构因外部工作环境而产生的,如潜艇壳中因外部水压力而产生的壳体应力、立管因复杂深海环境而产生的管体应力。这些应力的存在使得结构在承受工况载荷之前便已处在一个复杂的应力状态下,研究这类应力对结构特性特别是动力学特性的影响是结构设计中的一个重要内容。
在广义预应力结构的动力学特性研究方面,Doong[1]采用根据高阶剪切变形理论推导了含预应力矩形厚板的控制方程,并将计算结果与文献[2]进行了比较。高永毅等[3]对有、无焊接残余应力的平板的固有频率进行了对比实验。在含预应力壳体结构动力学研究方面,陈章兰等[4]运用有限元法计算了焊接热应力对船舶动力特性的影响。刘志忠等[5-6]研究了流体静压对圆柱壳频散特性和功率流的影响。Fuller等[7]建立了充液圆柱壳的自由振动方程,对频散特性及振动能量流的分布规律作了深入研究。Zhang等[8-9]利用波传播方法分析了水下圆柱壳结构和充液圆柱壳结构的自由振动特性。过去,在含应力的结构动力学研究领域主要关注的是应力呈整体均匀分布的情况,对于局部复杂应力问题(应力幅值随位置变化而变)的研究比较少,只有一些针对某种特定分布应力的研究,但其方法不适用于其他分布形式的应力。而实际工程结构中的应力往往呈局部非均匀分布,并且因具体工况的不同而不同。因此以往研究中的方法并不适用于此类问题。有限元方法虽然在一定程度上可以求解此类问题[10-11],但其不能从本质上分析结构应力与振动的内在物理联系,并且有限元法施加非均布应力的操作比较复杂,当应力变化时又需要重新施加应力,对于大型结构物的建模和计算的工作量非常大,不方便进行探索结构应力对振动的影响规律和特点等定性研究工作。
针对这种情况,本文提出一种适用于求解含非均布应力结构振动的解析方法。本文以平板结构为对象,用特殊级数形式表示非均布的结构应力,将应力影响加到原结构振动方程中,实现结构模态的部分解耦,然后对解耦后的方程进行求解得到解析解。本文推导的解析方法适用于任意应力状态下的平板振动求解,相对于传统方法适用范围更广,相对于有限元法有计算量小、物理解释明晰等优点,方便我们定性地研究结构应力与振动之间的内在联系、影响特点。
1 理论分析
含应力的结构在本质上属于广义预应力结构。但是以往预应力结构振动的研究对象一般是整体均匀分布应力[12]。因此,非均匀分布的结构应力对结构振动的影响需要进行重新推导。平板结构是工程结构中的常用结构形式,本文的推导以平板结构为对象。
1.1 基本方程


图1 平板模型Fig.1 Plate model
从平板中截取一个微元体,其长宽分别为dx和dy。微元体处于静止状态时,在结构应力的作用下其受力情况如图2所示。

图2 结构应力引起的截面力Fig.2 Section force caused by initial stress

(1)

(2)
同理可得其他的结构应力在z方向上的出现的新分量
(3)
基于Kirchhoff薄板理论,沿厚度方向应力不变,所以本文不考虑残余应力产生的新的耦合弯矩和扭矩。
在振动过程中结构应力与振动位移在z方向产生了新的耦合力,会对微元体的力平衡方程产生影响,从而改变了结构运动方程。将这些新的耦合力代入Kirchhoff平板运动方程可以得到复杂应力平板运动方程
(4)


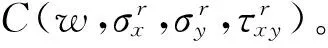
假设平板边界条件为四边简支,满足边界条件的位移可表示为
(5)
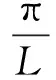
将式(5)代入式(4),且等号两边同时乘以sin (mαx)和sin (nβy),利用三角级数的正交性可以得到

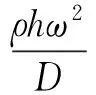
(6)
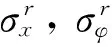
1.2 振动方程求解
(7)
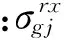
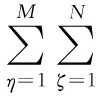
W(m+g)(n-j)[(m+g)α]2+W(m+g)(n+j)[(m+g)α]2}m>gandn>j(8a)
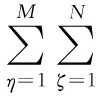
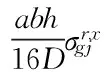
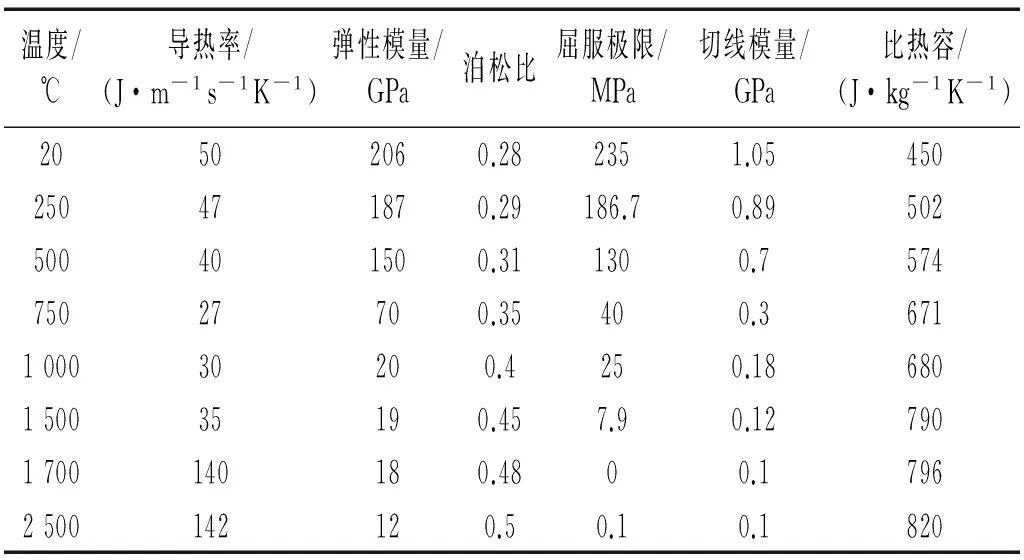
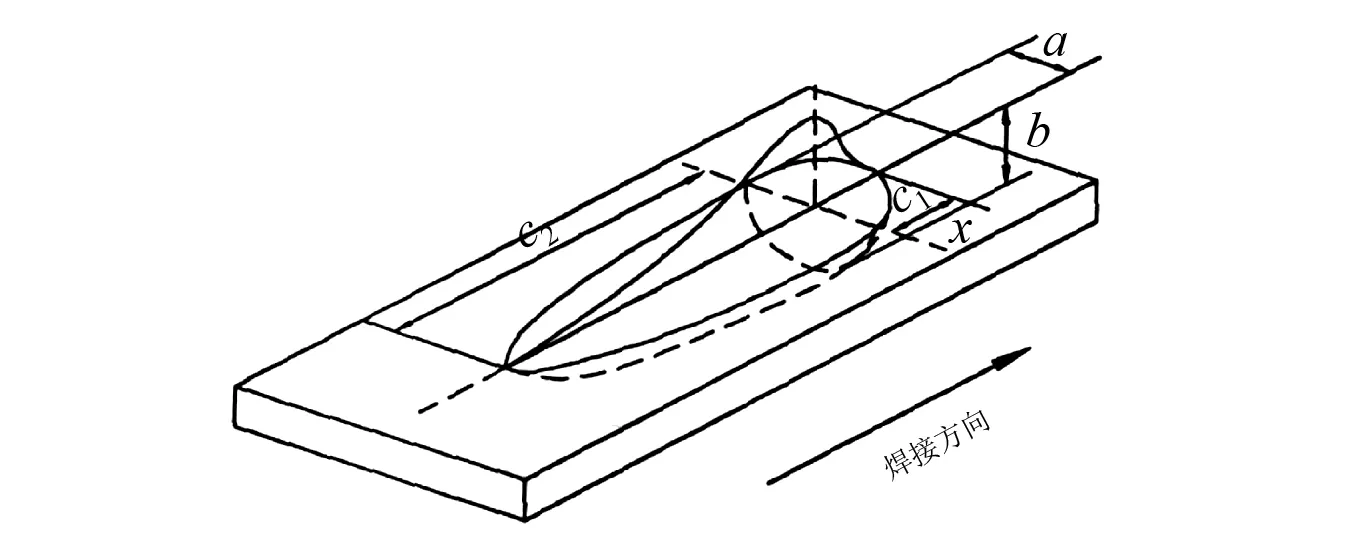
W(m+g)(n-j)[(m+g)α]2+W(m+g)(n+j)[(m+g)α]2}m>gandn W(m+g)(n-j)[(m+g)α]2+W(m+g)(n+j)[(m+g)α]2}m W(m+g)|n-j|[(m+g)α]2+W(m+g)(n+j)[(m+g)α]2}m 从式(8)可以看出,含应力结构的振动模态只和特定模态产生耦合,而不是和其他所有模态都有耦合。利用这一性质,可实现含应力结构运动方程的部分解耦,从而进行方程求解。再按相同方法对K的其他项进行化简,这样就可以建立M×N个方程,联立方程组并将其表示为矩阵形式 (Λ+Rgj)X=0 (9) (10) 按照相同的方法,可以建立M×N个方程并表示为矩阵形式 (Λ+R)X=0 (11) 此时应力影响矩阵R也相应的可表示为矩阵级数形式 (12) 大部分的分布函数都可以表示为三角级数形式,因此对于实际结构中分布形式复杂的应力,本文方法均可适用。 自由振动求解,令式(11)的系数矩阵行列式为零,即: |Λ+R|=0 (13) 求解式(13)就可以得到任意应力状态下的平板固有频率和振型。 若平板受垂向分布激励力fz,则含结构应力的平板强迫振动方程为 (14) 将fz表示成与位移相同的级数形式 (15) 将式(5)和式(15)代入式(14),再用相同的方法可建立含结构应力的平板强迫振动矩阵方程 (Λ+R)X=F (16) 求解式(16)即可得到位移展开系数Wmn,将其代入式(5),即可求得含结构应力平板的强迫振动响应。 2.1 正弦应力算例 图3 结构应力分布图Fig.3 Structural stress distribution 2.2 实际复杂应力算例 本节运用本文解析方法和有限元方法计算含有焊接残余应力平板的固有频率。平板的几何参数为长2 m,宽2 m,厚度0.02 m。假设在x=1 m处有一条对接焊缝,如图4所示。 目前热弹塑性有限元方法被广泛的应用于焊接过程模拟和焊接残余应力的计算[14],因此本文采用商用有限元软件Marc计算焊接残余应力。焊接材料为Q235低碳钢,其热物理参数如表2所示,考虑了钢材热物理参数和力学参数随温度变化的非线性,并将相变潜热换成等效比热容来考虑相变的影响[15],焊接材料的塑性强化模式选用双线性等向强化模式。 表1 解析方法和有限元方法计算结果比较Tab.1 The result comparison form analyticalmethod and finite element method 图4 焊缝位置Fig.4 Weld location表2 焊接材料热物理参数[16]Tab.2 The thermo-physical parameters of welding material 温度/℃导热率/(J·m-1s-1K-1)弹性模量/GPa泊松比屈服极限/MPa切线模量/GPa比热容/(J·kg-1K-1)20502060.282351.05450250471870.29186.70.89502500401500.311300.757475027700.35400.3671100030200.4250.18680150035190.457.90.127901700140180.4800.17962500142120.50.10.1820 热源采用Goldak提出的双椭球热源模型(如图5所示), 此模型设定体热源的前半部为1/4椭球, 后半部分为另一个1/4椭球。椭球热源参数值a=4 mm,b=3 mm,c1=2 mm,c2=8 mm。 图5 双椭球热源模型Fig.5 Double ellipsoid heat source model 焊接采用手弧电弧焊,电流为180 A,电压为30 V,焊接速度为5 mm/s。根据热弹塑性有限元方法的计算结果,将纵向残余应力和横向残余应力拟合三角级数的形式,如图6所示。 (a)y=1截面纵向残余应力 (b)x=1截面横向残余应力图6 平板焊接残余应力Fig.6 Plate welding residual stress 分别使用本文解析方法和有限元方法计算该板的固有频率,前十阶固有频率如表3所示。 表3 解析方法和有限元方法计算结果Tab.3 The result form analytical methodand finite element method 由上面两个算例可以看出,本文提出的解析方法计算结果与有限元方法计算结果基本吻合,验证了本章方法的正确性。在以往的研究中,人们比较重视结构应力对结构极限强度的影响,通过算例可以发现复杂结构应力对平板结构的固有频率的影响也是不容忽视的。 此外,有限元方法解决此类问题的操作过程较复杂。如果对于大型结构,有限元方法的自由度和计算量将变得十分巨大,应力施加操作也会更加复杂。所以相对于有限元方法,本文的解析方法在定性研究结构应力与振动之间的内在物理关系和影响特点时是具有优势的。 本文以平板结构为对象,从基本力学理论分析入手,将结构应力表示成特殊级数形式加入振动方程中,实现部分解耦,推导了含非均布应力的结构振动方程,并求得解析解。本文推导的解析方法可以用于任意应力状态下的平板振动求解,相对于传统方法适用范围更广,相对于有限元法有计算量小、物理解释明晰等优点,方便我们研究结构应力与振动之间的内在联系与影响特点,进行考虑结构应力的振动精确预报与控制。在数值算例中,分别运用本文方法和有限元方法对不同分布类型的结构应力的影响情况进行了计算,计算结果基本吻合,验证了本章方法的正确性。 [1] DOONG J L. Vibration and stability of an initially stressed thick plate according to a high-order deformation theory[J]. Journal of Sound and Vibration, 1987, 113(3): 425-440. [2] BRUNELLE E J, ROBERTSON S R. Vibrations of an initially stressed thick plate[J]. Journal of Sound and Vibration, 1976, 45(3): 405-416. [3] 高永毅,刘德顺. 利用试验模态分析进行残余应力评估的研究[J]. 振动与冲击, 2005, 24(5): 111-114. GAO Yongyi, LIU Deshun. Studies on estimation of residual stress using modal analysis[J]. Journal of Vibration and Shock, 2005, 24(5): 111-114. [4] 陈章兰,叶家玮. 焊接热效应对船舶动力学性能影响的有限元分析[J]. 大连海事大学学报, 2013, 39(2): 53-56. CHEN Zhanglan, YE Jiawei. Influence analysis of welding thermal effect on hull dynamic performance[J]. Journal of Dalian Maritime University, 2013, 39(2): 53-56. [5] 刘志忠,李天匀,张俊杰. 考虑流体静压时充液圆柱壳的输入能量流特性[J]. 中国舰船研究, 2009, 4(2): 20-23. LIU Zhizhong, LI Tianyun, ZHANG Junjie. Input vibration power flow in fluid-filled cylindrical shells considering hydrostatic pressure[J]. Chinese Journal of Ship Research, 2009, 4(2): 20-23. [6] LIU Z, LI T, ZHU X, et al. The effect of hydrostatic pressure fields on the dispersion characteristics of fluid-shell coupled system[J]. Journal of Marine Science and Application, 2010, 9(2): 129-136. [7] FULLER C R. The effects of wall diseontinuities on the propagation of flexural waves in cylindrieal shells[J]. Joumal of Sound and Vibration, 1981, 75(2): 207-228. [8] ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration, 2001, 239(3): 397-403. [9] ZHANG X M, LIU G R, LAM K Y. Frequency analysis of cylindrical panels using a wave propagation approach[J]. Applied Acoustics, 2001, 62(5): 527-543. [10] 陈炉云, 李磊鑫, 张裕芳. 含局部预应力的圆柱壳结构声辐射特性分析[J]. 上海交通大学学报, 2014, 48(8): 78-64. CHEN Luyun, LI Leixin, ZHANG Yufang. Characteristics anylysis of structural-acoustic of cylinder shell with prestress in local areas[J]. Journal of Shanghai Jiaotong University, 2014, 48(8) : 78-64. [11] 熊健民,周俊荣,周金枝. 基于 ANSYS 预应力简支梁固有频率的研究[J]. 固体力学学报, 2008, 29: 158-161. XIONG Jianmin, ZHOU Junrong, ZHOU Jinzhi. Research of pre-stress simple-supported beam’s natural frequency based on ansys[J]. Chinese Journal of Solid Mechanics, 2008, 29: 158-161. [12] 朱大同. 充液圆柱壳的自振特性[J]. 力学学报, 1984, 16(2): 141-150. ZHU Datong. On the free vibration of a circular cylindrical shell filled with liquied[J]. Theo & Appl Mech Letters, 1984, 16(2): 141-150. [13] 曹志远. 板壳振动理论[M]. 北京: 中国铁道出版社, 1989. [14] BARSOUM Z, LUNDBCK A. Simplified FE welding simulation of fillet welds-3D effects on the formation residual stresses[J]. Engineering Failure Analysis, 2009, 16: 2281-2289. [15] 赵明, 武传松, 陈茂爱. 焊接热过程数值分析中相变潜热的三种解决方案[J] . 焊接学报, 2006 (9): 55-58. ZHAO Ming, WU Chuansong, CHEN Mao’ai. Solution for latent heat of phase change in numerical analysis of arc welding[J]. Transactions of the China welding institution, 2006 (9): 55-58. [16] 马庆芳. 实用热物理性质手册[M]. 北京: 中国农业机械出版社, 1986. 附录A (A-1) (A-2) (A-3) (A-4) 附录B 当P=(m-1)×N+n,q=(|m-g|-1)×N+|n-j|时, 当p=(m-1)×N+n,q=(|m-g|-1)×N+n+j时 当p=(m-1)×N+n,q=(m+g-1)×N+|n-j|时, 当p=(m-1)×N+n,q=(m+g-1)×N+n+j时, Ananalyticalstudyofcomplexstressedplatevibration YANG Nian1, CHEN Luyun1, YI Hong1, LIU Yong2 (1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;2. Ship Scientific Research Center of China, Shanghai Branch, Shanghai 200011, China) There often exists non-uniform distributed stress in practical engineering structures, and this kind of stress affects structural vibration. Although finite element method (FEM) can solve this problem, it cannot help us with understanding the physical mechanism between structural stress and vibration. At the same time, FEM has other shortages like the process of applying non-uniform stress is complicated and calculation cost is huge. For analytical methods, the traditional methods cannot be applied to deal with practical stress because they mainly focus on uniform distributed stress. In this paper, we come up with a novel analytical method, and represent the non-uniform stress with a special series form to obtain the partial decoupling. Then we solve this de-coupling vibration equation and get the analytical solution. The method can be applied to solve the vibration of plate structures with arbitrary stress state and has the advantages to FEM in calculation cost and physical explanation. It can help us with understanding the connection between the structural stress and vibration and assists predicting and controlling the vibration. complex stress; plate structure; vibration; analytical method 海洋工程国家重点实验室基金资助(1507) 2016-01-18 修改稿收到日期: 2016-05-27 杨念 男,博士生,1989年生 易宏 男,教授,博士生导师,1962年生 TB535 A 10.13465/j.cnki.jvs.2017.20.003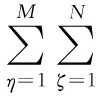
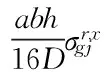
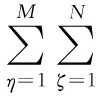
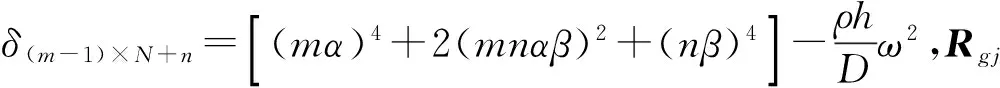


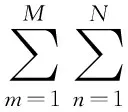
2 算例验证






3 结 论