新型磁浮车动力学仿真分析

汪科任， 罗世辉， 宗凌潇， 马卫华

(1. 西南交通大学 牵引动力国家重点实验室，成都 610031； 2.中铁十一局集团有限公司，武汉 430061)

新型磁浮车动力学仿真分析

汪科任1， 罗世辉1， 宗凌潇2， 马卫华1

(1. 西南交通大学 牵引动力国家重点实验室，成都 610031； 2.中铁十一局集团有限公司，武汉 430061)

为探究新型磁浮列车的动力学特性，利用SIMPACK软件建立了其56自由度的中低速磁浮车辆模型并进行相关仿真分析，并采用单悬浮架模型进行了乘坐舒适性试验验证。仿真结果表明：新型磁浮列车能够实现140 km/h在直线段稳定运行，车体横向加速度小于0.2 m/s2，车体垂向加速度小于0.5 m/s2，空载情况下能够实现30 km/h通过半径为50 m的弯道，车辆最大侧滚角不足0.04 rad，车体最大横向加速度小于1 m/s2，车体垂向加速度小于0.1 m/s2，悬浮间隙动态变化量最大仅为0.5 mm。 试验结果表明：以140 km/h的速度运行，与乘坐舒适性密切相关的车体垂向加速度约为0.5 m/s2。

新型磁悬浮列车；走行机构；弹簧中置；SIMPACK软件

磁浮列车因乘坐舒适、环境友好以及技术成熟等优点而具有较好的应用前景，其中主要以德国的高速TR系列与日本的中低速HSST系列为代表[1-2]。以HSST型为代表的中低速磁浮列车运用最为广泛，如韩国仁川机场磁浮线、中国长沙磁浮线等。国内外学者亦对磁浮列车的动力学特性进行了大量相关研究，文献[3]给出了利用SIMPACK建立多体动力学模型的方法，并用试验验证了该建模方法的可行性。文献[4]建立了76自由度中低速磁浮车辆动力学模型，优化了车辆导向机构相关参数。文献[5]建立了中低速磁浮动力学模型，并分析了悬浮控制系统、弹性桥梁的动态特性。文献[6-7]研究了磁浮列车以不同速度通过桥梁时的动力学特性。然而以上磁浮车动力学模型均采用传统的走行机构，如日本HSST型磁浮列车走行机构。以该走行机构为基础设计的悬浮列车一般最大运行速度仅为100 km/h，其与传统的地铁、轻轨运行速度相当。同时传统系列的走行结构通常较为复杂，设有迫导向机构，其可能不利于轻量化设计。加之减振空簧通常布置在悬浮架四端，不利于悬浮架之间的解耦等。针对以上问题本文设计了一种新型磁悬浮走行机构，该结构不仅能以更高的速度稳定运行，同时具有相对较轻的质量，满足在满载工况下通过半径为50 m的弯道，可在一定程度提高中低度磁浮列车的市场竞争力。以下是对该走行机构的具体说明。

1 新型磁浮系统走行机构设计方案

为简化走行机构，新型磁浮列车单节车采用3悬浮模块的结构[8]，新型转向架与传统的转向架不同之处：每个悬浮模块取消了迫导向机构；采用单抗侧滚梁结构设计；车体与悬架之间的减震空簧采用中置的方式；每节车中间悬浮模块中间滑台与车体铰接采用线性轴承结构形式，其余悬浮模块滑台与车体铰接采用固接式。同时以功率更高的长直线电机取代传统的短直线电机，提高了电机的牵引特性。以下为对各模块的简要说明。

1.1 单抗侧滚梁设计

顾名思义，抗侧滚梁主要作用为防止悬浮架在过弯时发生侧滚，能够实现较大线路的扭曲。传统型磁浮采用呈”口”字形结构的前后端部双抗侧滚梁，而新型磁浮采用“工”字形单抗侧滚梁中置的结构。其主要作用与传统的抗侧滚梁相似，如HSST型系列中低速磁浮列车。不同之处在于不仅结构更为简单，而且能够适应更大的曲线变化。

1.2 悬浮架解耦与线性轴承设计

传统的悬浮架结构采用互相耦合的5模块长编组走行机构，见图1。当其过弯道时，模块1、5支承车体的滑台相对车体的横移量最大，其次是模块2、4的滑台。由于空气弹簧本身倒置，其复位能力较弱，所以其必将导致在过小曲线时采用迫导向机构才能顺利过弯道。同时各模块之间通过滑块连接，该连接方式不仅不利于悬浮架之间的解耦，而且一旦其中一个模块运动不正常将直接影响其它模块的运动，最终的结果是严重影响悬浮列车的曲线通过能力，传统型磁浮列车过曲线见图2。而新型磁浮系统采用互相解耦的3模块编组走行机构，各悬浮架之间相互独立，见图3。同时中间滑台与车体的连接采用线性轴承，该连接方式可以释放滑台与车体之间的横向自由度。当列车过曲线时，与车体之间产生较大横移量的仅为中间悬浮架的空气弹簧，同时由于滑台1、3与车体之间采用固结的连接方式，不仅在过曲线时其连接点G基本保持在线路中心线上(见图4)，系统具有更强的曲线通过能力。而且由于采用了大空气弹簧正置的方式，当车辆过曲线时可利用空气弹簧的刚度产生恢复力，所以可取消机械辅助导向装置，简化了机构。

1.3 单铁控制器设计

带控制器的磁浮模型是模拟磁浮列车动力学行为最为理想的模型[9]，然而早期的磁浮车辆动力学研究中通常将电磁悬浮力等效为弹簧阻尼力，如文献[10-11]，但忽略悬浮控制器对电磁力主动调节作用的磁浮系统在悬浮稳定性、动态响应特性等方面与实际系系统存在较大差异[12]。考虑到悬浮系统的非线性特性，所以本文建立了磁浮列车单铁非线性PID控制器

图1 传统型走行机构Fig.1 Traditional series running mechanism

图2 传统型悬浮架过曲线Fig.2 Passing the curve of traditional running mechanism

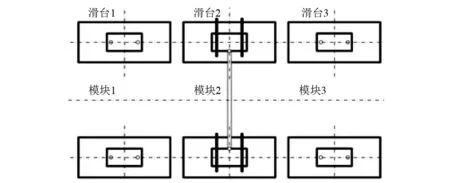
图3 新型走行机构Fig.3 New type of running mechanism

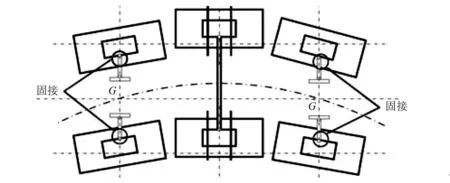
图4 新型悬浮架过曲线Fig.4 Passing the curve of new type of suspension frame

(1)

(2)

(3)

式中：R为电磁铁电阻，L为平衡位置处电感，Ps，Pi为平衡位置处间隙系数和电流系数，ΔU为电磁铁平衡位置处电压的变化量，μ为真空磁导率，A为悬浮电磁铁极面积，N为悬浮电磁铁线圈匝数，IN、CN分别为平衡位置处悬浮电流与悬浮气隙。在任意瞬时悬浮电磁铁吸引力F为

(4)

在弯道时的横向分力Fy与纵向分力Fz依据二维电磁力解析式[14]计算

(5)

(6)

式(4)中I为控制器瞬时电流，有I=IN+ΔI；式(5)中y为电磁铁与导轨之间的横向位移，W为磁极宽度。

图5 观测器结构Fig.5 Observer structure

2 动力学模型

2.1 车辆结构

在实际建模中需要对车辆结构进行合理的简化和等效。新型磁浮单节车共有56个自由度，无特殊说明外各转向架之间的运动学关系可参照文献[4]。整车动力学模型见图6。动力学模型部分参数见表1。

2.2 轨道不平顺模型

磁浮线路几何不平顺是激励车辆和轨道振动的主要外界干扰,所以合理的选取线路的轨道谱是必要的。

图6 整车动力学模型 Fig.6 The vehicle dynamic model表1 整车模型部分参数Tab.1 Part model parameters of the vehicle

序号名称端车/中间车1车体基本长度/mm9500/90002车辆基本长度/mm9850/97003车体基本宽度/mm28004车辆最大高度/mm≤35005车体自重/t16.36载重/t≤7.547悬浮模块长度/mm28808单悬浮架自重/t2.49空气弹簧垂向刚度/(kN·m-1)25010空气弹簧横向刚度/(kN·m-1)350

(7)

式中：f为空间频率，m-1,A，B，C，D，E，F，G为轨道谱特征参数。在中低速磁浮示范线中，唐山中低速磁浮示范线具有较好的代表意义，所以这里参照式(7)并通过反演计算可得唐山磁浮线水平与垂向不平顺分别如图7和8所示。

图7 轨道水平不平顺谱Fig.7 The horizontal irregularity spectrum of the track

图8 轨道垂向不平顺谱Fig.8 The vertical irregularity spectrum of the track

3 新型磁浮列车数值仿真

为实现新型中低速磁浮列车早期的方案验证，探讨其在直线段与曲线段的动力学特性，从一定程度上验证其是否满足设计要求。借助动力学仿真软件SIMPACK进行了相关动力学仿真，假设新型磁浮列车在混凝土复合梁上运行，这里将轨道作为刚性体处理，将轨道垂向不平顺与水平不平顺作为额定的外界激扰处理，采用图7与图8所示的不平顺轨道谱。

3.1 直线段动力学特性仿真分析

假设悬浮列车起浮位置为轨道梁下端16 mm，系统平衡位置悬浮气隙为8 mm。以整车的第二节单车为研究对象得出在140 km/h、空载工况下，新型磁悬浮列车悬浮间隙、车体横向加速度、垂向加速度动态响应分别如图9、10、11所示。由于悬浮模块是左右对称的，所以下面的所有仿真在无特殊说明的情况下仅以悬浮模块右侧的装配来说明。

图9 悬浮间隙Fig.9 Levitation gap

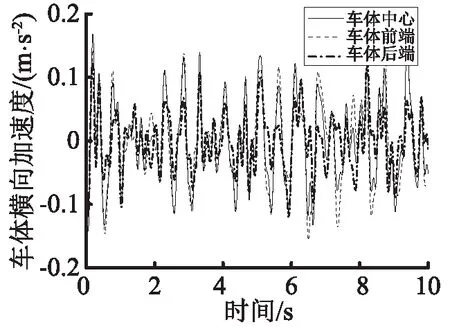
图10 车体横向加速度Fig.10 Lateral acceleration of car body

图11 车体垂向加速度Fig.11 Vertical acceleration of car body

通过对图9的分析可知，系统大约2 s左右便能达到稳定悬浮，超调量低于20%，考虑到仿真过程包括了系统的起浮动阶段，所以可知系统具有较好的动态响应特性。由图10分析可知，车体中心、车体前端、车体后端横向加速度均小于0.2 m/s2，满足横向加速度小于1 m/s2的要求[17]。对图11分析可知，车体中心、车体前端、车体后端垂向加速度在系统稳定后均低于0.5 m/s2，满足垂向加速度向上附加速度小于0.5 m/s2，向下附加速度小于1 m/s2的要求[17]，当系统稳定后车体质心垂向加速度仅为0.2 m/s2，符合UTACV走行品质规范—车体质心垂向加速度低于0.05g的要求[10]。进一步的对车辆运行平稳性指标分析可知，车辆横向平稳性指标W为1.59；车辆垂向平稳性指标W为1.61，参照表2所示的我国铁道动力学GB 5599—1985平稳性评定等级标准，可知车辆横向、垂向平稳性均达到了优秀的等级。

综上可知，新型磁悬浮列车能够实现在直线段以140 km/h的稳定运行，且具有较好的悬浮稳定性与较好的乘坐舒适性。

3.2 曲线段动力学特性仿真分析

由于直线段新型磁浮列车相关动力学特性3.1节已经进行了相关仿真分析，为更好的观察车辆在弯道的通过特性，仅在弯道段加入图7、8所示的轨道不平顺。仿真条件：轨道全长290 m，其中曲线段入口处直线轨道线路长为40 m，缓和曲线线路长为60 m，弯道半径为50 m，弯道线路长为100 m，弯道出口处缓和曲线长为60 m，直线段长为40 m，车速30 km/h，空载。

表2 车辆平稳性指标评定等级Tab.2 The vehicle stability index ranking

1)通过自主设计并加工的保温容器作为液氮冷浸装置，对不同含水饱和度的焦煤进行冷浸处理，煤样处理前后的渗透率试验结果表明，经液氮处理后的煤样渗透率增加幅度随含水饱和度增加成指数型增长，增加幅度为70.6%～1 254.9%。

单车仿真示意图见图12，新型磁悬浮列车中间模块悬浮间隙动态响应特性见图13。

图13中，下端横坐标为悬浮列车运行里程，上端横坐标为对应的仿真时间。对图13分析可知，系统在整个线路运动中，悬浮间隙相对平衡位置最大位移偏移量仅为0.5 mm，在半径为50 m的弯道具有较好的悬浮稳定性。进一步分析，由于系统是往右进入缓和曲线见图12，所以此时悬浮架往右侧有一定的倾斜，左侧(外侧)悬浮架的悬浮间隙在进入缓和曲线线路段时悬浮气隙由8 mm减小到7.5 mm，当进入半径为50 m弯道时，悬浮间隙偏移量达到最大值0.5 mm，并在弯道路段保持不变；当列车驶出弯道进入缓和曲线路段时，左侧悬浮架悬浮气隙由7.5 mm增加到8 mm，当驶出缓和曲线路段进入直线路段时维持在平衡悬浮间隙8 mm保持不变。右侧(内侧)悬浮架道理与右侧悬浮架相同，只是悬浮间隙的变化是相反的，这里不在赘述。

图12 仿真示意图Fig.12 The simulation diagram

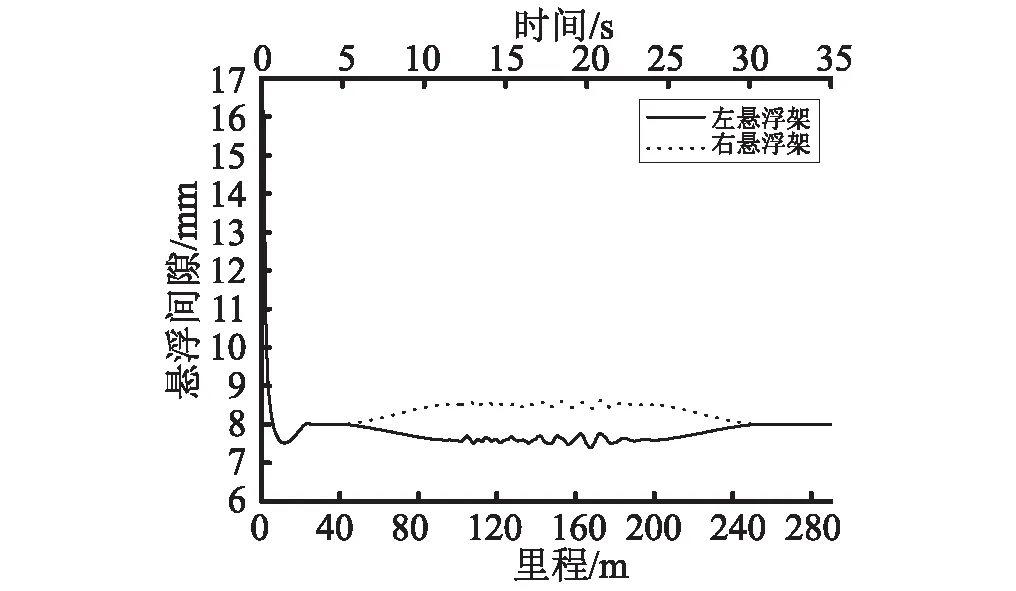
图13 悬浮间隙Fig.13 Levitation clearance

究其原因：当进入缓和曲线与弯道时由于悬浮架侧滚是不可避免的，所以整个悬浮架会略微侧滚，导致右侧悬浮架位移略微向下移动，而左侧悬浮架略微向上移动，所以出现了左悬浮架相对平衡位置略微上移，右侧悬浮架相对平衡位置略微下移的现象。

车辆过曲线段侧滚角动态特性见图14。

图14 车体侧滚角Fig.14 Carbody roll angle

由图14可知，车辆在通过半径为50 m弯道时最大侧滚角不到0.04 rad即2.29°，可知侧滚角较小，单侧抗侧滚梁具有较好的抗侧滚特性。

车辆过弯道车体横向加速度与垂向加速度分别如图15和16所示。

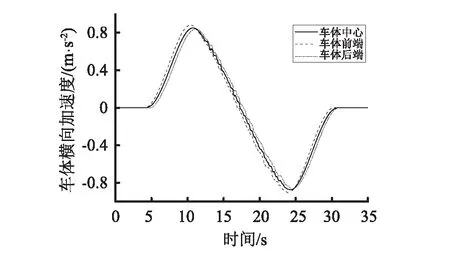
图15 车体横向加速度Fig.15 Carbody lateral acceleration

图16 车体垂向加速度Fig.16 Carbody vertical acceleration

图15分析可知，当车辆在整个290 m长线路运行过程中，车体横向加速度最大值出现在列车刚驶入与驶出弯道半径为50 m的曲线段时，最大横向加速度绝对值约低于1 m/s2，符合车体横向加速度最大值低于1 m/s2的要求。

图16分析可知，在半径为50 m的弯道上，车体垂向加速度约为0.2 m/s2，远低于0.5 m/s2，符合顾客乘坐舒适性标准。进一步的对车辆运行平稳性指标分析可知，车辆横向平稳性指标W为1.06；车辆垂向平稳性指标W为1.22，参照表2所示的铁道动力学GB 5599—1985平稳性评定等级标准，可知车辆横向、垂向平稳性均达到了优秀的等级。

相对于传统型中低速磁悬浮列车，新型中低速磁悬浮列车在导向机构与空簧的设计上有很大的不同，所以以下对空簧与中间滑台在列车过弯道时的相关动力学特性进行了相关仿真。图17为模块1、2、3中空簧横向作用力动态特性，图18为中间滑台相对车体的横向位移。

图17 空气弹簧横向力Fig.17 Air spring lateral force

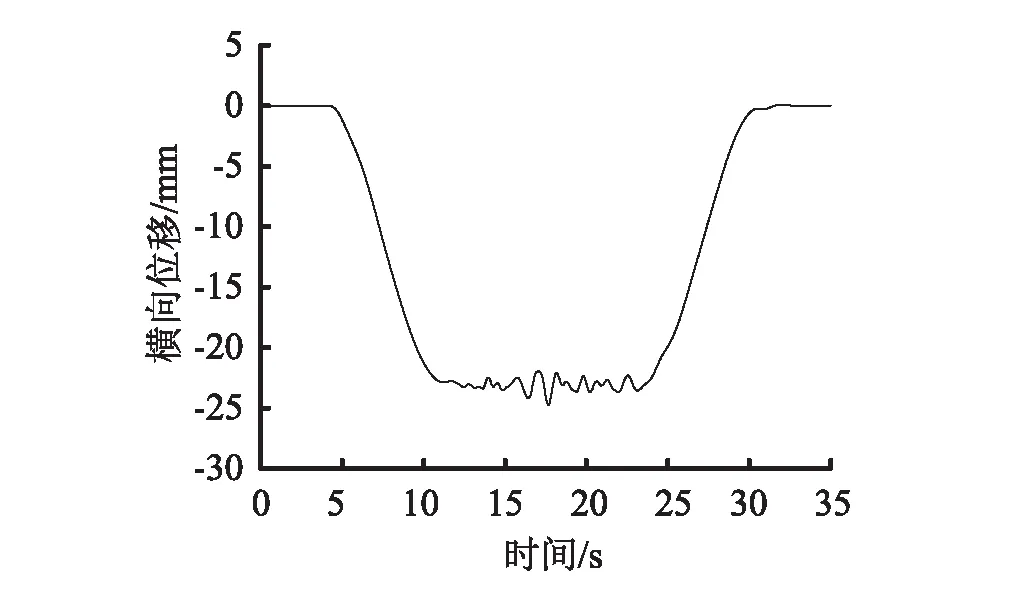
图18 相对横向位移Fig.18 The relative lateral displacement

由图17分析可知，模块1、3中右侧空簧横向力最大值均约为9 000 N，是由于模块1、3中滑台与车体之间采用固结的铰接方式，所以在过弯道时空簧可为车体提供较大的横向力来满足过弯道的要求。模块2中滑块与车体采用线性轴承的铰接方式，车体相对滑台具有较大范围的横向移动，所以模块2中空簧横向力较小，约为400 N。进一步分析可知，在图17曲线上升阶段，同一时刻模块3中空簧横向力均大于模块1中的空簧横向力，是由与此时列车正处于缓和曲线段上，当列车从直线段进入缓和曲线后，随着列车的运行，缓和曲线的曲率是增大的，而模块3总是处于曲率更大的曲线段上，所以其需要更大的向心加速度才能维持列车的稳定运行，从而需要空簧提供更大的横向力。在图17曲线下降阶段道理与上升阶段类似，随着列车从半径为50 m的圆曲线进入缓和曲线段后，随着列车的运行，曲率是减小的，所以同一时刻模块1中的空簧横向力是大于模块3的。而当列车在半径为50 m的圆曲线段运行的过程中，由于模块1与模块3所处曲线曲率相等，所以模块1与模块3中的空簧横向力大小是相等的，均为9 000 N。同时可以发现，模块1中空簧横向力曲线相对模块3的空弹簧横向力曲线具有一段时间的滞后，恰好反映了模块3中的空簧与模块1中空簧的纵向间距。

从图18可以看出此时中间滑台相对车体横向位移仅为23 mm，在可接受的范围内。

综上可知，在空载情况下新型磁悬浮列车能够以30 km/h稳定通过半径为50 m的弯道，平衡悬浮间隙变化量最大仅为0.5 mm，具有较好的乘坐舒适性与动力学特性。

4 试验验证

本节采用1：1单悬浮架模型进行试验验证。试验对象如图19所示。以特定的轨道不平顺外界激励来模拟时速140 km/h的运行情况，并对与乘坐舒适性相关的加速度进行了相关试验验证。

图19 试验现场Fig.19 Test site

其中测点1：托臂1；测点2：托臂2；测点3：F轨1；测点4：二级平台；测点5：悬浮车体平台，得出悬浮车体振动加速度、托臂1振动加速度分别如图20和21所示。

图20 悬浮车体振动加速度Fig.20 The acceleration of suspended carbody

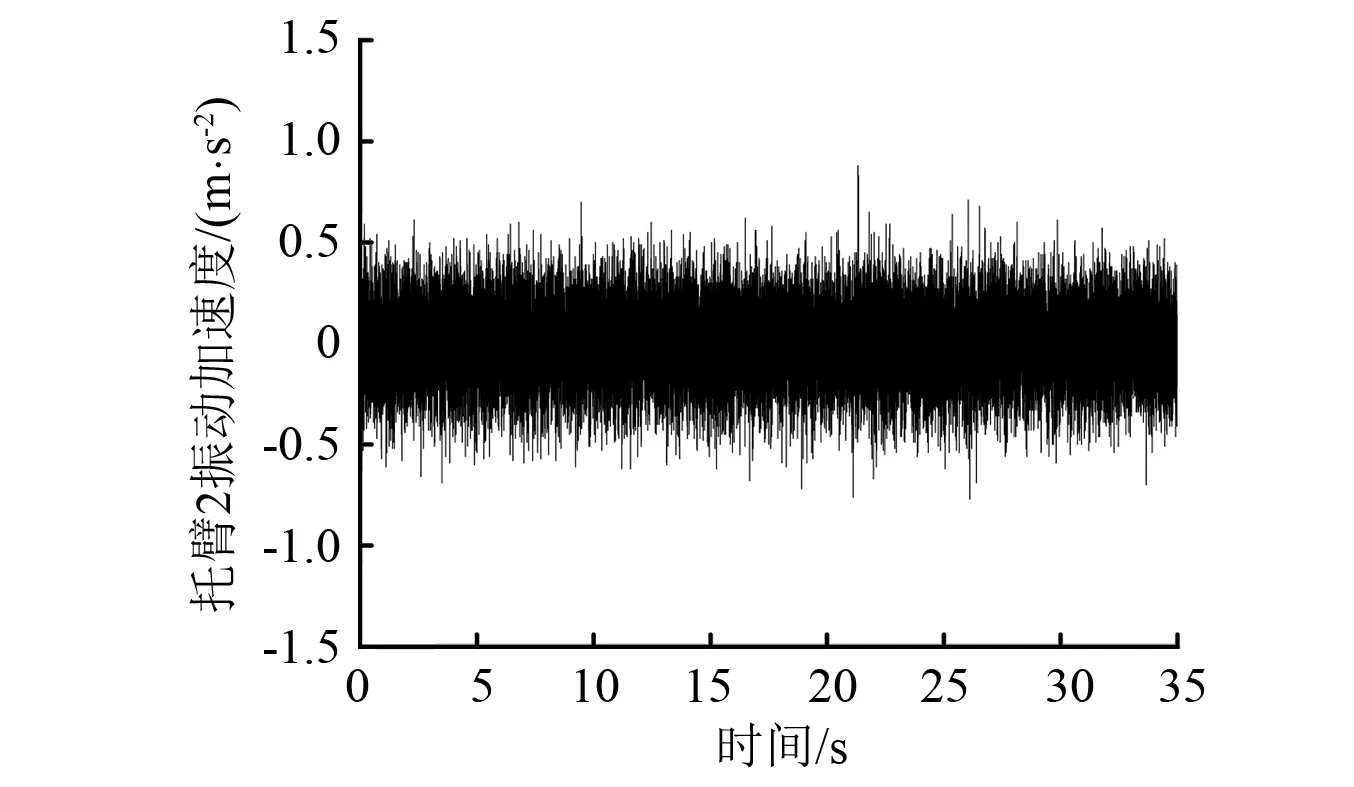
图21 托臂2振动加速度Fig.21 The acceleration of corbel 2

从图20、21分析可知，以140 km/h速度运行时，采用新型走行机构的单悬浮架磁浮系统，车体与托臂2加速度并没有发生突变现象，说明系统能够实现较好的稳定悬浮；同时与乘坐舒适性密切相关的车体加速度最大值仅为0.5 m/s2，满足垂向加速度低于1 m/s2的要求，同时车体垂向加速度试验结果与仿真结果较为接近，进一步验证了模型简化的合理性。

5 结 论

为进一步提高中低速磁浮列车的综合竞争力，本文提出一种全新的设计方案并得出以下结论：

(1) 新设计的中低速磁悬浮列车在直线线路段能够实现140 km/h的稳定运行，具有较好的乘坐舒适性，满足直线段的运行要求。

(2) 新设计的中低速磁悬浮列车在空载情况下能够实现以30 km/h的运行速度顺利通过半径为50 m的弯道，且具有较好的乘坐舒适性与悬浮稳定性，满足弯道段的运行要求。

[1] YAGHOUBI H, ZIARI H. Development of a maglev vehicle/guideway system interaction model and comparison of the guideway structural analysis with railway bridge structures[J].Journal of Transportation Engineering,2010, 137(2): 140-154.

[2] FUJIWARA O, WANG J, ISHIMOTO S. Environment Impact Assessment on the TOBU-KYURYO-LINE (HSST System) in Japan[C]//Proceedings of the 18th InternationalConference on Magnetically Levitated Systemsand Linear Drives Maglev. Atsugi, 2004: 632-635.

[3] 邓永权，罗世辉，梁红琴.基于SIMPACK的磁悬浮车辆耦合动力学性能仿真分析[J].交通运输工程学报，2007，7(1)： 13-16.

DENG YongQuan, LUO Shihui, LIANG Hongqin. Simulation model of maglev couping dynamics performance based on SIMPACK[J]. Journal of Traffic and Transportation Engineering, 2007, 7(1): 13-16.

[4] 叶学艳，赵春发，翟婉明.低速磁浮车辆动力学建模与导向机构仿真分析[J].交通运输工程学报，2007，7(3)： 7-10.

YE Xueyan, ZHAO Chunfa, ZHAI Wanming. Dynamics modeling of low-speed maglev vehicle system and simulation of its guidance mechanisms[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 7-10.

[5] 翟婉明，赵春发.磁浮车辆/轨道系统动力学(Ⅰ)——磁/轨相互作用及稳定性[J].机械工程学报，2005，41(7)： 1-10.

ZHAI Wanming, ZHAO Chunfa. Dynamics of vehicle/guideway systems(Ⅰ)—magnet/rail interaction and system stability[J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 1-10.

[6] LEE J S, KWO S D, KIM M Y, et al. A parametric study on the dynamics of urban transit maglev vehicle running on flexible guide-way bridges[J]. Journal of Sound and Vibration, 2009, 3(28): 301-317.

[7] YAU J D.Vibration control of maglev vehicles traveling over a flexible guideway[J]. Journal of Sound and Vibration 2009, 3(21): 184-200.

[8] 赵志苏，尹力明，罗坤.磁悬浮列车转向机构运动分析与设计[J]. 机车电传动，2000，6(4)： 10-13.

ZHAO Zhisu, YIN Liming, LUO Kun. Motion analysis and design for yawing mechanism of maglev vehicle[J]. Electric Drive for Locomotive, 2000, 6(4): 10-13.

[9] 赵春发，翟婉明.磁浮车辆轨道系统动力学(Ⅱ)——建模与仿真[J].机械工程学报，2005，41(8)： 163-175.

ZHAO Chunfa, ZHAI Wanming. Dynamics of maglev vehicle/guideway system(Ⅱ)—modeling and simulation[J]. Chinese Journal of Mechanical Engineering, 2005, 41(8): 163-175.

[10] REN S, ROMEIJN A, KLAP K. Dynamic simulation of the maglev vehicle/guideway system[J]. Journal of Bridge Engineering, 2009, 15(3): 269-278.

[11] SHI J, WANG Y J. Dynamic response analysis ofsingle-span guideway caused by high speed maglev train[J]. Latin American Journal of Solids and Structure, 2011, 8(3):

213-228.

[12] 洪华杰，李杰. 磁浮系统模型中用弹簧阻尼器替代控制器的等效性分析[J]. 国防科技大学学报，2005，27(4)： 101-105.

HONG Huajie, LI Jie. The analysis of the equivalence of substitution the controllers with the spring-dampers in maglev system model[J]. Journal of National University of Defense Technology, 2005, 27(4): 101-105.

[13] MEISINGER R.Control systems for flexible maglev vehicles riding over flexible guideyway[J]. Vehicle System Dynamics, 1975, 4(2/3): 200-202.

[14] BREZINA W, LANGERHOLC J. Lift and side force on rectangular pole pieces in two dimensions[J]. Journal of Applied Physics, 1974, 45(4): 1869-1872.

[15] ZHAO C F, ZHAI W M. Maglev vehicle/guideway vertical randomresponse and ride quality[J]. Vehicle System Dynamics, 2002, 38(3): 185-210.

[16] 张耿，李杰，杨子敬. 低速磁浮轨道不平顺功率谱研究[J]. 铁道学报，2011，33(10)： 73-78.

ZHANG Geng, LI Jie, YANG Zijing. Estimation of power spectrum density track irregularities of low-speed maglev railway lines[J]. Journal of The China Railway Society, 2011, 33(10): 73-78.

[17] 林志雄，周岱. 上海磁浮列车轨道梁系统简述[J]. 中国铁道科学，2003，24(1)：104-107.

LIN Zhixiong, ZHOU Dai. The system briefly of maglev-train track beam in Shanghai[J]. China Railway Science, 2003, 24(1): 104-107.

[18] 张卫华.机车车辆动态模拟[M].北京：中国铁道出版社，2006:283-291.

[19] 梁鑫，罗世辉，马卫华.基于相似原理的磁浮车桥耦合振动研究[J].铁道科学工程学报，2014, 11(3)： 31-36.

LIANG Xin,LUO Shihui,MA Weihua.Study on coupling vibration of maglev vehicle-bridge based on the similarity theory[J].Journal of Railway Science and Engineering,2014, 11(3): 31-36.

Adynamicsimulationanalysisofnewmaglevtrains

WANG Keren1, LUO Shihui1, ZONG Lingxiao2, MA Weihua1

(1.Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China;2. China Railway Eleven Bureau Group Co., Ltd., Wuhan 430061, China)

To explore the dynamic characteristics of the new type of maglev trains, a new model with 56 degrees of freedom was established and simulated, and a single suspension frame model was used as a test rig for ride comfort. The simulation results show that the new type of maglev train can be operated stably at the speed of 140 km/h on a straight line, the lateral acceleration of the car body is less than 0.2 m/s2; the vertical acceleration of the car body is less than 0.5 m/s2; the new type of maglev train can stably pass through a curve with the radius of 50 m at the speed of 30 km/h; the largest car body roll angle is less than 0.04 rad; lateral acceleration of the car body is less than 1 m/s2; vertical acceleration of car body is less than 0.1 m/s2; dynamic variation of levitation clearance is only 0.5 mm. The test results show that car body vertical acceleration related to ride comfort is about 0.5 m/s2at the speed of 140 km/h.

new type of maglev trains; running mechanism; dynamics simulation; ride comfort

国家重点研发计划资助项目(2016YFB1200601-A03；2016YFB1200602-13)；国家重点实验室自主研究课题(2016TPL_T03)

2016-09-23 修改稿收到日期： 2016-11-24

汪科任 男，博士生，1987年生

罗世辉 男，博士，教授，1964年生

E-mail：shluo@swjtu.cn

U270.11

A

10.13465/j.cnki.jvs.2017.20.005