基于双冲击特征的无转速计混合陶瓷球轴承剥落区宽度估计

康 伟， 郭 瑜， 伍 星

(昆明理工大学 机电工程学院 云南省高校振动与噪声重点实验室，昆明 650500)

基于双冲击特征的无转速计混合陶瓷球轴承剥落区宽度估计

康 伟， 郭 瑜， 伍 星

(昆明理工大学 机电工程学院 云南省高校振动与噪声重点实验室，昆明 650500)

首先介绍了一种基于振动信号分析的滚动球轴承剥落区宽度估计的方法，该方法可根据振动信号中的双冲击特征间隔和所在转轴的转速，完成对剥落区宽度的估计，但转速计的安装易受工况条件的限制，对此提出了一种基于滚动轴承剥落故障对应冲击特征的无转速计剥落区宽度估计方法，该方法通过振动信号中整周期的冲击次数实现转速估计,结合平均双冲击特征实现了无需转速计的混合陶瓷球轴承的剥落区宽度估计，使该方法更适合于工程应用。试验结果表明，所提方法可对混合陶瓷球轴承剥落区宽度进行有效估计。

剥落；混合陶瓷球轴承；双冲击特征

混合陶瓷(Si3N4)球轴承[1]在高速电主轴中得到广泛应用，其故障为高速电主轴失效的主要形式之一。因此，开展混合陶瓷球轴承故障特征提取和故障诊断研究有重要意义。同常规滚动球轴承类似，混合陶瓷球轴承的主要失效形式也是疲劳剥落[2]。值得注意的是，滚动轴承故障程度的大小可由剥落区宽度来反映，但对剥落区宽度的测量，目前可用的方法有限，通常只能将轴承拆卸后进行测量，操作不便。近来，一种基于振动信号分析的滚动球轴承剥落区宽度估计的方法[3]被提出，即通过提取故障信号中的双冲击特征，获取双冲击之间的时间间隔，再结合转速，实现对剥落区宽度的测量。该方法的提出，为实现运行工况下的剥落区宽度估计提供了可能。以外圈剥落故障为例，当滚动体通过外圈剥落区时，在进入点和退出点均会产生相应的冲击，形成双冲击特征[4]。Sawalhi等[5]提出了一种基于最小熵解卷积(MED)滤波的故障特征增强方法，对滚动球轴承故障双冲击特征的提取有较好的效果。本文结合上述方法，研究介绍了一种基于振动信号分析的滚动球轴承剥落区宽度估计的方法。需要指出的是，该方法不仅需要采集振动信号，还需要采集实时转速信号。但实际工况中，受安装条件等限制，转速信号的获得不能得到保证，影响了该方法的工程应用。针对上述不足，本文提出了一种基于冲击特征的无转速计剥落区宽度估计方法。以人造故障混合陶瓷球轴承为试验对象，分别使用Randall剥落区宽度估计方法和新方法对剥落区宽度进行估计，结果表明，所提方法可对剥落区宽度进行有效估计。

1 滚动轴承剥落故障双冲击特征

1.1 双冲击特征简介

滚动轴承剥落故障双冲击特征由Epp发现，描述的是具有外圈(或内圈)剥落故障的滚动轴承在运行时，滚动体通过剥落区所产生的一种固有现象。之后Dowling[6]和Randall都对其进行了相关研究，进一步验证了双冲击特征的存在。但是，在双冲击特征的构成上，Epp认为其由一个阶跃响应和一个脉冲响应构成，郭瑜等[7]则认为其由两个脉冲响应构成，Randall通过对外圈剥落故障滚动球轴承振动信号的双冲击特征分离提取的研究，得出了与Epp更加近似的观点，即：双冲击特征由一个阶跃响应和一个脉冲响应所构成。以外圈故障为例，如图1所示，双冲击特征产生原理可解释为：假设轴承外圈固定，内圈跟随转轴做顺时针转动，当滚动体进入剥落区前边缘时，通过剥落区的滚动体的旋转中心变为A点，滚动体与滚道间发生非瞬时的去应力，产生一阶跃响应；当滚动体经过剥落区一半时，通过剥落区的滚动体的旋转中心由A点变为B点，其回转方向也同时发生改变，滚动体对剥落区后边缘产生突然地瞬时冲击，产生一脉冲响应；当滚动体完全通过剥落区时，又恢复正常承载状态。然而，振动信号中的双冲击特征由于受到噪声和信号衰减的影响，难以直接观察，须通过信号处理方法进行分离和提取，才能清晰获得。

图1 外圈剥落故障引起双冲击特征示意Fig.1 Double impulses illusion causedby the spall of bearing outer ring

1.2 双冲击特征提取

当滚动轴承存在外圈(或内圈)剥落故障的时候，其滚动体在通过故障区时会产生周期性双冲击特征，可激起轴承及其周围结构的固有振动。振动信号中的双冲击特征，由于受到传递路径和环境中的强噪声影响，不易直接在原始振动信号中进行观察。利用基于最小熵解卷积(MED)滤波的故障特征增强方法可有效提取双冲击特征，其基本步骤如图2所示。

图2 双冲击特征提取原理框图Fig.2 Extraction procedure of double impulses

首先，使用AR预白化的方法处理原始信号，去除振动信号中的确定性信号的干扰，得到包含明显故障特征的残余信号。该过程可用下式表示

(1)

式中：εk为含有故障特征的残余信号；p为AR模型的阶次(阶次大小可根据峭度原则确定[8])；ai为AR模型的参数；x为振动信号，下标k表示第k点。

其次，使用结合谱峭度的MED滤波方法对残余信号做进一步处理，解卷积传递路径的影响，获取显著抑制频带外噪声干扰影响的振动信号(由于本文主要是估计剥落区宽度，故对该方法不做详细介绍，详情可参见文献[5])。

最后，使用基于Hilbert变换的包络提取方法对信号进行解调，获取包络信号并提取信号的双冲击特征。

2 剥落区宽度估计

滚动轴承的疲劳效应会引发其滚道或滚动体的剥落，进而导致滚动轴承的失效。在实际生产中，滚动轴承在发生剥落故障的初期，仍可继续工作一段时间，若过早对滚动轴承进行维护和更换，将增加生产成本。因此，开展研究一种有效的故障评测方法有重要意义。

2.1 基于双冲击特征的剥落区宽度估计方法

美国NASA通过检测润滑油中的碎屑来评判滚动轴承的故障发展程度[9]，取得了一定的效果，但也存在造价高昂等不足之处，不利于工程运用。剥落区宽度的大小可反映轴承损伤的剧烈程度，对轴承剩余寿命的预测十分重要。Randall研究完善了双冲击特征的相关理论，并把双冲击特征用于剥落区宽度的估计当中，提出了基于振动信号双冲击特征的剥落区宽度估计方法，可有效估计剥落区宽度大小。

由双冲击特征的形成原理可知，据双冲击特征所计算的时间间隔实际上只是滚动体通过剥落区宽度一半时所用的时间。Randall指出，剥落区宽度l0(mm，如图1所示)与双冲击间隔Ti(单位为点，注：采样率一定的情况下，采样时刻t所对应的点数是确定的，为便于表示，文中直接使用采样点数表示其对应的采样时刻，故双冲击间隔既为对应的脉冲响应时刻与阶跃响应时刻之间的间隔点数)存在如下关系

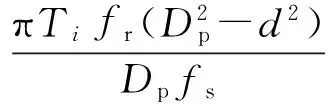
(2)

式中：fr是转轴的转速，Hz；fs是采样频率，Hz；Dp是滚动轴承的节圆直径，mm；d是滚动轴承滚动体的直径，mm。

上述关系式的形成可由以下步骤实现(以外圈剥落故障为例)。

外圈故障剥落区宽度为l0(mm)的滚动轴承，单个滚动体通过剥落区的时间t(s)可以表示为

(3)

式中：D0是滚动轴承的外滚道直径，mm；fc是保持架的转速，Hz。

外滚道直径D0可写成如下形式

D0=Dp+d

(4)

式中：Dp是滚动轴承的节径，mm。

保持架的转速fc(即：滚动体的公转速度)可按下式计算[10]

(5)

式中：α是滚动体与内外滚道的夹角；fi是滚动轴承内圈的转速，Hz；fo是滚动轴承外圈的转速，Hz。

假设滚动轴承的接触角α=0°，且外圈固定，内圈跟随转轴转动，则保持架的转速为

(6)

将式(2)与式(6)代入式(3)可得滚动体通过剥落区的时间t，如下所示

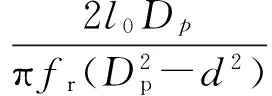
(7)

振动信号中，采样点数Ts与采样时刻t存在如下关系

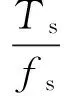
(8)

由于剥落区宽度对应的采样点数Ts为双冲击间隔点数Ti的两倍，故整理式(7)可得

(9)

2.2基于双冲击特征的无转速计剥落区宽度估计方法

由Randall提出的剥落区宽度估计方法可知：在对滚动球轴承剥落区宽度进行估计时， 除了计算双冲击特征间隔外，还需要测量转轴的转速。上文已经提到，受限于工况条件，转速计安装受到限制，不利于该方法的工程应用。因此，本文提出了一种基于双冲击特征的无转速计剥落区宽度估计方法。

(1)双冲击特征间隔的选取：根据以上提到的双冲击特征提方法，能有效分离提取振动信号中的双冲击特征。但考虑到选取双冲击间隔时间时，需克服偶然因素的影响，取多个双冲击特征间隔时间的平均值更加合理。但多个双冲击间隔的提取存在计算量大这一不足，针对这一问题，本文提出了一种半自动的双冲击特征间隔选择方法，帮助快速选取包络信号中的双冲击特征时间间隔。具体实施过程如下：首先，通过一个脉冲响应阈值，将包络信号中的所有脉冲响应特征挑选出来，因为脉冲响应比阶跃响应更加明显；其次，为避免包络信号中脉冲响应特征前后存有干扰阶跃响应特征的峰值信号，需在脉冲响应特征前将部分信号置零和脉冲响应特征后将部分信号置零；最后，设定一阶跃响应阈值，对置零操作后的包络信号进行双冲击特征间隔提取。

(2)无转速计剥落区宽度估计： 首先，使用基于MED的双冲击特征增强方法对原始振动信号中的双冲击特征进行增强，获取双冲击特征明显的振动信号。

然后，根据双冲击特征信号，利用上文提到过的双冲击特征间隔选取方法提取信号中的双冲击特征位置信息，计算平均双冲击特征间隔和滚动轴承旋转一圈的时间间隔。当滚动轴承存在外圈剥落故障时，任意一个滚动体沿外滚道滚过一圈时，其余滚动体也将沿外滚道滚过一圈，在此过程中，一共会产生N个双冲击特征。图3中，ai(i=1,2,…,N)表示双冲击特征中的第i个阶跃响应特征，bi(i=1,2,…,N)表示双冲击特征中的第i个脉冲响应特征。因此，滚动轴承旋转一圈所用时间可表示为第i个脉冲冲击响应时间与第i+N个脉冲冲击响应时间的间隔(或第i个阶跃冲击响应时间与第i+N个阶跃冲击响应时间的间隔)，由于脉冲响应比阶跃响应更加明显且更易提取，故选取脉冲响应时间计算滚动轴承旋转一圈的时间。

最后，根据下式计算剥落区宽度，完成故障剥落区宽度的估计。

(10)

式中：tbi(i=1,2,…,N)为双冲击特征中脉冲响应特征对应的采样点数；N为滚动轴承的滚动体个数。式(10)的推导过程如下。

滚动轴承外圈故障剥落区宽度l0(mm)与外圈滚道周长之比c可表示为

(11)

滚动体沿滚动轴承外滚道转过一圈所产生的双冲击间隔均值与转动一圈所用时间的比值c1可表示为

(12)

根据双冲击特征间隔点数Ti为滚动体通过剥落区宽度一半的时间，可得如下等式

c=2×c1

(13)

将式(11)与式(12)代入式(13)并整理得，滚动轴承外圈故障剥落区宽度l0(mm)与双冲击特征时间间隔(点数)存在以下的关系

(14)

由式(14)可以看出，该方法完全基于振动信号中的双冲击特征估计剥落区宽度，无需安装转速计，易于工程应用。上述无转速计剥落区宽度估计方法可用原理框图4表示。

图4 无转速计剥落区宽度估计原理框图Fig.4 Evaluation procedure of spall size without speed meter

3 试验验证

本文采用QPZZ-Ⅱ型故障模拟试验台(如图5所示)对外圈剥落故障混合陶瓷球轴承进行振动分析试验，试验参数如下：故障轴承型号为6205，外圈故障尺寸分别为1.237 mm、2 mm和2.16 mm(以故障尺寸为1.237 mm的混合陶瓷球轴承为例，如图6所示)；安装轴转速：646.75 r/min；数据采集设备为NI USB9215，采样率为100 kHz；加速度传感器型号为DH112，灵敏度为5.33 pC/(m·s-2)，安装位置为轴承座。试验所采集原始振动信号如图7所示。

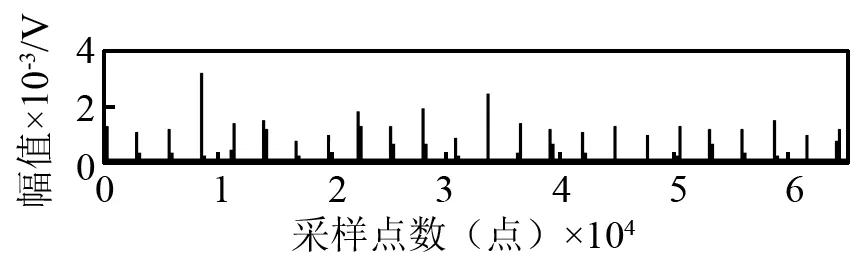
首先，对采集到的原始振动信号首先进行双冲击特征提取，得到图8所示的双冲击特征包络信号。任意选取其中一个双冲击特征进行局部放大，得到图9所示的局部放大原始振动信号和图10所示的局部放大双冲击特征信号，由图10可得，不同外圈故障尺寸的双冲击特征均被有效提取。

然后，利用上文中提出的双冲击特征间隔选取方法从双冲击特征包络信号中提取双冲击时间间隔，并将对应的阶跃响应点和脉冲响应点表示出来，如表1、表2和表3所示(注：各表中，采样时刻和双冲击特征间隔单位为点)。

图5 QPZZ-Ⅱ型试验台Fig.5 QPZZ-Ⅱ test rig

图6 1.237 mm剥落故障混合陶瓷球轴承外圈Fig.6 Hybrid ceramic ballbearing outer race withthe fault size 1.237 mm

(a) 1.237 mm外圈故障

(b) 2 mm外圈故障

(a) 1.237 mm外圈故障

(b) 2 mm外圈故障

(c) 2.16 mm外圈故障图8 双冲击特征包络信号Fig.7 Double impulses envelope signal

(a)1.237 mm外圈故障

(b) 2 mm外圈故障

(c) 2.16 mm外圈故障图9 原始振动信号局部放大Fig.9 The local amplification of raw vibration signal

(a)1.237 mm外圈故障

(b)2 mm外圈故障

(c)2.16 mm外圈故障图10 双冲击特征信号局部放大Fig.10 The local amplification of double impulses envelope signal表1 1.237 mm外圈故障双冲击特征信息提取Tab.1 Double impulse information extractionof 1.237 mm outer race faults

阶跃响应时刻tai脉冲响应时刻tbi双冲击特征时间间隔Tii=15664576399i=28465855893…………i=9279032799794i=10306963078690

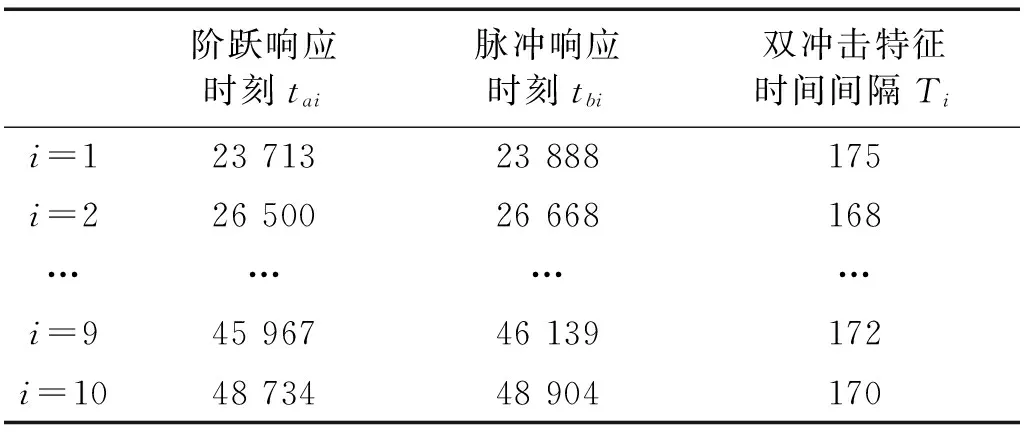
表2 2 mm外圈故障双冲击特征信息提取Tab.2 Double impulse information extractionof 2 mm outer race faults

表3 2.16 mm外圈故障双冲击特征信息提取Tab.3 Double impulse information extractionof 2.16 mm outer race faults

最后，利用Randall估算公式和新提出的估算公式分别对滚动轴承的剥落区宽度进行预估。计算结果如表4、表5和表6所示(注：各表中，Ti为双冲击特征间隔，单位：点；fr为转轴转速，单位：Hz；剥落区宽度尺寸单位：mm)。

表4 1.237 mm外圈故障剥落区宽度预估结果Tab.4 Spall size calculation of 1.237 mm outer race faults

表5 2 mm外圈故障剥落区宽度预估结果Tab.5 Spall size calculation of 2 mm outer race faults

表6 2.16 mm外圈故障剥落区宽度预估结果Tab.2 Spall size calculation of 2.16 mm outer race faults

试验结果表明，Randall剥落区宽度估计方法和新方法均能完成故障混合陶瓷球的剥落区尺寸估计，但新方法并不需要安装转速计。

4 结 论

针对滚动轴承剥落区大小难以有效在线提取这一问题，本文介绍了Randall剥落区宽度预估方法，并针对工况中滚动轴承所在转轴速度不便测量这一不足，提出了一种无转速计的剥落区宽度预估方法。以外圈人工故障混合陶瓷球轴承作为实验对象，利用Randall剥落区宽度预估方法和新提出的剥落区宽度预估方法同时对该故障剥落区进行宽度估计，结果表明所提方法与原方法一样有效，但新方法避免了转速计安装，更加适合于工程应用。

[1] 蒋喜，刘宏昭. 混合陶瓷球轴承的选型研究[J]. 西安理工大学学报，2012，28(1)： 33-38.

JIANG Xi, LIU Hongzhao. Selection of the hybrid ceramic ball bearings[J]. Journal of Xi’an University of Technology, 2012, 28(1): 33-38.

[2] 蒋喜，吴国庆，陈晓阳. 氮化硅陶瓷球滚动接触疲劳寿命模型[J]. 机械工程学报，2008，44(2)： 37-42.

JIANG Xi, WU Guoqing, CHEN Xiaoyang. Tensile stress life model for rolling contact fatigue of silicon nitride ceramic balls [J]. Chinese Journal of Mechanical Engineering, 2008, 44(2): 37-42.

[3] SAWALHI N, RANDALL R B. Vibration response of spalled rolling element bearings: observations, simulations and signal processing techniques to track the spall size[J]. Mechanical Systems and Signal Processing，2011，25(3)： 846-870.

[4] EPPS I K. An investigation into vibrations excited by discrete faults in rolling element bearings[D]. Christchurch:The University of Canterbury, 1991.

[5] SAWALHI N, RANDALL R B, ENDO H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J]. Mechanical Systems and Signal Processing，2007，21(6)： 2616-2633.

[6] DOWLING M J. Application of non-stationary analysis to machinery monitoring[J]. IEEE International Conference on Acoustics, 1993, 1： 59-62.

[7] 郭瑜，郑华文，高艳，等. 基于谱峭度的滚动轴承包络分析[J]. 振动、测试与诊断，2011，31(4)： 517-521.

GUO Yu, ZHENG Huawen, GAO Yan,et al. Envelop analysis of rolling bearing based on spectral kurtgoram[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(4): 517-521.

[8] ENDO H, RANDALL R B. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J]. Mechanical Systems and Signal Processing, 2007, 21: 906-919.

[9] DEMPSEY P J, CERTO J M, MORALES W. Current status of hybrid bearing damage detection[J]. Tribology Transactions, 2005, 48(3): 370-376.

[10] 杨国安. 机械设备故障诊断实用技术丛书 滚动轴承故障诊断实用技术[M]. 北京：中国石化出版社，2012.

Spallsizeestimationoffaultyhybridceramicballbearingswithoutaspeedmeterbasedondoubleimpulses

KANG Wei, GUO Yu, WU Xing

(Key Lab. of Vib. & Noise under Ministry of Education of Yunnan Province, Faculty of Mechanical and Electrical Engineering,Kunming University of Science and Technology, Kunming 650500, China)

A method based on vibration signal was introduced for evaluating the spall size of rolling ball bearings, which utilizes the interval measurement of double impulses generated by the spall and the rotor speed of the bearing mounted shafts. However, the measurement of rotor speed is not convenient under some working conditions. To solve this issue, a method based on double impulses was proposed without a speed meter. The rotor-speed estimated by counting the number of impulses in a full rotating cycle of the shaft. By combining the rotor speed and average double-impulse intervals, the new method realizes spall size estimation without a speed meter. It is thus appropriate for engineering applications. Experimental results indicate that the proposed method is valid.

spall; hybrid ceramic ball bearing; double impulses

国家自然科学基金(51365023)

2016-06-15 修改稿收到日期： 2016-08-30

康伟 男，硕士生, 1992年生

郭瑜 男, 教授，博士生导师, 1971年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.20.001