两广义Gaussian分布之间的最小Kullback-Leibler距离

朱成莲

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

两广义Gaussian分布之间的最小Kullback-Leibler距离

朱成莲

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

在Kullback-Leibler距离的基础上,对Kullback-Leibler距离进行了改进,给出了最小的Kullback-Leibler距离,并讨论了它的性质.探讨了两个不同概率密度函数的差异程度,得到了广义Gaussian分布最小的Kullback-Leibler距离,并作为特例得到了Laplacian分布和Gaussian分布最小的Kullback-Leibler距离.

广义高斯分布; Kullback-Leibler距离; Laplacian分布

0 引言

由Stacy[1]提出的广义Gaussian (GGD)是一类以Laplacian分布、Gaussian分布为特例,以δ函数和均匀分布为极限形式的对称分布,它在信号处理、图像处理和拟合非Gaussian噪声等领域有着广泛的应用.Joshi和Fischer[2]采用零均值的GGD来拟合DCT交流系数; Do和Vetterli[3]用GGD来逼近小波系数的边缘分布;Walden和Hosken[4]在研究地震信号时发现,主反射系数序列的振幅分布可以用GGD逼近.从已知样本去估计母体的分布,或者推断分布的特征,对于同样的母体分布,当用几种不同的统计方法获得了母体的两个估计分布后,人们往往要对所求得的分布进行比较,为此,统计学引入了许多度量两个分布差异的距离,如Kullback-Leibler距离,Pearson-χ2距离和全变差距离等.

近年来,概率密度函数的Kullback-Leibler距离在学术界备受关注,在讨论极值分布的大样本问题、分布函数估计的收敛性、用不同算法借补有缺失数据的分布估计的收敛速度问题时,都使用Kullback-Leibler距离[5-7].从定义形式来看,其缺乏对称性、不具备距离三角不等式性,但由于其确实能够在某种程度上刻划两个密度函数的差异程度,因而被统计学广泛采用. 本文将Kullback-Leibler距离定义进行了推广,定义了最小Kullback-Leibler距离.从定义形式上看,并不难理解,最小Kullback-Leibler距离是将两个概率密度函数间的Kullback-Leibler距离求较小值,但它的意义在于克服了Kullback-Leibler距离没有对称性的缺陷.本文探讨了两个广义Gaussian分布密度函数的差异程度,得到了广义Gaussian分布最小Kullback-Leibler距离,并作为特例得到了Laplacian分布、Gaussian分布的最小Kullback-Leibler距离,这些结果为应用打下了较好的基础.

1 相关定义及性质

定义1[8]如果随机变量X的概率密度函数为

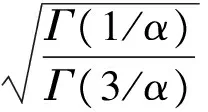
定义2[8]如果随机变量X的概率密度函数为

则称X服从Laplacian分布,记为L(μ,σ).

定义3[8]如果随机变量X的概率密度函数为

则称X服从Gaussian分布,记为G(μ,σ).

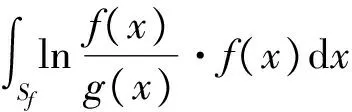
显然Kullback-Leibler距离d(f,g)不符合传统的距离公理,但也有与距离公理相类似的结果.

定理1 设f(x)>0,g(x)>0是两个概率密度函数,那么d(f,g)具有如下性质:

1)d(f,g)≥0;

3)d(f,g)=0⟺E(lnf(x))=E(lng(x))⟺f(x)=g(x);

由定理1的1)、3)知d(f,g))确实能刻画f(x)与g(x)的差异, Kullback-Leibler距离d(f,g)与距离公理相比较不满足对称性且三角形不等式也未必成立.现利用d(f,g),可以构造出最小的Kullback-Leibler距离.

定义5 设两个随机变量X1,X2的概率密度函数分别为f(x)、g(x),并且f(x)>0,g(x)>0,若d(f,g)和d(g,f)都存在,记dmin(f,g)=min(d(f,g),d(g,f)),则称dmin(f,g)为两个概率密度函数f(x)和g(x)之间最小的Kullback-Leibler距离.

根据dmin(f,g)的定义及定理1,有如下定理．

定理2 设f(x)>0,g(x)>0是两个概率密度函数,那么dmin(f,g)有

1)dmin(f,g)≥0;

2)dmin(f,g)=dmin(g,f);

3)dmin(f,g)=0⟺f(x)=g(x);

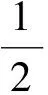
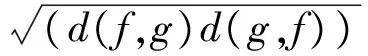
由定理2可以看出,dmin(f,g))与d(f,g)相比较,dmin(f,g)除了具有d(f,g)的性质外, 还克服了d(f,g)不具有对称性的缺点.因此, 认为dmin(f,g)来刻画两个密度函数的差异时, 更为合理.

2 两个广义Gaussian分布之间的Kullback-Leibler的距离

定理3 设f(x)是广义Gaussian分布GGD(μ,α,β1)的概率密度函数,g(x)是广义Gaussian分布GGD(μ,α,β2)的概率密度函数,则

由于

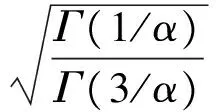
所以

定理4 设f(x)是广义Gaussian分布GGD(μ,α,β1)的密度函数,g(x)是广义Gaussian分布GGD(μ,α,β2)的密度函数,则

定理5 设f(x)是广义Gaussian分布GGD(μ,α,β1)的密度函数,g(x)是广义Gaussian分布GGD(μ,α,β2)的密度函数,则

证明由于

令

对上式关于x求导可得

所以,F(x)在区间(0,+∞)上为减函数.

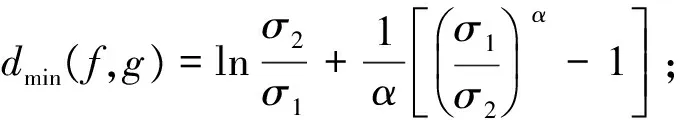
因此

定理6 设f(x)是广义Gaussian分布GGD(μ,α1,β1)的密度函数,g(x)是广义Gaussian分布GGD(μ,α2,β2)的密度函数,则

因此

定理7 设f(x)是广义Gaussian分布GGD(μ,α1,β1)的密度函数,g(x)是广义Gaussian分布GGD(μ,α2,β2)的密度函数,则

定理8 设f(x)是广义Gaussian分布GGD(μ,α1,β1)的密度函数,g(x)是广义Gaussian分布GGD(μ,α2,β2)的密度函数

则

在定理3、定理5中,取α=1,则可以得到Laplacian分布的Kullback-Leibler距离的结论.

推论2 设f(x)是拉普拉斯分布L(μ,σ1)的密度函数,g(x)是拉普拉斯分布L(μ,σ2)的密度函数(其中σ1>0,σ2>0),则

在定理3、定理5中,取α=2,则可以得到Gaussian分布的Kullback-Leibler距离的结论:

推论4 设f(x)是Gaussian分布G(μ,σ1)的密度函数,g(x)是Gaussian分布G(μ,σ2)的密度函数(其中σ1>0,σ2>0),则

3 几个距离间的关系

定理910]以下讨论的距离都存在,则

1) 当f(x)≥g(x)时,d(f,g)≤d2(g,f);

2)V2(f,g)≤d2(f,g);

有d(f,g),d(g,f)及min{d(f,g),d(g,f)}的定义易得如下定理.

定理10 如果以下讨论的距离都存在,则

1) min{d(f,g),d(g,f)}≤d(f,g)≤max{d(f,g),d(g,f)};

[1] Stacy E W. A generalization of gamma distribution[J].Ann Math Stat,1962(28):1187-1192.

[2] Joshi R J, Fischer T R. Comparison of generalized Gaussian and laplacian modeling in DCT image coding[J].IEEE Trans, on signal processing letters,1995,2(5):81-82.

[3] Do M N, Vetteli M. Wavelet-based texture retrieval using generalized Gaussian density and Kullback-leibler distance[J].IEEE Trans,2002,11(2):146-158.

[4] Walden A T,Hosken J W J. The nature of the non-Gaussianity of primary reflection coefficients and its significance for deconvolution[R].The 47th meeting of the EAEG,Budapest,1985,1038-1066.

[5] Robert G O, Shau S K. Updating Schemes,Correlation Structure,Blocking and Parameterization for the Gibbs Sampler[J]. J R Statist Soc B,1997(59):291-317.

[6] Liu S J, Wong W H, Kong A. Correlation Structure and Convergence Rate of the Gibbs Sampler with Various Scans[J].J R Statist Soc B,1995(57):157-169

[7] Reiss R D. Approximate Distributions of Order Statistics[M].New York: Springer,1980.

[8] 金秀岩. 广义Gaussian分布Pearson-χ2距离及其渐近性[J].西南师范大学学报,2007,33(5):1040-1045.

[9] 蔡择林,李开灿. 常见分布的最大Kullback-Leibler距离[J].武汉大学学报,2007,53(5):513-517.

[10] 李开灿. Pearson-χ2距离的若干性质[J]. 数学的实践与认识,2003,33(1):49-53.

[11] 李开灿,孟朝玲.χ2分布、t分布和F分布的一致渐进正态性[J].北京印刷学院学报,2004,12(3):30-33.

TheMinimumKullback-LeiblerDistancebetweentwoGeneralizedGaussianDistribution

ZHU Cheng-lian

(School of Mathematical Science, Huaiyin Normal University, Huaian Jiangsu 223300, China)

In this paper,it gives the exact definition of the minimum Kullback-Leibler distance between two different distribution functions.The properties of the minimum Kullback-Leibler distance are discussed.The difference degree of two different probability density function are discussed.The minimum Kullback-Leibler distance between two different generalized Gaussian distribution are obtained.The minimum Kullback-Leibler distance of Laplacian distribution, Gaussian distribution are derived.

generalized Gaussian distribution; Kullback-Leibler distance; Laplacian distribution

O211.1

A

1671-6876(2017)03-0189-06

[责任编辑李春红]

2017-03-20

国家自然科学基金项目(11401245); 江苏省自然科学基金项目(BK20130412); 淮安市科技支撑(农业)项目(SN13050)

朱成莲(1966-),女,江苏涟水人,副教授,硕士,研究方向为概率论与数理统计. E-mail: hytczcl@126.com