海上丝绸之路航线网络的连通性建模与仿真研究

严南南， 陆 珉， 宗 康

(上海海事大学 物流科学与工程研究院， 上海 201306)

海上丝绸之路航线网络的连通性建模与仿真研究

严南南， 陆 珉*， 宗 康

(上海海事大学 物流科学与工程研究院， 上海 201306)

为推进海上丝绸之路航线网络的建设与完善，基于复杂网络的相关理论，从局部和全局两个角度对不同攻击模式和应对策略下网络的连通性进行了研究.结果表明，海上丝绸之路航线网络在节点随机攻击下的抗毁性较强，而在选择攻击下，网络的连通性较差；对于提高航线网络连通性，甩港策略的效果要更优于重要港口保护策略.同时，不同测度下，对网络连通性影响较大的港口多为东亚和东南亚地区介数较高的港口，在对网络进行连通性优化时，可根据介数确定各个港口在网络中的重要性.

水路运输； 海上丝绸之路； 复杂网络； 航线网络； 连通性

在国际间政治及贸易的新形式下，建设海上丝绸之路是加强国际间的合作与推动经济发展的重要措施[1].而合理高效的航线网络对于国际间进行贸易起到了十分关键的作用，由于天气、灾难等不可抗因素可能导致港口在网络中产生不同程度的影响，进而导致港口失效[2]，估测港口失效对其在网络连通性中的影响程度并提出合理的策略，对于管理与优化海上丝绸之路航线网络，推进海上丝绸之路的建设具有重要意义.

楼春豪[3]发现了海上丝绸之路的机遇与挑战；谭秀杰等[4]基于随机前沿引力模型对海上丝绸之路沿线国家的贸易潜力进行了研究；张林等[5]在全球化和深化南南合作的背景下，分析了海上丝绸之路的战略对策.航线网络方面，赵旭等[6]对海上丝绸之路背景下港口战略联盟的稳定性进行了研究；曾庆成等[1，7]分析了海上丝绸之路航线网络的复杂性及其沿线港口的空间分布特征.BROUER等[8]通过复杂网络的角度对航运网络进行了研究；JIANG等[9]研究了全球集装箱班轮运输网络的连通性.在外文文献中对于一带一路的研究主要表现在历史文化[10]、政治地缘[11]、贸易路线[12]以及区域合作[13]等多个方面.

综上所述，现有研究对海上丝绸之路背景下航线网络的研究较少，对网络连通性的研究则更少.本文中把连通性定义为：海上丝绸之路航线网络的港口节点在遭受随机故障或者故意攻击的情况下，网络全局以及节点间保持连通的能力.基于此，构建了海上丝绸之路航线网络，得出了平均路径长度、最大连通子图的相对大小和网络效率这3种连通性测度在不同攻击模式下的演化曲线， 并分析了不同应对策略下网络连通性的变化，以此为海上丝绸之路的建设、优化管理航线网络提供研究基础和相关理论.

1 研究方法与数据选择

复杂网络是一种可以用来描述自然科学、社会科学和科学工程技术上的相互关联的系统的模型[7].网络中的个体用节点表示，节点与节点之间的联系则可以用边表示[14-15].近年来，多数学者把复杂网络理论应用到海运航线的研究，并在网络的结构特征[16]、鲁棒性[17]、中心性[18]及演化规律[19]等方面做出了许多有影响力的工作.海上丝绸之路航线网络是一个典型的复杂网络[1]，将复杂网络理论应用于海上丝绸之路航线网络的研究，有助于更好的刻画网络结构.

海上丝绸之路航线网络由港口和航线两个基本要素组成，将航线中的每一个港口看成一个节点，两个港口间的直达航线看成边，由此构建航线网络[20].本文选取了世界前十大班轮公司中七家公司的航运数据来构建海上丝绸之路航线网络.跟踪时间为2015年10月～2016年1月.根据相关航线情况，搜集网络中挂靠的205个港口的数据、航线数据以及物流统计数据，使用 MATLAB处理数据并构建205×205的0～1邻接矩阵，刻画出海上丝绸之路航线网络结构，如图1所示.

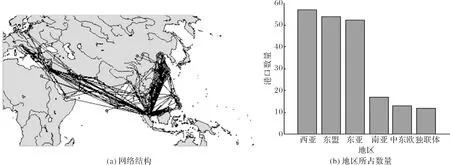
图1 海上丝绸之路航线的网络结构及不同地区的网络数量Fig.1 Network structure of Maritime Silk Road routes and number of regions

2 海上丝绸之路航线网络连通性仿真评估

2.1 连通性测度的设计

本文将反映网络连通性的指标设为对航线网络连通性的测度.测度标准采取网络效率、最大连通子图相对大小和平均最短路径长度.

1) 网络效率.网络中任意两个节点i和j之间的效率εij等于这两个节点间距离dij倒数，网络中所有节点对之间效率的平均值则为整个网络的效率，用E表示，它反映了网络节点间的连通性和网络的整体效率，计算公式为

(1)

2)最大连通子图的相对大小.最大连通子图指的是在一个全连通的网络逐渐遭到破坏后，所有分裂出的子图中规模最大的，其相对大小S定义为最大连通子图的节点数N'与初始状态下网络的总节点数N之比[19]，即S=N'/N，它能直观的反映网络中最大子集团的规模以及网络遭受破坏的程度.

3)平均路径长度.节点i和j之间的距离dij，表示为节点间最短路径所包含的边数，L为网络中所有节点之间距离的平均值，即平均路径长度.反映了网络节点间沟通的难易程度，计算公式如式(2)，其中N为网络的总节点数.

(2)

2.2 连通性评估模型的构建

网络连通性是指网络在遭受不同程度破坏时，其节点间的连接程度.本文采取随机攻击和选择攻击两种模式，攻击某一节点指的是删除与该节点相连的所有边[21].通过构建模型从不同的角度对网络连通性进行评估，发现网络中存在的薄弱点并采取相应的提高连通性的措施.

根据海上丝绸之路航线网络模型、网络连通性测度及攻击策略，构建了海上丝绸之路航线网络连通性评估模型，如图2所示.

A：攻击策略的集合，设A={A1，A2，…，Ai}，Ai指第i种连通性攻击策略；

M：连通性测度的集合，设M={M1，M2，…，Mj}，Mj指第j个的连通性测度；

f：节点破坏的比例；

f(Ai，Mj)：节点在采用攻击策略Ai破坏网络中节点的情况下失效的比例为f时连通性测度Mj的值；

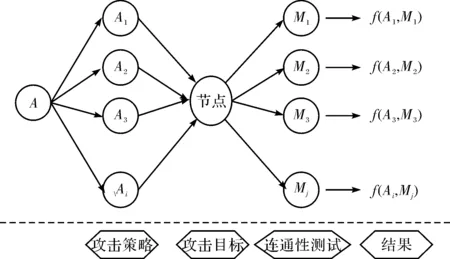
图2 海上丝绸之路航线网络连通性评估模型Fig.2 Connectivity evaluation model of Maritime Silk Road route network

采用上述模型对网络连通性评估的实验过程为： 当采取随机攻击实验时，每次随机在网络中删除一个节点，再次进行网络的连通性测度，循环实验直到网络中的节点删除完毕；当采取选择攻击实验时，删除节点的方式按照节点度、节点介数和接近度从大到小的顺序[22-24]，再次进行网络的连通性测度，循环实验直到网络中的节点删除完毕.由此可以得到不同攻击策略下网络受到不同程度破坏时各个连通性测度的值，从而全面的了解海上丝绸之路航线网络的连通性和稳定性.

2.3 网络连通性仿真评估

1) 图3a演示了平均路径长度在不同失效模式下的变化，随着删除节点数量的增加，网络的平均路径长度逐渐增大.随机攻击曲线缓慢上升，平均路径长度的变化与网络节点的攻击进度成正比；而对于节点度、节点介数和接近度3种攻击方式下.由此可见，选择攻击比随机攻击对网络的破坏程度大.

2) 图3b可以看出，随机攻击下，网络最大连通子图相对大小下降得比较缓慢，基本正比于网络节点的攻击进度；而节点度、节点介数攻击攻击下，删除30%的节点后，网络连通的节点数几乎为0，此时网络已几乎瘫痪.由此可见，网络在随机攻击下抗毁性较强，而在选择攻击情况下，网络较易瘫痪.

3) 图3c可以看出，初始状态下的网络效率为0.332 8，节点度、节点介数攻击攻击下，网络在节点度和节点介数攻击下，前期下降十分迅速，后期下降缓慢；而在随机攻击下，演化曲线缓慢下降，网络效率的变化基本正比于网络节点的攻击进度.网络效率呈现阶梯式下降，大部分度值和介数较小的节点失效时下降缓慢，而较大节点失效时下降迅速，表明度值和介数较大的节点对网络连通性起着十分关键的作用.

图3 不同攻击策略下连通性测度的变化Fig.3 The variation of connectivity measures under different attack strategies

3 海上丝绸之路航线网络的连通性优化研究

从不同方面采用合理的策略对网络进行优化能够有效提高网络的连通性.当港口失效时，根据装卸货物情况采取甩港应对策略，将原本在失效港口卸船的货物转移到下一挂靠港口卸船，再通过后期安排船期将货物运至失效港口[18]；为提高网络的连通性，可以对网络中核心港口实行重点保护，加强港口的维护与保养，提高突发事件下货物的疏散能力，切实保障这类港口的正常、高效运行.甩港和重要港口保护均可以看成是海上丝绸之路航线网络中港口失效的两种应对策略.

3.1 仿真算法的设计

1) 甩港策略.在采取甩港应对策略的仿真实验中，当某个港口失效时，在失效港口的前一个港口和后一个港口的航线上连一条有效边，当次失效港口的前后港口是同一个时，则向后一个港口递推.

2) 重要港口保护策略.重要港口保护策略下的仿真实验中，保护海上丝绸之路航线网络中节点度和节点介数最大的港口使其不受攻击，然后衡量各个连通性测度的变化.

不同应对策略下海上丝绸之路航线网络连通性仿真求解算法流程图如图4所示，其中N指初始港口总数，生成的失效港口序列不包含节点度和节点介数最大的港口.

3.2 3种应对策略下网络连通性比较

图5演示了不同应对策略下平均路径长度的变化，随机攻击下，没有采取策略和重要港口保护策略下的演化曲线是缓慢上升，而甩港策略下的演化曲线是一开始上升十分缓慢，等到删除90%的节点后，曲线迅速上升；没有采取策略和重要港口保护策略下平均路径长度一开始就迅速上升，而甩港策略下的演化曲线在整个过程都处于缓慢上升状态.

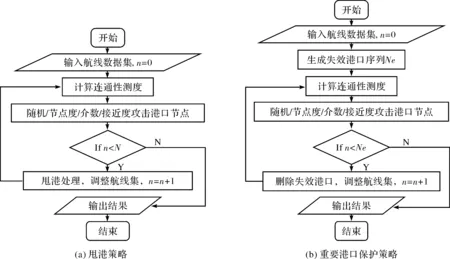
图4 应对策略下网络连通性算法流程图Fig.4 The algorithm flow chart of network connectivity with countermeasures

图6演示了不同应对策略下最大连通子图相对大小的变化，随机攻击下，3种应对策略下网络最大连通子图相对大小下降得比较缓慢；节点度、节点介数攻击下，没有采取策略时删除30%的节点后，网络连通的节点数几乎为0；接近度攻击下，没有采取策略和重要港口保护策略下，35%的节点失效之前，重要港口保护策略下的演化曲线变化较为缓慢，删除35%的节点后，两种应对策略下的演化曲线呈重叠状态；而甩港策略下的演化曲线呈缓慢下降之势，要使网络瘫痪，需删除80%多的节点.

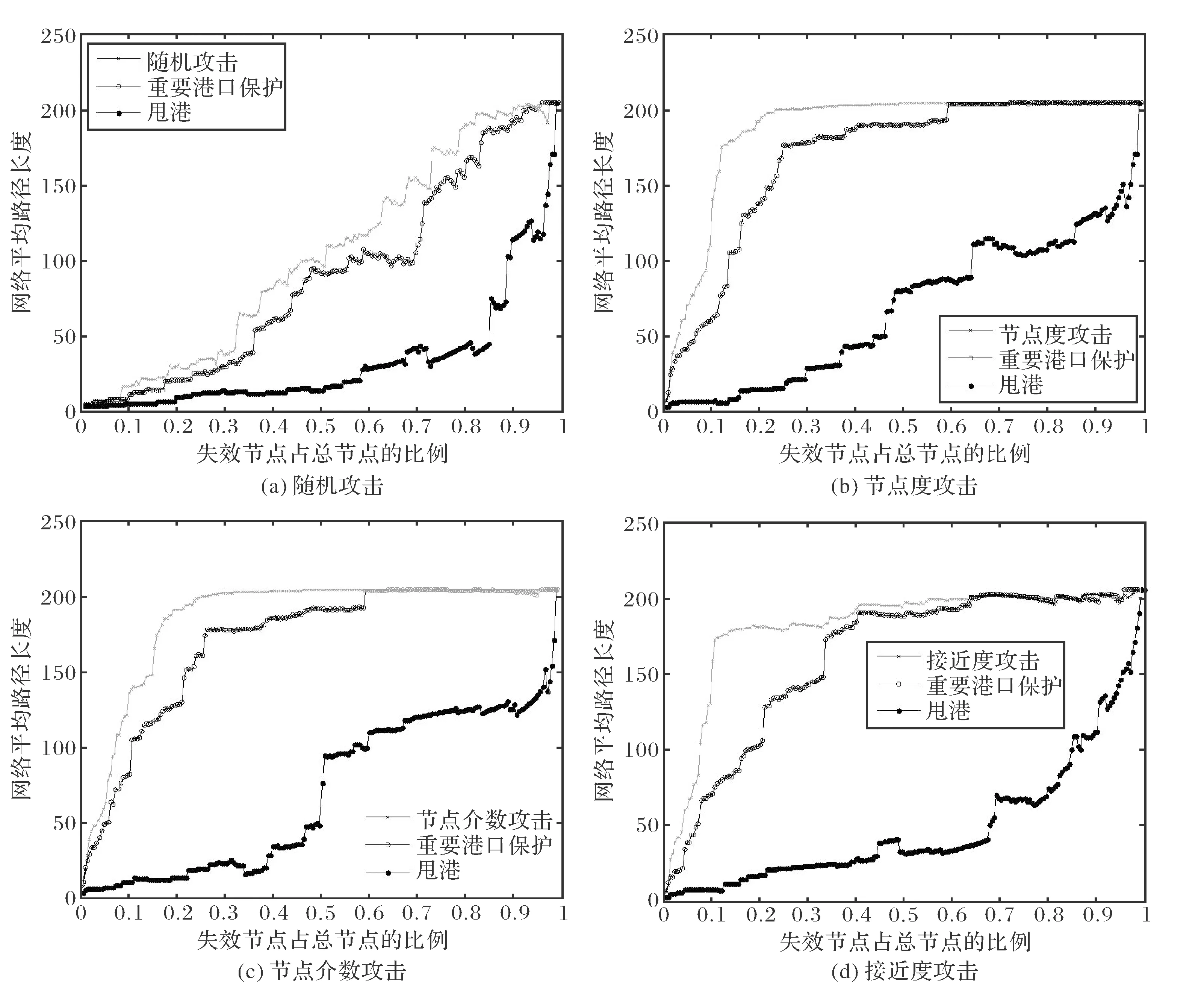
图5 不同应对策略下平均路径长度变化图Fig.5 Variation of average path length with different countermeasures

图7演示了不同应对策略下网络效率的变化，随机攻击下，没有采取策略和重要港口保护策略下的演化曲线是缓慢下降，而甩港策略下的演化曲线开始下降十分缓慢，等到删除90%的节点后，曲线迅速下降.通过以上分析可以看出，对于提高航线网络连通性来说，甩港策略的效果要更优于重要港口保护策略.

3.3 单个港口节点失效对网络连通性的影响

下面研究单个港口节点失效对海上丝绸之路航线网络性能的影响.对网络中的节点独立地依次进行攻击，表1为单个港口节点失效对网络的影响排名，排名越小说明该节点失效对网络连通性的影响越大.其中，Am表示网络平均路径长度；An表示甩港策略下网络的平均路径长度；ΔA表示平均路径长度下降的百分比；Sm表示网络最大连通子图的相对大小；Sn表示甩港策略下网络最大连通子图的相对大小；ΔS表示最大连通子图的相对大小上升的百分比；Nm表示网络效率；Nn表示甩港策略下的网络效率；ΔS表示网络效率上升的百分比.

表1 单个港口节点失效对网络平均路径长度的影响排名Tab.1 The impact on rankings of average network path length by attacking single port of network

表2 单个港口节点失效对网络最大连通子图的影响排名Tab.2 The impact on rankings of network maximal connected subgraph by attacking single port of network

表3 单个港口节点失效对网络效率的影响排名Tab.3 The impact on rankings of network efficiency by attacking single port of network

表4 测度相关性检验结果Tab.4 Test results of measurement correlation

由表1～表3可以看出，不同测度下，对网络连通性影响最大的前十港口排名并不相同，但就整体而言，3种测度下，这些港口多为东亚和东南亚地区的枢纽港，比如上海港、宁波港、新加坡港、迪拜港、丹戎不碌港等.为验证度、介数、接近度对网络连通性的评价性能，把表1中前10港口的排名与港口指标排名进行相关性分析得到相关系数及检验结果，如表4所示.从相关性分析结果可以看出，港口介数的评价结果均与3种连通性测度显著相关.表明节点的介数越大，该节点对网络连通性的影响就越大，因此，在对网络进行连通性优化时，可根据节点介数确定各个港口在网络中的重要性.

4 结论

本文基于复杂网络的相关理论，构建了海上丝绸之路航线网络，并对港口失效下的网络连通性及其应对策略进行了仿真研究.随机攻击下海上丝绸之路航线网络抵抗能力较强，而选择性攻击下抵抗能力较弱，尤其在初始度和初始介数攻击策略下，网络的连通性最差.不同攻击模式下，网络连通性测度变化都存在阈值，说明少数度值和介数较大的节点对网络连通性起着至关重要的作用，应当切实保障这类港口的正常、高效运行.同时，不同测度下，对网络连通性影响较大的港口多为介数较高的港口，多分布在东亚和东南亚地区，在对网络进行连通性优化时，可根据节点介数确定各个港口节点在网络中的重要性.

本文从拓扑结构角度研究了海上丝绸之路航线网络的连通性，丰富了现有的海上丝绸之路及航运网络理论，对网络设计与优化、网络可靠性分析与应急管理等起到借鉴作用.但部分内容仍不全面，没有考虑边失效对网络性能的影响，同时，网络连通性的优化策略有待于结合实际进行深入的研究，后续工作可从此进行展开.

[1] 曾庆成， 吴 凯， 滕 藤. 海上丝绸之路港口的空间分布特征研究[J]. 大连理工大学学报(社会科学版)， 2016，37(1)：25-31．

[2] 武佩剑. 集装箱班轮航运网络可靠性建模与仿真研究[D].大连:大连理工大学，2010．

[3] 楼春豪. 21世纪海上丝绸之路的风险与挑战[J].印度洋经济体研究， 2014(5)：4-16．

[4] 谭秀杰， 周茂荣. 21世纪海上丝绸之路贸易潜力及其影响因素[J].国际贸易问题， 2015(2)：3-12．

[5] 张 林， 刘霄龙. 异质性、外部性视角下21世纪海上丝绸之路的战略研究[J]. 国际贸易问题， 2015(3)：44-53．

[6] 赵 旭， 王晓伟， 周巧琳. 海上丝绸之路背景下港口战略联盟的稳定性研究[J]. 大连海事大学学报， 2016，42(2)：117-123．

[7] 曾庆成， 滕 藤. 海上丝绸之路航线网络的复杂性分析[J].中国航海， 2015，38(2)：122-126．

[8] BROUER B D， DESAULNIERS G， PISINGER D. A matheuristic for the liner shipping network design problem[J].Transportation Research Part E:Logistics and Transportation Review， 2014，72(C):42-59．

[9] JIANG J， LEE L H， CHEW E P， et al. Port connectivity study: an analysis framework from a global container liner shipping network perspective[J]. Transportation Research Part E: Logistics and Transportation Review， 2015，73:47-64．

[10] LIU D Y， WANG Z T. Thesis research on dynamic historical and geographic information system of Marintime Silk Road[C]//Proceedings of 2015 3rd International Conference on Social Science and Humanity(ICSSH 2015 V76). Surry: AER Proceedings, 2015.

[11] KUCHINS A C， SANDERSON T M， GORDON D A. Afghanistan: building the missing link in the Modern Silk Road[J]. The Washington Quarterly， 2010，33(2): 33-47．

[12] BULIS A， SKAPARS R. Development of “New Silk Road” northern branch through seaport of Riga in Latvia[J].Procedia-Social and Behavioral Sciences， 2014，150:1222-1229.

[13] CUI L T. Strengthening regional cooperation along the continental bridge and making a brilliant new silk road[J]. China Soft Science， 2001(10)：1-3．

[14] WATTS D J， STROGATZ S H. Collective dynamics of small world networks[J].Nature， 1998，393(6684):440-442．

[15] BARABASI A L， ALBERT R. Emergence of scaling in random networks[J]. Science， 1999，286(5439):509-512．

[16] BEATRIZ TOVAR， RUBÉN HEMNDEZ， et al. Container port competitiveness and connectivity: the Canary Islands main portscase[J]. Transport Policy， 2015，38:40-51.

[17] 程书恒. 基于鲁棒优化的集装箱海运网络模型研究[D]. 大连：大连理工大学， 2009．

[18] LI Z F， XU M Q， SHI Y L， et al. Centrality in global shipping network basing on worldwide shipping areas[J].Geojournal， 2015，80(1):47-60．

[19] 颜章龙. 世界海运网络拓扑结构及演化规律研究[D].大连：大连海事大学，2013．

[20] 宗 康， 胡志华. 基于复杂网络的海运航线网络连通性分析[J]. 大连海事大学学报， 2017，43(1):79-84．

[21] 赵亚龙. 基于复杂网络理论的煤炭运输网络抗毁性研究[D]. 北京：北京交通大学，2013.

[22] 汪 涛， 吴琳丽， 等. 基于复杂网络的城市公交网络抗毁性分析[J]. 计算机应用研究， 2010，27(11)：4084-4087．

[23] HOLME P， KIM B J， YOON C N， et al. Attack vulnerability of complex networks[J/OL]. Physical Review E， 2002，65(5)：1-15.[2002-05-07]. http://europepmc.org/abstract/med/12059649.DOI: 10.1103/PhysRevE.65.056109．

[24] 王松华. 基于异质网络的关键节点识别研究[D].重庆：西南大学，2014．

ResearchonconnectivitymodelingandsimulationforroutenetworkofMaritimeSilkRoad

YAN Nannan， LU Min， ZONG Kang

(Institute of Logistics Science & Engineering， Shanghai Maritime University， Shanghai 201306)

To promote the construction and optimization of Maritime Silk Road route network， the network connectivity is studied under different attack strategies and countermeasures from two views of local and global， which based on the related theory of complex network. The results show that the route network of Maritime Silk Road is robust under random attack and the connectivity is poor under selective attack. The countermeasures of skipping ports and protecting important ports is able to improve the network connectivity， and the effect under skipping measure is better than that under protecting measure. At the same time， the ports that have larger impact on network connectivity always be the ports with higher betweenness which located in East Asia and Southeast Asia， so betweenness can be used to determine the importance of ports when optimizing the network connectivity．

waterway transport; Maritime Silk Road; complex network; route network; connectivity

U697.1

A

2017-04-20.

国家自然科学基金项目 (71071093)．

*通讯联系人. E-mail: 406288747@qq.com．

10.19603/j.cnki.1000-1190.2017.05.017

1000-1190(2017)05-0655-08