硫排放控制区和碳减排约束下班轮航线优化

程文涛， 张华春

(上海海事大学 物流研究中心， 上海 201306)

硫排放控制区和碳减排约束下班轮航线优化

程文涛*， 张华春

(上海海事大学 物流研究中心， 上海 201306)

在航运市场运力过剩的形势下，为维持船公司的服务质量和满足环保要求，从船型选择，船舶数量，船速，碳税等方面建立硫排放控制区与碳减排下班轮航线成本模型，并通过lingo求解.选择某船公司位于“一带一路”沿线的亚欧航线进行实证分析.结果表明：在硫排放控制区背景下，班轮可通过减速最大限度的减少总成本，同时也会排放更多的CO2，综合考虑船公司采用区内区外航速不同是最佳的航行策略，船公司在下航期内低速航行，区外高速航行的策略将会实现经济效益与环境效益的平衡.对硫排放控制区的距离及碳税率进行灵敏度分析进一步验证区内区外航速不同为最优策略，可为船公司的决策提供参考.

硫排放控制区； 碳减排； 船速； 区内低速航行； 灵敏度分析； 航线优化

由于国际经济形势呈现出L型发展及周期性弱化特点以及船舶大型化的态势，航运市场的运力过剩问题仍然存在.与此同时，随着环境保护理念的深入人心，不受管制的船舶污染问题开始被各国所重视，纷纷开始制定政策与措施减少航运业的污染.如设立硫排放控制区等.面对如此形势，各船公司急需对已有的班轮航线航速进行优化.

针对航线航速优化问题，已有许多相关专家学者从不同方面对其进行研究：文献[1-4]从航线配船方面对其进行研究.邵俊岗[1]根据航运下行期运力过剩的现状，在现有配船模型基础上，建立混合整数规划模型，通过遗传算法求解.潘静静[2]建立双目标规划航线配船模型，使用Gurobi对模型求解.栾法敏[3]从减小经营成本入手，把原航线配船成本和新模型进行对比，发现优化后配船模型降低了经营成本.LIN[4]研究船公司在日班运作模式下的船舶路径和货运任务，建立整数规划模型，并通过拉格朗日松弛和本地搜索算法进行求解.文献[5-6]从航线网络优化方面进行研究.邓佳[5]根据沿海几大干线港口之间的运量需求，建立非线性规划与整数规划相结合的混合模型，选择典型航线建立运输网络，并对其进行优化.刘鲁凤[6]针对不确定环境下支线航运企业的班轮航线设计问题，以鲁棒优化为主要研究方法，建立了支线航运网络优化模型，并设计优化航线生成算法进行求解.文献[7-8]介绍了硫排放控制区的研究现状.孙化栋[7]介绍MARPOL73/78公约及相关法令对SO2排放的要求，阐述降低SO2排放的3种方法，并从各自优劣、应用前景等方面进行分析.CHANG等[8]假设韩国仁川港设立排放控制区域，对减速措施的效果以及燃油含硫量为 1%和0.1%两种规则进行研究.文献[9-10]研究了碳减排下的航线优化.叶德亮[9]在绿色低碳环保的大环境下，建立了班轮航线配船新模型，并在碳排放约束条件下进行了优化，并用lingo进行求解.LEE[10]通过环保型全球贸易分析模型定量分析征收航海碳税对经济的影响.SONG[11]利用船舶废气排放自动识别系统获取的实时数据，研究了上海洋山港的船舶排放清单和相关的社会成本. 文献[12-15]从船舶航速方面方面进行研究.高超峰[12]分析航行速度对船舶油耗产生的影响，建立混合整数规划模型.张燕[13]将航速作为变量，以总利润最大为目标，建立非线性混合整数规划模型，通过算例的计算及与其他方法的对比得到更优的航线网络.闫明胜等[14]对主机长期低转速运行对汽缸油影响及国际、国内排放法规实施对船用汽缸油性能要求进行分析，提出更换油品的解决方案.FAGERHOLT等[15]构建了在硫排放控制区域的班轮航线和速度优化模型，用以决定船舶航行的路线和速度，最大限度的减少船舶的运营成本.

本文在上述研究的基础上综合考虑硫排放控制区和碳减排，且同时考虑船型选择，船舶数量，船速，碳税等因素，设计硫排放控制区与碳减排下班轮航线成本模型，建立船速相同和船速不同的策略，并用lingo软件求解，选择最优策略.并对硫排放控制区距离和碳税进行灵敏度分析验证最优策略的可行性.以期实现经济效益与环保效益的完美结合，降低船舶的运输成本以及减少船舶废气的排放.

1 问题描述

当前虽然国际航运需求在短时间内继续保持温和增长态势，但运力的过剩的现象在相当长一段时间里仍然会存在.与此同时，船舶污染问题逐渐被人们所重视与关注，各国纷纷出台相关政策与措施来控制航运业的船舶污染.在这纷繁复杂的大环境下，如何兼顾企业的服务质量以及环保要求已经成为整个航运业急需面对的难题.

2 模型

2.1 模型假设

在当前硫排放控制区(Emission Control Area， ECA)与碳减排的背景下，考虑到船型选择，船舶数量，船速，碳税等因素的相互联系、相互影响、相互作用的关系，做出如下假设，见表1.

表1 模型假设Tab.1 Hypothesis of model

2.2 模型参数假设及关系计算

2.2.1 参数假设 为了对于后面方便计算，相关参数假设如下，见表2.

表2 相关参数假设Tab.2 Hypothesis of parameters

2.2.2 参数关系计算

1) 船舶循环航次时间T(h)

a) 船舶在排放控制区域(ECA)外的航行时间(h)

;

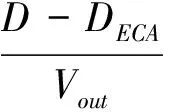
(1)

b) 船舶在排放控制区域(ECA)内的航行时间(h)

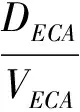
(2)

c) 船舶在港时间(h)

(3)

其中，ηi是在第i个港口的装卸量，它包括第j个港口的进口量(从别的港口运输至第i个港口的货物量)以及出口量(从第j个港口运输至其他港口的货物量)，可表示为

(4)

d) 船舶循环航次时间(h)

船舶循环航次时间(单次航程时间)是指在船舶航行过程中某一艘船舶在航线上完成一个航次的总时间，通常来讲，由在排放控制区域(ECA)内的航行时间、排放控制区域(ECA)外的航行时间、船舶在港口所花费的装卸时间以及船舶进出港口所花费的引航时间几个部分组成;

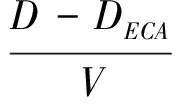
(5)

e) 航线上的配船数

为了保证航线周班的挂靠频率，也就是说，船舶发船间隔为一周.所以，一条航线上航次运营的船舶数量必须等于航次所用周时间，即n=W.故该航线上配载的船舶数为

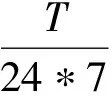
(6)

2)船期费Cs(USD/w)

(7)

3)进港费用成本Cp(USD/w)

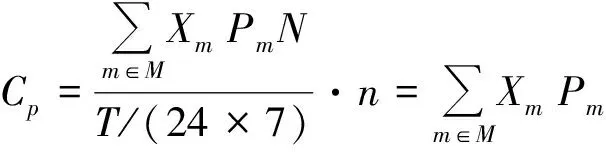
(8)

4)集装箱装卸成本CL(USD/w)

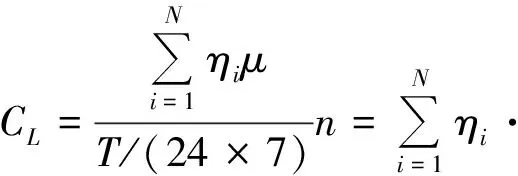
(9)

5)燃油成本CF(USD/w)

a) 船队平均每周主机HFO的消耗量(t/w)

将立方规则应用到燃油消耗中，得出船队平均每周主机HFO的消耗量为：

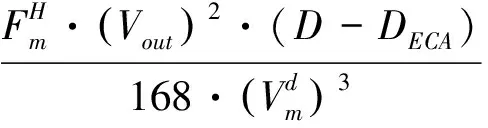
(10)

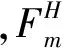
b) 船队平均每周主机MGO 的消耗量(t/w)

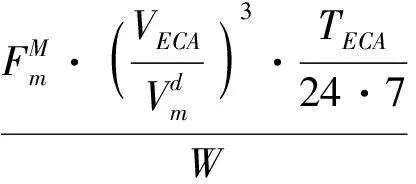
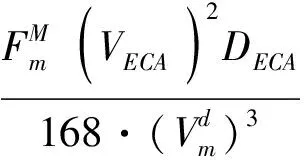
(11)

c) 船队平均每周辅机燃油的消耗量(t/w)

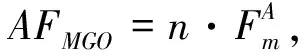
(12)

d) 船队平均每周的燃油成本(USD/w)

CF=MFHFOPHFO+MFMGOPMGO+AFMGOPMGO=

(13)

6)碳排放成本CCO2(t/w)

a) 船队平均每周的二氧化碳排放量(t/w)

航运CO2排放量取决于一定时期内船舶燃油消耗量和燃油的碳转换系数.船队平均每周的CO2排放量可表示为

ECO2=λHFOMFHFO+λMGO(MFMGO+AFMGO)=

(14)

b) 船队平均每周的碳排放成本(t/w)

CCO2=Ω·ECO2=Ω·[λHFOMFHFO+λMGO(MFMGO+AFMGO)]=

(15)

7)其他要素计算

各航段货物总量Yk(TEU).如图 1 所示，本文中第k个航段上的运输的货物总量为

(16)

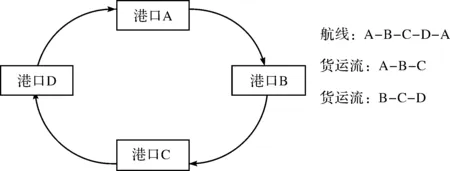
图1 货运流示意图Fig.1 Flow chat of freight transport

3 模型构建

在硫排放控制区与碳减排背景下，考虑硫排放控制区内、区外航速不同，其它条件不变建立航线优化模型如(17)、(18).

目标函数(17)表示硫排放控制区与碳减排下的班轮航线循环航次(每周)船舶总运输成本最小，由2部分组成，第1部分包括船舶每周的船期费、船舶每周的港口使费、船舶每周的装卸费用、船舶每周的燃油费用；第2部分是每周的碳排放成本.

式(18)为约束函数.其中，第1个约束条件与第2个约束条件表示航线上配置同一种类型的船舶；第3个约束条件是船舶容量限制，即船舶的运力始终可以满足航线上的货物运输的要求；第4个约束条件是船速限制，ECA内的船速不大于ECA外的船速，且ECA内外的船速必须在一定范围内；第5个约束条件是一条航线上航次运营的船舶数量必须等于航次所用周时间；第6个约束条件与第7个约束条件是非负以及整数约束.

minTC=Co+CCO2=CS+CP+CL+CF+CCO2=

(17)

(18)

为了研究硫排放控制区政策下，ECA内外速度变化是否对班轮运输的总成本有影响，我们研究ECA内外速度相同时，班轮航线总成本的情况.即将约束条件中的第4个约束变为公式(19)，接着与前面区内区外航行速度不同的情况进行对比，即得

(19)

4 结果与分析

上述建立的硫排放控制区与碳减排下班轮航线运输成本模型是混合整数非线性规划模型，其目标函数以及约束条件都具有非线性的特点，同时模型的变量包含整数变量和连续变量.可使用lingo求解相应的运输成本模型.

首先选择“一带一路”沿线的一条航线作为研究对象，采集相关数据与资料，并且利用lingo求解.将考虑两种不同情况下所建模型进行实例验证并进行对比，接着从碳税税率、ECA内的距离这两个方面进行灵敏度分析，验证区内区外航速不同的情况为最优策略的可行性.

4.1 数据采集

本文选择某船公司位于“一带一路”沿线的一条亚欧航线为研究对象，航线的航行距离全长22 507海里，硫排放控制区(SECA)内的距离为2 000海里.该航线按照一定的港口挂靠顺序进行航行.如图2所示，沿线的港口为：宁波港—盐田港—巴生港—吉达港—热那亚港—瓦伦西亚港—科伦坡港—釜山港—青岛港—宁波港.假设该船公司拥有的船型主要分为4种，不同船型的各项参数如表3.

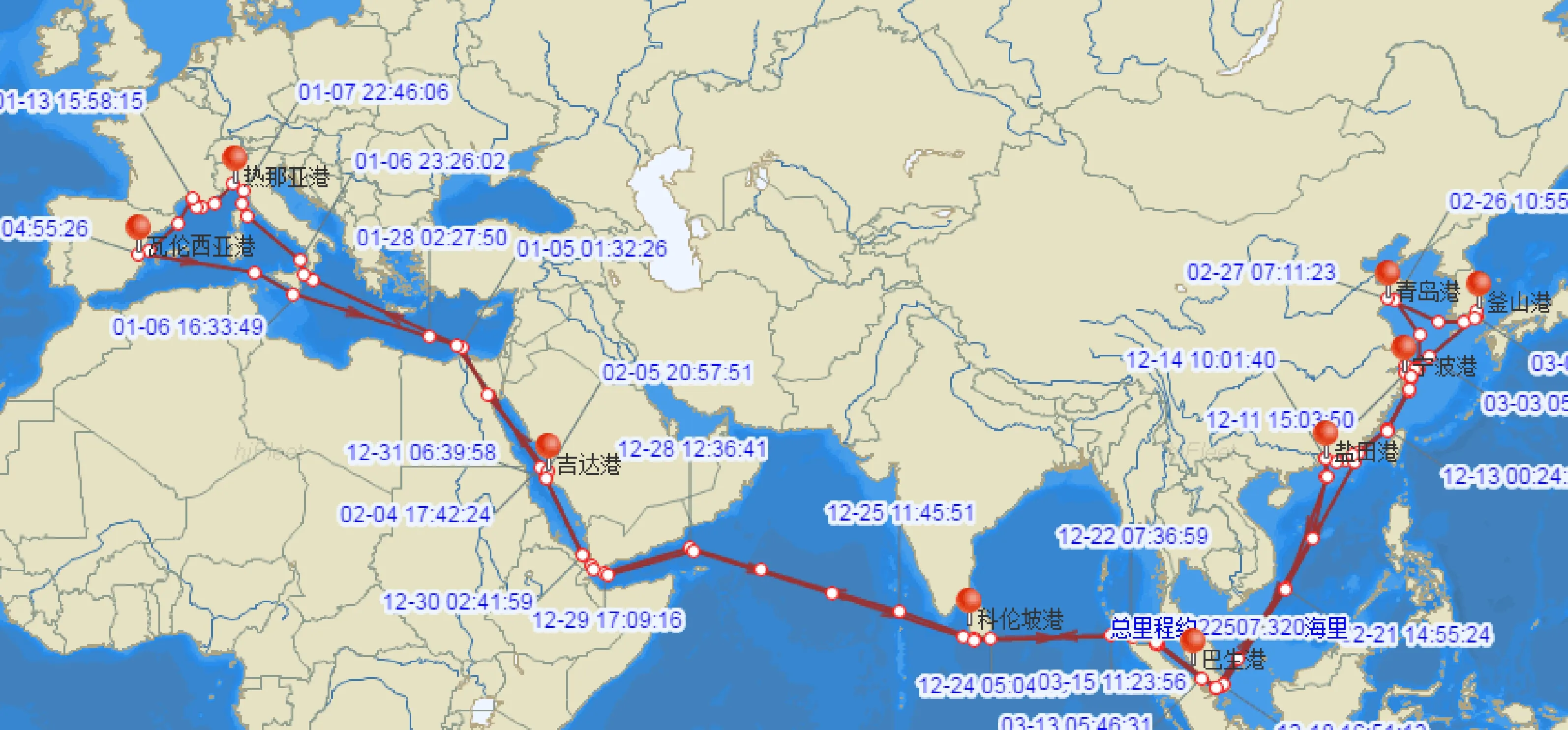
图2 某航线的港口挂靠情况Fig.2 Port affiliation of one shipping line

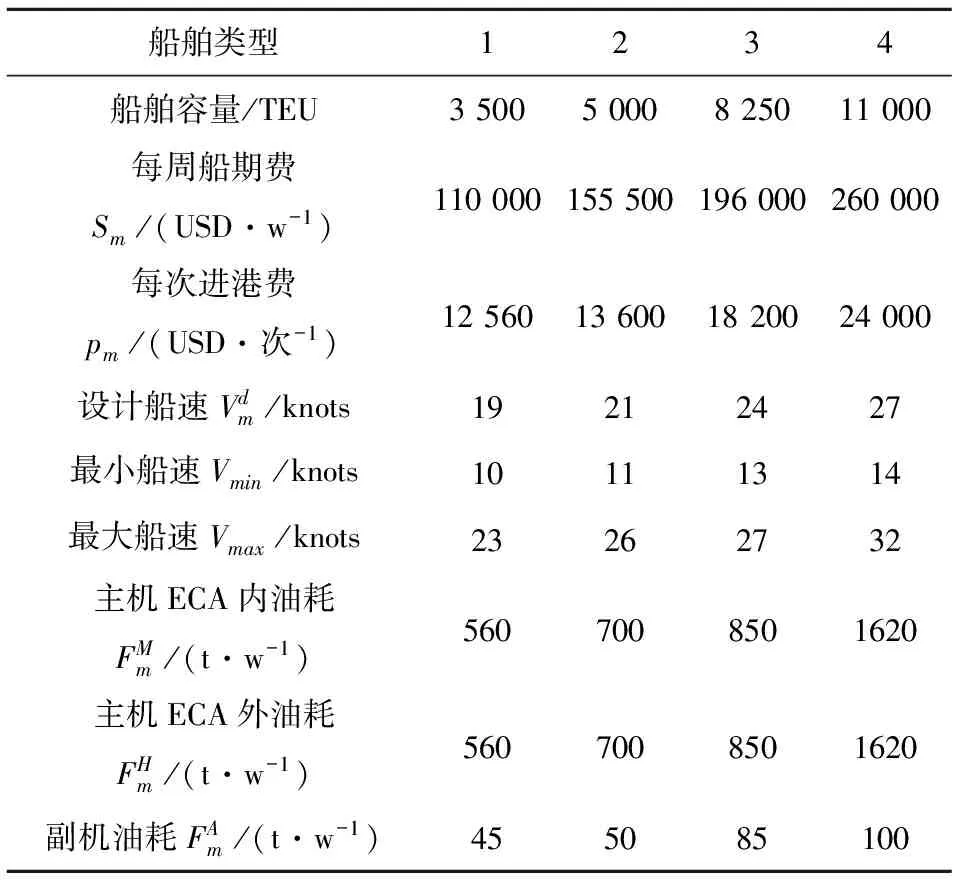
表3 船队相关参数

另外，通过MATLAB中的随机函数随机生成各挂靠港口间的货物需求情况，并满足[200，800]的均匀分布，如表4所示.模型中各参数的取值情况如表5所示.

表4 沿线挂靠港口间的货物需求情况Tab.4 Requirement of cargo in different ports along the shipping line

表5 部分参数取值情况表Tab.5 Value of several parameters

4.2 结果分析与比较

利用lingo软件编写相应代码对上述模型两种情况进行求解，得到的结果如表6所示.

从以上两种情形的优化结果，可以得出如下结论.

1) 由于通过MATLAB随机生成各港口间的货运量都是已知的，即各挂靠港口的货运量是固定的，所以每周的装卸成本一定，均为2 983 500 USD.

2) 由于各港口间的货运量如表4已知，并且考虑到船舶的最大装载能力必须大于每个航段上的货运量，所以本文选取装载能力为5 000TEU的船型来进行研究.与此同时，船舶每次的进港费用与船舶的大小有关，故船舶每周的进港费用都是240 000 USD.

3) 由于航速的不同，与航速相关的总成本、燃油成本、碳排放成本、碳排放量都有相应的变化.

4) 在排放控制区设立的前提下，区内与区外采用不同的航行速度.由上表可得，情形1的循环航次总成本最小，为 8 810 055 USD.与情形2的8 815 971美元相比，每周的循环航次成本少了0.067%.

5) 情形1与情形2相比，发现在区内与区外航速的因素下，结果存在很大差距.情形1在排放控制区设立的背景下，区内区外航速不同，使得情形1的燃油成本明显低于情形2的燃油成本，这表明在情形1中，区内船舶采用低速航行有利于减少燃油成本；与此同时，由于情形1在区内采用低速航行，为了满足运输效率，区外势必会加速航行，这势必会增加碳排放量，从而使得碳排放成本急剧上升.总之，在硫排放控制区的背景下，虽然船舶在进入 ECA 时使用高价的低硫燃油 MGO，但是却可以通过减速的办法最大限度的减少总成本.但是不容忽视的是，这样的做法会排放更多的CO2.

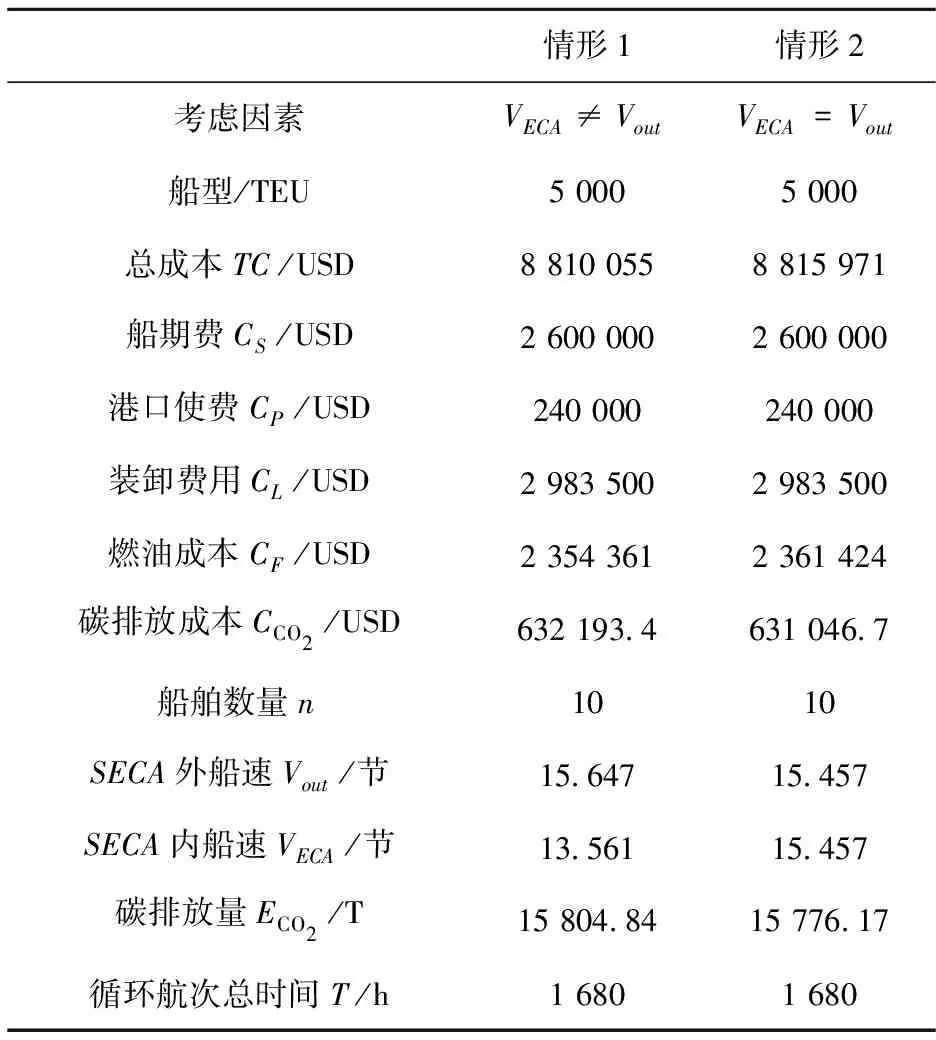
表6 不同情形下成本模型的情况Tab.6 The cost model under different circumstances

6) 总之，情形1、2相比，可以发现，船公司采用区内区外航速不同是最佳的航行策略，其次是匀速航行.

4.3 灵敏度分析

情形1(区内低速航行的策略)是各大船公司在航运业处于下行期的最优策略.下面为了进一步更加直观的了解排放控制区域距离、碳税税率对班轮运输成本的影响效果，进一步验证情形1为最优策略，将对上述影响因素进行灵敏度分析.

4.3.1 硫排放控制区距离 针对情形1中的排放控制区域距离从 1 000～2 600 海里进行分析，得出结果如表7及图3所示.

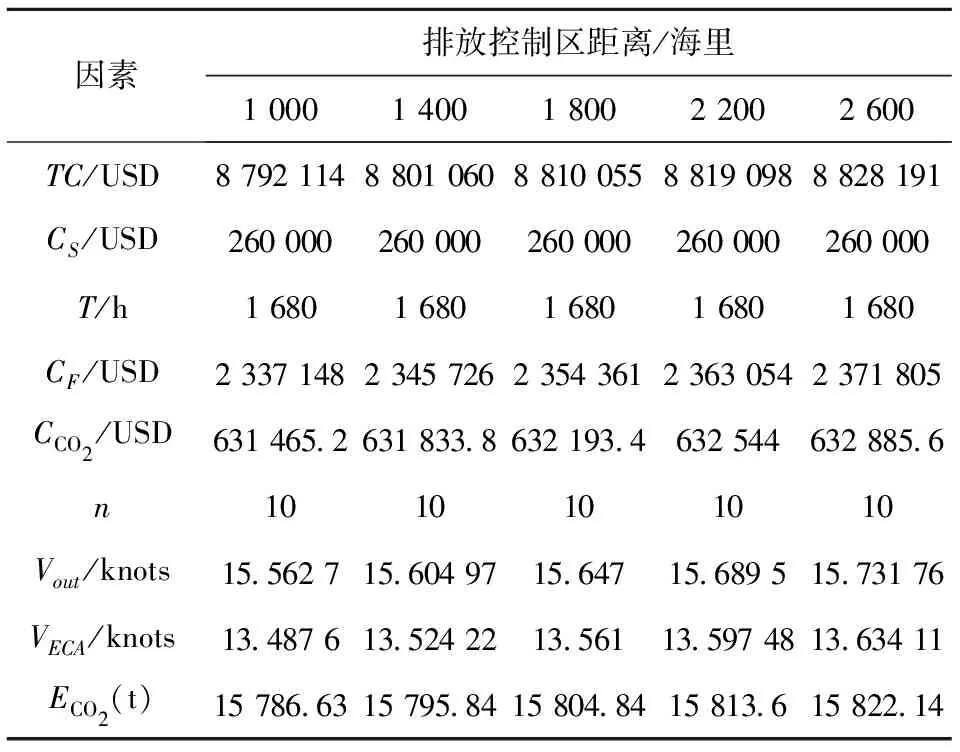
表7 排放控制区内距离灵敏度分析Tab.7 Sensitivity analysis of distance in the ECA

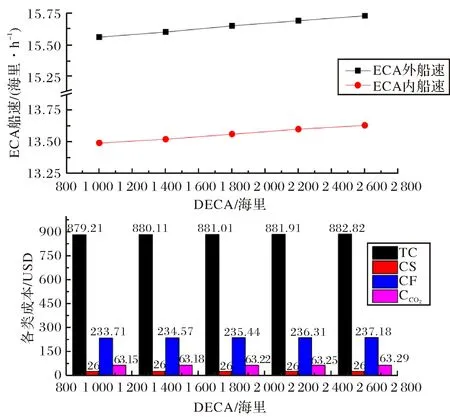
图3 排放控制区内距离灵敏度分析Fig.3 Sensitivity analysis of distance in the ECA

从表7 和图3可知.

1) 在硫排放控制区设立的背景下，随着排放控制区距离的增加，各船公司每周的循环航次总成本、燃油成本、碳排放量、碳排放成本呈现出上升的趋势；与此同时，ECA内外的航速基本保持不变，始终保持区内低速航行的策略.

2) 由于ECA距离直接决定并影响MGO的消耗量，所以当ECA距离增加时，将会消耗更多的MGO，燃油成本会显著增加.

3) 在硫排放控制区设立的背景下，ECA距离的增加，虽然可以有效的减少硫化物排放，但二氧化碳的排放量却会增加.

4.3.2 碳税征收系数 针对情形1中的碳税效率从20～60(USD/t)进行分析，得出结果如表8及图4，可以看出：1) 随着碳税税率的提高，船舶每周的碳税成本呈现出急剧上升的趋势，这使得循环航次的总成本也增加；2) 碳税税率的增加会使的船公司的碳排放量急剧下降，以期降低自身的碳排放成本.

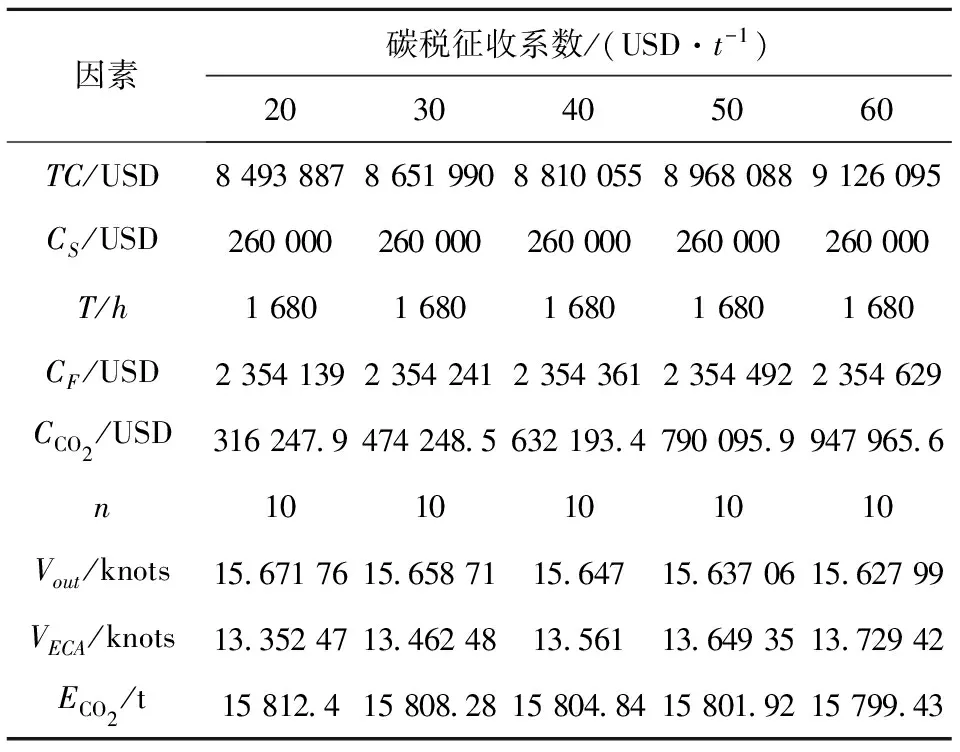
表8 碳税税率灵敏度分析Tab.8 Sensitivity analysis of Carbon tax rate

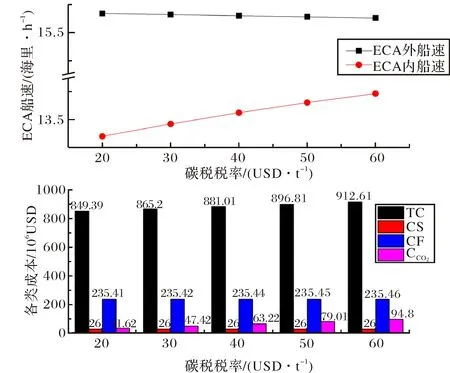
图4 碳税税率灵敏度分析Fig.4 Sensitivity analysis of Carbon tax rate

5 结语

本文在硫排放控制区和碳减排背景下，考虑硫排放控制区区内区外航速相同和航速不同2种情形，并考虑船型选择，船舶数量，船速，碳税等因素，建立了硫排放控制区与碳减排下班轮航线成本模型，并用lingo软件求解，求解结果表明：情形1为最优策略，能兼顾环保要求和成本要求.对硫排放控制区的距离及碳税率进行灵敏度分析进一步验证了情形1为最优策略，为船公司在复杂的变化多端的班轮市场中和愈发严格的政策下进行动态决策，在保证服务质量和符合政策要求的情况下最小化成本，保持市场竞争力提供参考.

[1] 邵俊岗， 薛颖霞. 航运下行期的航线配船和航次设计优化[J]. 上海海事大学学报， 2014，35(2):38-42．

[2] 潘静静. 基于双目标规划的班轮航线配船[J]. 重庆交通大学学报(自然科学版)， 2016，35(6):136-140．

[3] 栾法敏. 集装箱班轮航线配船模型的优化研究[D]. 青岛：中国海洋大学， 2009．

[4] LIN D Y， TSAI Y Y. The ship routing and freight assignment problem for daily frequency operation of maritime liner shipping[J]. Transportation Research Part E Logistics & Transportation Review， 2014，67(C):52-70．

[5] 邓 佳， 乐美龙. 沿海内贸集装箱班轮航线优化研究[J]. 中国水运:学术版，2007，7(11):21-22．

[6] 刘鲁凤. 区域集装箱航运支线网络优化研究[D]. 大连：大连海事大学， 2015．

[7] 孙化栋. 船舶硫氧化物的排放控制[J]. 世界海运，2012，35(8):51-54．

[8] CHANG Y T， ROH Y， PARK H. Assessing noxious gases of vessel operations in a potential Emission Control Area[J].Transportation Research Part D Transport & Environment， 2014，28(2):91-97．

[9] 叶德亮， 黄有方， 胡坚堃. 低碳模式下班轮航线配船问题研究[J].华中师范大学学报(自然科学版)，2015，15(4):199-203．

[10] LEE T C， CHANG Y T， LEE P T W. Economy-wide impact analysis of a carbon tax on international container shipping[J]. Transportation Research Part A Policy & Practice， 2013，58(4):87-102．

[11] SONG S. Ship emissions inventory， social cost and eco-efficiency in Shanghai Yangshan port[J]. Atmospheric Environment， 2014，82(1):288-297．

[12] 高超锋， 肖 玲， 胡志华. 考虑船舶油耗的集装箱班轮航线配船方案[J]. 华中师范大学学报(自然科学版)， 2014，48(6):840-846．

[13] 张 燕， 杨华龙， 计明军， 等. 考虑航速优化的班轮航线网络设计[J]. 交通运输系统工程与信息， 2016，16(5):219-226．

[14] 闫明胜. 主机长期低转速运行和硫排放控制对船用汽缸油的影响及对策[J]. 世界海运， 2017(1):37-40．

[15] FAGERHOLT K， GAUSEL N T， RAKKE J G， et al. Maritime routing and speed optimization with emission control areas[J]. Transportation Research Part C Emerging Technologies， 2015，52:57-73．

Sulfuremissionscontrolareaandcarbonemissionreductionunderthelinerrouteoptimizationresearch

CHENG Wentao， ZHANG Huachun

(Logistics Research Center， Shanghai Maritime University， Shanghai 201306)

In order to maintain the service quality of the shipping company and meet the environmental protection requirements， the cost model of the sulfur emission control zone and the carbon emission reduction liner line is established from the aspects of ship selection， ship number， ship speed and carbon tax. The above model is solved through lingo. The Eurasian route of a shipping company located in the area along “the Belt and Road” is chosen for empirical analysis. The results show that under the background of sulfur emission control area， the total liner cost is able to be reduced maximally by deceleration， while more CO2will be discharged. The best navigation strategy is to comprehensively consider the difference between the speed of the ship and the outside route. The strategy that ship company operates at low speed during the next voyage， while high speed at outside the area will realize the balance of economic benefits and environmental benefits. The sensitivity analysis of the distance between the sulfur emission control zone and the carbon tax rate further validates the different routes within the zone， which will provide references for the decision of the shipping company．

sulfur emission control areas; carbon emission reduction; ship speed; local low speed navigation; sensitivity analysis; route optimization

F550.74

A

2017-04-20.

国家自然科学基金项目(71471109，71101088)；高等学校博士学科点专项科研基金项目(20113121120002)；交通部应用基础研究基金项目(2015329810260)；上海曙光计划基金项目(13SG48)；上海市教委科研创新项目(14YZ100)．

*E-mail: 1147006351@qq.com．

10.19603/j.cnki.1000-1190.2017.05.018

1000-1190(2017)05-0663-08