2017年模拟考试中一道导数题的解法研究*

白亚军

甘肃省永昌县第一高级中学 (737200)

2017年模拟考试中一道导数题的解法研究*

白亚军

甘肃省永昌县第一高级中学 (737200)

一、试题呈现

已知函数f(x)=-2(x+a)lnx+x2-2ax-2a2+a，其中a>0．

(1)设g(x)是f(x)的导函数，讨论g(x)的单调性；

(2)证明：存在a∈(0,1)，使得f(x)≥0在区间(1,+∞)内恒成立，且f(x)=0在区间(1,+∞)内有唯一解．

分析:本题主要考查导数的运算、导数在研究函数中的应用、函数的零点等基础知识，考查推理论证能力、运算求解能力、创新意识，考查函数与方程、数形结合、分类与整合、化归与转化等数学思想．本题在阅卷过程中，发现学生有以下六方面的错误:

1.求导不熟，比如乘法法则、分式求导；

2.运算能力不强，对函数式乱变形、一元二次方程求根公式乱写、乱约分；

3.对参数的处理能力不够，分类讨论的思想还不到位；

4.研究函数时没有注意函数的定义域；

5.多个同类单调区间乱表达；

6.第二个小题基本没有做，入手较难．

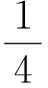
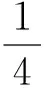
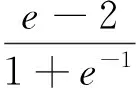
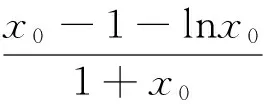
当a=a0时，有f′(x0)=0,f(x0)=0,由(Ⅰ)知，f′(x)在区间(1,+∞)上单调递增.故当x∈(1,x0)时，f′(x)<0，从而f(x)>f(x0)=0;当x∈(x0,+∞)时，f′(x)>0，从而f(x)>f(x0)=0.所以当x∈(1,+∞)时，f(x)≥0.

综上所述，存在a∈(0,1)，使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解．

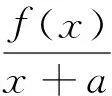
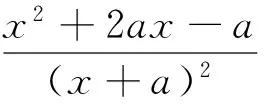
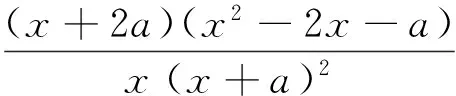
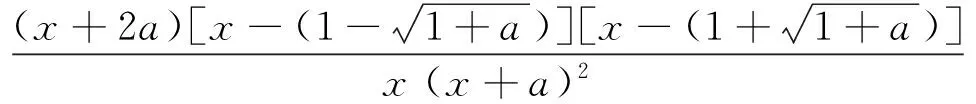
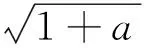
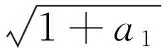
综上所述，存在a=a1∈(0,1)，使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解．

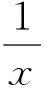
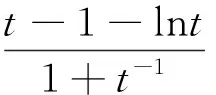
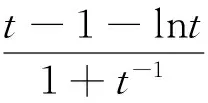
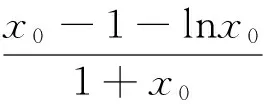
综上所述，∃a=a0∈(0,1)，使得f(x)的最小值为0．此时f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解．

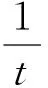
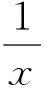
综上所述，∃a=a0∈(0,1)，使得f(x)的最小值为0．此时f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解．

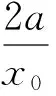
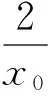
二、 教学建议

高考中的压轴题在素材选择、情景设置和设问方式上每年有所创新，基本都会考查二阶导数和分类讨论，考查学生的探究意识，应用意识和创新意识，对考生综合与灵活运用所学数学知识、思想方法，进行独立思考分析，创造性的解决问题有较高且合理的要求．

同时压轴题对数学思维的灵活性、深刻性、创造性都有较高要求，具有一定的难度，解答这些问题，需要具有较强的分析问题、探究问题和解决问题的能力．展示了数学学科的抽象性和严谨性，要求考生具有高层次的理性思维，考生解答时可以采用“联系几何直观—探索解题思路—提出合情猜想—构造辅助函数—结合估算精算—进行推理证明”的思路，整个解答过程与数学研究的过程基本一致，能较好地促进考生在数学学习的过程中掌握数学知识、探究数学问题和发现数学规律．这些试题具有立意深远、背景深刻、设问巧妙等特点，富含思维价值，体现了课程改革理念，是检测考生理性思维广度、深度和学习潜能的良好素材．这样的设计，对考生评价合理、科学，鼓励积极、主动、探究式的学习，有利于引导中学数学教学注重提高学生的思维能力、发展应用意识和创新意识，对全面深化课程改革、提高中学数学教学质量有十分积极的作用．

高考中的压轴题第1小问一般主要考查分类与整合的数学思想与方法．它是考试的必考点，同时也是学生解题的难点和易错点．就其原因，根本是没有想通为什么需要讨论，所以我们在平时的教学中，注意学生基本功的训练和过手，要经常进行不带参数和带参数的同一个问题的切换，让学生深深地体会到分类讨论是在“自然而然”中诞生的，而不是很勉强的，能避免则避免，有时是“无奈之举”.就此题而言，讨论“单调性”可化归为“解不等式”，最终是解“一元二次含参不等式”．走啊走，走到“Δ”这一关过不去了，非讨论不可，一切都是在自然而然中悄悄发生，高考中的压轴题第2小问是为优等生准备的“大餐”， 在处理时需要利用到主元转换(因式分解功底强大的则无需)，后续操作则只需注意变量的取值范围即可，此题需要考生强大的计算和心理承受能力，能明确自身目的所在，不至于在多重代换后迷失目标而功亏一篑．一般的学生是无福消受！所以在平时教学中对班上的优等生多加强一些思维训练，多给他们思考的时间、空间．针对这样的压轴题，要有心里准备，集中精力尽量去完成，争取多得分．

[1]张学忠,胡贵平.2016年全国高考导数题的几种解法[J].数理化学习,2016(8):29-30.

[1]陆丽.例谈不等式恒成立问题的解题策略[J].中学数学.2013(10):79-80.

*本文是甘肃省教育科学“十三五”规划课题《“三段六环”数学课堂教学有效性的研究》的研究成果，课题批准号GS[2016]GHB1348.