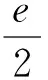对形如af 2(x)+bf(x)+c=0的题目探究

张小丹

四川省南充高级中学顺庆校区 (637000)

对形如af2(x)+bf(x)+c=0的题目探究

张小丹

四川省南充高级中学顺庆校区 (637000)

关于确定复合函数方程根的个数问题已成为近年高考的热点考题.本文将结合实例归纳出这类问题的求解方法,供学生们学习时参考.

例1 (2017吉林试验中学五模)

A.2B.3C.4D.5

分析：方程[f(x)]2-f(x)+a=0(a∈R)可视为关于f(x)的二次方程，所以不妨令f(x)=t，则[f(x)]2-f(x)+a=0(a∈R),即为t2-t+a=0与f(x)=t的复合.

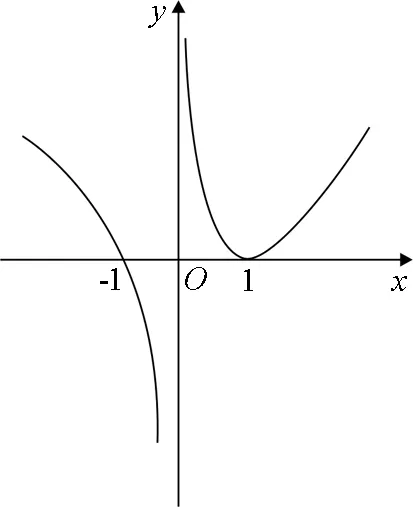
图1

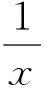
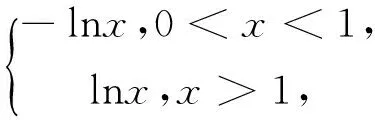
设f(x)=t，所以[f(x)]2-f(x)+a=0,即为t2-t+a=0.

观察图像易得(ⅰ)当t<0时，方程f(x)=t有一个根；(ⅱ)当t=0时，方程f(x)=t有两个根；(ⅲ)当t>0时，方程f(x)=t有三个根.

下面研究方程t2-t+a=0的根的个数.

1)当方程t2-t+a=0没有实根时，显然方程f(x)=t也无实根；

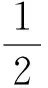
3)当方程t2-t+a=0有两不同根时，设这两个根为t1,t2，∵t1+t2=1，所以t1,t2不可能同时为负数，故方程f(x)=t不可能有两个根.故选A.

解题感悟：对于形如af2(x)+bf(x)+c=0的相关题目的解答，我们可以按照这样一个思路来进行：

(ⅰ)研究函数y=f(x)的图像或相关性质(如利用图像变换，解析式法，导数等工具研究)；

(ⅱ)根据(ⅰ)中y=f(x)的图像，研究关于x的方程f(x)=t的根的个数(对t的取值展开讨论)；

(ⅲ)根据题目条件以及(ⅱ)中讨论的若干情况，作出相应的结论.

例2 已知函数f(x)=

A.mn

D.m,n的大小不能确定

图2

分析：第一步，研究函数f(x)的大致图像当x≠1时，f(x)=|lg|x-1||，它可以由函数y=lgx的图像经过如下的变换方式得到：

y=lgx

第二步，研究x的方程f(x)=t的根.

观察图像易得(ⅰ)当t<0时，方程f(x)=t无根；(ⅱ)当t=0时，方程f(x)=t有三个根；(ⅲ)当t>0时，方程f(x)=t有四个根.

第三步，分析并作出相关结论.

设f(x)=t，则方程f2(x)+bf(x)+c=0,即为t2+bt+c=0.

由于方程f2(x)+bf(x)+c=0有7个不同的实数解，所以方程t2+bt+c=0必有两个根t1,t2，且其中一个根等于0，另一个根大于0，所以t1+t2=

-b>0⟹b<0，t1t2=c=0 ，所以b

分析：第一步，研究函数f(x)的大致图像.

图3 图4

第二步，研究x的方程f(x)=t的根.

设|f(x)|=t,t≥0，所以方程f2(x)+2a2=3a·|f(x)|，即为t2-3at+2a2=0.

对于方程|f(x)|=t,t≥0，观察|f(x)|的图像易得(ⅰ)当t≤0时，关于x的方程t=|f(x)|无解；(ⅱ)当0e时，关于x的方程t=|f(x)|有3个解.

第三步，分析并作出相关结论.

下面给出两个题目，供大家练习.

练习1 已知函数f(x)=|xex|，方程f2(x)-tf(x)+1=0(t∈R)有四个实数根，则t的取值范围为 ( ).

练习2 已知f(x)是定义在R上的偶函数，对于∀x∈R,都有f(2+x)+f(x)=0,当x∈[0,1]时，f(x)=-x2+1，若a[f(x)]2-bf(x)+3=0在[-1,5]上有五个根，则此五个根的和是( ).

A.7B.8C.10D.12

答案：A,C.