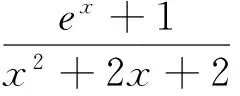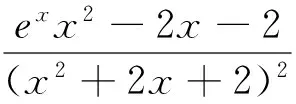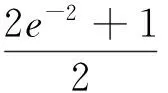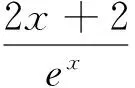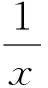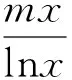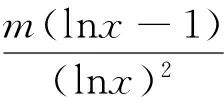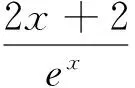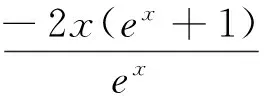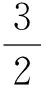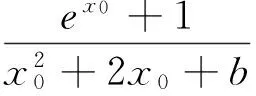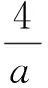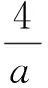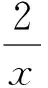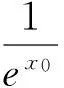从一道高考题的解答管窥函数的极值

王玉琴

甘肃省临泽一中 (734200)

从一道高考题的解答管窥函数的极值

王玉琴

甘肃省临泽一中 (734200)

题目(2016年山东高考数学文科题)设函数f(x)=xlnx-ax2+(2a-1)x，a∈R.

(1)令g(x)=f′(x)，求g(x)的单调区间；

(2)已知f(x)在x=1处取极大值，求实数a的取值范围.

(2)①当a≤0时，由(1)知f′(x)单调递增，所以当x∈(0,1)时，f′(x)<0，f(x)单调递减；当x∈(1,+∞)时，f′(x)>0，f(x)单调递增.因此f(x)在x=1处取极小值，不合题意.

1.解法探究

1．1 利用零点存在性定理

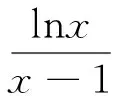
(2)当0<2a<1时，f(x)有两个不同极值点x1与1，且x1>1，由于f′(2a)=ln2a-4a2+2a<2a-1-4a2+2a=-(2a-1)2<0，故f(x)在x=1处取极小值，不合题意.

(3)当2a=0时，f′(x)=lnx，f(x)仅有一个极值点1，只因f′(2)>0，故f(x)在x=1处取极小值，不合题意.

(4)当2a=1时，f′(x)=lnx-x+1≤0，f(x)仅有一个极值点1，只因f′(2)>0，故f(x)在x=1处取极小值，不合题意.

1．2 利用导函数在极值点两侧的符号规律

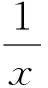
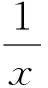
由此可得极值的如下性质.

2 性质

性质1 函数f(x)在定义域D内有极值⟺存在a,b∈D，使f′(a)·f′(b)<0.

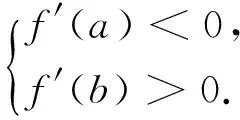
性质5 函数f(x)在定义域D内有唯一极值⟺y=f′(x)在定义域D内单调，且存在a,b∈D(a

(性质的证明非常容易，本文不再赘述)

3 应用

3．1 判定极值的存在性

因此函数F(x)有且仅有两个极值点.

3．2 判定极值的唯一性

例2 求证：函数f(x)=ex-lnx有且只有一个极值点.

故依函数极值的性质f(x)在(0,+∞)上有且只有一个极值点，且为极小值点.

3．3 求极值

当m>0时，f′(e2)>0，f′(2)<0，此时，f(x)仅有极小值f(e)=me，无极大值;

当m<0时，f′(e2)<0，f′(2)>0，此时，f(x)仅有极大值f(e)=me，无极小值.

3．4 比较大小

可知h(x)max=h(0)=2,从而b-2<2,即

3．5 证明不等式

分析:令h(x)=ag(x)-2f(x)=axex-

3．6 求解不等式恒成立

例6 已知不等式ex-ln(x+m)>0恒成立，求实数m的取值范围.

依函数极值的性质g(x)存在极小值点x0∈(-m,+∞),使g(x0)=(x0+m)ex0-1=0.则当x∈(-m,x0)时，g(x)<0，此时f′(x)<0，f(x)单调递减.当x∈(x0,+∞)时，g(x)>0，此时，f′(x)>0，f(x)单调递增.

可见，在判定函数极值存在性、唯一性、极值的大小，求极值，求与极值有关的参数取值范围及证明不等式的相关问题时，若能巧妙的利用函数极值的性质，定可优化思维，简化运算，巧妙解决问题.