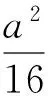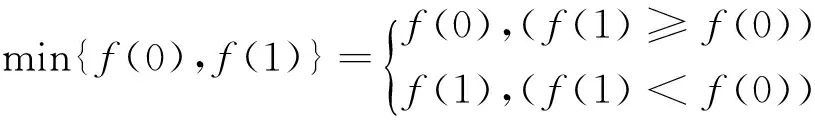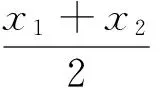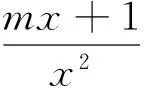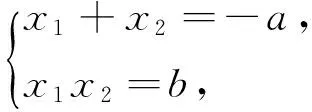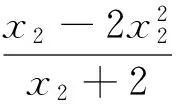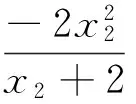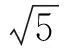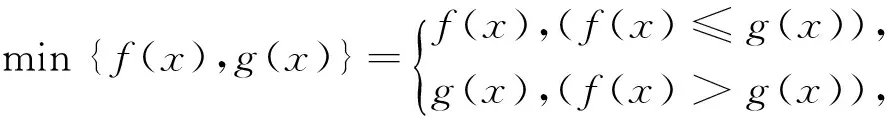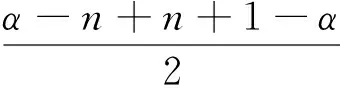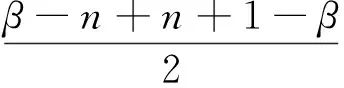利用函数零点式妙解一类函数题

严婷婷 陈少春

浙江省绍兴鲁迅中学 (312000)

利用函数零点式妙解一类函数题

严婷婷 陈少春

浙江省绍兴鲁迅中学 (312000)

函数是高中数学中一个非常重要的核心知识，二次函数作为众多函数里的“明星”备受考试命题者的青睐.最近浙江的模考卷、竞赛卷里频频出现一类函数问题，笔者发现如果用二次函数的零点式去处理，简洁明了，事半功倍.

例1 (2017年浙江高中数学竞赛题)设f(x)=x2+ax+b在[0,1]有两个实数根，则a2-2b的取值范围为_________.

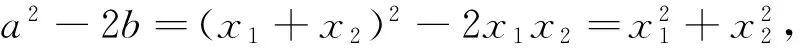
例2 (2014年浙江高中数学竞赛题)已知b,c∈R，二次函数f(x)=x2+bx+c在(0,1)上与x轴有两个不同的交点，求c2+(1+b)c的取值范围.

例3 (2017年浙江高考调测卷17题)已知函数f(x)=x2+ax+b在(0,1)有两个零点，3a+b的取值范围是_________.

解：设f(x)=x2+ax+b的两个零点为x1，x2，则0

例4 (2017年浙江模拟题)已知函数f(x)=ax2+bx+c(a>0)在(0,1)有两个零点，f(0)·f(1)是正整数，求实数a的最小值．

例7 (2015年浙江高考文数21题)设函数f(x)=x2+ax+b(a,b∈R)．

(2)若函数f(x)在[-1,1]上存在零点，0≤b-2a≤1，求b的取值范围.

解：(1)略；

-3≤b<0．

例8 (2011年北大保送生试题)设p、q为实数，函数f(x)=x2+px+q，如果f(f(x))=0只有一个实数根，求证：p，q≥0．

解：由题意知，f(x)=0必有实数根，设f(x)=(x-x1)(x-x2)，故f(f(x))=(f(x)-x1)(f(x)-x2)．下面用反证法证明x1≤0，x2≤0．不妨设x1>0，则由二次函数f(x)=x2+px+q开口向上及f(x)=0有实根知，方程f(x)-x1=0有两个不相等实根t1，t2，即f(x)-x1=(x-t1)(x-t2)，所以f(f(x))=(f(x)-x1)(f(x)-x2)=(x-t1)(x-t2)(f(x)-x2)至少有两个不相等的实根，与题设矛盾．从而p=-(x1+x2)≥0，q=x1x2≥0．