探析一道解析几何题的求解策略
2017-11-01虞懿
虞 懿
浙江省金华市第六中学 (321000)
探析一道解析几何题的求解策略
虞 懿
浙江省金华市第六中学 (321000)
解析几何的核心方法是用代数的方法研究图形的几何量(性质),核心思想是“数形结合”.2017年高考浙江卷第21题,保持了浙江卷背景熟悉、入口宽泛、解法多样的一贯风格,细细品读深感底蕴纯厚,紧扣解析几何的思想精髓.本文从解决解析几何问题的核心思想出发,着重探究本题第(Ⅱ)问的求解策略.
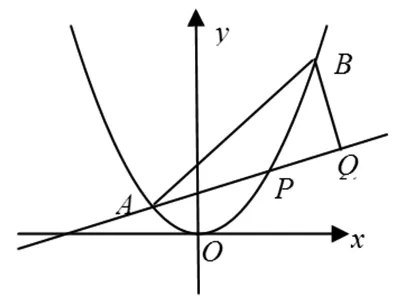
图1
一、试题展示

(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求|PA|·|PQ|的最大值.
品读:本题以抛物线为载体,主要考查抛物线的几何性质、直线与抛物线的位置关系、斜率与弦长等基础知识,同时考查解析几何的基本思想方法和综合解题能力.设计新颖,构思巧妙,耐人寻味,令人赏心悦目,体现了“能力立意”的指导思想,凸显了数学试题的选拔功能.
二、求解策略

(Ⅱ)策略1:选择恰当形式,实现几何量的代数表示
“几何量的代数表示”是解决解几问题的关键,在本题中的几何量是“|PA|·|PQ|”,用什么样的代数形式来表示这个几何量?对于弦长问题,很自然地联想到圆锥曲线的距离和弦长公式.而在解几中描述弦长的代数形式就是点或斜率,由此可想到用点坐标或斜率来表示几何量“|PA|·|PQ|”.
解法1:联立直线AP与BQ的方程
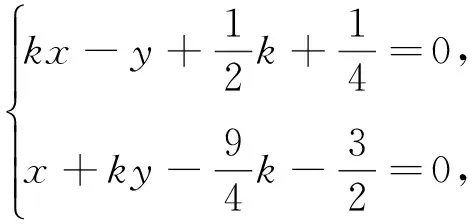


评析:联立两相交直线方程求出点Q的坐标,再根据两点间的距离公式,以斜率为参变量来表示弦长,建立目标函数.





评析:涉及弦长的问题,应熟练地利用根与系数的关系,通过设而不求计算弦长,以求达到简化运算的目的.
策略2:借助参数方程,实现几何量的代数表示

评析:利用直线的参数方程中参数的几何意义,避免了繁琐的计算,使得方程的联立简便易得.
策略3:回归向量知识本质,实现几何量的代数表示
向量具有代数、几何双重身份,融数形于一体,是沟通代数和几何的桥梁.它可以将几何问题坐标化、数量化,因此它是解决解析几何问题的重要工具.


评析:本解法构建平面向量,利用数量积的定义求|PA|·|PQ|,简洁明了.在探究解题思路时,要善于从不同的角度分析、挖掘它与其他知识的联系,在平面解析几何中有关长度、角度的计算及有关平行、三点共线、垂直等位置关系问题都可以用向量知识解决.
策略4:妙用极化恒等式,实现几何量的代数表示
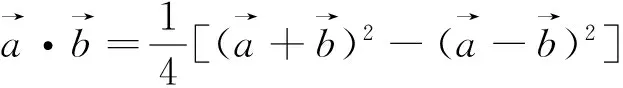


评析:极化恒等式的应用,由一般的直接运用到结合具体问题的巧用,需要学生恰当地运用转化思想,注意化动为定,特别是要结合题中的隐性特征进行转化处理,才能达到事半功倍的效果.
策略5:利用圆幂定理,实现几何量的代数表示
圆幂定理是平面几何中的一个定理,是相交弦定理、切割线定理及割线定理(切割线定理推论)的统一.例如,如果交点为P的两条相交直线与圆O相交于A、B与C、D,则PA·PB=PC·PD.

图2

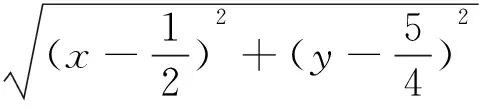
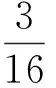
评析:巧妙利用圆幂定理进行转化,得|PA|·|PQ|=R2-|PC|2,避开求点Q的坐标,从而大大简化运算,并且后续化简也比较方便.
三、探究感悟
解析几何的核心方法是用代数的方法研究几何问题,在解题过程中,首先要将文字信息、图形条件进行转换,通过代数语言描述几何要素及其关系,将待求的几何量表示成代数式,然后进行适当的代数运算得出代数结果,最后通过分析代数结果的几何含义解决几何问题.在这个过程中要经历文字信息、图形特征和符号语言之间的多重转换,因此,我们必须重视对几何量(关系)的深入研究,探究用何种代数形式能恰当表示题目中的几何量(关系),同时有利于代数运算,从而形成正确的解题策略.
