初中生数学学习策略调查问卷的设计与编制

王光明，刘 丹



初中生数学学习策略调查问卷的设计与编制

王光明，刘 丹

（天津师范大学教师教育学院，天津 300387）

通过查阅文献资料与已有成熟问卷，征询专家意见，将初中生数学学习策略划分为三大维度：认知策略、元认知策略、资源管理策略，并确立了10个子维度的操作性定义．根据操作性定义，结合已有问卷，形成原始问卷．通过4次数据收集，经过多次项目分析、验证性因素分析、探索性因素分析，对问卷题目进行相应删减、增添、修改，最终形成“初中生数学学习策略调查问卷”．该问卷信效度指标良好，可作为测量初中生数学学习策略水平的有效工具．

初中；数学学习策略；问卷编制；量表

1 引 言

教育界将“教会学生学习，使学生掌握有效的学习策略”视为提高学习质量，减轻学习负担，大面积提高教学质量的有效措施．关于学习策略的研究，经历了从通用的学习策略到学科学习策略的发展过程，其中数学学习策略的研究受到了一定关注[1]．数学学习策略是高效率数学学习学生心理结构的重要组成部分[2]，有效的数学学习策略能够显著提高学生的数学学业水平，改善数学学习的态度和情感，对各学段学生的数学学习都存在积极影响[3~7]．数学学习策略对数学学习有着重要的作用，如何测量和评价学生的数学学习策略水平是相关量化研究中的重要环节．然而，目前针对中国初中生数学学习策略的测评工具尚十分罕见，研制科学规范的初中生数学学习策略调查问卷，成为亟待解决的问题．研究将参考已有数学学习策略问卷和量表，以初中生为研究对象，编制相应的数学学习策略调查问卷，为初中生数学学习策略特征的调查与量化研究提供有效的工具．

2 相关研究述评

2.1 数学学习策略成分的理论框架

学界对学习策略概念的界定众说纷纭，进而对学习策略结构的看法也不尽相同．具有代表性的分类有以下几种．

丹瑟路（Dansereau）根据学习策略所起的作用，将学习策略分为基础策略和支持策略两类．基础策略是指直接操作材料的各种学习策略，主要包括信息的获得、贮存，信息的检索和应用的策略，如识记、组织和回忆等策略．支持策略主要指帮助学习者维持适当的学习心理状态，以保证基础策略有效操作的策略，如集中注意策略、自我监控和诊断策略[8]．温斯坦（Weinstein）认为学习策略包括认知信息加工策略，如精加工策略等；积极学习策略，如应试策略等；辅助性策略，如处理焦虑的策略；元认知策略，如监控新信息的获得策略[9]．迈克卡（Mckeachie）等人根据学习策略覆盖的成分，将其概括为认知策略、元认知策略、资源管理策略．认知策略包含复述策略、精加工策略和组织策略；元认知策略包含计划策略、监控策略、调节策略；资源管理策略包含时间管理策略、学习环境管理策略、努力管理和其他人的支持[10]．

参考国外的学习策略调查问卷，中国研究者也编制了一系列数学学习策略调查问卷．譬如，刘电芝编制的“小学生数学学习策略量表”，该量表包含两个主要维度，数学元认知策略（计划策略、监控调节策略、评价反思策略、策略意识）与数学认知策略（数学概念策略、计算学习策略、解应用题策略、几何知识学习策略）[11]．姚志敏编制的“中学生数学学习策略量表”，包含数学元认知策略、认知策略、资源管理策略和情感策略4个维度[12]．王光明编制的“高中生数学学习策略调查问卷”，将数学学习策略划分为数学认知策略、数学元认知策略和数学资源管理策略[13]．

国外研究者对于学习策略的结构划分，具有一定的相似性．丹瑟路和温斯坦对学习策略结构的划分，多数可归类到认知策略、元认知策略和资源管理策略中，即迈克卡等人关于学习策略的分类．国内研究者在进行数学学习策略的维度分类时，也基本符合这一观点，分为数学认知策略、数学元认知策略和数学资源管理策略3类[14]．

2.2 数学学习策略问卷的相关研究

学习策略研究的基本问题之一，在于如何编制有效调查工具测评学生的学习策略水平．已有的各类学习策略调查问卷各有其优势所在，但也有不足．如温斯坦等人编制的“学习策略量表”（，）[15]，该量表最初为大学版，后改编为高中版；美国密执安大学宾特利奇（Pintrich）等人编制的学习动机与策略问卷（，）[16]，包含动机和学习策略两部分，该量表有大学版和中学版，尽管这两个版本的学习策略调查问卷都不涉及具体学科，但却都被研究者直接用于测验学生在数学学习中的策略使用情况．

目前已有的一些学习策略测量工具，鲜有专门针对初中生而设计，与数学学科的结合也并不紧密，甚至部分测量工具的编制过程也不够严谨．具体表现为两大类问题：第一，问卷的编写表述不明确，包括指导语表述不明确，以及测试题目表述不明确．第二，通过各类指标参数修订问卷的过程不规范．针对第一类问题，编写指导语时应明确题目中各个选项的定义，如在李克特量表中，就应清晰地告知作答者各等级选项的具体标准，尽可能地保证测验的科学性．测试题目表述不明确，主要包括程度副词的使用，以及模棱两可的词汇．譬如，测试题目“数学考试之前，我通常会根据自己的实际情况，有针对地复习一下”中，不同作答者对于“通常”的理解便可能存在偏差，应尽量避免使用此类语言．针对第二类问题，在问卷试题修订过程中，利用统计软件运算得到的各参数指标可以作为删减题目的依据，但不能将其作为删减题目的唯一依据，还需要考虑保留题目的语义是否清晰精简、是否覆盖所有维度等问题；进行因素分析时，探索性因素分析和验证性因素分析要使用不同的样本，进行验证性因素分析时要注意在分析过程中重新取样的问题．

3 问卷编制过程与方法

3.1 问卷维度及其操作性定义的确定

“初中生数学学习策略调查问卷”的维度确定主要包含两个步骤：（1）查阅文献资料与已有成熟问卷，拟定问卷维度及其操作性定义；（2）征询专家意见，确定问卷维度及其操作性定义．

首先，通过查阅梳理文献，以及已有的国内外成熟（数学）学习策略问卷，拟将初中生数学学习策略划分为三大维度（数学认知策略、数学元认知策略和数学资源管理策略），并编写各子维度的操作性定义．

其次，于2016年3—9月期间，分别对多位知名专家学者进行访谈，包括北京师范大学曹一鸣教授，南京师范大学喻平教授，天津师范大学李洪玉教授，佛罗里达海湾大学张京顺博士等，访谈内容包括问卷维度的具体划分及子维度操作性定义的具体界定．

综合文献资料、已有成熟问卷或量表，以及专家意见，最终确定问卷的维度，其中包括3个主维度，10个子维度．数学学习策略的维度划分见图1，各子维度的操作性定义见表1．

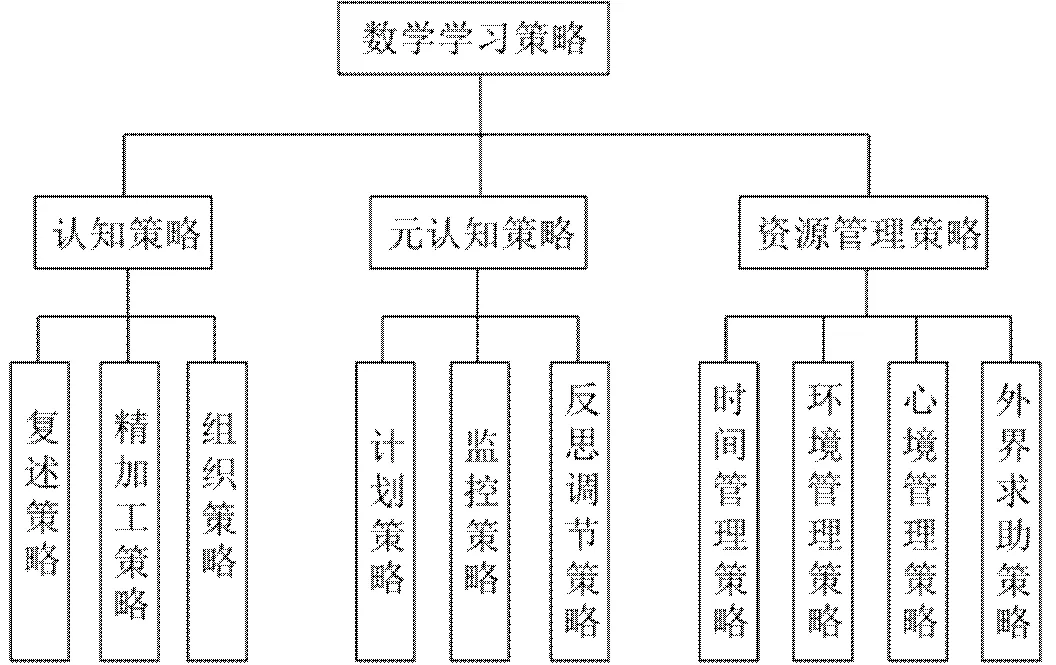
图1 数学学习策略的维度划分

表1 数学学习策略子维度的操作性定义

3.2 问卷题目的建立

所编初始问卷的题目主要来自于：（1）温斯坦的“学习策略问卷”（LASSI）[15]；（2）王光明的“高中生数学学习策略调查问卷”[13]；（3）莫秀锋的“数学学习策略量表”[1]．

考虑中国初中生数学学习的特点，引用和改编上述问卷的题目内容，建立了87道题目的问卷，其中认知策略26道，元认知策略28道，资源管理策略27道，测谎题6道．问卷采用likert五点法计分，将题目选项中的“非常符合”、“符合”、“不确定”、“不符合”、“非常不符合”分别计分为“5”、“4”、“3”、“2”、“1”．采用随机法编排题目顺序．

3.3 被试选取与问卷回收

问卷编制过程中，采用整群抽样法共进行4次测试．对于每次测试回收的问卷，通过以下两个步骤剔除无效问卷．第一步：目测，剔除问卷答案呈现规律性、周期性、统一性的无效问卷；第二步：根据测谎题对剩余的问卷继续进行筛选，凡是对测谎题回答差异性过大的均作为无效问卷剔除．

首次测试调查对象为预测试样本．包括天津市的4所典型学校共8个班级的学生，分别是实验中学、方舟实验中学、海河中学、天津五中的七年级和八年级学生．总共发放问卷330份，回收286份，通过两步问卷筛选，最终得到有效问卷209份．

第二次所测样本，主要用于问卷研制过程中的探索性因子分析．调查对象来自天津、湖北、辽宁、甘肃、江苏的5所中学．总共发放问卷610份，回收552份问卷，通过两步问卷筛选，最终得到有效问卷428份．

第三次所测样本，主要用于问卷研制过程中的验证性因子分析．调查对象来自天津、山东、广州的3所学校．总共发放问卷300份，回收264份问卷，通过两步问卷筛选，最终得到有效问卷209份．

第四次所测样本，主要用于计算问卷的重测信度．选取了参与过第二次测试的两所中学学生．共发放问卷160份，回收问卷142份，通过两步问卷筛选，最终得到有效问卷113份．

3.4 数据分析工具

利用SPSS18.0和AMOS21.0软件处理和分析问卷各参数指标．

4 问卷的预研究结果与分析

4.1 项目分析

对反向计分题进行反向计分后，按两个步骤对问卷的81道题目（不包括测谎题目）进行项目分析：首先，利用题总相关法对首次测试中所有被试的各题目得分与整卷总得分进行相关分析．一般情况下，当Pearson积差相关系数值低于0.4时，可认为二者之间存在低度相关．在0.05的显著性水平下，共计删除各题项得分与总分的Pearson积差相关系数低于0.4的题目13道．其次，采用临界比率法（Critical Ratio）进行高低分组的差异显著性进行检验，将数学学习策略得分按升序排序，前27%为低分组，后27%为高分组，对两组进行独立样本检验，删除不具有高低分组显著性差异的题目．结果显示，通过题总相关法删除题目后，剩余题目均满足高低分组间的差异显著性．经过项目分析，最终得到道68题目（不包括测谎题）．

4.2 探索性因素分析

将修订后的问卷进行第二次测试，利用所得数据先后对问卷整体以及3个主维度进行探索性因素分析．4次探索性因素分析前，所进行的检验值均达到0.9以上，Bartlett球形检验相关性显著（），说明样本数据适合进行探索性因素分析．

在SPSS软件中使用主成分分析以及最大方差旋转法确定问卷因子数及题目．保留问卷中的题目遵循如下原则：（1）因子特征值大于1；（2）因子载荷值至少在0.4以上；（3）在不同因子上载荷量不能均大于0.4；（4）提取出的主成分符合陡阶检验；（5）每个因子至少包含3道题目；（6）一次只删除一道题目，每一次删除题目之后用新的数据重新检验和分析．因子命名的原则如下：（1）如果某个因子的题目主要来自数学学习策略模型的某个子维度，则以该子维度命名；（2）如果对某个因子方差贡献率一半以上的题目分散来自于数学学习策略模型的不同子维度，则参考这些题目的共同数学学习策略进行命名．

通过探索性因素分析，共删除18道题目，保留了“数学学习策略调查问卷（第一版）”中的37道题目．尽管各类指标可以作为筛选题目的依据，但是不能仅依靠指标筛选题目，还需要考虑保留题目的语义是否清晰精简、维度划分的实际意义、因题量过多导致学生的作答专注度不高等问题．考虑到上述原因，需要对原维度进行合并或拆分，并重新命名．又结合学生答题过程中对第一版问卷中的部分题目的反馈，对部分题目的表述方式进行了修订．再将题目交叉混合编排，得到修改后的第二版问卷，共含46道题目（包括42道正式题目和4道测谎题），其中认知策略采用三因素结构，复述策略共5题，精加工策略共4题，组织策略共5题；元认知策略采用三因素结构，计划策略共6题，监控策略共6题，反思调节策略共4题；资源管理策略采用四因素结构，时间管理策略共3题，环境管理策略共3题，心境管理策略共3题，外界求助策略共3题．

5 问卷的正式确定及结果分析

为进一步修订和完善数学学习策略问卷，对第二次与第三次所测的样本进行再测问卷的调查．对回收问卷数据进行处理，通过项目分析和因素分析，对问卷的理论调查模型进行检验和调整．

5.1 项目分析与探索性因素分析

使用第二版问卷对第二次调查样本进行分析．先进行高低分组显著性差异的检验和题总相关性的分析后，删除第15题和第17题，剩余44道题目．再对数据进行探索因素分析，结果表明问卷因子确定合理，与理论框架基本吻合，进而确定第三版问卷．

5.2 验证性因素分析

使用第三版问卷对第三次测试样本进行调查，利用AMOS 21.0软件对数据进行验证性因素分析，以此检验实际测量结果与理论模型拟合效果是否良好．在对二阶3因子模型进行拟合前，先建立一阶10因子模型，再次筛选题项．通过分析一阶10因子模型的各主要参数指标，删除因子载荷值小于0.5的题目（第4、5、10、12、31、34题），剩余34道题．其次，通过观察修正指数，发现有两对题目之间的值在20以上，表明题目之间的相关性过高，删除第6、33题．

5.3 问卷的信度和效度指标

5.3.1 信度分析

信度是指测试结果的一致性、稳定性和可靠性，信度系数愈高，表示测试的结果愈一致、稳定和可靠．通过计算问卷的内部一致性和重测信度分析问卷的信度．数据分析结果（见表3）表明，初中生数学学习策略调查问卷的各主维度Cronbach’s系数在0.839~0.888之间，Spearman-Brown分半信度在0.768~0.856之间，说明编制的数学学习策略调查问卷各主维度内部题目的一致性程度很高．总问卷的Cronbach’s系数为0.970，Spearman-Brown分半信度为0.937，表明编制的数学学习策略调查问卷具有较好的内部一致性．重测时选取第四次测试样本，采用Pearson积差相关系数作为问卷的重测信度，分析两次测试分数的相关性．结果表明，问卷各主维度的重测信度在0.858~0.891之间，总问卷的重测信度为0.906．由此可知，问卷具有很好的内部一致性．结合各项信度指标，认为“初中生数学学习策略调查问卷”信度较高．

表2 二阶3因子模型拟合指数

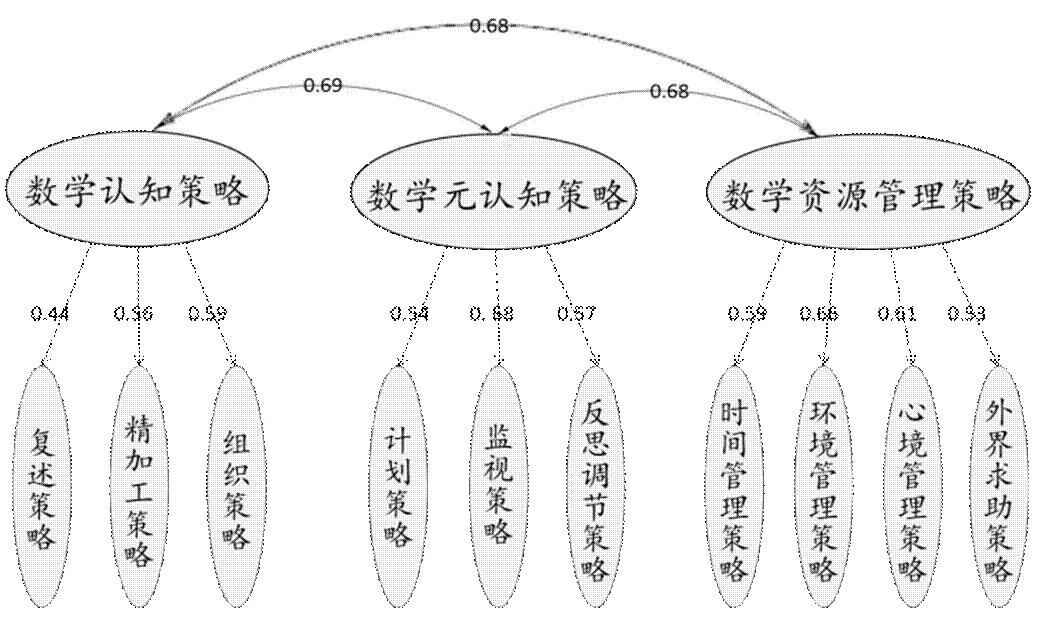
图2 初中生数学学习策略结构路径系数

表3 数学学习策略特征问卷信度

5.3.2 效度分析

效度即有效性，是指测量工具能够测出所需测量的内容的程度，效度越高，说明测量结果与要考察的内容越吻合；反之，则二者吻合度越低．通过分析问卷的内容效度和结构效度，以考察所编制问卷对于初中生数学学习策略特征测量的有效性．

（1）内容效度．

内容效度是指问卷题目反应所要测量的内容能否达到测量目的的程度．在形成初测问卷之前，题目内容借鉴了国内外已有量表或问卷，并考虑中国初中生数学学习的实际情况；之后又曾与多位专家进行讨论，讨论包括问卷的指导语编写、问卷的结构和题目编写的注意事项等内容，根据专家的意见对问卷中存在问题的题目进行修改或删除，构建调查模型，确定“初中生数学学习策略调查问卷”的题目．

在最终版本问卷内容效度的评价阶段，邀请了北京师范大学曹一鸣教授、南京师范大学喻平教授、天津师范大学李洪玉教授和王晓庄教授4位心理学或数学教育领域的专家，对问卷中每一题目与其所属维度的相关性做出评价，根据专家评价结果计算问卷的内容效度．结果表明，4位评价者间的一致性水平为0.84，表明评价者间具有较好的一致性．问卷条目水平的内容效度指数见表4．

表4 内容效度指标

（2）结构效度．

以验证性因素分析所显示的二阶模型拟合指标作为结构效度的指标之二．上文分析中，调查数据对模型的拟合已达到标准要求，认为“初中生数学学习策略调查问卷”的一阶10因子二阶3因子结构模型可以接受．

6 讨 论

自制的“初中生数学学习策略调查问卷”与“高中生数学学习策略调查问卷”[13]的编制过程既有相同，也有不同之处．继承了“高中生数学学习策略调查问卷”中对于数学学习策略维度的划分，“初中生数学学习策略调查问卷”也将数学学习策略分为数学认知策略、数学元认知策略和数学资源管理策略3个维度．不同之处体现在以下3个方面．

（1）题目数量和内容．“初中生数学学习策略调查问卷”包含的题目数量少于“高中生数学学习策略调查问卷”中题目数量，问卷题目的内容符合初中生数学学习的特点．精简问卷题目数量，避免学生由于答题时间过长而注意力分散，进而造成收集数据失真的情况，保证了所收集数据的真实性．

（2）题目和指导语的表述．“高中生数学学习策略调查问卷”题目表述中出现了“很少”、“常常”等这样表示频率的词语，例如，“我很少在实际生活中用到所学习的数学知识”，“我常常总结一些代表性的例题和解题方法”，这样的题目表述不是很清晰，易引起歧义．“初中生数学学习策略调查问卷”的编制过程中，为明确测试题目，题目的表达方式避免使用表示频率的词语，在指导语中增加了题目各个等级选项的定义．

（3）问卷的验证性因素分析．运用因素分析修订问卷的过程中，“高中生数学学习策略调查问卷”的验证性因素分析和探索性因素分析使用了同一样本数据，这种做法值得商榷．用于探索性因素分析时选用的样本数据进行验证性因素分析以支持自己的结论，这种“自圆其说”的做法是不可取的[17]．“初中生数学学习策略调查问卷”的编制过程中，为更好地检验问卷的各个题目与构想的理论模型是否具有良好的拟合效果，采用与探索性因素分析时不同的样本数据进行验证性因素分析．

问卷的编制，通过文献的梳理，结合专家意见，初步建构了数学学习策略调查问卷模型，形成第一版问卷，经多次测试与修订，分别得到第二、三、四版问卷．在四版测试数据的基础上，对调查模型进行修订，确立调查问卷的结构模型．“初中生数学学习策略水平调查问卷”共包含36道题目，分为3个维度和测谎题构成，具体题目分布见表5．

“初中生数学学习策略调查问卷”具有较好的信度和效度．该问卷具有扎实的理论基础，合理的结构框架．但由于各方面的限制，问卷的编制尚未制定全国常模，这是进一步研究的方向．

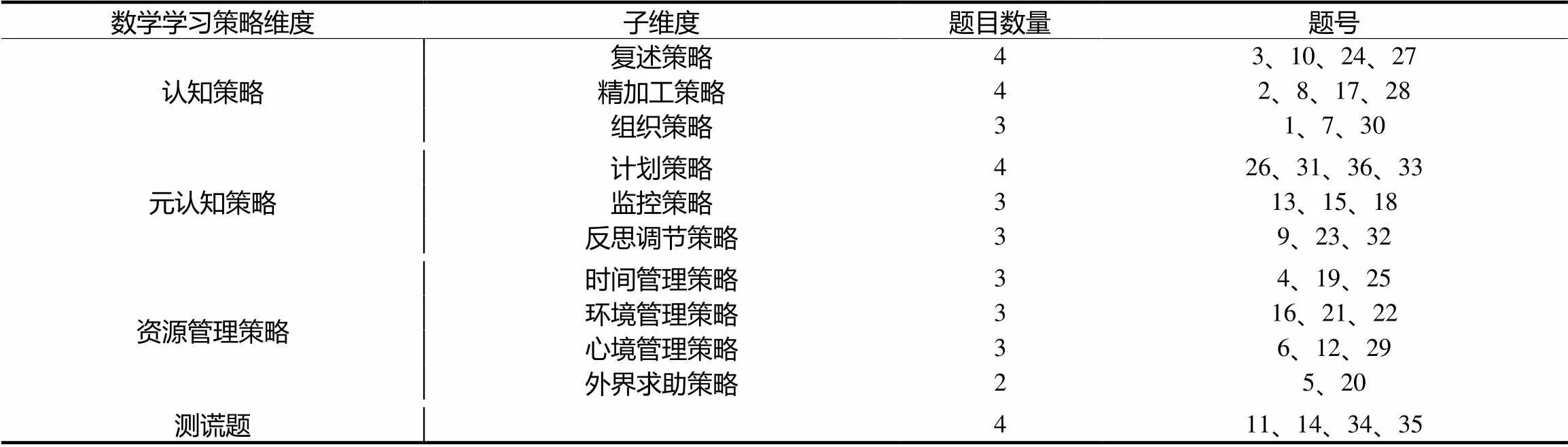
表5 初中生数学学习策略水平调查问卷题目安排（第四版）

注：11题与34题，14题与35题为两两对应的测谎题

7 结 论

“初中生数学学习策略调查问卷”研制过程科学客观，具有良好的信度和效度指标，可作为调查与评价初中生数学学习策略水平的有效工具．

[1] 莫秀锋．初中生数学学习策略的发展特点及可控心理影响因素研究[D]．西南师范大学，2002．

[2] 王光明，佘文娟，宋金锦．基于NVivo10质性分析的高效数学学习心理结构模型[J]．心理与行为研究，2014，（1）：74-79．

[3] 康玥媛，张楠，王光明，等．基高效率数学学习高中生数学成绩的影响路径[J]．心理与行为研究，2016，（3）：352-359．

[4] 王桂云，沈自飞．关于高职生数学学习策略的研究与思考[J]．数学教育学报，2005，14（2）：97-99．

[5] 汤服成，梁宇．小学四~六年级学生数学元认知监控学习策略培养的研究[J]．数学教育学报，2008，17（1）：47-50．

[6] 莫秀锋，刘电芝．初中生数学学习策略的个体差异研究[J]．数学教育学报，2007，16（4）：56-58．

[7] 刘电芝，高岚，钱建国，等．小学生数学学习策略掌握现状分析[J]．数学教育学报，2013，22（6）：27-31．

[8] Dansereau D F.[A]. In: Segal J W, Chipman S F, Glaser eds.[C]. Hillsdale NJ Erlbaum, 1985.

[9] 刘儒德．论学习策略的实质[J]．心理科学，1997，（2）：179-181．

[10] 陈琦，刘儒德．当代教育心理学[M]．北京：北京师范大学出版社，1997．

[11] 刘电芝．小学儿童数学学习策略的发展与加工机制研究[D]．西南师范大学，2003．

[12] 姚志敏．场独立—场依存认知风格对初中生数学学习策略的影响研究[D]．江西师范大学，2008．

[13] 王光明，廖晶，黄倩，等．高中生数学学习策略调查问卷的编制[J]．数学教育学报，2015，24（5）：25-30．

[14] 廖晶，王光明，黄倩，等．高中生高效率数学学习策略特征及对数学学业水平的影响路径[J]．数学教育学报，2016，25（5）：65-70．

[15] Weinstein C E, Palmer D R. Learning and Study Strategies Inventory (High School Version) [EB/OL]. http://www. hhpublishing.com/_assessments/LASSI/. H&H Publishing Company, Inc, 1990.

[16] Pintrich P R. A Manual for the Use of the Motivated Strategies for Learning Questionnaire (MSLQ) [EB/OL]. http://files.eric.ed.gov/fulltext/ED338122.pdf. The Regents of the University of Michigan, 1991.

[17] 刘军，富萍萍．结构方程模型应用陷阱分析[J]．数理统计与管理，2007，（2）：268-272．

附录：初中生数学学习策略调查问卷

亲爱的同学：

你好！为了解初中生数学学习过程中的一些想法和感受，我们邀请你参与此次调查．感谢你的配合．此次调查具体要求如下：

1. 请根据自己的实际情况，填写或选出适合的答案（在答案上画“√”），注意每个问题都需要作答，并且只能选一个答案；

2. 答案为A、B、C、D、E五个选项，每一个备选答案的含义如下：

A 非常符合：并不意味着这一陈述所描述的情况总是发生在你身上，而是指几乎在所有情况下这一陈述对你来说是符合的

B 符合：指在一般情况下这一陈述对你来说是符合的

C 不确定：指半数情况下这一陈述对你来说是符合的

D 不符合：指在一般情况下这一陈述对你来说是不符合的

E 非常不符合：指几乎在所有情况下这一陈述对你来说是不符合的

3. 以下各题答案无好坏对错之分，回答结果只为科学研究所用，不作为其它依据；

4. 此次调查采取匿名做答，我们将对回答结果绝对保密，请务必认真、如实回答每一个问题，你的回答对我们的研究非常重要．

基本信息

学校：   班级：   性别：   年龄：

调查项目

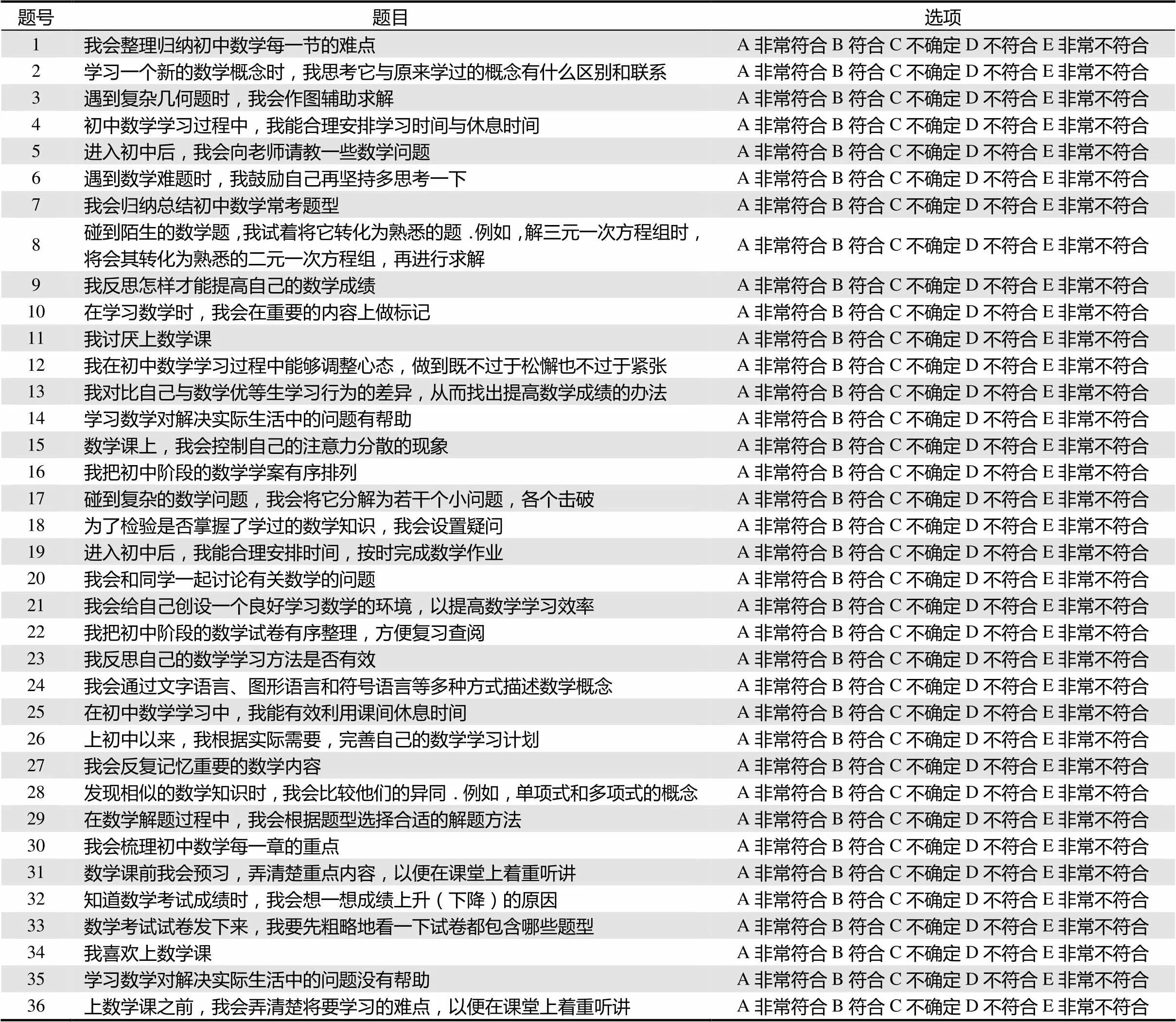
题号题目选项 1我会整理归纳初中数学每一节的难点A非常符合B符合C不确定D不符合E非常不符合 2学习一个新的数学概念时，我思考它与原来学过的概念有什么区别和联系A非常符合B符合C不确定D不符合E非常不符合 3遇到复杂几何题时，我会作图辅助求解A非常符合B符合C不确定D不符合E非常不符合 4初中数学学习过程中，我能合理安排学习时间与休息时间A非常符合B符合C不确定D不符合E非常不符合 5进入初中后，我会向老师请教一些数学问题A非常符合B符合C不确定D不符合E非常不符合 6遇到数学难题时，我鼓励自己再坚持多思考一下A非常符合B符合C不确定D不符合E非常不符合 7我会归纳总结初中数学常考题型A非常符合B符合C不确定D不符合E非常不符合 8碰到陌生的数学题，我试着将它转化为熟悉的题．例如，解三元一次方程组时，将会其转化为熟悉的二元一次方程组，再进行求解A非常符合B符合C不确定D不符合E非常不符合 9我反思怎样才能提高自己的数学成绩A非常符合B符合C不确定D不符合E非常不符合 10在学习数学时，我会在重要的内容上做标记A非常符合B符合C不确定D不符合E非常不符合 11我讨厌上数学课A非常符合B符合C不确定D不符合E非常不符合 12我在初中数学学习过程中能够调整心态，做到既不过于松懈也不过于紧张A非常符合B符合C不确定D不符合E非常不符合 13我对比自己与数学优等生学习行为的差异，从而找出提高数学成绩的办法A非常符合B符合C不确定D不符合E非常不符合 14学习数学对解决实际生活中的问题有帮助A非常符合B符合C不确定D不符合E非常不符合 15数学课上，我会控制自己的注意力分散的现象A非常符合B符合C不确定D不符合E非常不符合 16我把初中阶段的数学学案有序排列A非常符合B符合C不确定D不符合E非常不符合 17碰到复杂的数学问题，我会将它分解为若干个小问题，各个击破A非常符合B符合C不确定D不符合E非常不符合 18为了检验是否掌握了学过的数学知识，我会设置疑问A非常符合B符合C不确定D不符合E非常不符合 19进入初中后，我能合理安排时间，按时完成数学作业A非常符合B符合C不确定D不符合E非常不符合 20我会和同学一起讨论有关数学的问题A非常符合B符合C不确定D不符合E非常不符合 21我会给自己创设一个良好学习数学的环境，以提高数学学习效率A非常符合B符合C不确定D不符合E非常不符合 22我把初中阶段的数学试卷有序整理，方便复习查阅A非常符合B符合C不确定D不符合E非常不符合 23我反思自己的数学学习方法是否有效A非常符合B符合C不确定D不符合E非常不符合 24我会通过文字语言、图形语言和符号语言等多种方式描述数学概念A非常符合B符合C不确定D不符合E非常不符合 25在初中数学学习中，我能有效利用课间休息时间A非常符合B符合C不确定D不符合E非常不符合 26上初中以来，我根据实际需要，完善自己的数学学习计划A非常符合B符合C不确定D不符合E非常不符合 27我会反复记忆重要的数学内容A非常符合B符合C不确定D不符合E非常不符合 28发现相似的数学知识时，我会比较他们的异同．例如，单项式和多项式的概念A非常符合B符合C不确定D不符合E非常不符合 29在数学解题过程中，我会根据题型选择合适的解题方法A非常符合B符合C不确定D不符合E非常不符合 30我会梳理初中数学每一章的重点A非常符合B符合C不确定D不符合E非常不符合 31数学课前我会预习，弄清楚重点内容，以便在课堂上着重听讲A非常符合B符合C不确定D不符合E非常不符合 32知道数学考试成绩时，我会想一想成绩上升（下降）的原因A非常符合B符合C不确定D不符合E非常不符合 33数学考试试卷发下来，我要先粗略地看一下试卷都包含哪些题型A非常符合B符合C不确定D不符合E非常不符合 34我喜欢上数学课A非常符合B符合C不确定D不符合E非常不符合 35学习数学对解决实际生活中的问题没有帮助A非常符合B符合C不确定D不符合E非常不符合 36上数学课之前，我会弄清楚将要学习的难点，以便在课堂上着重听讲A非常符合B符合C不确定D不符合E非常不符合

[责任编校：周学智]

Design of Mathematics Learning Strategies Questionnaire for Junior High School Students

WANG Guang-ming, LIU Dan

(Teacher Education College, Tianjin Normal University, Tianjin 300387, China)

Through the literature review, the existing questionnaires or scales, and the opinions of well-known experts, Junior High School Students’ Mathematics Learning Strategy was divided into three dimensions: cognitive strategies, meta-cognitive strategies and resource management strategy, and we establish an operational definition of 10 sub-dimensions. We form the original questionnaire by the operational definition and the existing questionnaires or scales. Through data collection four times, project analysis, confirmatory factor analysis, exploratory factor analysis, and modify the questions in the questionnaire, eventually forming the. The questionnaire had good reliability and validity index, which could be used as an effective tool to measure the level of mathematics learning strategies for junior high school students.

junior high school; mathematics learning strategies; the design of questionnaires; scale

G449

A

1004–9894（2017）03–0019–06

2017–05–11

天津市2016年度哲学社会科学规划重点课题——立德树人背景下中学生学科核心素养测评——以语数外为例（TJJX16-007）

王光明（1969—），男，天津人，教授，博士生导师，主要从事数学课程与教学论研究．