合作问题解决视角下的数学课程标准的定量研究——基于PISA2015 CPS测评框架

孔凡哲，赵 娜



合作问题解决视角下的数学课程标准的定量研究——基于PISA2015 CPS测评框架

孔凡哲1，2，赵 娜1，2

（1．国家基础教育实验中心，吉林长春 130024；2．东北师范大学教育学部，吉林长春 130024）

数学课程的内在属性既要求合作问题解决（即CPS），又为其培养提供了天然载体．基于PISA2015 CPS测评框架，旨在构建CPS视角下课程标准的评价指标体系，定量刻画课程标准中的CPS呈现类型及其效果．研究表明：尽管标准2011版先于CPS测评框架颁布，但无意之中已经渗透CPS，而且高水平呈现达35.38%，在课程目标、82个案例、实施建议中的呈现效果最好——课程目标中的呈现效果均值达到中上水平，82个案例中的呈现量达到31.71%；就CPS呈现数量而言，课程目标与实施建议、82个案例具有一致性，关联强度型（平方尺度）效应量=0.38非常接近“大”的标准．标准2011版对CPS的渗透与培养，虽有先见之明，但并不彻底，虽有意为之，但仍有较大改进空间．

合作问题解决；数学课程标准；呈现；量化分析；PISA

如众所知，“合作”与“问题解决”是信息社会发展的内在需要和不竭动力，合作问题解决已经成为当今信息社会最基本、最急需的公民素养之一．“合作问题解决是人类区别于动物的三大特征之一，理应成为教育的目标之一．”[1]（Alschuler，1977）

合作问题解决，英文Collaborative Problem Solving（简写CPS），又译“协作问题解决”，1926年国际学术界就有人论及（如日本学者K Ohkubo发表的日文论文[2]）．2011年，S Greiff在伦敦“关于合作问题解决的皮尔森专家组会议”上提出“合作问题解决”评价设想[3]．2013年，经济合作与发展组织（即OECD）将“合作问题解决”列为一种能力（素养），颁布《PISA2015合作问题解决框架草案》[4]，于2015年付诸实测．

2011年12月颁布、2012年3月付诸实施的中国《义务教育数学课程标准（2011年版）》（以下简称“标准2011版”）是否呈现了CPS？若已呈现，其效果如何？正面回答这个问题，需以CPS呈现为主题，对标准2011版进行文本分析．开展此项研究，不仅可以洞察中国义务教育数学课程标准在国际化趋势CPS上的实际水平，而且可助推中国CPS实践操作，对正在修订中的《普通高中数学课程标准》的最终定稿，也具有重要的理论价值和现实意义．

1 背景分析

在“终身学习”思想指导下，联合国教科文组织（UNESO）提出“学会求知、学会做事、学会共处、学会发展和学会改变”五大支柱[5]，“成立专门的学习成果衡量特设工作组（The Learning Metrics Task Force，简称LMTF）”[6~7]，LMTF“2013年确立核心素养指标体系的7个学习领域”[7]，合作、问题解决作为其第5项指标“学习方式与认知”的子领域，被明确提出来[7]．

中国教育部（基教二司）2016年9月14日发布《中国学生发展核心素养》，将“问题解决”作为学生应具备的、具有适应终身发展和社会发展需要的必备品格和关键能力之一，列入“社会参与”的重点之一[8]．而OECD、欧盟、美国、英国、日本、新加坡、芬兰、加拿大、澳大利亚以及中国台湾地区，一致将“团队合作”纳入各自的核心素养指标体系[7]．随着PISA 2015对CPS的实测，CPS及其评价成为国际化趋势．

2 CPS与数学课程

2.1 CPS的内涵

OECD在PISA2015中将CPS定位为：

个体有效地参与由两名或以上成员组成的团队，通过共享理解，达成共识，寻求解决方案，汇集团队成员知识、技能和行动以解决问题的能力[4]．

CPS，源于OECD2003年提出“问题解决的知识与技能”，2010年提出“问题解决能力”，历经两次演变，关注点最终落在问题解决的合作与参与．问题解决的测评从侧重于认知性素养，过渡到强调情感性素养，逐渐发展为以测评社会性素养为核心．

CPS是一个全新的概念，起源于问题解决，指向合作性，聚焦问题解决与合作之间的动态交融，强调在解决问题的个人层面（即在探究和理解、表征和系统化、计划和执行，以及监控和反思4个环节之中），适切融入合作性社会素养，聚焦于建立和维持共识、采取合适行动解决问题，以及建立和维持团队组织形式．CPS立足于个人问题解决素养的基础，全程性地统筹团队智慧，通过理解、共享、情感管理，实现社会交互，强化合作认知．

2.2 CPS与数学课程

CPS作为信息社会必需的一种核心能力，理应成为中小学数学课程的重要培养目标之一．不仅如此，数学课程内容本身也需要发展CPS．

首先，数学课程的部分内容适合CPS，而且是培养CPS的最佳途径．如“算法多样化”体现了数学思维的多元化，要求学生在合作中，交流分析问题的不同角度、分享各自的个性化方法，从而将工具性理解发展为关系性理解．

其次，数学学习的发展性需要CPS．随着学段的提升，数学课程中不少内容逐渐涉及相对复杂的数学活动，在没有更有效的数学工具之前，往往需要采取合作方式加以解决．例如，标准2011版中的包装盒中的数学：如何用一张矩形纸制作一个无盖的长方体盒子，以确保它的容积最大[9]．该问题的本质是一元三次函数最值问题，需用导数理论，但对义务教育阶段的学生而言，仅采取“两边夹”的数学逼近思想，仍可以获得相对理想的近似解，但其计算量大，采用分组合作方式，效果更佳．

最后，CPS有利于培养创新意识和创新能力．在数学学习中，学生经验背景的差异往往导致问题理解的差异，而这种差异恰恰是难得的学习资源：相互的表达与倾听，可以清晰表达自己的观点、全面了解他人的想法，进而摆脱自我中心的思维倾向；相互质疑与批判可以引发思维冲突、激发自我反思、深化认识，激发新灵感，提出新假设．

可见，CPS既符合数学本质的必然要求，也是学生数学学习的自身需要．

3 基于CPS视角的数学课程标准的文本分析工具

CPS作为当今信息社会的一种基本的生存本领，理应成为中小学数学课程的重要培养目标之一．标准2011版在课程“总目标”中明确提出：（学生要）学会与他人交流合作．……养成……合作交流、反思质疑等学习习惯．

标准2011版由“前言”、“课程目标”、“课程内容”、“实施建议”及“附录”组成[9]，明文涉及“合作问题解决”的内容和要求，共17次，出处既有目标设定，又有评价建议，既有教学设计，又有教学建议．这些内容彰显标准2011版对“合作问题解决”的重视（是有意？还是无意的？尚不能确认）．但是，标准2011版并没有明确提出CPS，也没有对其作详细的诠释说明．

基于OECD 2015 PISA CPS的视角进行深入分析，有助于诠释CPS在标准2011版中的理论呈现，更利于标准2011版的实践操作．

3.1 研究设计

采用“定量刻画、定性诠释”方法，对标准2011版中CPS的呈现进行定量分析：

首先，遵循《PISA2015合作问题解决框架草案》[4]，正确诠释、合理解读CPS的内涵；其次，基于CPS内涵，综合考虑标准2011版的数学属性，明晰CPS呈现水平的主要影响因素；第三，建构CPS呈现效果的分析框架及其评判标准；第四，编码，一方面，利用已建构的分析框架，逐条提取标准2011版中涉及CPS的内容并编码；另一方面，根据CPS呈现水平评判标准，对已提取的CPS呈现载体进行二次编码，确定其呈现类型及水平；最后，分析，即，在两次编码的基础上，定量刻画、定性诠释标准2011版中CPS的呈现及其效果．

3.2 影响CPS在标准2011版中呈现水平的要素分析

“CPS是由合作技能和PS（即问题解决能力）联合形成的宏观二维能力．其中，合作技能在CPS中合作起先导作用”[10]，而建立维持共识、采取合适的行动解决问题、建立和维持团队组织形式，CPS的这3种核心能力实际上源于合作和个体层面问题解决过程的结合．从而，PISA2015将3种核心能力和4种个人层面的问题解决能力，作为矩阵的纵维、横维，构成CPS的12种具体技能（见表1）．

表1 PISA 2015 CPS的测评矩阵

注：这是《PISA2015合作问题解决框架草案》给出的CPS评判标准，在2015PISA测试中得以成功使用，得到国际上普遍认可．

依据CPS内涵，综合考虑数学课程标准的文本属性，可以发现，CPS在课程标准中的呈现水平，取决于3个关键要素：

其一，CPS内涵的符合度．即呈现时是否关注合作、问题解决以及两者之间的动态联系．

其二，数学内涵的符合度．即呈现是否符合数学内容、数学学习的发展性需求等．

其三，功能指向的差异性．即分为直接功能和间接功能，亦即，功能指向侧重于学习性，还是侧重于情感性．

3.3 CPS呈现类别和水平及其标准界定

定量刻画课程内容，其实是一件十分困难的事．

在课程标准中，CPS的呈现优劣与否，主要取决于文本是清晰、明确地表述，还是隐含、模糊地表述．

按照模糊数学思想，借鉴统计学“抓主要矛盾，结论在一定程度内能接受即可，未必100%”的观点，可以将课程标准对于CPS的呈现，将其效果的等第区分为“呈现效果良好、呈现效果一般、呈现效果差”；按呈现方式的显现与否（聚焦是否更有利于课程实施、更有利于达成预期的课程目标），区分为显性呈现和内含呈现两种方式（见表2）．

表2 标准2011版CPS呈现水平的评判标准

从而，在课程标准中，CPS的呈现可分为3个水平、2种类别共计6种情况，涵盖CPS呈现的各种情况（见表3）．

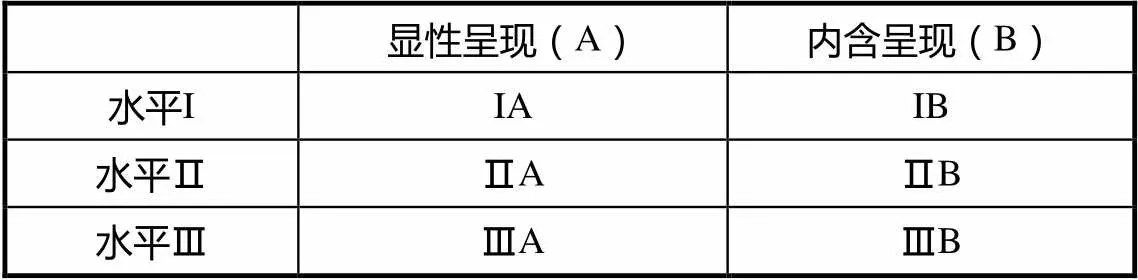
表3 CPS在课程标准中的呈现的类别与水平

其中，水平I的目标指向在于更好地实现PISA2015 CPS测评矩阵（即表1）中12项能力的培养，亦即，若课程标准能效果良好地呈现CPS，则有助于培养学生完备的CPS．其中的IA、IB分别代表显性的I级水平呈现、内含的I级水平呈现．

而水平Ⅱ的目标诉求，在于帮助学生形成12项能力中的部分能力．其中的ⅡA、ⅡB分别代表显性的Ⅱ级水平呈现、内含的Ⅱ级水平呈现．

水平Ⅲ意味着，数学课程内容本质上适合培养CPS，但实际呈现却空空如也．进一步区分为，显性的Ⅲ级水平呈现，即ⅢA，以及内含的Ⅲ级水平呈现，即ⅢB．

如果说PISA2015的CPS是能力评价指向，那么，课程呈现中的CPS则是能力培养指向，即CPS的培养途径．这就要求CPS的课程呈现，除了关注“CPS是否生成”这个结果，也应重视“CPS如何生成”的过程；除了关注CPS的整体机制，也应重视CPS的具体行为．亦即，基于培养的CPS课程呈现，既包括将综合性、过程性的CPS在一个课程内容或一次数学活动（问题情境）中加以体现（即水平I），也包括将具体的某一项或几项能力在不同的课或活动中加以呈现（即水平Ⅱ或Ⅲ）．这与前文构建的分析指标及评价标准相互一致．

4 标准2011版的CPS呈现的定量分析

利用CPS呈现水平分析框架（表1、2、3），逐条提取标准2011版中涉及CPS的内容并编码；根据“CPS呈现水平的评判标准”二次编码．在两次编码的基础上，分析标准2011版中CPS的呈现（量化数据）及其效果等级．

4.1 标准2011版中CPS呈现的具体分析

4.1.1 “课程目标”的CPS呈现分析

在标准2011版“课程目标”内容中，依据“CPS呈现水平的评判标准”，对其中出现的、总计11次的CPS呈现，进行编码，例如：

“经历与他人合作交流解决问题的过程，尝试解释自己的思考过程”，标准2011版中的这个表述，既提出解决问题能力培养，又明确要求学生“合作”，亦即，培养学生合作问题解决的能力．因此，编码为IA，即CPS显性的Ⅰ级呈现．“课程目标”中类似的呈现共4次；

“能针对他人所提的问题进行反思，初步形成评价与反思的意识”，该表述虽没有明确提出培养学生合作问题解决的能力，但对来自他人的“问题”进行“反思”“评价”，是合作问题解决必不可少的环节，也是CPS综合体必需的能力要素，因此，编码应为IB，即内含式的Ⅰ级呈现CPS．“课程目标”中类似的呈现共2次；

“敢于发表自己的想法、勇于质疑、敢于创新，养成……合作交流等学习习惯”，表述中虽提到“合作”，但仅将“合作”定位于“学习习惯”，尚未直接指向问题解决（能力），故编码应为ⅡA，即显性的Ⅱ级呈现CPS．“课程目标”此类呈现仅出现1次；

“在他人的鼓励和引导下，体验克服困难、解决问题的过程，相信自己能够学好数学”，表述中没有提及“合作”，但“他人的鼓励和引导”暗指解决问题需要与他人“合作”，即，解决问题的过程中隐藏合作，故编码应为ⅡB，即内含式的Ⅱ级呈现．“课程目标”中类似的呈现共4次．

按上述统计方法，“课程目标”中的CPS呈现水平及类型分布如表4所示，从中可知，标准2011版在“课程目标”中CPS的呈现属于I级、Ⅱ级，而且数量差异不大，无Ⅲ级呈现．其中，I级显性呈现达到36.4%，且集中于“问题解决”目标维度，这与CPS内涵一致，即在问题解决中强调合作；Ⅱ级中的内含呈现达到36.3%，集中于“情感态度”目标维度，侧重情感体验的目标更适合隐性、简略地体现CPS内涵．

表4 “课程目标”的CPS呈现水平及类型分布

将CPS呈现上述结果编码，按标准2011版“课程目标”的4个组成要件“知识技能”、“数学思考”、“问题解决”、“情感态度”进行分类，可以发现：CPS仅在“问题解决”与“情感态度”中呈现．其中，在“问题解决”中的呈现均属于I级，其效果比较理想．把“合作”作为“问题解决”的分目标提出，明确规定了CPS的方向与归属，这与PISA将CPS作为测评项，有异曲同工之妙．“情感态度”中CPS的呈现，侧重于情感体验的目标指向，呈现效果一般．而“知识技能”与“数学思考”并没有涉及CPS，尤其是，“数学思考”作为旨在培养学生数学核心素养的目标，并没有针对合作问题解决的能力提出任何目标要求．事实上，CPS测评矩阵中提出的“探究与理解”、“表征和系统化”、“监控与反思”，都需要进行一定程度的数学思考．在“数学思考”中提出“合作问题解决”目标，不仅是学生学习所必要的，而且是数学课程自身的需要．“课程目标”各领域中CPS不同呈现水平的数量分布如图1．

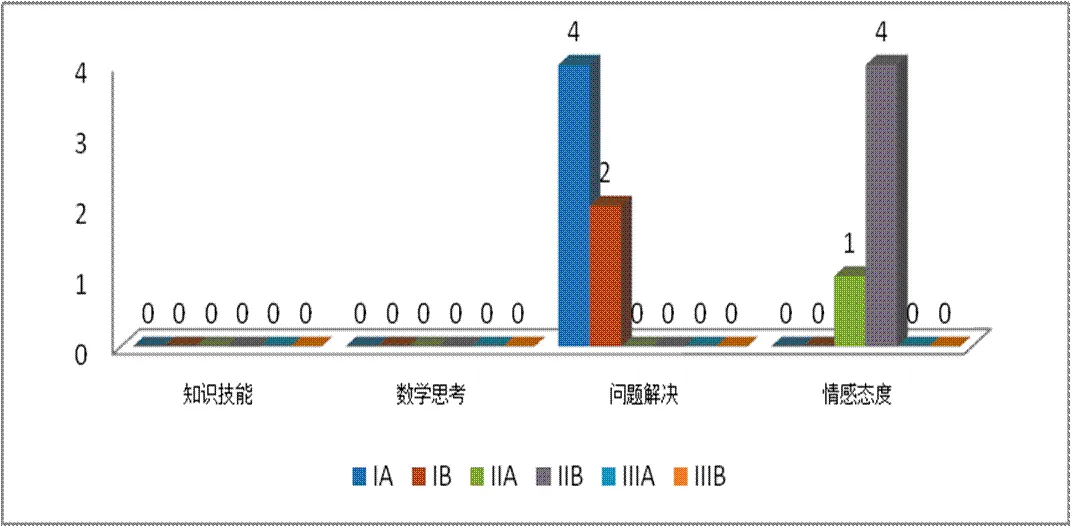
图1 “课程目标”各领域中CPS不同呈现水平的数量分布

这表明，就CPS而言，标准2011版“课程目标”仍有较大的改进空间．

4.1.2“课程内容”的CPS呈现分析

按前文的编码规则，对“课程内容”的文本进行分析．如“通过试验、游戏等活动，……并能进行交流”，表述中既没提到“合作”，也没提及“问题解决”，但“试验、游戏等活动”必然包含问题解决，“交流”也必然需要合作，但文本并没有呈现，故编码为ⅢA，即CPS显性的Ⅲ级呈现．“课程内容”中类似的呈现共计4次．

汇总发现，在“课程内容”中，CPS的呈现共8次，其中，Ⅰ级、Ⅱ级、Ⅲ级均有涉及，Ⅲ级的显性呈现占50%，Ⅰ级呈现占37.5%（均为内含呈现），而Ⅱ级呈现仅占12.5%，属于显性呈现．

按数与代数、图形与几何、统计与概率、综合与实践4个内容领域进行分类，CPS在数与代数、综合与实践和统计与概率中均有呈现．虽然数与代数、综合与实践中CPS呈现量少，仅占25%，但其效果良好，数与代数中CPS呈现水平均为IB，综合与实践中CPS呈现水平则为IB、ⅡA；统计与概率中CPS呈现量相对多，占50%，但其呈现效果差，均属于Ⅲ级的显性呈现．

事实上，统计与概率内容的操作性很强，其学习不仅需要而且更适合CPS，但标准2011版对此却无充分体现．

在图形与几何中，CPS没有任何体现（图2），这似乎与标准研制者认为义务教育几何学习内容本身一般不需要合作密切相关．

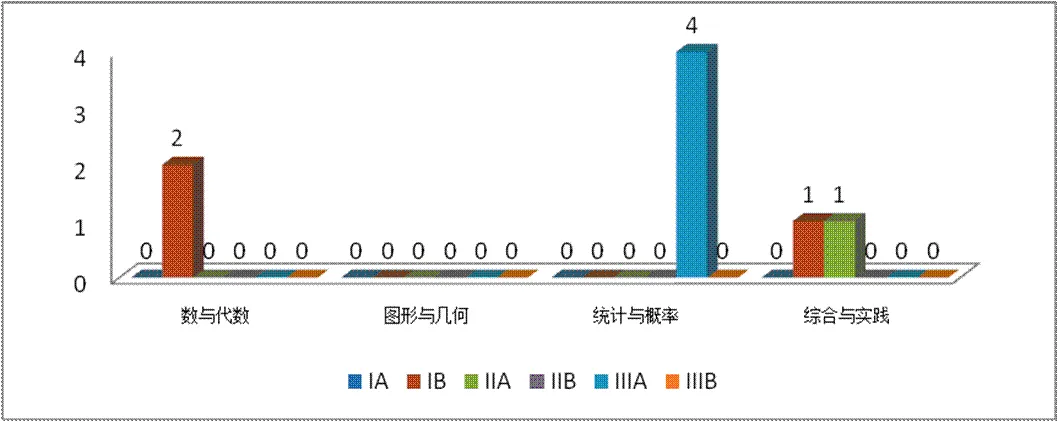
图2 “课程内容”各领域中CPS不同呈现水平的数量分布

与一般的数学课程内容相比，以课程内容出现的CPS，作为一种能力，其侧重点在于依附其它课程内容，达成其培养目的，而非其内容本身．标准2011版中的“课程内容”更强调对数学课程内容及其目标要求进行明确阐述，无法高效呈现CPS，应该与相关内容未必仅需合作问题解决的学习方式（或呈现方式）密切相关．不过，标准2011版中，一些课程内容对CPS仍有较理想的呈现，如数与代数中的“算法多样性”以及数学建模等实践性强的内容，均有利于CPS呈现，而且，标准2011版对此也有良好的呈现效果．

4.1.3 “实施建议”的CPS呈现分析

按前文的编码方式，对“实施建议”分析发现，在“实施建议”中，CPS的呈现量相对较多，达20次，多属于Ⅱ级．其中，显性呈现11次（占55%）；内含呈现仅5次（占25%），多集中于“教学建议”，但其他3部分也有涉及；I级显性呈现4次（占20%），均出现于“教学建议”中．

按“实施建议”的4个组成要件“教学建议”、“评价建议”、“教材编写建议”及“课程资源开发与利用建议”进行分类，可以发现：

就“实施建议”而言，CPS呈现集中于“教学建议”（14次，占70%），多属于Ⅱ级，或显性呈现，或内含呈现；在“评价建议”、“教材编写建议”及“课程资源开发与利用建议”中，CPS呈现量呈递减下降趋势，均是显性的Ⅱ级呈现（见图3）．这体现出，标准2011版更关注CPS的教学落实．

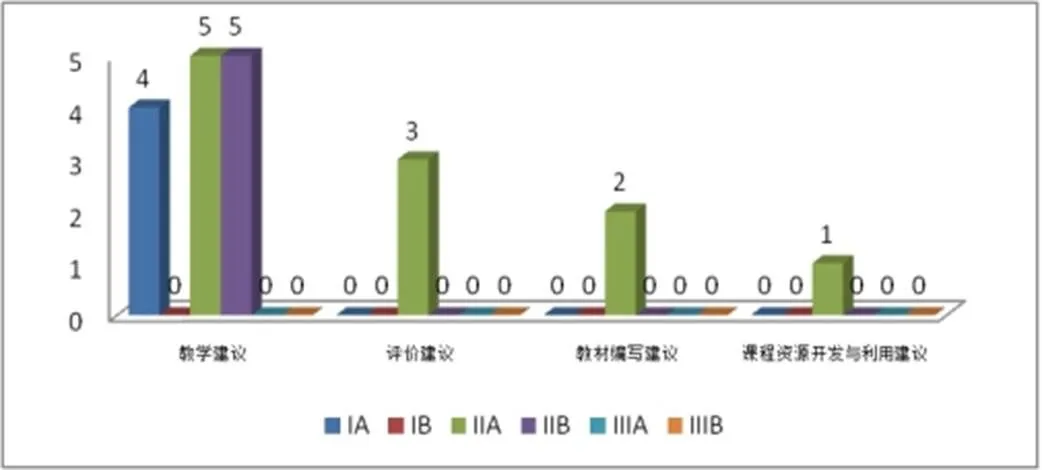
图3 “实施建议”4个建议中CPS不同呈现水平的数量分布

特别地，标准2011版针对综合与实践的教学建议，明确提出“教师在教学设计和实施时应特别关注的几个环节是：问题的选择，问题的展开过程，学生参与的方式，学生的合作交流，活动过程和结果的展示与评价等”，将问题解决全程贯穿于合作交流之中，这与OECD提出的CPS内涵不谋而合，而且，标准2011版设置专门领域培养CPS，实属先见之举，早于OECD数年．

可见，标准2011版十分关注CPS培养，但缺乏对其进行测评的意向，也缺少在教材中有效渗透CPS的针对性要求，尤其在“数学思考”与“问题解决”课程目标的相关评价建议中，并没有提及有关合作问题解决评价的任何内容．

4.1.4 “案例”的CPS呈现分析

按前文的编码方式对“案例”进行分析．如，标准2011版的例34“测量一个土豆的体积”，这个真实情景问题比较适合合作方式，但其文本对此并没有任何表述，编码为ⅢB更妥当，即CPS的内含式Ⅲ级呈现．类似的呈现先后出现5次（如表5所示）．

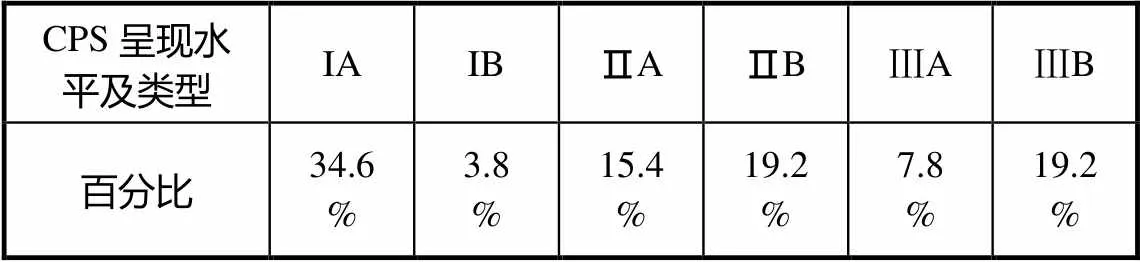
表5 “案例”的CPS呈现水平及类型分布

标准2011版附录中给出82个案例，其中，26个已作为CPS载体：I级呈现占38.4%，其中的90%是显性呈现；Ⅱ级呈现占34.6%；Ⅲ级呈现占26.9%，其中的71.43%是内含呈现（案例中实际具备呈现CPS的条件及需要，却并未显性呈现）．

在标准2011版中，82个案例呈现CPS的案例占31.71%，表明标准2011版有意渗透CPS，这与OECD的理念不谋而合．当然，其中的部分呈现仅停留在提出合作的形式要求，而没有从CPS视角思考数学内容及其课程教学设计．

4个课程领域均涉及CPS，虽覆盖面广，但其渗透强弱不一、差异显著：

统计与概率、综合与实践领域中，CPS呈现量可观（依次为：9次，占34.6%；8次，占30.8%），其呈现效果为I级或Ⅱ级呈现，优于其他课程领域．这取决于其课程内容的特殊性，特别是对合作式的问题解决的目标要求（见图4）．

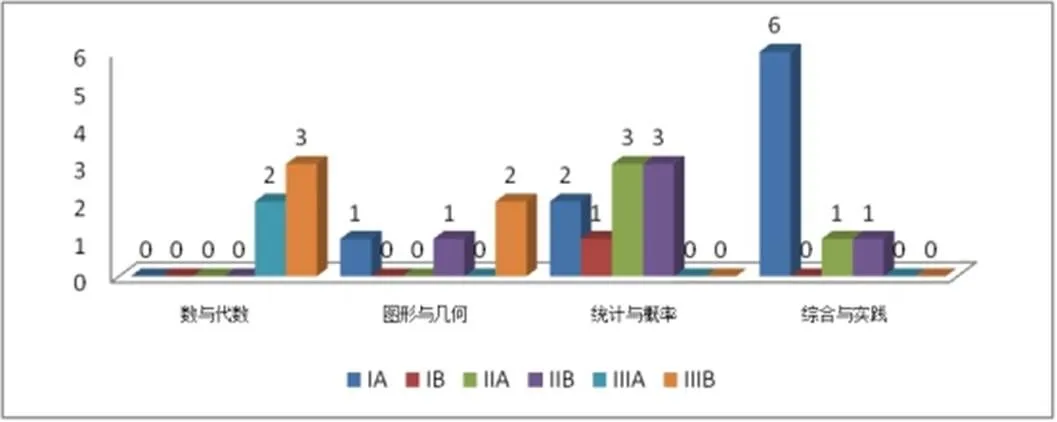
图4 “案例”所属的不同领域中CPS呈现量的分布

将上述已编码的CPS呈现按案例所在的课程内容领域分类，可以发现，数与代数、图形与几何领域中，CPS呈现量相对较少（依次为19.2%、15.4%），多属于Ⅲ级呈现，呈现效果差，明显反映出，课程设计者期望这些内容的学习更侧重独立思考和自主探究．而诸如例34“测量一个土豆的体积”完全可以采用合作问题解决方式，比较适合明确提出CPS培养的相关要求．

事实上，数与代数、图形与几何渗透CPS的空间其实比较大，如，标准2011版在案例35“图画还原”中，明确“可以分小组进行”、“小组活动时，可以先讨论”、“小组成员共同操作，进行比较”等要求[9]，类似内容在图形与几何其实不少．如何将CPS渗透于不同的课程内容领域，整体提高课程标准对CPS的呈现水平，保障其培养举措，是数学课程标准修改完善（以及研制其它版本的课程标准）的努力方向．

4.2 标准2011版中CPS呈现的整体状况

4.2.1 标准2011版中的CPS呈现的各水平分布状况

汇总前文的相关数据可以发现，标准2011版各部分中的CPS呈现总计65次，各呈现水平的分布状况如表6所示．

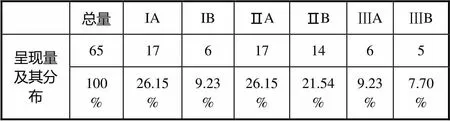
表6 标准2011版CPS呈现水平分布1

按标准2011版除“前言”之外的所有组成要件“课程目标”、“课程内容”、“实施建议”、“案例”进行统计，数据的分布状况如图5所示：

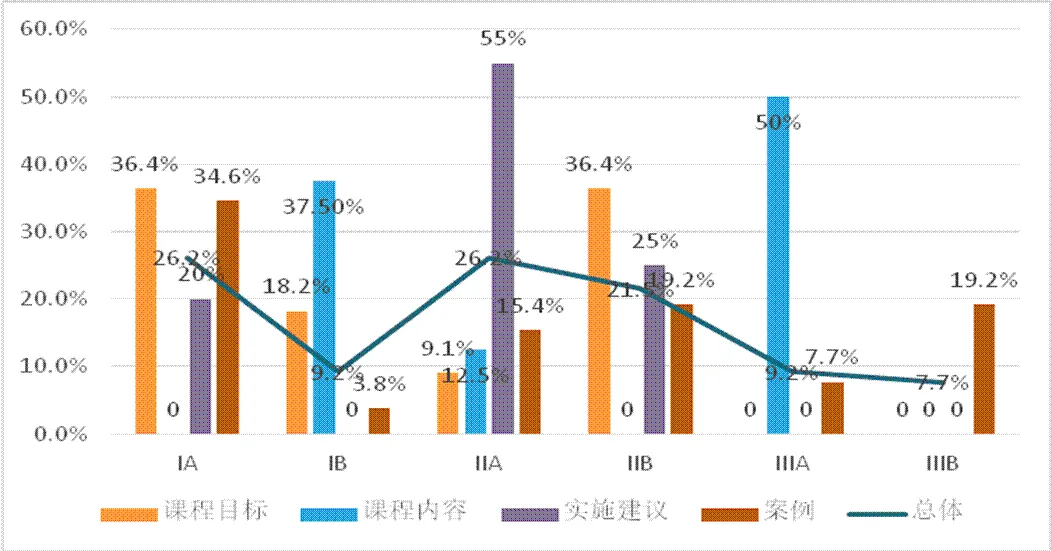
图5 标准2011版各部分的CPS呈现水平数量分布

IA级呈现占26.2%，其中，“课程目标”、“实施建议”、“案例”相对一致（“实施建议”稍低一点）；

IB级呈现仅占9.2%，其中，“课程目标”、“课程内容”相对一致，且“课程内容”远高于总体水平值；

ⅡA级呈现占26.2%，其中，“课程目标”、“课程内容”、“案例”与“实施建议”相对一致（总体呈递增趋势）；“实施建议”中的ⅡA级呈现的比例，远高于（标准2011版的）整体水平；

ⅡB级呈现占21.5%，其中，“课程目标”、“实施建议”、“案例”相对一致（呈递减趋势）．

就CSP呈现水平从高到低的走势看：“课程目标”、“案例”与总体水平比较一致（部分略有波动）；“实施建议”与总体水平，除了ⅡA水平差异显著外，其它几个水平相对一致；“课程内容”与总体水平差异十分显著，尤其是IB、ⅢA差异十分显著．

这表明，就标准2011版各部分中的CPS呈现而言，呈现效果最好的是“课程目标”、“案例”，其次是“实施建议”．

4.2.2 标准2011版中CPS呈现的各领域分布状况

为更好地量化分析，现对IA、IB、ⅡA、ⅡB、ⅢA、ⅢB六级呈现，依次赋值5、4、3、2、1、0，其中，“5”指IA级呈现，即效果好的呈现，有助于培养学生的CPS．依次类推，“0”指ⅢB级呈现，即标准2011版中，本有好的呈现载体，却并未呈现，或错误呈现．

对“课程目标”、“课程内容”、“实施建议”和“案例”中CPS的呈现，进行赋值统计，获得标准2011版中CPS呈现效果的数据分布如表7所示．

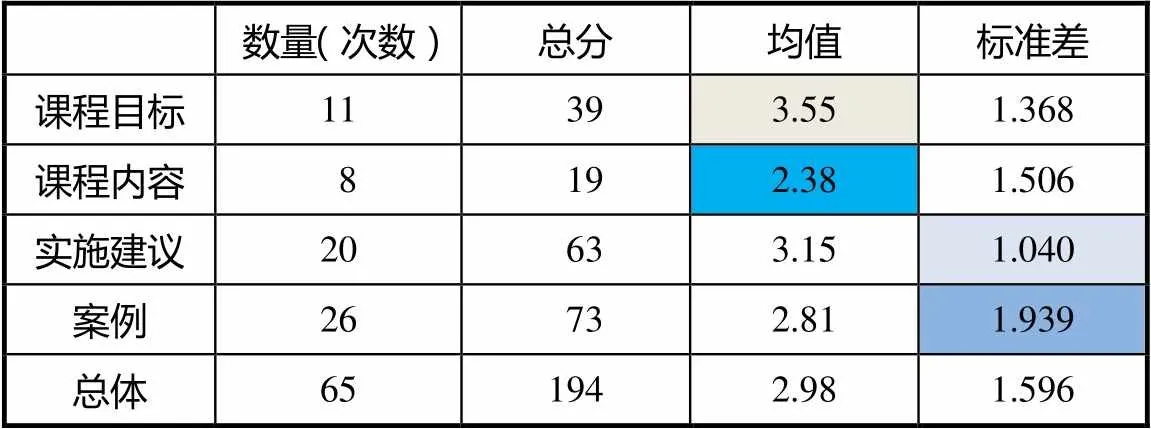
表7 标准2011版CPS呈现水平分布2

就呈现量而言，82个“案例”中，CPS呈现量最可观，占31.71%，“课程内容”中的CPS呈现量较少，仅占12.31%；就效果而言，“课程目标”中的CPS呈现效果最好（均值3.55，介于赋值4与3之间，处于“中上等”水平），“课程内容”中的CPS呈现效果最差（均值2.38，介于赋值3与2之间，处于“中下等”水平）．

就离散程度而言，在“实施建议”“课程目标”中，CPS的呈现分布相对集中（=1.040，=1.368），而“案例”中CPS的呈现分布比较分散（=1.939）．

这与标准2011版各部分内容的具体要求密不可分．事实上，“实施建议”和“课程目标”均是对课程实施的整体描述，不同的实施环节大多可渗透CPS，而“案例”涉及4个课程领域的数学内容，由于其所涉及内容的特殊性，并非都需要体现CPS要求，这与课程标准设计者期望若干数学内容需要学生独立思考、自主探究直接相关．

图6进一步印证了前文的结论：“课程目标”中的CPS呈现量虽不多，但呈现效果最好；“实施建议”中的CPS呈现量与效果皆较好；“案例”中的CPS呈现量虽最多，但其效果相对较差，而“课程内容”中的CPS呈现量及呈现效果均最差．

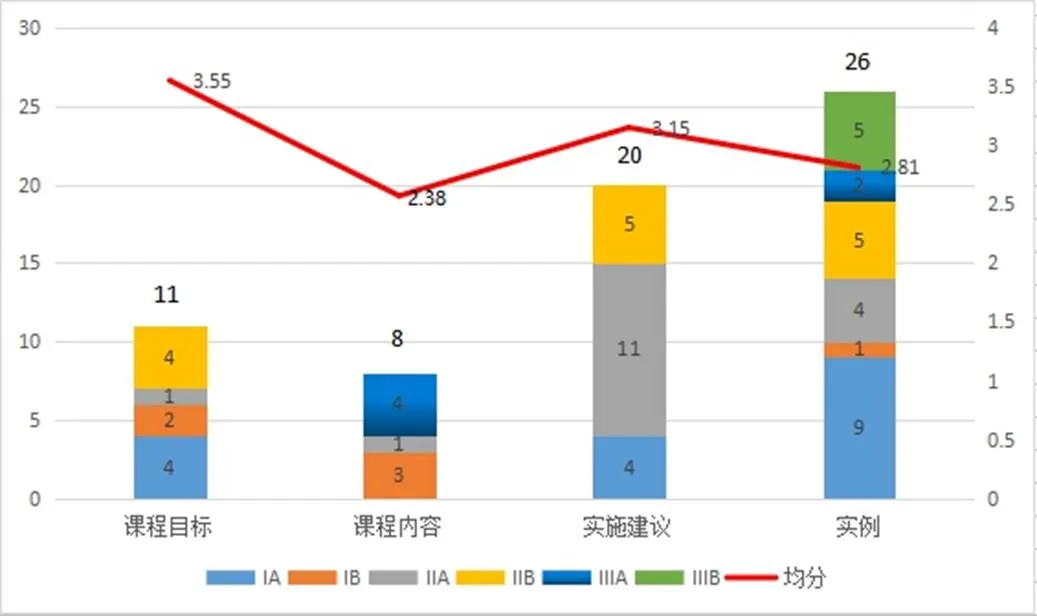
图6 标准2011版中CPS呈现状况的数据分布

进一步分析可见，“课程目标”中的CPS呈现总体效果良好，得益于单个CPS呈现的水平高，而非呈现总量，亦即，“课程目标”中的CPS呈现“少而精”；“课程内容”中的CPS呈现总效果同时受制于单个CPS的呈现水平与呈现总量，亦即，“少且差”——数量少且呈现水平较低；与“实施建议”相比，虽“案例”中呈现总量多，但其呈现水平分布均匀，且低水平呈现较多，而“实施建议”中CPS呈现多集中于I、Ⅱ级水平，故，就CPS呈现总体效果而言，“实施建议”优于“案例”．

4.2.3 CPS在标准2011版中呈现的一致性分析

（1）CPS呈现类型及水平分布的一致性分析．

如图7所示，标准2011版中CPS的IA级、ⅡB级呈现中，“课程目标”与“实施建议”、“案例”表现出良好的一致性，即“课程目标”中呈现CPS，“实施建议”与“案例”中也有相应体现．

图7 CPS呈现类型及水平的整体趋势

CPS的IB级呈现中，“课程目标”与“课程内容”、“案例”具有一致性，二者的CPS呈现量大体一致．

CPS的ⅡA级呈现中，“课程目标”、“课程内容”、“实施建议”、“案例”4者之间的一致性并不高，亦即，虽然“课程目标”、“课程内容”中仅有一处呈现CPS，但在“实施建议”与“案例”却大量呈现了CPS．

CPS的Ⅲ级呈现中，“课程目标”、“课程内容”、“实施建议”、“案例”4者之间相对一致．

（2）CPS呈现类型及水平整体呈现趋势的一致性分析．

就五级呈现水平从高到低的总趋势而言：

“案例”与“课程目标”之间的一致性基本一致，虽在Ⅲ级呈现中违背了“课程目标”的意图；

“实施建议”与“课程目标”在整体上是基本一致的，但在ⅡA级存在显著差异；

“课程内容”与“课程目标”中CPS呈现类型及水平一致性较差，即，“课程目标”中多高水平、少低水平呈现，而“课程内容”与之几乎相反，亦即，高水平呈现少，低水平呈现多．

4.2.4 课程总目标与阶段目标中CPS呈现的一致性分析

如图8所示，在总目标和阶段目标中，CPS呈现具有良好的一致性：

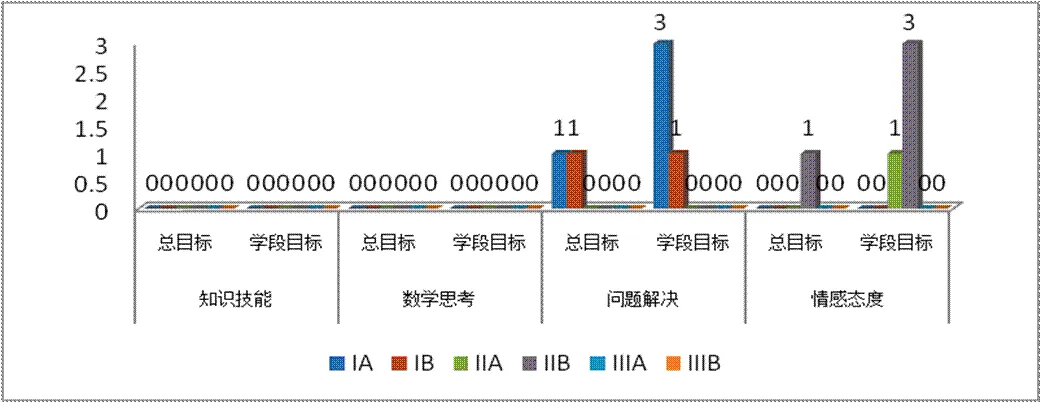
图8 “总目标”和“学段目标”中CPS在各学习领域的呈现情况

“问题解决”总目标中多为I级呈现，阶段目标中也同样以I级呈现；“情感态度”总目标中多为Ⅱ级呈现，阶段目标也以该类型及水平呈现．在阶段目标中，递进式二次呈现总目标中的要求，有利于持续连贯地培养学生的CPS．如“问题解决”总目标中明确指出“学会与他人合作交流”、“初步形成评价与反思的意识”，而阶段目标中递进式提出“体验与他人合作交流解决问题的过程”；“情感态度”总目标中规定学生要养成“合作交流”的学习习惯，而阶段目标中也提出“在他人的鼓励和引导下，体验克服困难、解决问题的过程”……[9]

4.2.5 “课程内容”与“案例”中CPS呈现的一致性分析

如图9所示，4个领域的“课程内容”与其相应的“案例”，彼此的CPS呈现不具有一致性：

数与代数领域，虽“课程内容”对CPS予以较好呈现，但其相应“案例”中的呈现效果差；

图形与几何领域，“课程内容”并没有呈现CPS，但其相应“案例”中却有一处呈现，而且效果良好；

统计与概率领域，“课程内容”的CPS呈现效果差，但其相应“案例”中却大量呈现CPS，而且呈现效果良好；

综合与实践领域，“课程内容”与“案列”中均呈现CPS，但“课程内容”的呈现量远远低于其“案例”中的呈现．

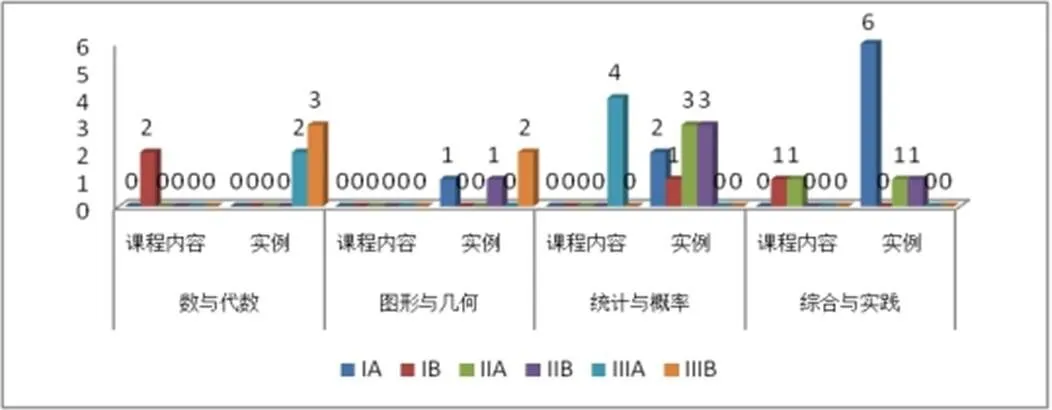
图9 “课程内容”和“案例”中CPS在各学习领域的呈现数据分布

4.3 CPS呈现的相关性分析

CPS呈现在整体、课程目标、课程内容、实施建议和案例中的相关性如表8所示．

表8 CPS呈现在“整体”“课程目标”“课程内容”“实施建议”和“案例”中的相关性

注：*.在0.05水平（双侧）上显著相关；**.在0.01水平（双侧）上显著相关

据表8，（标准2011版的）整体与“课程目标”、“实施建议”、“案例”的CPS呈现存在显著相关（=0.941**/ 0.933**/0.972**），其中，整体与“案例”的相关性最显著．

整体与“课程目标”、“实施建议”、“案例”的CPS在数量呈现上具有良好的一致性．

“课程目标”与“实施建议”、“案例”的CPS呈现存在显著相关（=0.821*/0.932*），即“课程目标”与“实施建议”、“案例”中的CPS呈现数量，分别具有一致性．

特别地，“课程目标”与“案例”的CPS呈现，按照Ferguson（2009）给出的社会科学领域大小判断标准（0.20，小；0.25，中；0.64，大）[11]，其效应量=0.38，介于水平“中”与“大”之间，更接近“大”的水平，这表明，“案例”中CPS呈现与“课程目标”中CPS呈现，彼此有高的效应．

由=0.854*可知，“实施建议”与“案例”的CPS呈现数量具有相关性，即“实施建议”与“案例”中的CPS呈现数量存在一定的一致性．

“课程内容”与“实施建议”、“案例”的CPS在数量呈现上不存在一致性．

总之，统计学意义表明，在CPS呈现数量上，（标准2011版的）整体、“课程目标”、“实施建议”、“案例”具有一致性，效果相对较好；但“课程内容”中的CPS呈现量少，而且效果差．

5 基本结论与讨论

合作问题解决能力（CPS）作为信息社会必不可少的一种基本素养，是世界各国的普遍共识．加强学生CPS培养，是亟待解决的重要课题．

（1）标准2011版有意渗透CPS，有先见之明，这与PISA发展趋势完全一致，甚至说，对CPS的提出，中国标准2011版是有贡献的．

尽管OECD 2013年才明确提出CPS，但2011年12月审定的中国标准2011版已在许多方面予以很好体现，有先见之明．标准2011版不限于表层化呈现CPS，而且，在某些领域、内容中，高效呈现了CPS，尤其在“课程目标”中提出的CPS要求与PISA2015高度一致．如，其关于“探索”一词的解释：

探索：独立或与他人合作参与特定的数学活动，理解或提出问题，寻求解决问题的思路，发现对象的特征及其与相关对象的区别和联系，获得一定的理性认识[9]．

特别地，2008年11月，应美国政府邀请，以史宁中教授为首的中国数学课程标准修订人员及有关专家，参加在美国华盛顿召开的美中数学教育专家会议．在会上，就刚修订完成的标准修订稿（即标准2011版颁布前的版本），中国专家与美国学者进行了深入交流．同时，国内有学者将标准2001版、标准2011版翻译成英文介绍到国外．标准2011版虽没明确提出CPS，但可以推断，标准2011版“课程目标”、“案例”等中已呈现的相关内容，对PISA 2015明确提出CPS，有可能有借鉴参考价值，只是尚未掌握确凿的一手证据而已．

（2）建议课程标准辅以恰当的内容载体及评价标准以确保CPS的良性物化．

研究表明：标准2011版中，以“课程目标”为基准，“案例”对CPS的要求与目标非常吻合（=0.932*），“实施建议”与其比较一致（=0.821*），而“课程内容”中CPS的呈现与其相悖，一致性差；同时，“评价建议”中的CPS呈现仅3处，均属中低级水平．

可见，标准2011版有意培养CPS，但既缺乏内容载体，也缺少测评意向，即使在适合呈现CPS的“统计与概率”、“综合与实践”领域，也没有适时呈现；在“数学思考”与“问题解决”标准目标的相关评价建议中，也没有提及有关CPS评价的任何内容．

按古德莱德（John Goodlad，1920—）的课程层次观，从课程设计到实施过程往往是“衰减”的，尤其是课程实施中更易衰减．要想达成CPS的培养目标，标准2011版更需要在设计中，使“课程内容”、“实施建议”、“案例”中的CPS呈现略高于“课程目标”，至少保持一致．

标准2011版中，与“案例”中CPS的理想呈现相比，其他领域则有待提高．

（3）CPS在标准2011版中的呈现既要体现自身内涵，更需符合数学本质．

在课程标准中呈现CPS，不仅要符合CPS自身的内涵要求，更应体现数学的学科属性，并非所有数学内容都必须经过合作、问题解决才可掌握．就标准2011版而言，统计与概率、综合与实践的内容，需要学生集体合作、体验过程、积淀经验，而数与代数、图形与几何的内在逻辑，有时更需要学生独立思考、抽象内化．讨论CPS的课程教材呈现，不能片面强调数量与效果，更应理性权衡内容载体的教学内涵与数学学科属性．特别地，对“实践与综合”的研究非常薄弱，哪些内容更适合“实践与综合”领域的CPS呈现，国内现有的研究才刚刚起步．

（4）按学段与内容提出CPS的教学建议，更利于CPS的落实力度．

针对教学建议等，标准2011版仅提出整体建议．就CPS的课程物化及教学落实而言，按学段提出教学建议，其指导性更强；按内容领域提出教学建议，更能兼顾数与代数、图形与几何、统计与概率、综合与实践领域的内容差异，其针对性更强．

总之，无论义务教育数学课程，还是高中数学课程，都需要直面信息社会公民必需的CPS．提升数学课程标准对CPS的呈现水平，需要进一步探索CPS恰当的课程样态及实施路径．标准2011版对CPS的渗透与培养，虽有先见之明，但并不彻底，虽有意为之，但亟待完善．进一步改善标准2011版及其实验教科书中的CPS呈现效果，才能切实提升中国学生合作问题解决能力的整体水平．

以主题为单位开展课程标准文本的定量研究，是一种新范式．

[1] Alschuler A, Mcmullen R, Atkins S, et al. Collaborative Problem Solving as an Aim of Education in a Democracy: The Social Uteracy Project [J]., 1977, 13(3): 315-327.

[2] Ohkubo K. A Study on Teaching Composition for Children with PDD Focus on Collaborative Problem Solving [J]., 1926, 3(1): 65-108.

[3] Greiff S.[M]. London: Pearson Expert Group Meeting on Collaborative Problem Solving, Rozhledy, 1964.

[4] OECD. The PISA2015 Draft Collaborative Problem Solving Framework [EB/OL]. http://www.oecd.org/pisa, 2013- 09-17.

[5] 雅克·德洛尔．教育—财富蕴藏其中[M]．联合国教科文组织总部中文科译．北京：教育科学出版社，1996．

[6] 黄四林，左璜，莫雷，等．学生发展核心素养研究的国际分析[J]．中国教育学刊，2016，（6）：8-14．

[7] 林崇德．21世纪学生发展核心素养研究[M]．北京：北京师范大学出版社，2016．

[8] 一帆．《中国学生发展核心素养》总体框架正式发布[J]．教育测量与评价，2016，（9）：34．

[9] 中华人民共和国教育部制定．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012．

[10] 柏毅，林娉婷．合作问题解决的概念建构——基于PISA2015 CPS的研究[J]．外国中小学教育，2016，（3）：52-56．

[11]  Ferguson C J. An Effect Size Primer: A Guide for Clinicians and Researchers [J]., 2009, 40(5): 532-538.

[责任编校：周学智]

Quantitatively Study of Mathematics Curriculum Standard under the Perspective of Cooperative Problem Solving——Based on 2015 PISA CPS Evaluation Framework

KONG Fan-zhe1, 2, ZHAO Na1, 2

(1. Experimental Center for National Basic Education, Jilin Changchun 130024, China;2. Faculty of Education of Northeast Normal University, Jilin Changchun 130024, China)

The intrinsic nature of mathematics course both required cooperative problem solving (that was CPS), and provided a natural carrier for its cultivation. According to evaluation framework of PISA2015 CPS, this paper aimed to build the evaluation index system to had a quantitatively research on curriculum standards in the view of the perspective of the CPS, and to analysis of the types and effects of CPS existing in curriculum standards. Study showed: Although(2011 edition) was promulgated before the issue of the CPS evaluation framework, but the connotation and requirements of the CPS had been infiltrated and presented well unconsciously, and the percentage of presentation had been to 35.38%, of which the present effect of the course objectives, 82 cases and implementation suggestion was best. And the mean of the present effect was on average richer in the course objectives, the amount of presentation was to 31.71% in 82 cases. At the same time, the amount of the CPS of 82 cases and implementation suggestion was consistent with that in the course objectives, and the standard conform to “big” (=0.38). Although(2011 edition) had realized the importance of the CPS and consciously cultivated the CPS, but still needed to further rationally think and be improved.

cooperative problem solving; mathematics curriculum standard; present; quantitatively analysis; PISA

G423

A

1004–9894（2017）03–0030–09

2017–01–21

国家社会科学基金“十二五”规划2012年度教育学重点课题——中小学理科教材难易程度国际比较（高中数学）（AHA120008）

孔凡哲（1965—），男，山东济宁人，国家基础教育实验中心副主任，东北师范大学二级教授，教育学博士，博士生导师，主要从事数学教育、课程与教学论、考试评价与学校管理研究．