数学基本活动经验主成分和层次水平划分研究

郭玉峰，张 芳



数学基本活动经验主成分和层次水平划分研究

郭玉峰1，张 芳1，2

（1．北京师范大学数学科学学院，北京 100875；2．浙江大学附属中学，浙江杭州 310000）

在文献分析和调查研究基础上，给出了数学基本活动经验构成要素的研究假设，通过自编测试卷进行题目测试，借助因素分析找出了数学基本活动经验的4个主成分，分别是归纳概括、类比推广、数学表达、证明；借助聚类分析得到数学基本活动经验的层次水平划分．

数学基本活动经验；主成分；层次水平划分

1 引 言

2014年教育部颁发了系列文件，全面深化课程改革、落实立德树人的根本任务[1]．其中一项重要举措是研究、制订学生发展核心素养体系，包括数学学科的核心素养．

学生数学核心素养的养成需要相应的知识储备、能力发展，尤其积累一定的数学基本活动经验，由此带动了一系列相关研究[2~4]．2011年义务教育数学课程标准正式提出数学基本活动经验的课程目标，得到数学家、数学教育研究者、中小学数学教师的广泛关注和肯定，数学基本活动经验研究日益成为关注的焦点和讨论的热点．就目前研究看，更多集中在如何认识数学基本活动经验及其与数学基础知识、数学基本思想、数学问题提出等的关系[5~7]、数学基本活动经验的分类及特点[8]、数学基本活动经验的教学策略[9]、信息技术与学生数学基本活动经验积累[10]，等等．有关数学基本活动经验的更深入研究，如数学基本活动经验构成的主成分分析及其层次水平划分的研究还较少，而这对一线教学和数学学科核心素养的深入探讨是非常重要的．

郭玉峰、史宁中在文[11~13]中已经系统阐述了为什么在义务教育数学课程标准中明确提出数学基本活动经验，数学基本活动经验的内涵和维度划分，针对初中学生的问卷测试结果给出了数学基本活动经验的不同层次水平划分等．这些研究在一定程度上刻画了数学基本活动经验的要素组成和层次水平，但维度划分的几个方面：观察联想、归纳猜想、数学表达、验证或证明主要基于文献分析和理论研究给出；层析水平划分是针对初中学生，结合文献分析给出的．如何进一步完善这些要素？这是要解决的主要问题．针对高中学生，拟在已有研究的基础上界定内涵、进行文献分析和一线教师调研，给出数学基本活动经验的维度划分假设，进行测试研究，通过因素分析研究数学基本活动经验的主成分、借助聚类分析研究数学基本活动经验层次水平划分，完善数学基本活动经验的量表．

2 研究设计和研究假设

2.1 研究设计

数学基本活动经验是一个复杂、内隐的心理品质，如何刻画其要素和水平划分是一件困难的事情．主要参考苏联心理学家克鲁捷茨基对中小学生数学能力的研究．因为能力是直接影响活动效率，并使活动顺利完成的个性心理品质[14]，这两者的研究方法有一定共通之处．克鲁切茨基于1955—1966年主要进行了数学能力的结构及其形成等研究．关于数学能力结构的研究主要分为以下几步：第一步：给出数学能力的成分假设．通过分析文献、数学家和物理学家的传记、观察对数学有天赋的儿童、分析中小学数学课程等，给出数学能力的成分假设；第二步：根据假设编制测试题对学生进行测试，用因素分析等统计方法给出数学能力的不同组成要素；第三步：根据题目特征、学生解题过程，对共同因素进行命名．此外，也参考了国内李洪玉，林崇德[15]、郭玉英[16]等研究中学生空间认知能力、物理思维能力结构成分的思路和方法．研究设计可用图1表示．

图1 研究设计框架

数学基本活动经验尽管是内隐的，但长期积淀后往往以某种习惯表现出来，如思维习惯、行为习惯、情感表现等．数学基本活动经验只针对学生的数学思维习惯，是学生长期经历数学思维活动过程中积累的数学思考问题的方式或思考问题的习惯．

2.2 研究假设

如同数学能力的研究，数学基本活动经验构成成分的假设基于两方面：分析数学家的创造过程；借助中学一线数学教师的调研．

2.2.1 数学家进行数学创造的思考过程

数学家进行数学创造时，会有怎样的思考习惯？一些数学家表示，他们在进行数学思考时经常会出现“顿悟”，百思不得其解的问题突然有了“答案”，这不是纯机遇，往往需要有意识的努力．也即，数学创造发明的过程需要经历准备、酝酿、顿悟、整理阶段[17]．准备阶段是努力进行有意识的数学思考，尽管往往以失败告终，但却为酝酿和顿悟阶段提供了条件．酝酿阶段是进行无意识的数学思考，“无意识不仅要担当起构造各种各样的思想组合的复杂任务，而且还要根据我们的审美原则去作最细微和最本质的选择”[17]．酝酿阶段是无意识将数学知识联系到一起，领悟最本质关系或拓展问题的过程．整理阶段是用符号等数学语言表达顿悟的结果并加以证明等，是有意识的数学思考过程．由此，数学家进行数学创造时往往经历：发现相距很近或很远事物间的联系（包括共性、特性和关系），寻找本质，用数学符号进行表达并证明结论．也即，这个过程一般可以表述为：准备（观察、分类比较、归纳概括、类比等）、酝酿（联想）、顿悟（领悟本质）、整理（数学表达、证明等）．

2.2.2 中学一线教师认为会数学思考的学生的特点

进一步调研、访谈了69名中学一线数学教师，请他们回答“会数学思考的学生的主要特点是什么？”，调研得到的主要结果见表1．

表1 调研的主要结果

2.2.3 数学基本活动经验构成成分的假设

基于以上，结合教学实践，学生积累数学基本活动经验很重要的方面是积累数学思维活动经验，即在经历数学思维活动的过程中，体验和感悟数学思考的过程，形成合理、正确的数学思考问题的方式或习惯．为此，数学基本活动经验构成成分的假设确定为：（1）观察；（2）比较；（3）数学表达；（4）归纳；（5）类比；（6）证明；（7）联想；（8）分类．

3 基于因素分析和聚类分析的数学基本活动经验研究

对以上8个研究假设，进一步编制测试题，通过因素分析寻求主成分，借助聚类分析给出层次水平划分．

3.1 编制测试题

测试问卷的研制经历了大半年的时间，期间查阅大量高中数学题、高考题和竞赛题，并和中学一线数学教师交流，不断调整，最终完成了编制工作．预测于2014年8月在安徽某省示范高中高三某班进行，预测问卷30份，测试时间2小时．根据预测结果，调整了2道得分非常低的题目、更换学生只凭记忆就能作答的一题，最终问卷有22题．8个研究假设对应的题目如表2．

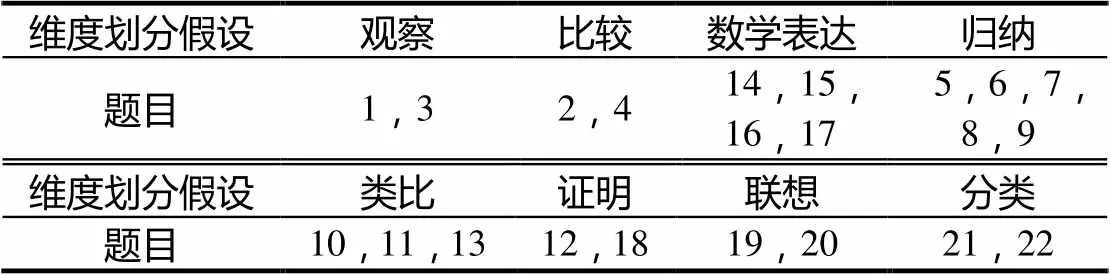
表2 研究假设及相应测试题目

3.2 测试的实施及问卷信与效度分析

正式测试集中在2014年9月，测试时间2小时．选取安徽、贵阳、唐山3所省级示范高中的高三年级，各省选取一个班．发放问卷138份，剔除空白卷，样本共计120人．

采用内容效度，利用SPSS软件，计算各研究假设得分与总分之间的相关性，如表3．

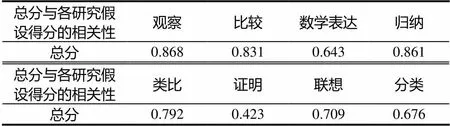
表3 各研究假设得分与总分的相关性

总分与各研究假设的得分之间均显著相关，试题具有良好的效度．

3.3 基于因素分析的数学基本活动经验主成分研究

对于8个基本假设，希望通过主成分分析，用更少一些不相关的指标代替具有一定相关关系的指标，同时又能尽可能多地反映原来指标的信息量[19]，即找出数学基本活动经验的主成分．首先，采用KMO和球形Barlett检验进行因子分析的适用性检验．用SPSS软件生成KMO和Bartlett球形检验表，见表4．

表4 KMO和Bartlett的检验

KMO检验测试值为0.826，说明各研究假设的信息重叠程度较高，可用因子分析模型进行降维[20]．检验样本分布的Barlett近似卡方值600.805，显著性水平=0.000<0.05，说明拒绝各变量独立的假设，即变量间有较强的相关关系，在5%的显著性水平下，测试数据适合进行因子分析．

其次，选择主成分法和旋转方法进行因素分析．用SPSS软件得到表5．

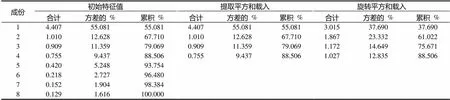
表5 解释的总方差

一般情况下，累计方差贡献率应达到85%以上，才能说明选取的因子基本包含全部指标的信息．这里，提取4个主成分时，解释率为88.506%，故选取4个主成分．进一步用SPSS软件分析，得到旋转成份矩阵，如表6所示．

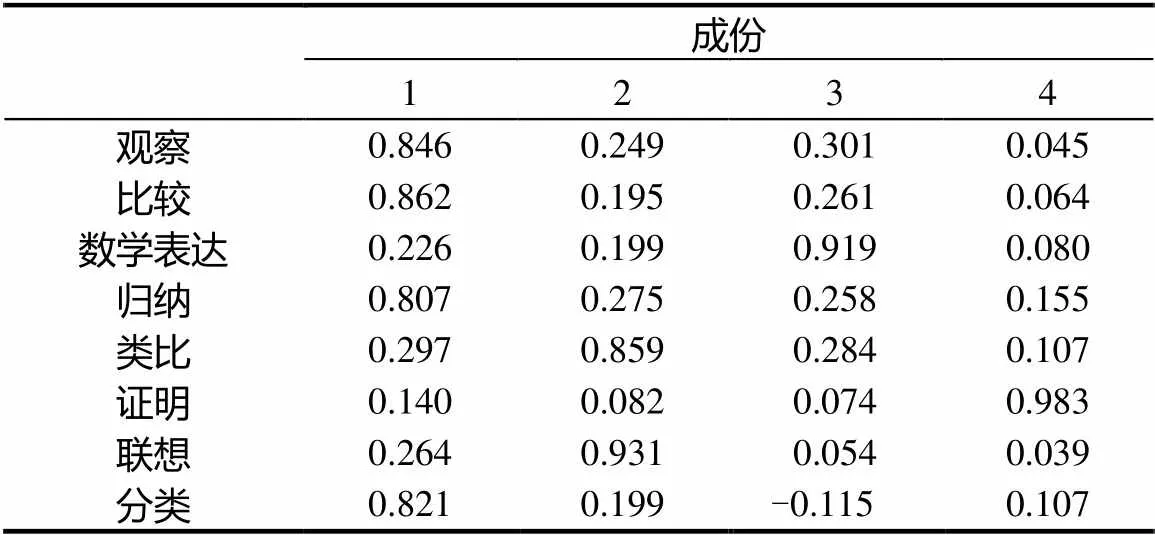
表6 旋转成份矩阵a

可见，4个主成分中，成分1与观察、比较、分类、归纳的载荷较大；成分2与类比、联想的载荷较大；成分3与数学表达的载荷较大；成分4与证明的载荷较大．

3.4 基于聚类分析的数学基本活动经验层次水平划分

下面根据学生的得分对学生进行聚类．将每个学生的总分、4个主成分的各自得分共5个数据作为聚类指标，进行分层聚类．利用SAS统计软件进行分析，得到的结果如表7．

表7 聚类表

表8 聚类结果

4 结论与讨论

4.1 研究结论

4.1.1 数学基本活动经验的主成分和各主成分的要素构成

研究只针对数学思维活动的经验．在分析数学家进行数学创造的过程和中学一线数学教师调研基础上，给出数学基本活动经验的8个成分研究假设，分别是观察、比较、分类、归纳、类比、联想、数学表达、证明．主成分分析显示，成分1与观察、比较、分类、归纳的载荷较大，命名成分1为归纳概括；成分2与类比、联想的载荷较大，命名成分2为类比推广；成分3与数学表达的载荷较大，命名成分3为数学表达；成分4与证明的载荷较大，命名成分4为证明．各成分的要素构成如下．

归纳概括是在观察的基础上对事物进行比较，进而将事物分类并由每类事物的特殊属性归纳其一般属性．其中，数学观察是对事物共性、特性、关系进行分析的过程；比较是确定研究对象的相同点和不同点；分类是根据研究对象的性质、找到合适的分类标准进而划归为不同类别；归纳是通过一类事物的部分对象具有某种属性，推知该类事物都具有这一属性．在观察、比较、分类和归纳基础上可以提出数学猜想．

类比推广是根据某类事物的属性而猜测在其它类的事物也可能存在相同或相似之处，进而引发思考并做相应的推广．归纳、类比、联想往往是有机结合在一起，但类比与归纳相比，需要更丰富的联想．

前两个成分主要是提出数学猜想，数学表达是用符号等数学语言表达数学猜想或其它结论．

数学猜想的结果是否成立需要借助数学证明．数学证明保证了由归纳或类比得到的一般命题的普遍有效性，是由命题的条件出发，根据与此相关的定义、公理、定理等，按照逻辑推理规则进行的逻辑推演．

这4个主成分反映数学思维活动的过程，是数学基本活动经验的因素构成．

4.1.2 数学基本活动经验的层次水平划分

聚类结果表明，数学基本活动经验的每个主成分都对应了3类学生，即每个主成分可以划分为3个层次．以下从每个类别中挑取个案来说明各层次特点：

关于归纳概括，学生得分由高到低依次为类别3、类别2、类别1，每个类别分别对应了归纳概括的层次1、层次2、层次3．每个层次学生的特点如表9．

表9 主成分1的不同层次特点

如测试题的第9题．该题的目的是：考察学生能否由特殊归纳一般，参考了波利亚《数学锻炼大脑——斯坦福大学数学试题与解答》．

原题为：如图2所示，第一层是一条与水平线垂直的线段，长度为1；第二层是在第一层的前端作2条与该线段成135°角的线段，长度为其一半；第三层按第二层的方法在每一线段的前端生成两条线段，长度为第二层的一半；重复前面的做法作图至第层．该树的第层的最高点至水平线的距离为第层的树形的高度．问：第层的高度是多少？请写出详细的计算过程．

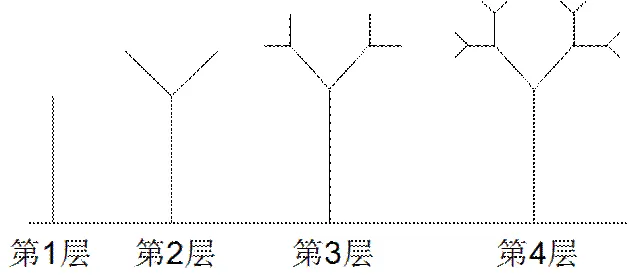
图2 测试题第9题图示

不同层次的学生对这道题有不同的解答．层次1的学生写出了第2、3层的高度，并且对进行分类，总结出了第层的高度；层次2的学生写出了第2、3层的高度，没有写出第层的高度；层次3的学生的答卷空白，他们表示对于这道题不知道如何下手，不知从特殊出发归纳一般．

关于类比推广，学生得分由高到低依次为类别3、类别1、类别2，每个类别分别对应了类比推广的层次1、层次2、层次3．每个层次学生的特点如表10．

表10 主成分2的不同层次特点

如测试题的第11题．该题的目的是：考察学生是否会类比猜想，即能否将等比数列中成立的结论类比到等差数列中，参考的是2013浙江镇海中学3月模拟卷的第17题．

不同层次的学生的答题情况不同．层次1和层次2的学生都知道等比类比到等差，积类比到和，商类比到差，层次1的学生写出的结果为，他们知道类比到等差，积类比到和，商类比到差．层次2的学生得出的结果是错误的，他们知道等比类比到等差，积类比到和，商类比到差，但是他们无法对类比后的结论进行调整；层次3的学生的答卷空白，他们不知道等比类比到等差，积类比到和，商类比到差，不能找到合适的类比对象．

关于数学表达，学生得分由高到低依次为类别3、类别2、类别1，每个类别分别对应了数学表达的层次1、层次2、层次3．每个层次学生的特点如表11．

表11 主成分3的不同层次特点

如测试题中的第17题．该题的目的是：考察学生能否会用符号语言进行数学表达，参考人民教育出版社A版数学必修教材．

原题为：将其转换成符号语言：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．

层次1的学生给出了正确答案，他们表示这道题十分简单；层次2的学生在进行数学表达时会漏掉题目中的关键信息，如“直线不在平面内”这个关键信息漏掉；层次3的学生不会用数学符号进行表达．

关于证明，学生得分由高到低依次为类别3、类别1、类别2，每个类别分别对应了证明的层次1、层次2、层次3．每个层次学生的特点如表12．

表12 主成分4的不同层次特点

如测试题中的第18题．该题改编自2013年北京高考理科数学卷的第19题，这道题要求学生先判断四边形的形状，再给出证明．其本质是一道证明题，因为学生很容易判断出不是菱形，进而此题就转化成了证明不是菱形，是一道证明题，其目的是：考察学生是否会进行演绎证明．

原题为：已知、、是椭圆上上的3个点，是坐标原点．若点不是的顶点时，四边形是否可能为菱形，说明理由．

不同层次的学生的答题情况不同．层次1的学生所用的方法合理，知道用反证法证明，证明过程都是对的，逻辑性强，思路清晰．层次2的学生知道用反证法进行证明，但是并没有得出最终结果．层次3的学生表示对于这样的题目无从下手．

4.2 讨 论

4.2.1 明确数学课程实施和教学实践中的关键环节

研究给出了数学基本活动经验的主成分：归纳概括、类比推广、数学表达、证明．这几个成分是学生数学创新能力培养的关键，是数学基本活动经验的4个关键因素．它们勾勒出了人们进行数学思维、包括数学的产生与发展过程中的关键环节，反映了科学的思考问题的方式．因而，有关数学基本活动经验主成分的定量分析，进一步明确了义务教育数学课程目标中提出的数学基本活动经验的构成要素，对于指导一线教师在实践教学中落实数学基本活动经验的课程目标提供了方向性指导．

数学教学中应该过程教学和结果教学相结合，然而，什么是过程教学？过程教学的结果是什么？对此是缺乏深入的理论探讨的．借助主成分分析，在研究假设基础上确定的数学基本活动经验的主成分，说明了数学过程教学的4个关键环节，同时，数学过程教学的结果之一是积累学生数学思考问题的方式或习惯，这是长期经历这4个关键环节后的结果．

4.2.2 明确数学基本活动经验各环节的不同层次水平

这里将数学基本经验的每个环节都划分成3个层次，每个层次的学生具有不同的特点，也代表了每个环节发展过程中所处的不同阶段．借助聚类分析得到的学生数学基本活动经验4个主成分的不同层次水平，可以帮助教师了解不同层次水平学生的表现和特征，有针对性地实施区别化教学，对于大面积提高数学教学质量也将是一个有益的启示．

4.2.3 推动学生数学核心素养研究的进展

尽管目前国内外对“何为数学素养”并没有统一的认识，关于数学核心素养的几个方面：抽象、推理、建模，以及运算、思维、空间想象等数学素养的具体内涵、构成要素等仍在研究、讨论中[21]．但是，比较一致的看法是数学学科核心素养的养成需要学生的知识储备、能力发展、经验积累．积累数学基本活动经验是数学素养养成的一个方面，对数学基本活动经验的主成分和层次水平的研究，进一步明确了从哪些关键方面积累学生数学基本活动经验，在这些关键方面学生的不同层次划分如何，这对研究数学核心素养，推动学生数学核心素养的养成无疑将起到巨大的推动作用．

[1] 中华人民共和国教育部．《教育部关于全面深化课程改革落实立德树人根本任务的意见》（教基二[2014]4号）[EB/OL]．http://www.moe.edu.cn/publicfiles/business/htmlfiles/moe/s7054/201404/167226.html

[2] 喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1-6．

[3] 郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1-5．

[4] 何小亚．学生“数学素养”指标的理论分析[J]．数学教育学报，2015，24（1）：13-19．

[5] 顾继玲．聚焦“基本数学活动经验”[J]．数学教育学报，2016，25（1）：34-37．

[6] 王新民，王富英，王亚熊．数学“四基”中“基本活动经验”的认识与思考[J]．数学教育学报，2008，17（3）：17-20．

[7] 宋运明．论数学问题提出和数学活动经验的关系[J]．数学教育学报，2010，19（6）：34-36，49．

[8] 张奠宙，竺仕芬，林永伟．“基本活动经验”的界定与分类[J]．数学通报，2008，（5）：4-7．

[9] 仲秀英．促进学生积累数学活动经验的教学策略[J]．数学教育学报，2010，19（5）：36-39．

[10] 徐章韬．超级画板：获取数学基本活动经验的优秀认知平台[J]．数学教育学报，2011，20（3）：97-99．

[11] 郭玉峰，史宁中．数学基本活动经验：提出、理解与实践[J]．中国教育学刊，2012，（4）：42-45．

[12] 郭玉峰，史宁中．“数学基本活动经验”研究：内涵与维度划分[J]．教育学报，2012，（5）：23-28．

[13] 郭玉峰，史宁中．初中学生基本数学活动经验的量化研究[J]．课程·教材·教法，2013，（11）：48-54．

[14] 克鲁捷茨基．中小学数学能力心理学[M]．上海：上海教育出版社，1987．

[15] 李洪玉，林崇德．中学生空间认知能力结构的研究[J]．心理科学，2005，（2）：269-271．

[16] 郭玉英．物理思维能力的因子分析模型及主因素研究[J]．北京师范大学学报（自然科学版），1988，（4）：107-111．

[17] 雅克·阿达玛．数学领域中的发明心理学[M]．大连：大连理工大学出版社，2008．

[18] 衷克定．SPSS for windows数据统计分析工具应用教程[M]．北京：北京师范大学出版社，2001．

[19] 高惠璇．实用统计方法与SAS系统[M]．北京：北京大学出版社，2001．

[20] 张红坡．SPSS统计分析实用宝典[M]．北京：清华大学出版社，2012．

[21] 周彦池，裴昌根．数学教育研究与实践的热点及趋势[J]．数学教育学报，2016，25（6）：93-95．

[责任编校：周学智]

Research on the Principal Component and Hierarchical Level Division of the Mathematical Activity Experience

GUO Yu-feng1, ZHANG Fang1, 2

(1. School of Mathematical Science, Beijing Normal University, Beijing 100875, China;2. The Affiliated High School of Zhejiang University, Zhejiang Hangzhou 310000, China)

The article investigated the integrant parts of students’ mathematical activity experience based on literature analysis and investigation. By factor analysis, four principle components were determined which were inductive generalization, analogy extension, mathematical expression, mathematical prove. By cluster analysis, hierarchical level diversion of mathematical activity experience were also determined. The research would prompt the implantations of curriculum objectives and core competences of mathematics.

mathematical activity experience; principal component; hierarchical level division

G420

A

1004–9894（2017）03–0025–05

2017–02–08

北京市教育科学“十二五”规划重点课题——“四基”之数学基本活动经验研究：量化与课堂实践（ABA12020）

郭玉峰（1972—），女，山东日照人，教授，博士生导师，主要从事数学课程与教材、数学学习心理研究．