小学数学教科书中“组合问题”的编排

刘晓燕，徐章韬



小学数学教科书中“组合问题”的编排

刘晓燕，徐章韬

（华中师范大学数学与统计学学院，湖北武汉 430079）

以人教版小学数学教科书中的“组合问题”为研究对象，从编排分布、素材选取、内容编写、呈现方式等4个方面进行研究．考虑到学生发展的阶段性，教科书采取了分散编排和集中编排相结合的形式；背景素材大多源于个体或群体的社会生活，而不是学科知识；在变式中体现中国教材“小步走”的理念；更多地采用图片、表格、连环画等方式．研究的结论：应精心选择组合素材，加强与传统成熟内容的关联，突出整体的观点；课程教材的改进、优化需要教师有责任担当；革新表述方式，使思想方法的渗透更自然，更切合小学生的心理特征．

组合问题；教材编写；心理特点

1 引 言

课程材料是知识的载体，课程材料的编写直接影响教师的教和学生的学．因此近几年来，对于数学教科书的研究逐渐引起了人们的重视．如，有的研究重点分析和讨论了数学教材研究的概念及所要研究的问题[1]；有的探索了新时期小学数学教材如何服务于教师的“教”和学生的“学”，真正发挥教材的“引导教学”的功能[2]；有的从HPM的角度对教材的编写作了对比研究[3]；还有的对人教版小学数学高年级教科书中的人物性别刻板插图进行了详细的统计和分析，视角十分独特[4]；更多的是一些国际教材的比较研究，例如具体对于某一年级、某一章节知识进行比较分析[5~6]．

课程标准指出：义务教育阶段的数学课程是培养公民素质的基础课程，具有基础性、普及性和发展性[7]．而小学阶段是学生认知水平和思维能力形成和发展的起始阶段，所以数学课程材料的选取显得十分重要．这个阶段的课程材料不仅应具有趣味性，还应能激发学生的“火热思考”．对于小学数学教材的研究，如通过研究西师版小学数学新教材，探析了中国小学数学新教材的编写特色[8]；有的从封面设计的角度对小学数学教材的编写特色进行了分析，想法新奇独特[9]；还有的从题材选取、呈现方式等方面研究了数学文化在小学数学新教材的选取及编排情况[10]．通过研究注意到小学教科书出现了很多令人欣慰的变化，小学数学教科书越来越重视以数学活动为载体，渗透数学的思想和方法，表现之一是越来越多的组合问题进入了课程材料．题材丰富，表述形式生动直观，富有趣味性，还涉及到分类、统筹、优化、建模等众多数学思想方法，对于学生思维能力的培养具有重要的教育价值．采取文本分析法，对人教版小学数学教科书的组合问题进行定量统计和定性分析，探讨组合问题在人教版教科书的编写特点，阐述选取课程材料、呈现课程材料时应思考的一些问题，以期更好地发展小学生的思维和学习热情，为人材的培养“从小抓起”提供参考．

2 编写特点

组合问题是指与离散对象有关的问题，指在一定的条件下对所要研究的离散数据进行安排或配置，主要是对象集合的计数或枚举，而不是方程、函数等涉及连续对象的问题．组合问题在计算机科学、编码和密码学、物理、化学、生物学等学科中均有重要应用．以人民教育出版社小学数学教科书中的“组合问题”为研究对象，以“编排分布、素材选取、内容编写、呈现方式”为分析框架，研究“组合问题”的编排特点．

2.1 编排分布

首先，统计教科书正文中有关组合问题的内容分布，结果见表1．从表1可以看到，组合问题贯穿小学数学学习的始终，以活动为载体呈现在教科书中，涉及到众多的数学思想和方法．

其次，统计教科书例题、练习题和总复习题中有关组合问题的内容分布．组合问题常与代数、几何等内容相交叉，彼此间又常相互渗透，难以对组合问题的类别进行准确的分类，以组合问题中涉及的主要因素为标准，将其分为分类问题、排列组合、数学化、组合几何、图论问题、组合优化、抽屉原理和逻辑推理8个大类，其中分类问题是按照某种条件对研究对象进行分类；数学化即数字编码、集合等问题；组合几何是对图形几何的拼搭、分割和排列问题；图论问题是将事物抽象成以点和边组合而成的几何问题；其他问题就不一一概述了．针对上述分类，对教材中的例题、练习题、复习题中涉及到的组合问题的题目数进行了年级分布统计，统计结果如表2．

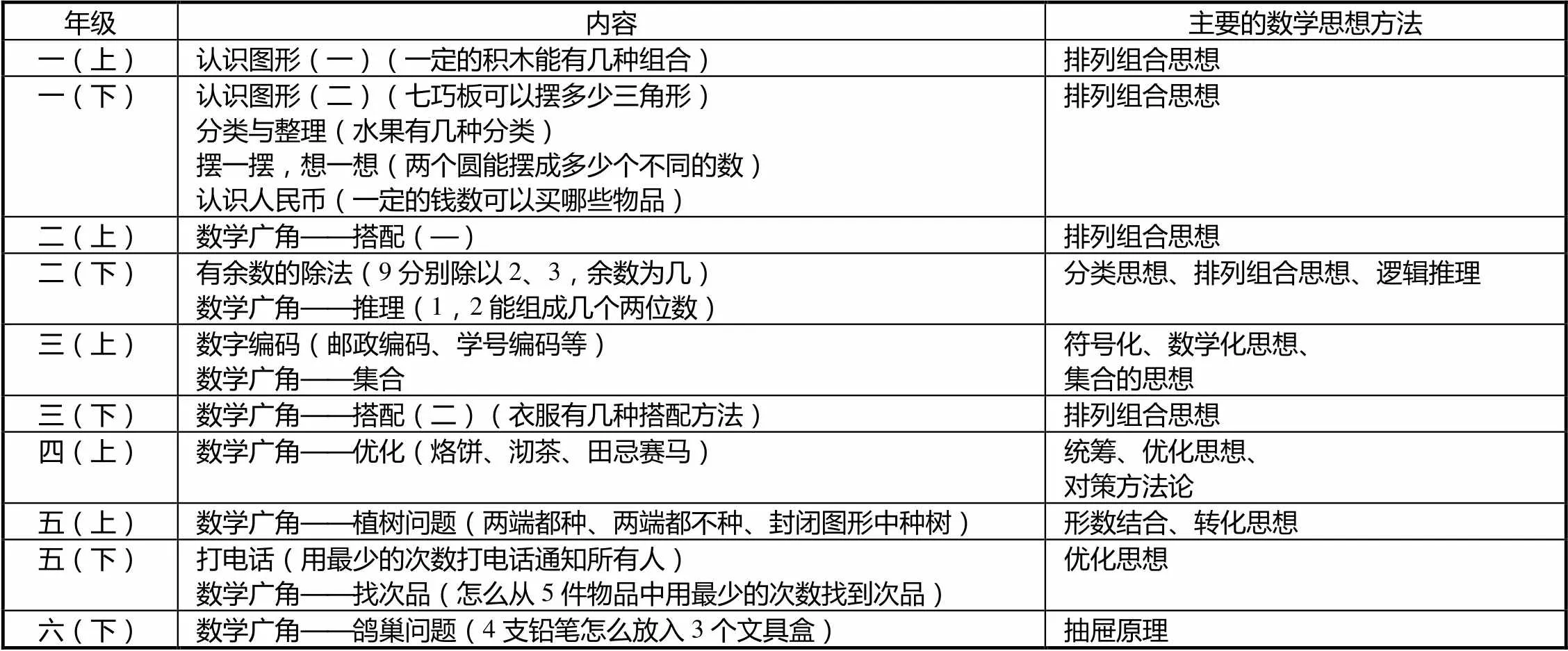
表1 组合问题内容编排分布

表2 组合问题所属领域统计

从统计结果可以看出，组合问题的编排具有分散编排和集中编排相结合的特点．其中，“分散编排”是将组合问题的内容渗透在代数、几何、统计中的题目中，如，以排列组合、组合几何和组合优化等问题为载体，为学生营造一个应用数学思想的平台，引导学生经历基于思考的学习过程．“集中编排”是指设置有关组合问题的专题，如“摆一摆、想一想”、“数学广角”等，在这些板块中体现某些典型的数学思想方法和解题策略，部分内容还具有综合性、应用性和实践性等特点，编排意图是以活动为载体，使学生在活动中获得数学活动的经验及数学的思想方法．

从统计结果可以看出，组合问题的编排考虑到学生发展的阶段性．不论是对于整体知识框架结构的设计，还是对某一知识内容的选择，大体上遵照学科的逻辑结构和学生的身心发展顺序，而对整套教科书的内容进行编排．在低年级阶段有数形结合、分类集合、有序思维、排列组合思想，这些都是一些比较基本和常见的思想方法，具有直观性的特点．到了高年级阶段，更侧重于如“七桥问题”、“鸽巢问题”、“植树问题”和“田忌赛马”等思维含量较高的问题，这些“类奥数”问题对于思考逻辑的缜密性要求较高，需要运用到列表、画图、转化等多种方法策略，并且解题方法具有多样性的特点[11]．小学生从低年级阶段的具体形象思维逐步过渡到高年级阶段的抽象逻辑思维，逐步完成思维深化升级，问题逻辑结构的发展与小学生的身心发展顺序相调协．

2.2 素材选取

组合的思想在生活、生产实际中无处不在．教科书中素材的选取来源于生活，有利于激发学生的学习兴趣，增强对思想方法的理解，充分领悟其数学价值与数学思想，优化人们的生活．根据所涉及到的背景素材，将教材中有关的组合问题分为群体生活、社会经验（密切联系学生的现实生活，如排队、购物等）、数学操作活动（主要指需要学生动手操作的活动和问题，如“摆一摆”、“画一画”等）、学科知识（没有任何背景的纯学科问题）4个类别，按年级统计的结果见图1．

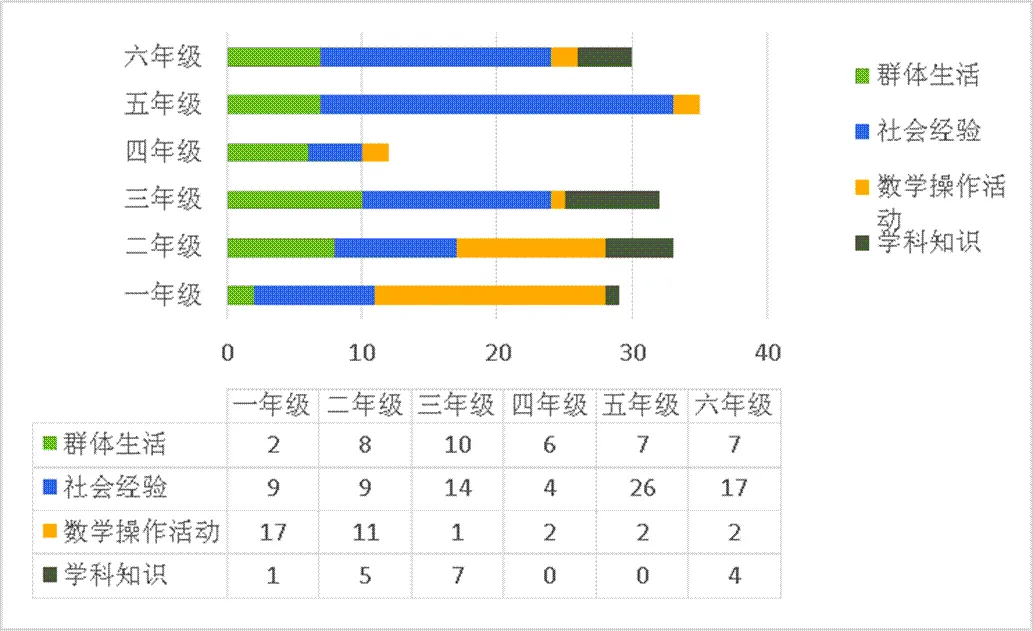
图1 组合问题素材选取年级分布

由图1可以看出，随着从低年级到高年级的发展，“数学操作活动”的素材逐渐减少，而关于个人“社会经验”的素材逐渐增多．低年级学段以“数学活动”为主要素材来源，因为这一阶段学生的思维主要以具体形象和动作思维为主，通过开展动手操作的探究活动能让他们直观地体验到现实生活中的组合问题．随着生活经验的丰富和视野的扩大，高年级学段的素材更多地以“社会经验”为主，如衣服搭配，学号登记等．这也表明教科书尊重了学生认知的发展，小学生最初通过身体体验引发心理状态的变化，逐步从自身认知走向社会认知．“群体生活”和“学科知识”变化不是很显著，“群体生活”的比例大于“学科知识”．

素材的背景取材于个体或群体的社会生活，而不是学科知识，表明教科书在处理数学与生活的关系上有明晰的观点——数学的源头在于生活，而且还落实了课程理念“课程内容的选择要贴近学生的实际，有利于学生体验与理解、思考与探索”．

2.3 内容编写

对于某一具体组合内容的编写，以二年级上册“数学广角——搭配（一）”为例，对内容编写进行分析．

这节课文由两道例题，3道变式习题，4道练习题组成．

例题一讨论的是用1、2和3能组成多少个十位数和个位数不同的两位数，这属于数码的排列组合问题．教科书通过两幅图来呈现学生探索、讨论问题的解决过程．第一幅图中女生和男生分别通过列图表和动手实践这两种不同的策略，解决了排列组合问题，体现出组合问题解决方法的多样性．“直观—操作”的解题方法，使学生体会到了排列组合的思想．第二幅图中点明“按规律排列”是解决问题的关键．第一幅仅涉及到两个数码，第二幅涉及3个数码，复杂性在增加，但第二幅图的解法可以化归到第一幅图中，体现了思维的渐近性．最后教材通过提出问题“怎样做才能不重不漏？”鼓励学生进一步思考，并安排一道习题进行巩固．“不重不漏”是解决排列组合问题的关键，有条理地思维才能保证突破这个关键点，而这也正是这则材料的教育价值所在．

例题二教科书也是以图片的方式来行文，通过两幅图来引导学生深入思考组合问题的特点——与顺序无关．接着通过安排“三人握手，共握几次”和“购物付钱的组合”这两道变式习题来加深对例题二的理解．总体上，例题二的思维含量高于例题一，问题逐步深入，体现了数学教学的层次性和组合问题自身逻辑结构的发展性．

最后，通过安排关于座位排列、书本排列、衣服搭配和币值组合的4道课后习题，引导学生运用已学的知识解决生活中常见的排列组合问题．并在单元小结中，点出有条理的思考问题和排列顺序的重要性，引发学生思考总结，回顾所学到的知识，并将其整理成一个完整的体系．

这节教材的编写，采用人物对白，图片展示的方式有层次地揭示组合问题的特点．在例题一中，可以看到有两个层次，先是局部地解决问题，然后把整体问题分解为局部问题，在男女生的对比中指出排列问题的要点．在例题二中，通过比较，让学生明白组合问题的要点，及与排列问题的区别．为什么先排列问题后组合问题，这是有道理的，排列问题要考虑次序，组合问题不考虑次序，在数学上是说条件在减弱，在思维上则不断予以自由．教材编写由例题到变式习题再到对应的训练习题，以及启发思考，提炼总结，一步一个脚印，均体现了中国教材“小步走”，拾级而上，结构严谨的特点．

2.4 呈现方式

教材的呈现方式对于学习兴趣的激发和学习效果的提升均有非常重要的影响．图片、表格、版式、色彩、人物形象、连环画还是阅读材料等，是教材给人的直接感受和视觉特征．认知心理学研究表明，视觉在儿童认识和记忆所学内容中的作用是很大的，如果能充分调动学生视觉的各个方面投入学习，那么学习效果将大大增强．因此，教科书应该根据小学生的认识水平和思维特征，更多地采用图片、表格、连环画等呈现方式，使内容更加直观形象，切合小学生的具体形象思维．纵观人教版小学数学教科书，组合问题的呈现方式分为纯文字和图文结合两种，图文结合又可分为表格、连环画、卡通人物和情境图片（图片的内容为问题中的关键词或所处的情境），统计结果见表3．

表3 组合问题呈现方式年级分布

从页面版式看，每页大约3~4个题目，并且所配插图提供的情境具有故事性和连续性；画面色彩鲜艳、图文并茂；选择的材料注重趣味性和直观性，如各种各样的动物，五颜六色的七巧板，等等．从画面的呈现方式来看，教科书采用了文字、图表、卡通图片等丰富多彩的形式．其中绝大部分为图文结合，而情境图片更为主要形式，表格、连环画、卡通人物和纯文字的比例较少．随着年级的升高，纯文字的呈现方式逐渐增加，情境图片的数量则在相应地减少．这样的呈现方式一方面符合小学生年龄和认知特点，另一方面对于组合问题本身而言，也体现出了随着组合问题思维的不断深入，其表达方式经历了从图形直观到语言描述的逐步过渡和发展．在语言方面，考虑到学生的认知水平和思维基础，文本语言大都简单明了，直截了当，多以对话为主，如在五年级上册植树问题中，男生说：“每隔5 m栽一棵，共栽100÷5=20（棵）．”女生回答：“对吗？检验一下．”小天使提示：“100 m太长了，可以先用简单的数试试．”另一个女生回答：“我先看看20 m可以栽几棵．”通过人物间的对话，体现出解决问题的过程和解法的多样性．

在总体布局方面，先是例题引入、正文，然后是相应的变式训练习题和复习题巩固知识，最后是单元小结总结重点．部分单元最后还设置了“你知道吗？”、“数学游戏”等阅读材料补充相应的课外知识，扩大学生的视野和知识面．

3 讨论与分析

根据前面的研究结果，可以认为，人教版小学数学教科书对于组合问题的编写整体上符合学生的认识规律和身心发展水平，是教科书中非常具有特色的组成部分．但是仍有问题值得讨论与分析，使之更好地促进学生的发展．

应精心选择组合素材，并加强与传统成熟内容的关联．虽然，组合问题中蕴含着丰量的数学原理和思想方法，如分类、对应、转化、优化、数形结合、数学建模、逻辑推理等，这些数学思想方法对于发展学生的思维与认知有很高的教育价值．通过组合问题的学习，能培养学生分析、综合、比较、抽象、概括、归纳、演绎等思维能力，掌握解决问题的基本方法．而且，教科书的编写者的确有此意图[12]．但是，应注意到，组合问题是以“数学广角”的形式出现在教科书每一章的末尾，不是教科书的主干内容，不以传授知识为主要目的，与前面成熟的传统内容没有多大的关联，这样做似乎不太合适．以取食为例，知识犹如各种食材，如大米、菜蔬、鲜肉等，思想犹如各种营养元素，如蛋白质、维生素及各种微量元素等．人体为了保持健康，不会专门去吃各种营养元素，而是从食材中获取各种营养元素．思想方法的教学应和小学数学的传统成熟内容建立关联，这样做有诸多好处．比如，“田忌赛马”、“沏茶”、“烙饼”指的是生活中的一种优化思想，不学数学的人同样也能获得这些思想．出现在数学教科书中的优化思想的教育意图何在，是广大研究者应该深入思考的问题．优化的思想无处不在，生活中有数学，数学中也有，与小学数学的传统成熟内容密切相关的优化思想可以体现在简便计算及各种算法、算理的分析上．这样，优化就从生活走向了数学；从数学的角度对优化进行深入的分析，形成一门学问，提出各种优化对策来解决生活中的各种问题，数学又走向了生活．在“生活—数学—生活”的循环圈中，组合问题便固着在了数学知识的载体之上，不再简单的是一种游戏．又如，各种游戏对策问题可与带余除法，等差数列等内容发生巧妙的关联，如果组合问题与这些传统成熟内容关联起来，组合数学就在教科书中扎稳了根．

与传统成熟内容发生关联，还要有整体观．中小学数学的学习应有一个整体规划．小学教科书中的“数学广角”的问题，几乎就是组合数学问题．可以简单地分成5类．（1）与围绕集合而展开的内容．如，集合的构造（分类就是一种构造集合的方法）、集合的计数（加法原理、乘法原理和容斥原理）、简易逻辑（集合间关系的探讨），等等．（2）各种关系的探讨．如，对应、枚举、归纳、递推、方程、函数、构造，等等．（3）各种数学化方法．如，染色赋值、图论建模，等等．（4）各种数学手段的研究．如，极端原理、抽屉原理、奇偶分析、对称补形、有序化，等等．（5）典型数学问题．如，游戏对策、等周问题、一笔画问题、形数问题、凸集凸包，等等．对于这些思想方法在中小学课程教材中的分布，应有一个整体的考虑．这些思想方法会在后续课程中出现吗，何时出现；如果这些思想方法在后续课程中还会出现，那么在小学阶段应如何把握教材的深度．这些思想方法在高中数学教材中大都会出现，而在初中数学教材中出现得很少或根本不出现．思想方法的熏陶应是一个长期的一线串通的过程，出现断裂带不好．如，图论的观点和方法可以作为一种数学建模的手段来用，可以用来刻画有丰富内在关系的对象组，可以认为是对图形或几何采取了不同于欧氏几何的观点和方法．可以和平面几何的学习建立关联，如从图论的角度寻找辅助线，沟通点与点之间的关联．这样，图论的观点和方法，从小学的“七桥问题”游戏，经初中的图论观点下的辅助线，到高中的欧拉公式，形成一条或明或暗的学习线，不至于被割裂．思想方法的熏陶是一个渐进的长期过程，应具有层次性．如，“打电话”中出现了递推的思想，对小学生就显得有点难了，而且这还是一种极其理想的情况“谁被通知谁没有被通知，打电话的人都是清楚的”；如果一定要渗透递推的思想可以考虑如何和高中的数列发生关联，如何选择承载递推思想的素材．思想方法的熏陶是一个反反复复的过程，应有不同程度的变式．如，分类、计数、对应、枚举、归纳、符号化等思想方法在小学可以渗透，在初中也可以渗透，在高中亦然，而学生对象的心理特征、思维层次在不断地变化，承载思想的素材如何适应学生就是一个需要认真考虑的问题．如，不能讲到枚举、归纳，小学是“找次品”，初中、高中还是“找次品”，一定要注意素材的多样性．

课程教材的不断改进、优化需要教师有责任担当．显然，课程标准及教科书的编写者的意图都是良好的，希望通过“数学广角”这一板块开发学生的智能，让学生在动手操作、动脑思考、合作交流的过程中真正理解和掌握基本的数学知识和技能、数学思想和方法，获得广泛的数学活动经验，然而，课堂教学依然是学生身心发展的主要场所，没有教师的主动性和积极性，这部分内容很难收到期望的效果．另外，这部分内容与小学数学的传统内容关联不是很大，是一些“类奥数”的问题．“奥数”的名声并不好，其中最要害之处在于许多人用之牟利．但不可否认，这些“类奥数”问题有着鲜明的育人价值．这就要求教师要有责任有担当，充分发挥课堂教学这块主阵地的作用，紧密结合传统内容，充分挖掘“类奥数”问题的思维价值和教育价值，把学生紧紧地凝聚在学校教育的周围．那种“课堂上不讲，课后找学生补课”的做法，就是把学生往培训机构推，教师之道尽丧矣．

革新表述方式，使思想方法的渗透更自然，更切合小学生的心理特征．“数学广角”在很多方面考虑了小学生的心理特点，如，素材（载体）贴近学生的生活经验，教材的视觉呈现方式考虑了小学生的兴趣爱好，等等．这些方面还可多做些尝试．思想方法其实是一种道理．讲道理，不一定要采取论证、议论的方式，也可把道理寓于形象之中，用形象也可说理．人们可以通过读各种史料、史论了解国家、社会的变迁规律，也可以通过读各种形象的文学作品，了解社会的运作规律．考虑到小学生的年龄特点和审美情趣，为了吸引小学生的注意力，可采用直观、简洁、清晰的图表呈现信息，使之一目了然；可采用具有故事性和连续性的连环画，吸引小学生的注意力和兴趣，讲好数学故事，学好故事中的数学．

[1] 范良火，熊斌，李秋节．现代数学教育中的教材研究：“概念”“问题”和“方法”[J]．数学教育学报，2016，25（5）：1-4．

[2] 李星云．引教导学：对小学数学教材建设的思考[J]．课程·教材·教法，2006，（12）：42-45．

[3] 徐章韬，梅全雄．HPM视角下的数学教材编写[J]．数学教育学报，2009，18（3）：14-17．

[4] 魏佳．小学数学教科书性别刻板插图的调查与思考：教科书发展的视角——以人教版小学数学高年级教科书为例[J]．数学教育学报，2015，24（5）：96-99．

[5] 丁锐，Yan Ping Xin．中美小学数学教材的比较研究——以三年级“分数的认识”为例[J]．数学教育学报，2016，25（3）：20-28．

[6] 王建波，曹一鸣．中美澳初中数学教材统计内容比较研究[J]．数学教育学报，2016，25（3）：14-19．

[7] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012．

[8] 李欣莲，宋运明，张渝．小学数学新教材编写特色再探——以西师版为例[J]．数学教育学报，2014，23（2）：89-92．

[9] 张辉蓉，俞向军．小学数学教材封面设计的探索及思考——以西师版小学数学课标教材为例[J]．数学教育学报，2014，23（3）：83-86．

[10] 孟梦，杨慧娟，李长毅．数学文化在小学数学新教材中的实践研究——以西师版为例[J]．数学教育学报，2012，21（2）：61-63．

[11] 季璇，徐章韬．适度把握小学数学教材中的“类奥数”问题[J]．湖南教育，2013，（3）：26-28．

[12] 熊华．加强数学思想渗透 发展数学思维能力——对人教版小学数学教材“数学广角”修订的几点思考[J]．课程·教材·教法，2011，（9）：61-66．

[责任编校：周学智]

Arrangement of Combination Problems in the Primary School Mathematics Textbook

LIU Xiao-yan, XU Zhang-tao

(College of Mathematics and Statistics, Central China Normal University, Hubei Wuhan 430079, China)

This paper focuses on the study of the combination problems in the elementary school mathematics textbook, and studies from four aspects: arrangement distribution, material selection, content preparation and presentation mode. The results show that considering the stages in the development of students, decentralized arrangement and centralized arrangement combination; Rather than knowledge, background material mostly from individuals or groups of social life; In the variant reflects our textbook “step away” concept; Presentation more with pictures, tables, comic books. We should carefully choose the combination of material, strengthen the association with the traditional mature content and highlighting the overall point of view; The improvement and optimization of the course materials require teachers to have the responsibility to play; Reform expression, make the method more natural and suitable for the pupils’ psychology characteristics.

combination problems; the arrangement of textbooks; psychology characteristics

G622

A

1004–9894（2017）03–0068–05

2017–01–16

华中师范大学重大科研课题及创新示范基地培育项目——TPACK视角下卓越数字化教师的培养研究（CCNUE2015-5）；湖北省高等学校省级教学研究项目——卓越数字化教师培养的路径和条件分析——以数学教师为例（2015095）

刘晓燕（1994—），女，山东潍坊人，研究生，主要从事数学的教与学研究．