数学高考中实践应用能力考查研究

陈 昂，任子朝



数学高考中实践应用能力考查研究

陈 昂，任子朝

（教育部考试中心，北京 100084）

实践应用能力是数学学科的一个重要能力，近年来的高考试题加强了对实践应用能力的考查，体现了数学在解决实际问题中的巨大威力和应用价值．实践应用能力的考查过程分为以下几个阶段：表征分析阶段，提炼数量关系阶段，数学建模阶段．高考试题根据不同阶段的特点，设置了不同的考查方法．

高考；实践能力；应用能力；数学建模

1 引 言

进入新世纪后，为进一步增强本国的竞争实力，提升人才培养的素质，世界各发达国家已竞相开展对学生素养的相关研究．中国的《国家中长期教育改革和发展规划纲要（2010—2020年）》（以下简称《纲要》）中明确提出了将“坚持以人为本、推进素质教育”作为教育改革发展的战略主题．其中重点是面向全体学生、促进学生全面发展，着力提高学生服务国家和人民的社会责任感、勇于探索的创新精神和善于解决问题的实践能力[1]．近年来，为落实《纲要》精神，数学科高考在实践应用能力的考查上进行了积极的探索和实践．

数学是研究数量关系和空间形式的科学．数学与人类生活和社会发展紧密关联[2]．这种联系是双向的，一方面，数学的发展依赖于社会环境，受社会经济、政治、文化等诸多因素的影响；另一方面，数学的发展又反过来对人类社会的进步起到推动作用，包括对人类物质文明和精神文明两大方面的影响[3]．20世纪以来，数学向社会、经济和自然界各个领域的渗透，扩展了数学与实际的接触面．数学科学应用于经济建设、社会发展和日常生活的范围和方式发生了深刻的变化[4]．数学在搜索引擎、人工智能、大数据分析等中的应用已经改变了人们的生活．近年来的高考数学试题紧密结合社会实际和考生的现实生活，加强对实践应用能力的考查，体现了数学在解决实际问题中的巨大威力和应用价值，体现了教育改革中加强实践性、应用性的要求．

2 实践应用能力的考查方法

数学科实践应用能力是指学生主动参与和体验数学知识发生和发展过程，并运用数学知识、思想和方法对实际问题进行分析研究，并解决问题的能力．在考查过程中，可以将实践应用能力的考查分为以下几个阶段：表征分析阶段，提炼数量关系阶段，数学建模阶段．在实际命题过程中，根据不同阶段的特点，研究制定不同的考查方法．

2.1 表征分析阶段

表征一般分为外部表征与内部表征，文中的表征指的是外部表征，指的是用一种形式将事物特征、关系、知识重新表现出来，试题背景、设问的呈现方式等是表征的基本信息条件．表征分析是实践应用能力考查的基础阶段，美国现代认知心理学家西蒙认为：“表征是问题解决的一个中心环节，它说明问题在头脑中是如何表现出来的．”[5]在表征分析阶段，可以提供多样化的信息，例如表格、图形等，要求考生能够正确理解题意，能够将生活中的文字、图表转化为数学语言和数学关系．

2.2 提炼数量关系阶段

提炼数量关系是指通过实践探究，让考生通过内心体验、思维活动、操作过程，独立思考，自主探索，发挥主观能动性，研究问题的本质．数学家欧拉说过：“数学这门学科，需要观察，还需要实验．”[6]通过实验可以忽略次要因素，突出主要因素，为接下来解决问题提供帮助．提炼数量关系是实践应用能力考查的主要阶段，在这个阶段可以让考生感受数学知识发展、形成的过程，让其从实践中发现和总结形成结论，从特殊到一般地进行归纳总结，从具体到抽象进行升华．对提炼数量关系阶段考查时，可以让学生主动参与和体验知识的发生和发展过程，让他们亲自体验数学概念，数学产生的实际背景和形成的过程，考查其思维过程和思维方法．

2.3 模型化阶段

模型化是指从现实问题中运用数学思想、方法和知识建立数学模型解决实际问题的过程．数学模型是应用数学知识解决实际问题的一种有效的工具，是对现实对象的信息通过提炼、分析、归纳、翻译的结果，它使用数学语言准确地表达了对象的内在特征．模型化是实践应用能力考查的高级阶段，在对这一阶段进行考查时，需要经历从实际问题出发，到建立模型，检验模型以及使用模型的全过程．其流程如图1所示．

图1 数学建模过程

3 高考中对实践应用能力的考查

实践探究能力主要在应用题中进行考查，从1993年高考中注重考查数学应用题以来，经过多年的摸索，近年来高考进一步加强应用题的考查．与此同时，实践应用能力的考查形式有所突破和创新．

3.1 对表征分析的考查

解决一道数学应用题，首先需要读题，理解题中的数字、变量名和关系这些基本因素，这就是表征的开始[7]．试题对表征分析的考查主要体现在两个方面，一个是要求考生利用表征信息分析问题，解决问题，另一方面则是利用图象、表格等多种表征信息提供基础信息和背景条件，要求考生可以从不同表征信息中研究问题，从而实现考查目的．

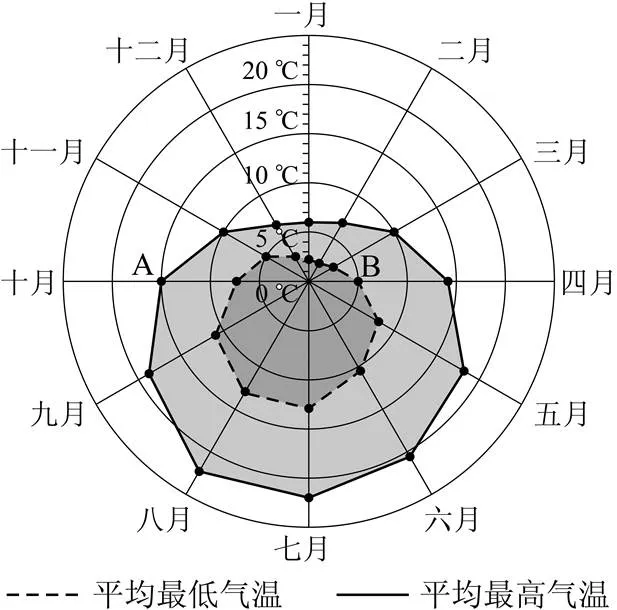
例1 某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图．图中点表示十月的平均最高气温约为15°C，点表示四月的平均最低气温约为5°C．下面叙述不正确的是（ ）

（A）各月的平均最低气温都在0°C以上

（B）七月的平均温差比一月的平均温差大

（C）三月和十一月的平均最高气温基本相同

（D）平均最高气温高于20°C的月份有5个

试题设计的实际背景源于生活，为考生所熟悉，试题表征是通过给出一种课本中没有介绍的新的统计图——雷达图，并加以适当说明，要求考生读懂统计图的内容．通过这样的设计要求考生通过读图、识图，对表征进行分析，从而得出结论．

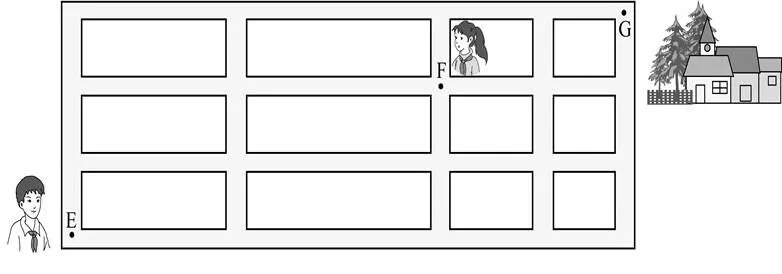
例2 如图，小明从街道的处出发，到处与小红会合，一起到位于处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（ ）

（A）24

（B）18

（C）12

（D）9

试题从考生熟悉的真实生活情境出发，设计一个利用分步乘法计数原理进行计数的试题，主要考查考生对基本计数原理的理解和掌握程度以及应用能力．试题背景是日常生活中常常遇到的最短距离问题，在表述这类问题时，运用自然语言或者数学语言对背景材料表述清晰往往较为繁琐，而通过引入图象表征，准确清晰地表述出最短距离的实际背景，实现了考查目的．

3.2 对提炼数量关系的考查

数量关系的提炼是在考生对试题表征分析后，考生对问题进行分析、加工提炼的过程．在这一过程中，考生选取的理论依据直接决定了问题解决的顺利与否．因此，在对提炼数量关系进行考查时，要求考生挖掘题目内涵，选取适当的方法策略，思维路径等，对考生解题中的过程与方法提出了要求．

例3 某公司计划购买2台机器，该种机器使用3年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在3年使用期内更换的易损零件数，得下面柱状图：

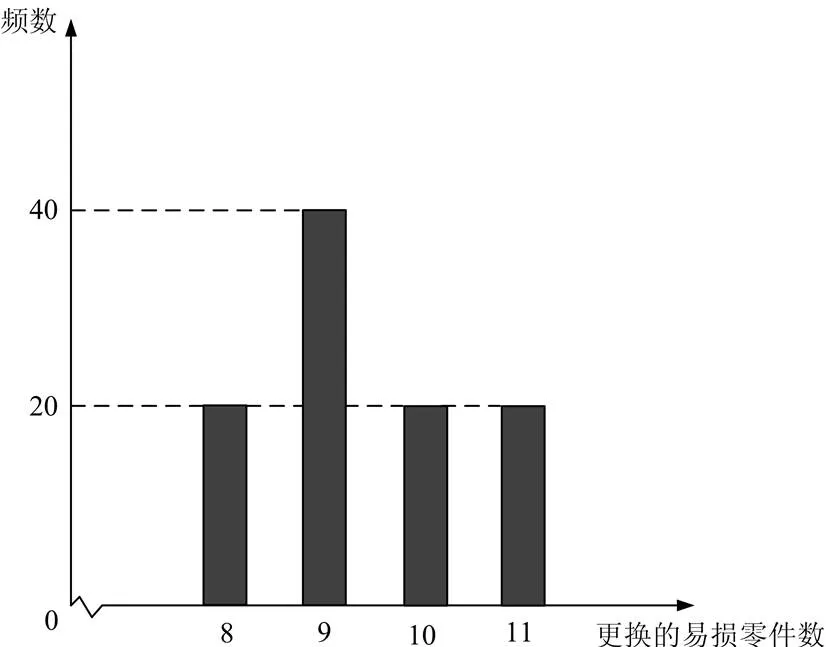
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记表示2台机器3年内共需更换的易损零件数，表示购买2台机器的同时购买的易损零件数．

（Ⅰ）求的分布列；

（Ⅱ）若要求(≤)≥0.5，确定的最小值；

（Ⅲ）以购买易损零件所需费用的期望值为决策依据，在=19与=20之中选其一，应选用哪个？

试题以企业的成本控制问题为背景，着眼于“最优化零部件采购量”的决策问题设计和设问．由于需更换的易损零件数具有不确定性，因此需要建立随机模型并应用统计与概率的知识确定最优的备件购买量．为解决此问题，需要先分析易损零件数的不确定性，即确定或近似确定易损零件数的分布列，这就是试题的第（I）问；第（Ⅱ）问在此基础上，对概率进行了考查；第（Ⅲ）问则需计算=19与=20时所需费用的期望值，为此首先需要清楚在给定的情况下所需费用与2台机器共需更换的易损零件数之间的关系，再结合的分布列得到的分布列，在此基础上可容易地求出所需费用的期望值．通过这样的设计使学生体会数学、统计与概率知识与现实生活息息相关，同时也引导考生思考，研究数量之间的关系．

3.3 对数学建模的考查

通过建立数学模型，解决实际问题是高考考试要求的重要内容．特别是伴随着大数据时代的到来，人们常常需要对网络、文本、声音、图象等大量信息进行数字化处理，使数学模型的研究领域与应用领域得到极大拓展，特别是随着统计与概率知识在中学数学教学内容的增加，为学生数学建模的提供了知识储备和解题工具．在对其考查时，可以从模型建立、检验模型等方面设置问题．在对数学建模考查时，更为注重根据题干中的精确数据构建数学模型，强调用数学知识、思想方法解决数学问题的能力，淡化对数据的分析和处理．

例4 某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5 kg，乙材料1 kg，用5个工时；生产一件产品B需要甲材料0.5 kg，乙材料0.3 kg，用3个工时．生产一件产品A的利润为2 100元，生产一件产品B的利润为900元．该企业现有甲材料150 kg，乙材料90 kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为元．

该题的背景是企业的生产安排问题．企业的利润受到材料数量和工时的限制，所以该题的本质是带有约束条件的线性规划问题．考生可以根据已知条件很容易地建立模型．但值得注意的是，考生所建立的数学模型还需要进行实际检验，假设生产产品A和产品B的数量分别为和，则除了该题关于和的明显给出的约束条件：甲材料和乙材料的数量以及工时限制之外，还有自然约束条件≥0和≥0．在这样的约束条件下考生求出的解才是符合实际生产的结论．

例5 某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费（单位：千元）对年销售量（单位：t）和年利润（单位：千元）的影响．对近8年的年宣传费和年销售量（=1, 2,…, 8）数据作了初步处理，得到下面的散点图及一些统计量的值．

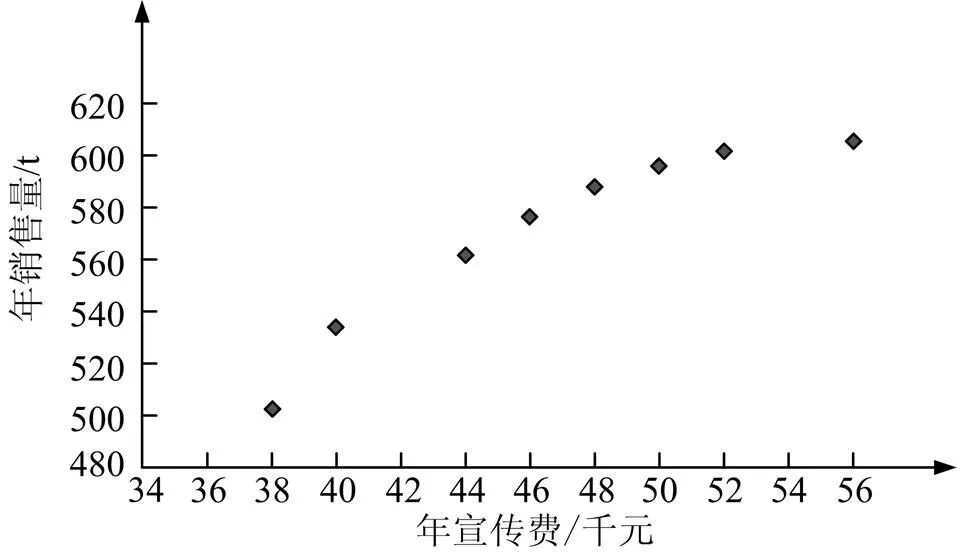
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立关于的回归方程．

（Ⅲ）已知这种产品的年利润与、的关系为．根据（Ⅱ）的结果回答下列问题：

试题以公司的财务管理为背景，首先给出了某公司年销售量和年宣传费的散点图，旨在考查考生通过统计图进行数据分析的能力．考生需要通过观察，对两个变量之间的相关关系做出直观判断．与常见题型不同的是，该题重点考查数学模型建立的选择，从散点图可以看出，样本点并没有分布在某个带状区域内，由此可以初步排除线性回归模型．在此基础上，考生需要借助线性回归模型系数的最小二乘估计来建立年销售量与年宣传费之间的非线性回归方程，从而确定年利润预报值与年宣传费之间的关系，最终通过求二次函数的最值得到利润的最大预报值．试题的设计有利于培养学生的数学应用意识，考生领会到统计与概率的思想方法在现实生活和公司经营等领域中有着广泛应用，形成自觉应用数学知识指导社会实践的意识，提高学生的综合实践能力．

4 启 示

弗赖登塔尔曾经说过：“应从两个方面来理解数学应用，即要重视从实际问题中提取数学概念与原理，又要重视用数学概念与原理反过来处理实际问题．”[8]实践应用能力考查的一个重要目标是让考生体会数学与现实世界的联系，树立正确的数学观．一方面，使学生体会数学的实践价值和应用价值，拉近数学与实际生活的距离，另一方面，由于试题的素材结合了实际背景，更直观地体现数学学科中的人文精神与德育价值．

数学教育在传授学生数学知识的同时，更要注重数学文化的教育和熏陶，培养和提高他们的数学素养[9]．随着新一轮课程改革的推进，数学科将不再分文理科教学，而且进一步明确了高中数学科核心素养．数学科核心素养是数学课程目标的集中体现，是学生在数学学习的过程中逐步形成的．数学科核心素养包含具有数学基本特征的思维品格和相关能力，包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析．这些数学素养都能与数学应用相互联系，尤其是数学建模更是应用能力重点考查的部分．今后的高考数学科要研究不分文理科后数学学科的考试目标、能力要求、内容范围、命题方式、试卷结构．突出数学的基础性、综合型、应用性和创新性，满足高校各专业对考生数学基础知识和数学能力的要求，因此对应用能力的考查应当与时俱进．

高考加强对实践应用能力的考查，有利于引导中学教育联系实际，创设有助于学生自主学习的问题情境，引导学生通过实践、思考、探索、交流来获得知识、形成技能，发展思维、学会学习．高考为高校录取合格新生提供依据，而对大学生的一些研究表明，大学生在解决简单应用题时，仍需要构建情境模型[10]．因此，在高考对实践应用能力的考查应设置具有挑战性的问题情境．这样将有利于对考生的甄别，激发学生进行思考．同时在设问时提出有一定跨度的问题引导学生进行自主探索，动手实验，使学生在探索过程中进一步理解所学的数学知识，掌握解决实际问题的方法，增强解决问题的能力．

[1] 国家中长期教育改革和发展规划纲要（2010—2020年）[EB/OL]. http://www.moe.edu.cn/publicfiles/business/ htmlfiles/moe/moe_838/201008/93704.html.

[2] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003．

[3] 李文林．数学史概论[M]．北京：高等教育出版社，2002．

[4] 刘来福．数学模型与数学建模[M]．北京：北京师范大学出版社，2009．

[5] 胥兴春，刘电芝．问题表征方式与数学问题解决的研究[J]．心理科学进展，2002，（3）：264-269．

[6] 徐利治．数学方法论选讲[M]．武汉：华中工学院出版社，1988．

[7] 邢强，单永明．数学应用题外部表征的影响因素及启发[J]．数学教育学报，2012，21（5）：19-22．

[8] 弗拉维尔，米勒．认知发展[M]．邓赐平，刘明译．上海：华东师范大学出版社，2002．

[9] 朱长江，李书刚，胡中波．在数学文化课程中引进优质教学资源开展混合式教学的探索与实践[J]．数学教育学报，2016，25（4）：30-32．

[10] 李晓东，付馨晨，鲁成．冲突情境对大学生解决简单应用题的影响：一项眼动研究[J]．数学教育学报，2016，25（4）：94-97．

[责任编校：周学智]

Study on the Testing of Practical Ability in College Entrance Examination

CHEN Ang, REN Zi-zhao

(National Education Examinations Authority, Beijing 100084, China)

Applying ability was an important ability in mathematics, recently, college entrance examination began to strengthen the test of applying ability, reflecting the role of mathematics in solving practical problems and application value. Mathematics application ability test process was divided into the following stages: analysis phase, Refine the number of relationships, mathematical modeling stage. According to the characteristics of the different stages, we set different test methods.

college entrance examination; practical ability; application ability; mathematical modeling

G420

A

1004–9894（2017）03–0015–04

2017–02–05

全国教育科学规划单位资助教育部规划课题——高考国家题库建设研究（FCB160610）

陈昂（1983—），男，湖南长沙人，助理研究员，主要从事数学教育和教育测量研究．