基于试验结果的碰撞前车速误差的校正∗

张 健，梁 超，高金贵，丁同强，李 江

基于试验结果的碰撞前车速误差的校正∗

张 健1，梁 超1，高金贵1，丁同强2，李 江2

(1.北华大学汽车与建筑工程学院，吉林 132013； 2.吉林大学交通学院，长春 130022)

为控制基于典型汽车碰撞模型计算的碰撞前车速误差，采用了反推算法。对2起车辆碰撞事例进行了碰撞前车速的模拟和试验。模拟结果表明，碰撞后车速误差是影响模型计算的碰撞前车速准确性的关键因素，而相对而言力学参数误差的影响则小得多。以碰撞试验结果为准确值对模拟计算的碰撞前车速误差进行了不同校正的研究。结果表明，对碰撞后车速误差和力学参数误差进行一次校正就能够消除碰撞前车速误差。研究结果证明该模型和算法具有极好的稳定性和收敛性。

碰撞前车速；碰撞后车速；误差

Keywords:pre-crash speed； post-crash speed；error

前言

在汽车碰撞事故分析中，准确计算碰撞前车速至关重要。汽车碰撞事故分析有多种方法，其中基于动量守恒定律的典型汽车碰撞模型(以下简称模型)被广泛用于计算碰撞前车速[1]。通常采用反推算法(以下简称反推法)计算碰撞前车速，即根据现场勘查数据，应用动能定理和运动学公式计算碰撞后车速，然后将其代入模型计算碰撞前车速[2-3]。实用中发现，应用动能定理和运动学公式计算的碰撞后车速有时不符合实际情况。因此，应用模型计算的碰撞前车速难免也存在误差。尽管有些学者研究了模型中主要参数误差对碰撞前车速的影响规律[4-5]，但是鉴于碰撞后车辆运动的复杂状态，应用动能定理和运动学公式难以准确计算碰撞后车速。国外多利用已开发的事故分析软件和配套的事故车辆与现场参数数据库，通过模拟迭代的正推算法计算出与停车位置吻合的碰撞前车速[6-8]，并不断对数据库进行更新。目前国内进行的相关研究甚少，缺乏完整的事故车辆和现场参数数据库，故多根据实际经验对模型计算的碰撞前车速误差进行调整[9]，这种方法速度慢且准确性难以保证。为对汽车碰撞事故做出准确的分析，剔除实用中模型存在的瑕疵，对碰撞前车速误差进行校正的研究具有重要的意义。

1 模型

模型基于切向和法向坐标系建立。以车辆2(被撞车辆)的质心垂直被撞面向外为n轴(法向坐标轴)，n轴逆时针旋转90°为τ轴(切向坐标轴)。为统一车速和车辆转动角速度的方向，在车辆1和车辆2的质心上建立坐标轴方向相同的切向和法向坐标系，即τicini坐标系(下标i＝1，2表示车辆1和车辆2)。应用动量守恒定律和碰撞中心弹性变形条件，文献[10]中建立的模型为

式中:A0和A分别为碰撞前车速系数矩阵和碰撞后车速系数矩阵；v0和v分别为碰撞前车速矩阵和碰撞后车速矩阵(以下简称碰撞前和碰撞后车速)。v0＝(v10n，v10τ，v20n，v20τ，ω10，ω20)T和 v＝ (v1n，v1τ，v2n，v2τ，ω1，ω2)T，其中:vi0n和 vi0τ分别为碰撞前车速的法向和切向分量；i＝1，2表示车辆 1和车辆 2；ωi0为碰撞前车辆的横摆角速度(以下简称碰撞前角速度)；vin和viτ分别为碰撞后车速的法向和切向分量；ωi为碰撞后角速度。

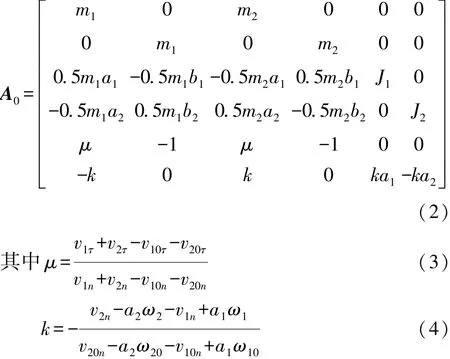
式中:mi为车辆质量；ai和bi分别为碰撞中心的切向坐标和法向坐标(简称切向坐标和法向坐标)；Ji为车辆过质心绕垂向轴的转动惯量；μ和k分别为碰撞中心切法比和弹性恢复系数(二者皆为力学参数)。 将 A0中第 6 行元素依次用 1，0，-1，0，-a1，a2替代后得到A。

2 算法与误差

反推法就是先根据事故车辆损坏情况估算μ和k，再根据事故现场勘查数据计算碰撞后车速v，最后应用模型计算碰撞前车速v0的计算过程。应用动能定理公式和运动学公式计算的v和根据事故车辆损坏情况估算的μ和k难免存在误差，而用车辆碰撞试验结果检验反推法计算的碰撞前车速是研究误差原因的有效方法。用于研究碰撞前车速误差原因的2起车辆碰撞试验现场分别如图1和图2所示。试验数据[11-12]列于表1。

图1 试验I现场简图

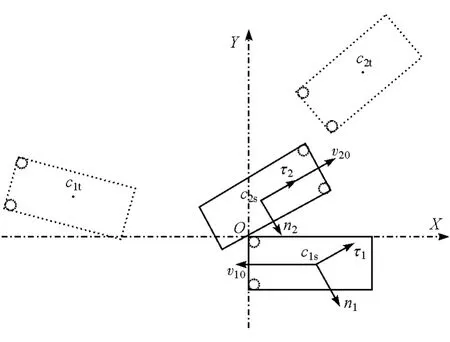
图2 试验II现场简图

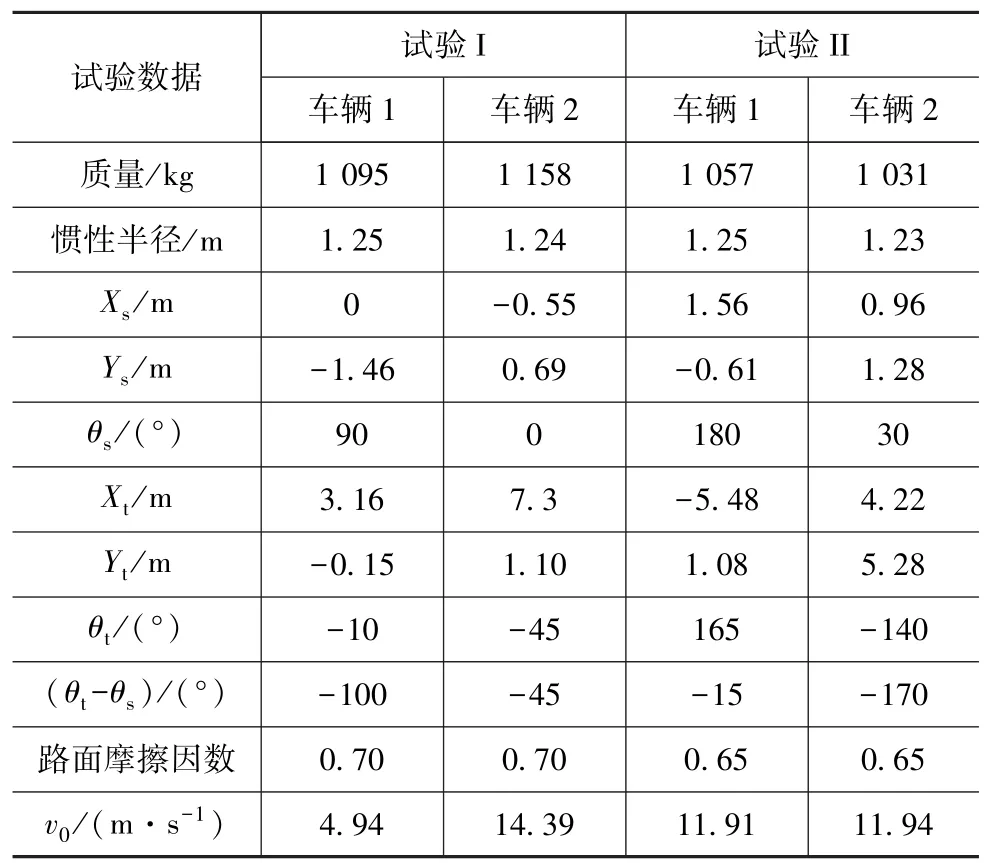
表1 试验数据

表1中:X和Y为车辆质心在地面坐标系(XOY坐标系)中的坐标值；θ为车辆纵轴与X轴正向的夹角(逆时针为正)；下标s为碰撞接触瞬间的值；下标t为停车位置的值。

(1)计算碰撞后车速

根据试验现场简图(图1和图2)，碰撞后车辆的滑行距离si和滑行方向角γi为

式中:si和γi为碰撞后车辆的滑行距离和滑行方向角(与X 轴逆时针的夹角为正)；(Xis，Yis)和(Xit，Yit)分别为碰撞接触瞬间和停车位置车辆质心在XOY坐标系中的坐标值。

应用动量定理和运动学公式推导出的碰撞后车速计算公式为

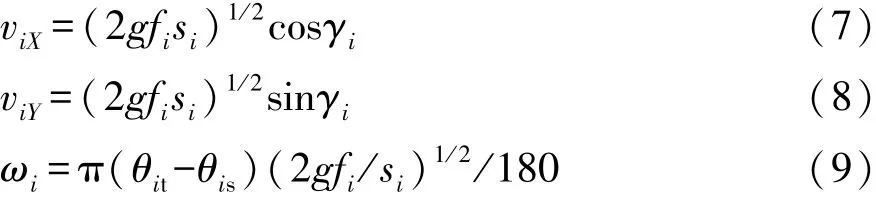
式中:viX和viY为碰撞后车速的X轴和Y轴分量；g为重力加速度；fi为路面摩擦因数；ωi为碰撞后角速度；θit和θis为碰撞后停车位置车辆方向角和碰撞前车速方向角；(θit-θis)为车辆转角。

以O点(碰撞中心)为原点的XOY坐标系和以车辆质心为原点的τcn坐标系之间可以进行坐标转换[13]。转换至τcn坐标系后的坐标值和车速值列于表2。

表2 转换后的坐标值和车速值

根据表2，由式(3)和式(4)计算得到试验I时μI＝1.301217039 和 kI＝-0.536883603。

(2)计算碰撞前车速

根据表 1、表 2，μI和 kI，由式(2)得到 A0和 A。将A0，A和表 2中碰撞后车速 v＝(-2.6235，6.3285，-0.5417，10.3709，-3.4936，-1.0371)T代入式(1)中，计算得到 v0＝(-3.8751，4.6999，0.6418，11.9109，-1.9719，-0.7694)T。 将 v0与表 2中试验 I的结果 v0T＝(-4.94，0，0，14.39，0，0)T(准确值)进行对比，发现v0存在较大误差。

3 误差的原因和校正

根据反推法的计算过程，v，μ和k是导致v0存在误差的因素。根据式(3)和式(4)，v和μ，k分别有6个和4个影响分量。为此，以试验I为例，先以对 v 进行校正。 将 A0，A 和 v0T＝(-4.94，0，0，14.39，0，0)T代入式(1)中，计算得到 v＝(-3.6884，1.6286，-1.1835，12.85，-1.5217，-0.2677)T(校正)。将 v(校正)代入式(1)，计算得到 v0＝(-4.9399，0.0001，-0.0001，14.3899，0，0)T(校正)。计算结果表明:v的误差是影响v0准确性的关键因素。

将 v0T＝(-4.94，0，0，14.39，0，0)T和 v(校正)代入式(3)和式(4)，计算得到μ＝1.3010279(校正)和 k＝-0.536869433(校正)。 根据表 1、表 2，μ(校正)和 k(校正)，由式(2)得到 A0(校正)和 A(校正)。

将A0(校正)，A(校正)和v(校正)代入式(1)，计算得到 v0＝ (-4.94，0.0003，0，-14.3897，-0.0002，-0.0001)T(校正)。结果表明:对μ和k校正后，碰撞前车速反而偏离准确值。因此，应分别对μ 或 k校正。 根据表1、表 2，μ(校正)和 kI，由式(2)得到A0(部分校正)和A(部分校正)。将A0(部分校正)，A(部分校正)和v(校正)代入式(1)，计算得到 v0＝ (-4.9399，0.0004，-0.0001，-14.3897，-0.0003，-0.0001)T(部分校正)。对μ或k进行3种校正后的计算结果列于表3。

由表3可知:力学参数误差对碰撞前车速准确性的影响极小；而碰撞后车速误差对碰撞前车速准确性的影响起决定性作用。

同理，以试验II的结果为准确值进行反推法碰撞前车速误差校正后的计算结果列于表4。

对比表3和表4可知:(1)试验I对v进行校正后，碰撞前车速中误差最大值仅为0.000 4(校正③)，可见力学参数误差对碰撞前车速准确性的影响很小，因此，碰撞后车速误差对碰撞前车速准确性的影响起决定性作用；(2)试验II的校正①～校正④，碰撞前车速误差更小，说明试验II受力学参数误差的影响更小；(3)在表3和表4中，校正④效果最好，表明在消除碰撞前车速误差的过程中对k的误差校正作用更明显。

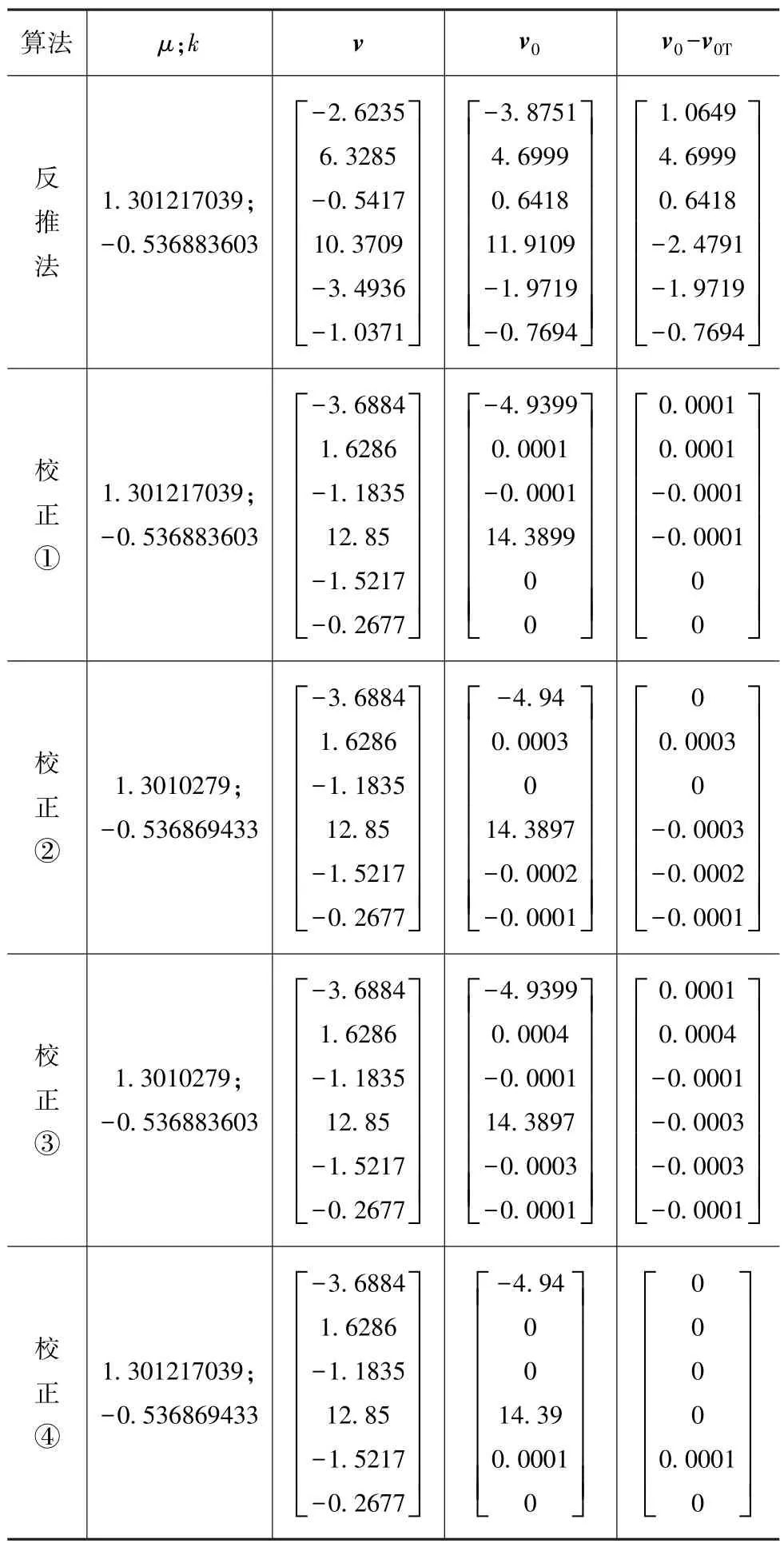
表3 误差校正结果I

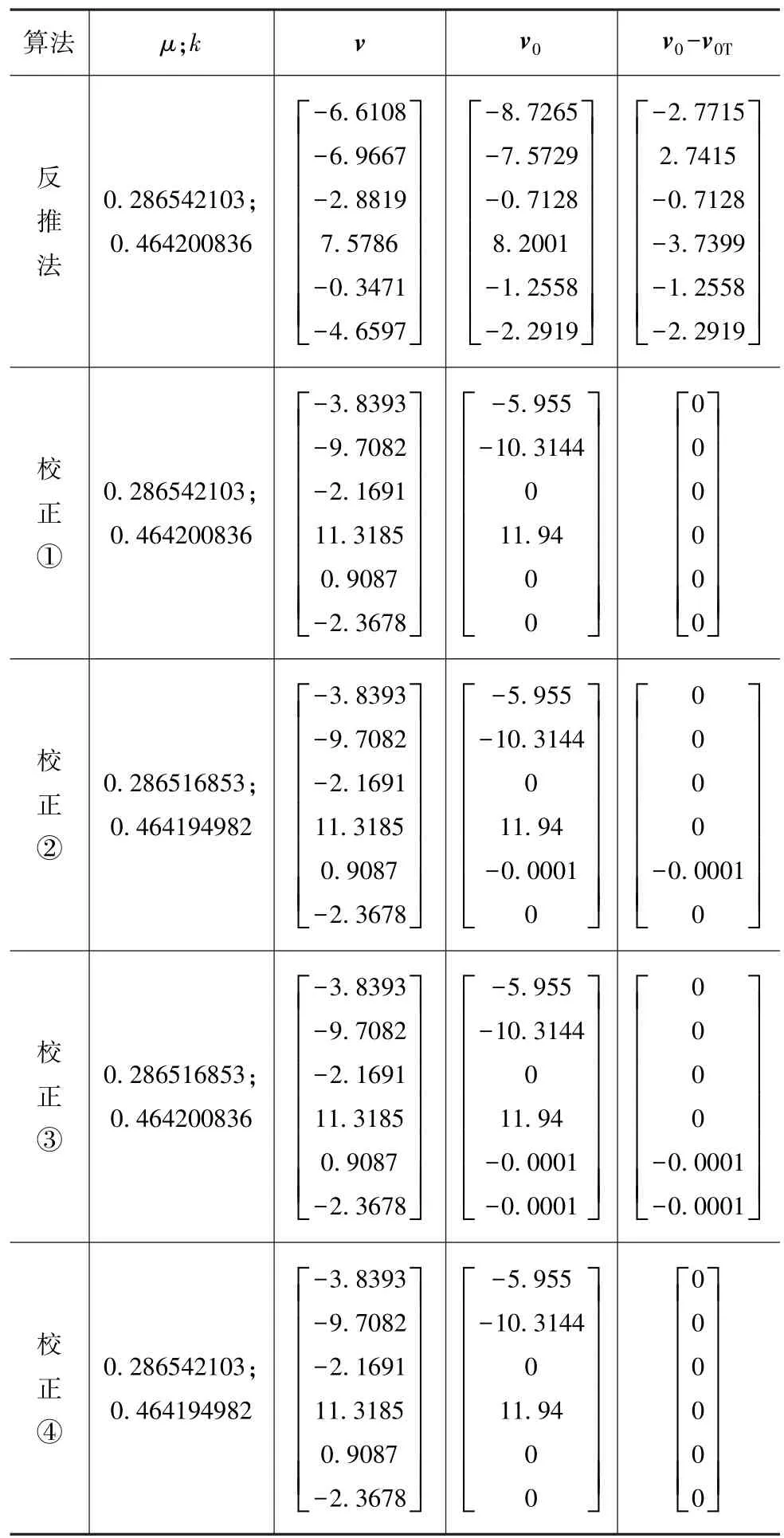
表4 误差校正结果II

对比图1和图2，试验I和试验II在碰撞情况上的主要差别在于:碰撞位置与角度和碰撞前、后的车速不同。这些差别对力学参数产生直接的影响，为此，建立如下分析指标:式中:Eμ为碰撞中心切法比的相对误差；μ为碰撞中心切法比的估算值；μA为碰撞中心切法比的校正值；Ek为弹性恢复系数的相对误差；k为弹性恢复系数的估算值；kA为弹性恢复系数的校正值。

根据表5，对比分析指标Eμ和Ek，试验I均大于试验II。结果表明，试验II受力学参数误差的影响更小，因此，更易于彻底消除碰撞前车速误差。

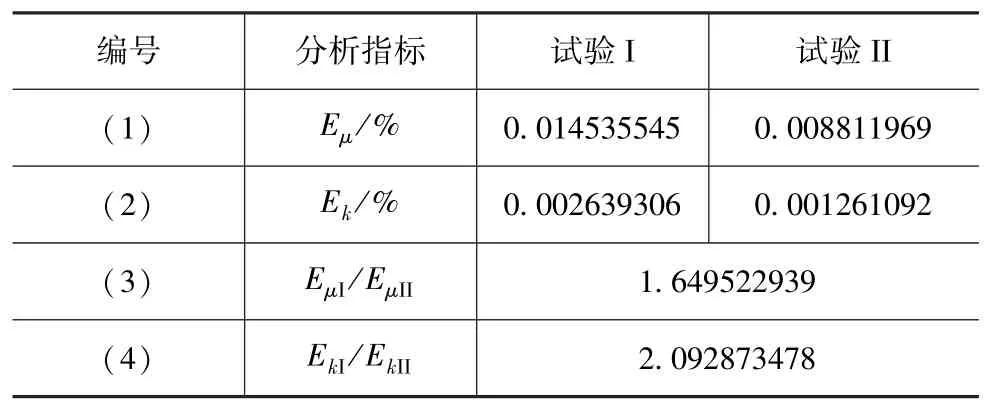
表5 力学参数影响分析指标

4 结论

以2起车辆碰撞试验结果为准确值对模型反推法计算的碰撞前车速误差进行了校正研究。结果表明:碰撞后车速误差是导致碰撞前车速误差的决定性原因，而相对而言力学参数误差的影响则小得多。对碰撞试验模拟计算的结果表明，只需对碰撞后车速误差和力学参数误差进行一次校正即可得到准确的计算结果，从而证明模型和算法具有极好的稳定性和收敛性。对车辆碰撞情况的研究表明力学参数相对误差越小越易于彻底消除碰撞前车速误差。研究成果提供了一种简单有效的碰撞前车速误差校正方法；确立了彻底消除碰撞前车速误差的研究目标。

[1] 郝洪涛，余志远，滕飞.基于VB的典型交通事故形态车辆行驶速度鉴定[J].农业装备技术，2010，36(3):54-55.

[2] 张健，张鑫，李江，等.典型汽车碰撞模型自选参数的敏感性分析[J].汽车工程，2012，34(10):905-908.

[3] 刘志强，汪澎，张建华.斜碰撞再现反推算法研究[J].公路交通科技，2009，26(1):144-148.

[4] 张健，张鑫，梁超，等.车辆转动惯量估算误差对碰撞前车速估算值的影响[J].汽车工程，2015，37(2):175-178.

[5] 张健，张鑫.汽车碰撞模型中力学参数误差对碰撞前车速的影响[J].西南交通大学学报，2011，46(2):259-263.

[6] NEADE J，SMITH R.The determination of vehicle speeds from delta-V in two vehicle planar collisions[J].Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering，2011，225(1):43-53.

[7] LIU Chunke， SONG Xinping， WANG Jiao.Simulation analysis of car front collision based on LS-DYNA and hyper works[J].Journal of Transportation Technologies，2014，4(4):337-342.

[8] PRENTKOVSKISO，SOKOLOVSKIJE，BARTULISV.Investigating traffic accident:a collision of two motor vehicles[J].Transport，2010，25(2):105-115.

[9] 李江，张大强，吴建平，等.事故再现中对速度计算结果的调整[J].公路交通科技，2003，20(2):104-107.

[10] 李江.交通事故力学[M].北京:机械工业出版社，2004.

[11] 魏朗，陈荫三，石川，等.车辆碰撞过程的试验分析研究[J].汽车工程，2000，22(4):256-261.

[12] 魏朗，郭应时，余强.车辆实车碰撞试验的模拟再现[J].西安公路交通大学学报，2000，20(1):88-91.

[13] 张建.汽车碰撞事故模型病态性处理方法的研究[D].长春:吉林大学，2007.

Correction of Pre-crash Speed Error Based on Test Results

Zhang Jian1， Liang Chao1， Gao Jingui1， Ding Tongqiang2＆ Li Jiang2
1.College of Automible and Civil Engineering， Beihua University， Jilin 132013； 2.College of Transportation， Jilin University， Changchun 130022

To control pre-crash speed error calculated with typical vehicle collision model，reverse derivation algorithm is adopted，with test and simulation on pre-crash speed conducted.The results of simulation show that post-crash speed error is the key factor affecting pre-crash speed error，while the effects of mechanics parameters are relatively insignificant.With the crash test results taken as reference base，a study is performed on the different corrections on the errors of pre-crash speed simulated.The results show that pre-crash speed error can be eliminated by just one correction on post-impact speed error and mechanics parameter error，demonstrating the good stability and convergence property of the model built and the algorithm adopted.

10.19562/j.chinasae.qcgc.2017.09.008

∗国家自然科学基金(51178001和31570556)和吉林市科技发展计划项目(20090404)资助。

原稿收到日期为2016年6月3日。

张健，教授，E-mail:zhjdp＠126.com。