激发猜测动机 引导科学探究

吴进

【摘 要】猜测是数学教学中一种重要的思维方法，是创新、创造的前奏。文章以“钉子板上的多边形”一课的教学为例，尝试运用猜测的教学方法，让学生在活动、比较、推理中猜测，激发学生的学习热情和探究兴趣，促进了学生创新思维能力的培养。

【关键词】 数学教学；探讨；推理

中图分类号：G623.5 文献标识码：A 文章编号：1671-0568（2017）24-0089-02

数学家G·波利亚说过，在数学领域中猜想是合理的、值得尊重的，是负责任的态度。引导学生积极地猜测是对科学探究的指引，符合小学生的认知发展水平，这样不仅能让学生获得知识、掌握科学探究的有效方法，而且培养了他们的创新思维能力。“钉子板上的多边形”是一节综合实践活动课，需要在老师的指导下，引导学生自主探究，自主地进行综合性学习，而探究的源头就是猜测。所以，笔者在教学“钉子板上的多边形”这一课时，进行了以下几个方面的猜测：

一、在操作活动中猜测，激发主动探究的欲望

苏霍姆林斯基说过，在人的心灵深处，都有一种根深蒂固的需要，就是希望自己是一个发现者、研究者、探索者。而在儿童的精神世界中，这种需要特别强烈。所以猜想能使学生带着一种无比高涨的激励的情绪从事学习和思考，让他们能够释放出自身的生命潜能，带着自信、欲望探求数学规律。

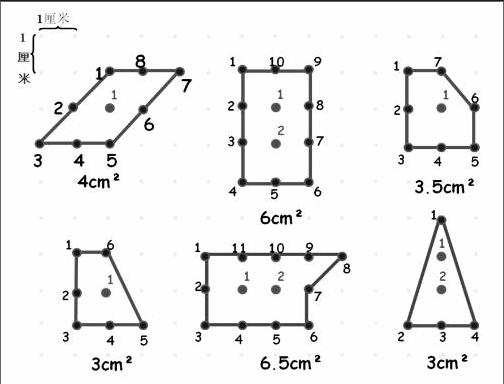
在探究过程中，如果让学生动手操作，并让学生仔细地观察，对活动的结果进行大胆的猜测，那么，猜测将以它独特的魅力扣住学生的心弦，使其热情饱满、思维活跃，融入良好的学习氛围中，进而步入学习的最佳境地。所以在教学一开始，笔者就先让学生动手在钉子板上围一围各种不同的多边形，说说它们的面积是多少，再在点子图上出示所围的多边形及其面积：

笔者提问：“猜一猜，你觉得这些多边形面积会跟什么有关呢？”激发了学生探究的兴趣，他们积极地思考、猜测：可能跟多边形内的小方形个数有关、可能跟每两个钉子之间的距离有关、可能跟钉子板上的钉子数有关……笔者适时提问：“既然你们觉得钉子板上多边形的面积和钉子数有关，那会和哪些钉子有关呢？”并请同学上来摸一摸，引发进一步的猜测。这样让学生从多角度的思考中，明确了本节课的学习内容是围绕“钉子板上多边形的面积与其边上钉子数、内部钉子数之间的关系”，从而对接下来学习新的知识充满期待，产生强烈的学习欲望。

二、在观察比较中猜测，掌握自主探究的方法

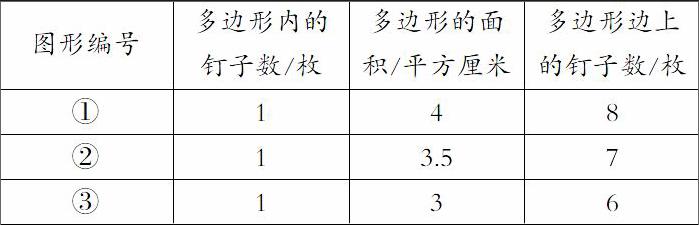
牛顿说过，没有大胆的猜想，就做不出伟大的发现。因此，教师要鼓励学生大胆猜想，经历观察、比较、猜测，再观察、再比较、再猜测的过程，让学生在探究性学习中不断迸发出思维的火花，让學生学习的自主性得到充分体现、合作探究能力得到充分提升。在教学“钉子板上的多边形”中，为了便于观察，笔者指导学生，将操作所得的数据整理成表格，接着出示一张表格：

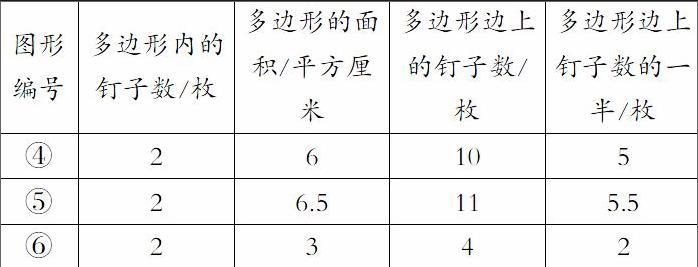
让学生仔细观察这张表格，比较表格中的数据，同学们初步发现了：当多边形内只有1枚钉子时，钉子板上多边形的面积是它边上钉子数的一半。继而出示第二张表格：

学生进一步发现：当多边形内有2枚钉子时，多边形的面积是它边上钉子数的一半加1。这两条规律是由表格中特定的数据得到的，此时学生就会产生强烈的疑问：“是不是所有符合条件的多边形都满足这个规律呢？”这样使学生带着强烈的好奇心、求知欲，和同学合作探究，用例证的方法证明自己的猜想，真正从观察、比较、猜测、证明中，探索其内在的数学规律。

三、在合情推理中猜测，培养科学探究的思维

1. 类比推理

数学教育家G·波利亚指出，学生自己提出了猜想，也就会有追求证明的渴望，因而此时的数学教学最富有吸引力，切莫错过时机。在教学中，笔者鼓励学生在已有知识经验的基础上，和同学积极讨论交流，大胆地深入猜想，并运用类比推理，得出具有共性的数学规律，从而极大地培养了学生发现问题、解决问题的能力。

比如，学生已经发现了“当b=1时，S=n÷2+0；当b=2时，S=n÷2+1”，但他们并不满足于现状，继而会自己提出：“还可以研究内部有3枚、4枚、5枚……钉子的多边形。”在初步掌握已有规律的前提下，学生自然而然地可以类比猜测出：当b=3时，S=n÷2+2；当b=4时，S=n÷2+3……这样的“猜测”。

实践证明：从学生已有发现的基础上进行猜测，给了学生质疑的机会，让他们自己选择合适图形，用例证法对推测出的规律与同学进行讨论、类比推理，对猜测的合理性进行判断，从而培养了他们自主探究数学规律的能力。

2. 归纳推理

从已知特殊规律出发的类比推理，让规律的本质得以体现，那么进一步的归纳推理不仅能发现其一般规律，更能发展学生的理性思维能力，也是科学探究数学规律所必备的。

在“钉子板上的多边形”教学过程中，学生已经发现一些“多边形内部的钉子数与多边形的面积之间特殊的关系”。在此基础上，笔者引导学生猜想：“右边的式子有什么是一样的？什么变了？怎么变？”学生在观察猜测中、在老师的引导下进行归纳推理，感受这些式子的本质属性：①都有内部是1枚钉子数的多边形面积。②加数是多边形内部钉子数减1。最后，笔者引导学生发现、明确“计算钉子板上多边形面积”的一般规律：可以先算出内部有1枚钉子数的多边形面积，再加上b-1就可以算出内部有b枚钉子数的多边形面积，也就是当多边形内有b枚钉子数时，S=n÷2+（b-1）。

辩证唯物主义强调的是从特殊到一般，数学规律的发现也是如此。在特定的情境中，学生猜测、观察、比较、验证时，会发现很多特殊的数学规律。但是这些特殊的规律，只有在被归纳推理成一般规律时，才能被发现其本质属性，才能大放异彩，从而促进学生理性数学思维的发展。

总之，猜测是数学教学中一个引之有效的方法。笔者在教学“钉子板上的多边形”一课时，用猜测点燃学生对知识的渴求之火，激发了学生的思维之花，恰到好处地进行比较、证明，从类比推理到归纳推理，一步一步地让学生的科学探究达到了高潮，培养了学生的数学思维能力，从而提高教学效率。

参考文献：

[1] 张顺仪.让学生在猜测中学习数学[J].东方青年·教师，2013，（18）.

[2] 尚新芝.浅谈数学教学中的特殊和一般[J].试题与研究：新课程论坛，2009（23）：37-37.

（编辑：杨 迪）endprint